Fast Assessment of Wildﬁre Spatial Hazard with GPGPU

Donato D’Ambrosio

, Salvatore Di Gregorio

, Giuseppe Filippone

, Rocco Rongo

William Spataro

and Giuseppe A. Trunﬁo

Department of Mathematics, University of Calabria, 87036 Rende, CS, Italy

Department of Earth Sciences, University of Calabria, 87036 Rende, CS, Italy

Department of Architecture, Planning and Design, University of Sassari, 07041 Alghero, SS, Italy

Keywords:

GPGPU, Cellular Automata, Wildﬁre Simulation, Wildﬁre Susceptibility, Hazard Maps.

Abstract:

In the ﬁeld of wildﬁre risk management the so-called burn probability maps (BPMs) are increasingly used

with the aim of estimating the probability of each point of a landscape to be burned under certain environ-

mental conditions. Such BPMs are computed through the explicit simulation of thousands of ﬁres using

fast and accurate simulation models. However, even adopting the most optimized simulation algorithms, the

building of simulation-based BPMs for large areas results in a highly intensive computational process that

makes mandatory the use of high performance computing. In this paper, General-Purpose Computation with

Graphics Processing Units (GPGPU) is applied, in conjunction with a speciﬁcally devised wildﬁre simulation

model, to the process of BPM building. Using two different GPGPU devices, the paper illustrates two different

implementation strategies and discusses some numerical results obtained on a real landscape.

1 INTRODUCTION

Systematic risk-assessment procedures are increas-

ingly considered as important components of the mul-

tifaceted strategy for mitigating the harmful impact

of wildﬁres. Among the different tools to support

ﬁre hazard management, there are the so-called burn

probability maps (BPMs), which attempt to provide

an estimate of the probability of a point in a land-

scape to be burned under certain environmental con-

ditions. Since the many factors that determine the ﬁre

behaviour interact nonlinearly to determine the haz-

ard level, models for simulating wildﬁre spread are

increasingly being used to build BPMs (Carmel et al.,

2009; Ager and Finney, 2009). In particular, the typ-

ical approach is based on carrying out a high number

of simulations (e.g. many thousands), under differ-

ent weather scenarios and ignition locations (Carmel

et al., 2009).

In order to obtain reliable results in reasonable

time, such an approach must be based on fast and

accurate simulation models operating on high-quality

high-resolution remote sensing data (e.g., Digital El-

evation Models, vegetation description, etc.). Among

the different wildﬁre simulation techniques (Sulli-

van, 2009), those based on Cellular Automata (CA)

(Kourtz and O’Regan, 1971; Lopes et al., 2002; Trun-

ﬁo, 2004; Yassemi et al., 2008; Peterson et al., 2009)

represent an ideal approach to build a BPM. This

is because they provide accurate results and can of-

ten perform the same simulations in a fraction of the

run time taken by different methods (Peterson et al.,

2009).

However, because of the required high number of

explicit ﬁre propagations, even using the most op-

timized algorithm, the building of simulation-based

BPMs often results in a highly intensive computa-

tional process. This is particularly true when the BPM

concerns a large area. For example, building a high-

resolution BPM covering a regional territory can be

often infeasible using standard computing facilities.

In the latest years, while the computational

needs of such sophisticated risk-assessment proce-

dures have been increasing, the same happened to the

availability of high-performance computers. A vari-

ety of parallel computing systems are available to-

day, including massive parallel computers, clusters,

computational grids, multi-core CPU computers and

the recently emerging General-Purpose computing on

Graphics Processing Units (GPGPU), in which multi-

core Graphics Processing Units (GPU) perform com-

putations traditionally carried out by the CPU.

In this paper, GPGPU is applied, in conjunction

with a wildﬁre simulation model, to the process of

260

D’Ambrosio D., Di Gregorio S., Filippone G., Rongo R., Spataro W. and A. Trunﬁo G..

Fast Assessment of Wildﬁre Spatial Hazard with GPGPU.

DOI: 10.5220/0004070902600269

In Proceedings of the 2nd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2012),

pages 260-269

ISBN: 978-989-8565-20-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

BPM computation. In particular, the proposed ap-

proach is based on a CA simulation approach which

represents a suitable tradeoff between accuracy and

speed of execution. The adopted parallel computation

consists of the iterative simultaneous simulation of a

number of wildﬁres with GPGPU, in order to cover

the whole area under study. The paper illustrates two

different implementation strategies in terms of model

parallelisation, which correspond to different perfor-

mances in terms of computing time. In addition, using

two different GPGPU devices some numerical results

obtained on a real Mediterranean landscape, which is

historically characterized by a high incidence of wild-

ﬁres, are discussed.

The paper is organized as follows. The next sec-

tion outlines the main characteristics of the adopted

CA simulation model and illustrates some details of

the typical approach for BPM computation. Then, in

section 3 some introductory elements of the adopted

GPGPU approach are presented. Section 4 outlines

the proposed parallel approaches and in section 5

some of their computational characteristics are empir-

ically investigated. The paper ends with section 6 in

which we draw some conclusions and outline possible

future work.

2 A CA FOR FAST WILDFIRE

SIMULATION AND SPATIAL

HAZARD ASSESSMENT

As most wildﬁre spread simulators, the approach

adopted in this paper is based on the Rothermel ﬁre

model (Rothermel, 1972; Rothermel, 1983), which

provides the heading rate and direction of spread

given the local landscape and wind characteristics.

An additional constituent is the commonly assumed

elliptical description of the spread under homoge-

neous conditions (i.e. spatially and temporally con-

stant fuels, wind and topography) (Alexander, 1985).

Under the above hypothesis, given the assumption of

homogeneity at the cell level, the CA transition func-

tion uses the elliptical model for producing the com-

plex patterns that correspond to the ﬁre spread in het-

erogeneous conditions.

As mentioned above, CA methods for simulating

wildﬁre can be highly optimized from the computa-

tional point of view. For this reason they are well

suited for the process of building BPMs. Neverthe-

less, a well-known problem associated with the cell-

based methods is the distortion that may affect the

produced ﬁre shape. For example, as shown later

in Section 2.1, under homogeneous conditions and in

presence of wind, the shape of the heading portion of

the ﬁre is often angular rather than rounded as in the

expected ellipse (French et al., 1990). Unfortunately,

such systematic errors under homogeneous conditions

typically correspond to inaccurate results also in real

applications (Cui and Perera, 2008; Peterson et al.,

2009) and in thus in the computation of BPMs.

Several studies have recognized that the distorted

shapes are caused by the ﬁre only being able to prop-

agate along the small number of ﬁxed directions im-

posed by the raster (French et al., 1990; Johnston

et al., 2008; Peterson et al., 2009).

The CA-based method adopted in this paper pro-

vides a satisfactory level of accuracy thanks to some

of the ideas already presented in the literature, namely

extending the size of the neighbourhood (O’Regan

et al., 1976; French et al., 1990) and avoiding centre-

to-centre ignitions between cells (Johnston et al.,

2008; Trunﬁo et al., 2011). However, instead of using

a random irregular grid as in (Johnston et al., 2008),

here the randomization is explicitly introduced over

the regular lattice according to the approach proposed

by (Miyamoto and Sasaki, 1997) for simulating lava

ﬂows through CA. Moreover, the run time efﬁciency

of the model is signiﬁcantly high thanks to an adap-

tive time step strategy (Peterson et al., 2009), which

simulates the progression of the ﬁre by avoiding un-

necessary computation.

2.1 Model Description

As in different CA-based wildﬁre simulation mod-

els (Trunﬁo, 2004; Peterson et al., 2009), the two-

dimensional ﬁre propagation is simulated through a

growing ellipse having the semi-major axis along the

direction of maximum spread, the eccentricity related

to the intensity of the so-called effective wind and one

focus acting as a ‘ﬁre source’.

At each time step the ellipse’s size is incremented

according to both the duration of the time step and

maximum rate of spread (see Figure 1). Afterwards,

a neighbouring cell invaded by the growing ellipse is

considered a candidate to be ignited by the spreading

ﬁre. In case of ignition, a new ellipse is generated

according to the amount of overlapping between the

invading ellipse and the ignited cell.

More formally, the model is a two-dimensional

CA with square cells deﬁned as:

CA = hK , N , S, P , ω, Ψi (1)

where:

– K is the set of points in the ﬁnite region where

the phenomenon evolves. Each point represents

the centre of a square cell;

FastAssessmentofWildfireSpatialHazardwithGPGPU

261

Figure 1: Growth of the ellipse γ locally representing the

ﬁre front. The symbol ρ denotes the forward spread which

is incremented by ∆ρ at the i-th time step.

– Q is a set of random local sources (RLSs), one

point for each cell; they are randomly generated at

the beginning of the simulation within an assigned

radius δ from each of the centres in K , as shown

in Figure 2. As detailed later, a new ignition in a

cell consists of a new ellipse having its rear focus

on the local source q ∈ Q ;

– N is the set that identiﬁes the pattern of cells in-

ﬂuencing the cell state change (i.e the neighbour-

hood);

– S is the ﬁnite set of the states of the cell, deﬁned

as the Cartesian product of the sets of deﬁnition

of all the cell’s substates;

– P is the ﬁnite set of global parameters which de-

ﬁne the fuel bed characteristics according to the

standard fuel models used in BEHAVE (Andrews,

1986);

– ω : S

|N |

→ S is the transition function accounting

for the ﬁre ignition, spread and extinction mecha-

nisms;

– Ψ is the set of global functions, activated at each

step before the application of the transition func-

tion ω to modify either the values of model param-

eters in P or the cells’ substates. Among these,

the function φ

adapts the size p

∆t

of the time step

according to both the size of the cells p

and cur-

rent maximum spread rate in the whole automa-

ton. The value of p

∆t

is then used by another func-

tion, φ

, for keeping the current time up to date.

The cell’s substates include all the local quantities

used by the transition function for modelling the inter-

actions between cells (i.e. ﬁre propagation to neigh-

bouring cells) as well as its internal dynamics (i.e. ﬁre

ignition and growth). In particular, the relevant com-

ponents of the state of each cell are:

– the altitude z ∈ R;

Figure 2: An example of RLSs arrangement in a subset

of the automaton. Each RLS occupies a random position

within a distance δ from the cell centre.

– the fuel model µ ∈ N, which is an index referring

to one of the mentioned fuel models that spec-

iﬁes the characteristics of vegetation relevant to

Rothermel’s equations;

– the combustion state σ ∈ S

, which takes one of

the values unburnable, not ignited, ignited and

burnt.

– the accumulated forward spread ρ ∈ R

≥0

, that is

the current distance between the focus f of the lo-

cal ellipse and the farthest point on the semi-major

axis (see Figure 1);

– the angle θ ∈ R (see Figure 1), giving the direc-

tion of the maximum rate of spread. In the con-

text of the semi-empirical Rothermel’s approach,

such an angle is obtained through the composition

of two vectors, namely the so-called wind effect

and slope effect (Rothermel, 1972), both obtained

on the basis of the local wind vector, local terrain

slope and fuel model;

– the maximum rate of spread r ∈ R

≥0

, also pro-

vided by Rothermel’s equations on the basis of the

relevant local characteristics (Rothermel, 1972);

– the eccentricity ε ∈ [0, 1] of the ellipse γ represent-

ing the local ﬁre front, which is obtained as a func-

tion of both the wind and terrain slope through the

empirical relation proposed in (Anderson, 1983).

Among the remaining substates are the local wind

vector and the relative humidity value of the cell, both

provided as external input to the model.

As mentioned above, the CA model is based on

an extended Moore’s neighbourhood composed of 24

cells. Also, as explained below and represented in

Figure 2, the use of RLSs inside each cell allows for

obtaining a high number of different spread direction

during the ﬁre propagation in the landscape, thus sig-

niﬁcantly improving the accuracy of the results.

SIMULTECH2012-2ndInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

262

The transition function ω concerns only cells that

are in the burning state. The ﬁrst step of ω consists

of checking the condition that triggers the transition

to the burnt state. The latter is veriﬁed when all the

neighbouring cells are in either the ignited or in the

unburnable state, that is when the cell’s contribution

is no longer necessary to the ﬁre spread mechanism.

Then, if the cell still belongs to the ﬁre front, ω

updates the size of the local ellipse γ. This is accom-

plished by adding to the accumulated forward spread

ρ the product of the rate of spread r and the step size

∆t. The latter is dynamically established by the global

function φ

according to the procedure proposed by

(Peterson et al., 2009).

The next step of ω consists of testing if the ﬁre is

spreading towards other cells c

of the neighbourhood

that are in the not ignited state. Since in the current

cell the ﬁre front is represented by a local ellipse γ,

such a spread test is carried out through checking if γ

includes the RLS q

of the cell c

(see Figure 3). To

this purpose the current spread in direction q

can be

easily computed using the mathematical properties of

the ellipse.

Figure 3: The i-th neighbouring cell intersected by the el-

lipse γ locally representing the ﬁre front.

If q

is inside γ, then a new ellipse γ

is generated

for the cell c

, having the following characteristics:

• both the intensity r

of the maximum spread rate

vector and its inclination θ

are computed through

the proper Rothermel’s equations (Rothermel,

1972);

• the eccentricity ε

is determined using the empiri-

cal formula proposed by (Anderson, 1983), which

accounts for both the effect of wind and topog-

raphy through the previously mentioned effective

wind speed (McAlpine et al., 1991).

• as shown in Figure 3, its size is initialized so that

its most advanced point lies on the ellipse γ;

• the RLS q

is assumed as rear focus.

When compared with a typical CA algorithm for

wildﬁre simulation, the main advantage of the ap-

proach based on the RLSs, lies in its ability to in-

crease the directions of spread. This leads to an im-

proved accuracy as shown in Figure 4, where the ex-

pected ﬁre shape under homogeneous conditions is

compared with the simulated shapes given by differ-

ent CA approaches.

Figure 4: A comparison between the simulated ﬁre shapes

obtained under homogeneous condition with different CA

approaches: a) standard CA based on the Moore’s neigh-

bourhood and on a centre-to-centre ignition scheme; b) CA

based on an extended neighbourhood composed of 24 cells

with a centre-to-centre ignition scheme; c) CA based on the

same neighbourhood used in b) together with the RLSs. The

continuous line represents the expected shape.

2.2 A Simulation-based Approach for

Building BPMs

In the latest years, the use of hazard maps based on

the explicit simulation of natural phenomena has been

increasingly investigated as an effective and reliable

tool for supporting risk management (Rongo et al.,

2008; Carmel et al., 2009; Ager and Finney, 2009;

Rongo et al., 2011).

In the case of wildﬁre, the most general approach

for computing a BPM on a landscape (Carmel et al.,

2009; Ager and Finney, 2009) consists of a Monte

Carlo approach in which a high number of different

ﬁre spread simulations are carried out, sampling from

suitable statistical distributions the random variables

relevant to the ﬁre behaviour. For example, the wind

direction for each simulated ﬁre can be sampled in a

range corresponding to the typical directions of severe

wind for the area. At the end of the process, the lo-

cal risk is computed on the basis of the frequency of

burning.

The technique for computing the BPMs adopted

in this study is based on a preﬁxed number n of

simulation runs, where each run represents a single

simulated ﬁre. The adopted weather scenario (i.e.

wind and fuel moisture content) corresponds to ex-

treme conditions for the area with regards to relevant

historical ﬁres. A regular grid of ignition locations

is adopted, which corresponds to the assumption of

a uniform ignition probability for each point of the

FastAssessmentofWildfireSpatialHazardwithGPGPU

263

landscape. Also, all the simulated ﬁres have the same

duration. The latter is selected considering the du-

ration of historical ﬁres in the regions under study.

All the other relevant characteristics are kept constant

during the simulations.

Once the latter have been carried out, the resulting

n maps of burned areas are overlaid and cells’ ﬁre fre-

quency are used for the computation of the ﬁre risk.

In particular, a burn probability p

is computed as:

f (c)

; (2)

where f (c) is the number of times the cell c is ignited

during the n simulated ﬁres. The burn probability for

a given cell is an estimate of the likelihood that a cell

will burn given a single random ignition within the

study area and given the assumed conditions in terms

of ﬁre duration fuel moisture and weather.

According to the procedure described above, the

number n of simulation runs depend on the resolution

of the grid of ignition points. In general, it is not nec-

essary to simulate a wildﬁre for each of the cells in

the automaton. In fact, considering the usual resolu-

tion of landscape data, ignitions on adjacent cells pro-

duce very similar ﬁre shapes. Nevertheless, as shown

in the application example discussed later, the number

of ﬁre simulation needed for achieving a good BPM

accuracy can be considerably high in case of study

areas with great extensions.

3 PARALLEL COMPUTING

WITH GPGPU

A natural approach to deal with the high computa-

tional effort related to construction of the BPMs, is the

use of parallel computing. Among the different paral-

lel architectures and computational paradigms, in the

last years GPGPU has attracted the interest of many

researchers (Preis, 2011; Roberts et al., 2010; Szer-

winski and G

uneysu, 2008; Filippone et al., 2011;

Pallipuram et al., 2011; Krger et al., 2010). This is

mainly due to the following reasons:

• the computational power of devices enabling

GPGPU has exceeded that of standard CPUs by

more than one order of magnitude;

• the price of a typical device for GPGPU is com-

parable to the price of a standard CPU;

• there has been a rapid increase in the programma-

bility of these devices, which has facilitated the

porting of many scientiﬁc applications leading to

relevant parallel speedups (Krger et al., 2010).

Modern GPUs are multiprocessors with a highly ef-

ﬁcient hardware-coded multi-threading support. The

key capability of a GPU unit is thus to execute thou-

sands of threads running the same function concur-

rently on different data (Single Instruction Multiple

Data archiecture). Hence, the computational power

provided by such an architecture, which can easily

reach a teraFLOP, can be fully exploited through a

ﬁne grained data-parallel approach when the same

computation can be independently carried out on dif-

ferent elements of a dataset.

The particular GPGPU platform investigated in

this paper is the one provided by nVidia, which con-

sist of a group of Streaming Multiprocessors (SMs) in

a single device. Each SM can support a limited num-

ber of co-resident concurrent threads, which share the

SM’s limited memory resources. Furthermore, each

SM consists of multiple Scalar Processor (SP) cores.

In order to program the GPU, in this paper we

use the C-language Compute Uniﬁed Device Archi-

tecture (CUDA), a programming model introduced in

2006 by nVidia Corporation for their GPUs (NVidia

corp., 2010). In a typical CUDA program, sequential

host instructions are combined with parallel GPGPU

code. The idea underlying this approach is that the

CPU organizes the computation (e.g. in terms of

data pre-processing), sends the data from the com-

puter main memory to the GPU global memory and

invokes the parallel computation on the GPU device.

After, and/or during the computation, the computed

results are copied into the main memory for post-

processing and output purposes. In some cases, the

computing scheme outlined above can be enhanced

including overlapping the CPU and GPU computation

as well as overlapping memory copying with compu-

tation (NVidia corp., 2010; NVidia corp., 2012).

In CUDA, the GPGPU activation is obtained by

writing device functions in C language, which are

called kernels. When a kernel is invoked by the CPU,

a number of threads (e.g. typically several thou-

sands) execute the kernel code in parallel on differ-

ent data. From the kernel code it is possible to dis-

tinguish the currently associated thread through some

built-in variables (i.e. threadIdx, blockIdx, and block-

Dim). This allows to select from the device mem-

ory the data to associate to that particular thread (e.g.

the cell of a CA). According to the nVidia approach

to GPGPU, threads are grouped into blocks and exe-

cuted on a SMs.

From a programmer’s point of view, it is of a cer-

tain relevance to know that the GPU can access differ-

ent types of memory. For example, a certain amount

of fast shared memory (which can be used for some

limited intra-block communication between threads)

SIMULTECH2012-2ndInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

264

can be assigned to each thread block. Also, all threads

can access a slower but larger global memory which

is on the device board but outside the computing chip.

The device global memory is slower if compared with

the shared memory, but it can deliver signiﬁcantly

(e.g. one order of magnitude) higher memory band-

width than traditional host memory (i.e. the main

computer memory). The latter is typically linked to

the GPU card through a relatively slow bus. For ex-

ample, in most hardware conﬁgurations accessing the

host memory from the GPU can be more that 20 times

slower in terms of bandwidth (i.e. Gb/s) than access-

ing the global memory. As a result, the parallel com-

putation should be organised in such a way to mini-

mize data transfers between the host and the device.

For example, in some cases it is preferable to execute

on the device code which is inefﬁcient (e.g. because

that speciﬁc part of the whole computation does not ﬁt

well with the GPGPU model of parallelism) instead

of running it on the CPU, if this allows to avoid large

amount of CPU-GPU data transfers.

4 GPGPU-BASED WILDFIRE

RISK ASSESSMENT

The CA approach is known as one of the most typical

parallel computation paradigm. In fact, the whole sys-

tem is composed of a set of independent cells, which

are inﬂuenced only by their neighbours. This allows

for: (i) computing the next state of all the cells in

parallel; (ii) accessing only the current neighbours’

states during each cell’s update, thereby giving the

chance to increase the overall efﬁciency and making

easier even the implementation on distributed mem-

ory machines. As in the sequential case, the typical

CA parallel implementation involves two memory re-

gions representing the current and next states for the

cell. For each CA step, the neighbouring values from

current are read by the transition function, which per-

forms its computation and writes the new state value

into the appropriate element of next.

In particular, the GPGPU parallel implementa-

tion of the CA illustrated above, accordingly to the

recent literature in the ﬁeld (Preis, 2011; Roberts

et al., 2010; Szerwinski and G

uneysu, 2008; Filip-

pone et al., 2011), was based on the following design

choices:

• one or more CUDA computational kernels (i.e.

threads) are assigned to each cell of the automaton

as in (Filippone et al., 2011);

• most of the automaton data (i.e. both the cur-

rent and next memory areas mentioned above)

is stored in the GPU global memory. This in-

volves: (i) initialising the current state through

a CPU-GPU memory copy operation (i.e. from

host to device global memory) before the begin-

ning of the simulation and (ii) retrieving the ﬁnal

state of the automaton at the end of the simulation

through a GPU-CPU copy operation (i.e. from de-

vice global memory to host memory). Also, at the

end of each CA step a device-to-device memory

copy operation is used to re-initialise the current

values with the next values.

In order to speed up the access to memory, the au-

tomaton data in device global memory should be or-

ganised in a way to allow coalescing access. To this

purpose, a best practice recommended by nVidia is to

use of structures of arrays rather than arrays of struc-

tures in organising the memory storage of cell’s prop-

erties (NVidia corp., 2012). Thus, while the typical

sequential implementation of the CA model described

in section 2 is based on structures or objects encapsu-

lating all the cells substates, in the GPGPU implemen-

tation it was more convenient to use simple arrays to

store the automaton. In particular, an array with the

size corresponding to the total number of cells was

allocated in the CPU memory for each of the CA sub-

states. All of such arrays were then mirrored in the

GPU together with some additional auxiliary arrays

(e.g. for storing the neighbourhood structure and the

model parameters).

A key step in the parallelisation of a sequential

code for the GPU architecture according to the CUDA

approach, consists of identifying all the sets of in-

structions that can be executed independently of each

other on different elements of a dataset (e.g., on the

different cells of the automaton). As mentioned in

Section 3, such sequences of instructions are grouped

in CUDA kernels, each transparently executed in par-

allel by the GPU threads. In particular, in the CA

model for wildﬁre simulation outlined in section 2,

two CUDA kernels have been developed:

• the kernel implementing the ﬁre propagation

mechanism (i.e. the CA transition function ω);

• the kernel for dynamically adapting the time-step

duration. Since this involves ﬁnding the minimum

of all allowed time-step sizes among the cells on

the current ﬁre front, such kernel simply imple-

ments a standard parallel reduction algorithm.

One of the critical aspects of the GPGPU imple-

mentation is related to the fact that in the whole au-

tomaton only the cells on the current ﬁre front do ac-

tual computation in the transition function. Hence,

launching one thread for each of the automaton cells

results in a certain amount of dissipation of the GPU

FastAssessmentofWildfireSpatialHazardwithGPGPU

265

computational power. For this reason, besides the

standard CA implementation (SCA) in which the

above mentioned kernels are applied to each cells of

the automaton, a more optimized CA (OCA) has also

been developed. In the OCA, the kernel that adapts

the time-step size at each iteration, also computes

the smallest rectangular bounding box (RBB) that in-

cludes any cells on the current ﬁre front, as shown

in Figure 5. Thus, the kernels implementing the CA

step are mapped only on such RBB, in this way re-

ducing the number of kernel launches and improving

signiﬁcantly the computational performance of the al-

gorithm. It is worth noting that the same strategy has

been developed for the sequential version of the pro-

gram in order to obtain a fair comparison.

Figure 5: An example of the RBB representing the envelope

of the current ﬁre front. In the OCA version, the CUDA

kernels are mapped only on the RBB.

However, notwithstanding the OCA approach,

during the simulation of a single ﬁre the RBB still

includes a number of inactive cells. For example, all

the burned cells inside the current ﬁre front are typi-

cally included in the RBB though they are not com-

putationally active. For this reason, in both the SCA

and OCA version of the algorithm, more than a sin-

gle ﬁre are simultaneously simulated. In other words,

the above mentioned kernels iterate over a number of

active ﬁres which are propagated simultaneously. Ob-

viously, such an approach requires the use of an inde-

pendent array for storing the combustion state σ of

each cell of the automaton and for each simultaneous

ﬁre. At the cost of this additional memory occupa-

tion, the approach allows for increasing the level of

device saturation with beneﬁcial effects on the com-

puting time.

Before starting the BPM construction, a pre-

processing sequential phase takes place in which for

each cell c

the maximum rate of spread r

, its direc-

tion θ

and the local ellipse eccentricity ε

(see Fig-

ure 1) are computed using the proper model equations

(Rothermel, 1972; Anderson, 1983). According to the

algorithm outlined in section 2, such pre-computed

quantities determine, together with the landscape to-

pography, the wildﬁre spread at the cell-level. Also,

during the pre-processing phase the maximum time-

step size for each cell is computed and stored in an ar-

ray in order to speed-up the time-step adaptation dur-

ing the CA iterations.

The process for the BPM computation is orga-

nized as follows. Cluster of ﬁres are iteratively simu-

lated, up to covering the entire area under study (i.e.

up to the required number n of ﬁres). In order to max-

imize the advantages of the OAC approach described

above, each cluster is composed of a block of contigu-

ous ﬁres taken from the regular grid of ﬁre ignitions.

For each cluster of simultaneous ﬁres, the CA steps

are iterated until the current time p

reaches the ﬁnal

time. In the parallel implementation, each CA step es-

sentially consists of the two CUDA kernels mentioned

above plus the device-to-device memory copy opera-

tion to re-initialise the current values of the substates

with the next values.

At the end of each group of simulations, a further

CUDA kernel is launched on the whole automaton to

update an array f

in which each element represents

the number of times that a cell has been burned since

the beginning of the process. As soon as all the sched-

uled simulations have been carried out, each element

of the array f

, divided by the total number of simu-

lations, gives an estimate of the burn probability for

one of the cells.

5 RESULTS ON A REAL

LANDSCAPE

The preliminary application presented here concerns

an area of the Ligury region, in Italy, historically

characterized by a high frequency of serious wild-

ﬁres. The landscape, shown in Figure 6 was mod-

elled through a Digital Elevation Model composed of

461 × 445 square cells with side of 40 m. In the area,

the terrain is relatively complex with an altitude above

sea level ranging from 0 to 250 m. The heterogeneous

fuel bed depicted in Figure 6, was based on the use of

the 1:25000 land cover map from the CORINE EU-

project. The CORINE land-cover codes were mapped

on the standard fuel models used by the CA (i.e., the

substate µ). Plausible values of fuel moisture content

were obtained from literature data. Also, a domain-

averaged open-wind vector from the North direction,

having an intensity of 20 kmh

−1

, was used for produc-

ing time-constant gridded winds through WindNinja

(Forthofer et al., 2009), a computer program that sim-

ulates the effect of terrain on the wind ﬂow. A du-

SIMULTECH2012-2ndInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

266

Figure 6: The landscape under study: a 18km × 18km area in Ligury, Italy. Colors refer to the standard CORINE land-cover

data.

ration of 10 hours was adopted for all simulated ﬁres.

Over the area, a regular grid of 91 ×88 ignition points

was superimposed, leading to 8008 ﬁres to simulate.

Two CUDA graphic devices were used in the ex-

periments: a nVidia high-end Tesla C1060 and a

nVidia Geforce GT430 graphic card. In Table 1 some

of the relevant characteristics of the used GPGPU

devices are reported. The sequential programs, im-

plementing the same algorithms parallelised for the

GPGPU version, were run on a desktop computer

equipped with a 2.66 Ghz Intel Core 2 Quad CPU.

The two different implementations SCA and OCA de-

scribed in Section 4 were run on both the CPU and

GPU devices. In both cases, during the computation

process, 196 wildﬁres at a time were activated in or-

der to attain a satisfactory level of saturation of the

graphic device (see section 4).

The hazard map obtained after the n = 8008 sim-

ulations is shown in Figure 7. As shown in Table 2,

using the CPU the task took about 2.37 h for the SCA

version and about 1.44 h for the OCA implementa-

tion. As it can be seen in the same Table 2, the gain

provided by the parallelisation in terms of comput-

ing time is signiﬁcant. In particular, through the most

powerful GPGPU the BPM computation took only 5

minutes using the SCA implementation and about 3.5

Table 1: Characteristics of the adopted GPGPU hardware

for all carried out experiments.

GT430 Tesla C1060

Compute capability 2.1 1.3

CUDA cores 96 240

Global memory [MB] 1024 4096

Clock rate [MHz] 1400 1300

Bandwidth [GB/s] 28.8 102.4

GFLOPs 268.8 922.12

Table 2: Elapsed times (in seconds) for the computation of

the BPM shown in Figure 7.

SCA OCA

CPU 8518.2 5185.6

GT430 771.6 417.5

Tesla C1060 301.7 209.1

Table 3: Parallel speedup achieved with the used GPGPU

devices.

SCA OCA

GT430 11.0 12.4

Tesla C1060 28.2 24.8

minutes using the OCA. Interestingly, even by using

the consumer-level GPGPU GT430, the computation

took only a few minutes.

According to Table 3, where the results in terms

of parallel speedups are shown, the highest speedup

of 28.2 was achieved by the Tesla C1060 using the

SCA approach. Overall, the results in terms of time

savings are signiﬁcant, also considering the relatively

little effort required to develop the parallel versions of

the BPM computation algorithms. As before, it is also

worth noting that the GT430 graphic card, which pro-

vided here a parallel speedup of more than 10, costs

less than 60 Euros at the time of this publication.

As GPUs are specialized for single-precision cal-

culations, comparison tests were eventually carried

out with the aim of verifying the precision of results

between CPU-based outputs and GPUs’ ones. Here,

results were satisfactory, since the areal extensions of

simulations resulted the same, except for few approxi-

mation errors, limited to the 4

signiﬁcant digit place,

in a limited number of cells.

FastAssessmentofWildfireSpatialHazardwithGPGPU

267

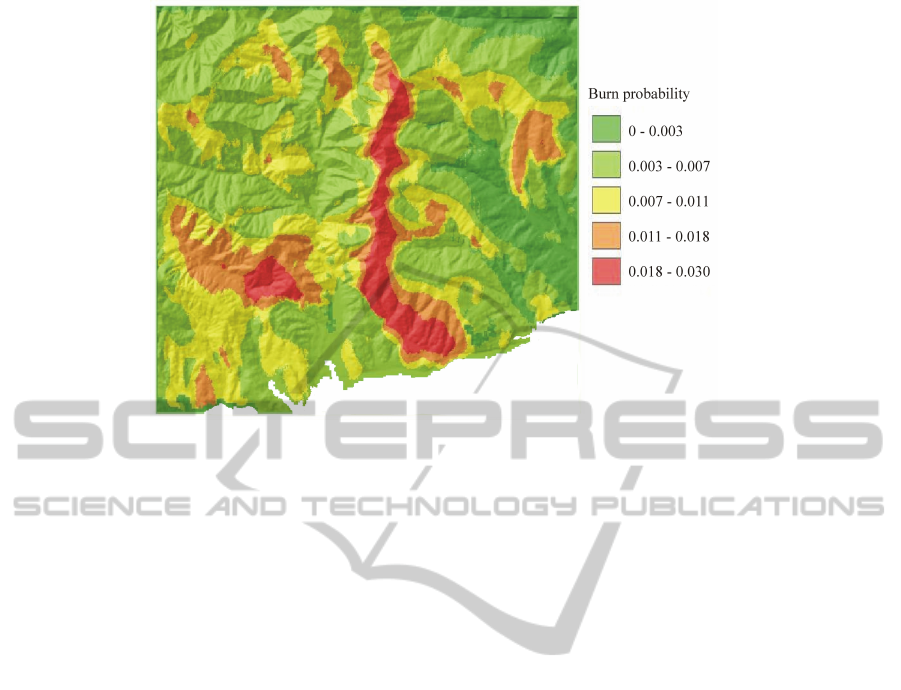
Figure 7: The BPM obtained for the landscape under study.

6 CONCLUSIONS AND FUTURE

WORK

The results in terms of parallel speedup of the

GPGPU-based BPM computation procedure pre-

sented above are indeed very encouraging. The main

advantage of such a parallelisation lies in enabling the

building of BPMs for large areas (e.g. at a regional

level), which otherwise may not be possible by adopt-

ing standard architectures.

Nevertheless, since not all the available GPGPU

optimization strategies have been implemented, am-

ple margins of speedup improvement are still pos-

sible. For example, since the only active cells are

the ones on the current ﬁre front, even the OCA ap-

proach described above can permit to launch a sig-

niﬁcant number of kernels on cells which are inac-

tive. A more advanced strategy could be used to map

mono-dimensional execution blocks only on the min-

imal number of cells lying on the ﬁre front. An em-

pirical investigation will determine whether the com-

plexity related to the building of such complex grid

mapping would be compensated by the fewer kernels

to launch at each step of the automaton.

Another possible direction of research consists of

making available the GPGPU approach in more gen-

eral libraries for supporting CA modelling and sim-

ulation, such as the one presented in (Blecic et al.,

2009).

ACKNOWLEDGEMENTS

This work was partially funded by the European Com-

mission - European Social Fund (ESF) and by the Re-

gione Calabria (Italy).

REFERENCES

Ager, A. and Finney, M. (2009). Application of wildﬁre

simulation models for risk analysis. In Geophysical

Research Abstracts, Vol. 11, EGU2009-5489, EGU

General Assembly.

Alexander, M. (1985). Estimating the length-to-breadth ra-

tio of elliptical forest ﬁre patterns. In Proc. 8th Conf.

Fire and Forest Meteorology, pages 287–304.

Anderson, H. (1983). Predicting wind-driven wildland ﬁre

size and shape. Technical Report INT-305, U.S De-

partment of Agriculture, Forest Service.

Andrews, P. (1986). BEHAVE: ﬁre behavior prediction and

fuel modeling system - burn subsystem, part 1. Tech-

nical Report INT-194, U.S Department of Agriculture,

Forest Service.

Blecic, I., Cecchini, A., and Trunﬁo, G. A. (2009). A

general-purpose geosimulation infrastructure for spa-

tial decision support. Transactions on Computational

Science, 6:200–218.

Carmel, Y., Paz, S., Jahashan, F., and Shoshany, M.

(2009). Assessing ﬁre risk using monte carlo simula-

tions of ﬁre spread. Forest Ecology and Management,

257(1):370 – 377.

Cui, W. and Perera, A. H. (2008). A study of simulation

errors caused by algorithms of forest ﬁre growth mod-

els. Technical Report 167, Ontario Forest Research

Institute.

SIMULTECH2012-2ndInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

268

Filippone, G., Spataro, W., Spingola, G., D’Ambrosio, D.,

Rongo, R., Perna, G., and Di Gregorio, S. (2011).

GPGPU programming and cellular automata: Imple-

mentation of the sciara lava ﬂow simulation code. In

23rd European Modeling and simulation Symposium

(EMSS), Rome, Italy.

Forthofer, J., Shannon, K., and Butler, B. (2009). Simu-

lating diurnally driven slope winds with windninja. In

Proceedings of 8th Symposium on Fire and Forest Me-

teorological Society - Kalispell, MT.

French, I., Anderson, D., and Catchpole, E. (1990). Graphi-

cal simulation of bushﬁre spread. Mathematical Com-

puter Modelling, 13:67–71.

Johnston, P., Kelso, J., and Milne, G. (2008). Efﬁcient sim-

ulation of wildﬁre spread on an irregular grid. Inter-

national Journal of Wildland Fire, 17:614–627.

Kourtz, P. H. and O’Regan, W. G. (1971). A model for a

small forest ﬁre to simulate burned and burning ar-

eas for use in a detection model. Forest Science,

17(7):163–169.

Krger, F., Maitre, O., Jimenez, S., Baumes, L., and Collet, P.

(2010). Speedups between x70 and x120 for a generic

local search (memetic) algorithm on a single gpgpu

chip. In Di Chio, C., Cagnoni, S., Cotta, C., Ebner, M.,

art, A., Esparcia-Alcazar, A., Goh, C.-K., Merelo,

J., Neri, F., Preu, M., Togelius, J., and Yannakakis, G.,

editors, EvoNum 2010, volume 6024 of LNCS, pages

501–511. Springer Berlin / Heidelberg.

Lopes, A. M. G., Cruz, M. G., and Viegas, D. X. (2002).

Firestation - an integrated software system for the

numerical simulation of ﬁre spread on complex to-

pography. Environmental Modelling and Software,

17(3):269–285.

McAlpine, R., Lawson, B., and Taylor, E. (1991). Fire

spread across a slope. In Proceedings of the 11th

Conference on Fire and Forest Meteorology (Society

of American Foresters: Bethesda, MD), pages 218–

225.

Miyamoto, H. and Sasaki, S. (1997). Simulating lava ﬂows

by an improved cellular automata method. Computers

& Geosciences, 23(3):283–292.

NVidia corp. (2010). CUDA C Programming Guide v. 3.2.

NVidia corp. (2012). CUDA C Best Practices Guide.

O’Regan, W. G., Kourtz, P., and Nozaki, S. (1976). Bias

in the contagion analog to ﬁre spread. Forest Science,

22.

Pallipuram, V., Bhuiyan, M., and Smith, M. (2011). A com-

parative study of GPU programming models and ar-

chitectures using neural networks. The Journal of Su-

percomputing, pages 1–46.

Peterson, S. H., Morais, M. E., Carlson, J. M., Denni-

son, P. E., Roberts, D. A., Moritz, M. A., and Weise,

D. R. (2009). Using HFIRE for spatial modeling of

ﬁre in shrublands. Technical Report PSW-RP-259,

U.S. Department of Agriculture, Forest Service, Pa-

ciﬁc Southwest Research Station, Albany, CA.

Preis, T. (2011). GPU-computing in econophysics and sta-

tistical physics. The European Physical Journal - Spe-

cial Topics, 194(1):87–119.

Roberts, M., Sousa, M. C., and Mitchell, J. R. (2010). A

work-efﬁcient gpu algorithm for level set segmenta-

tion. In ACM SIGGRAPH 2010 Posters, SIGGRAPH

’10, pages 53:1–53:1, New York, NY, USA. ACM.

Rongo, R., Lupiano, V., Avolio, M. V., D’Ambrosio, D.,

Spataro, W., and Trunﬁo, G. A. (2011). Cellular au-

tomata simulation of lava ﬂows - applications to civil

defense and land use planning with a cellular automata

based methodology. In Kacprzyk, J., Pina, N., and

Filipe, J., editors, SIMULTECH 2011, pages 37–44.

SciTePress.

Rongo, R., Spataro, W., D’Ambrosio, D., Avolio, M. V.,

Trunﬁo, G. A., and Gregorio, S. D. (2008). Lava ﬂow

hazard evaluation through cellular automata and ge-

netic algorithms: an application to mt etna volcano.

Fundam. Inform., 87(2):247–267.

Rothermel, R. C. (1972). A mathematical model for pre-

dicting ﬁre spread in wildland fuels. Technical Re-

port INT-115, U.S. Department of Agriculture, Forest

Service, Intermountain Forest and Range Experiment

Station, Ogden, UT.

Rothermel, R. C. (1983). How to predict the spread and in-

tensity of forest and range ﬁres. Technical Report INT-

143, U.S. Department of Agriculture, Forest Service,

Intermountain Forest and Range Experiment Station,

Ogden, UT.

Sullivan, A. (2009). Wildland surface ﬁre spread mod-

elling, 1990-2007. 3: Simulation and mathematical

analogue models. International Journal of Wildland

Fire, 18:387–403.

Szerwinski, R. and G

uneysu, T. (2008). Exploiting the

power of GPUs for asymmetric cryptography. In Pro-

ceedings of the 10th International Workshop on Cryp-

tographic Hardware and Embedded Systems (CHES

2008), pages 79–99, Washington, DC, USA.

Trunﬁo, G. A. (2004). Predicting wildﬁre spreading through

a hexagonal cellular automata model. In Sloot,

P. M. A., Chopard, B., and Hoekstra, A. G., edi-

tors, ACRI, volume 3305 of LNCS, pages 385–394.

Springer.

Trunﬁo, G. A., D’Ambrosio, D., Rongo, R., Spataro, W.,

and Gregorio, S. D. (2011). A new algorithm for simu-

lating wildﬁre spread through cellular automata. ACM

Trans. Model. Comput. Simul., 22(1):6.

Yassemi, S., Dragicevic, S., and Schmidt, M. (2008). De-

sign and implementation of an integrated GIS-based

cellular automata model to characterize forest ﬁre be-

haviour. Ecological Modelling, 210(1-2):71–84.

FastAssessmentofWildfireSpatialHazardwithGPGPU

269