A Dimension Integration Method for a Heterogeneous Data Warehouse
Environment
Marius-Octavian Olaru and Maurizio Vincini
Department of Information Engineering, University of Modena, Via Vignolese 905, 41125 Modena, Italy
Keywords:
Multidimensional Schema Matching, Dimension Merging.
Abstract:
Data Warehousing is the main Business Intelligence instruments that allows the extraction of relevant, aggre-
gated information from the operational data, in order to support the decision making process inside complex
organizations. Following recent trends in Data Warehousing, companies realized that there is a great potential
in combining their information repositories in order to offer all participants a broader view of the economical
market. Unfortunately, even though Data Warehouse integration has been defined from a theoretical point of
view, until now no complete, widely used methodology has been proposed to support Data Warehouse in-
tegration. This paper proposes a method that is able to achieve both schema and instance level integration
of heterogeneous Data Warehouse dimensions attributes by exploiting the topology of dimensions and the
dimension-chase procedure.
1 INTRODUCTION
During the last two decades, Data Warehousing (DW)
has been the main Business Intelligence (BI) instru-
ment for the analysis of large banks of operational
data. It allows managers to take strategic decisions
based on aggregatedinformationsynthesized from the
operational data.
In recent years, however, managers realized that
new opportunities can be obtained from the Data
Warehouse by combining information coming from
more than one company, allowing them to have a
broader view of the economical market. For exam-
ple, it is common nowadays for two or more compa-
nies to merge, or to collaborate in a federation-like
environment. In both cases, the Data Warehouses of
the independent companies have to be combined in
order to provide an unified view over the entire avail-
able information. The widest used approach, is to ex-
tract data from the repositories of all the participants
through complex Extract-Transform-Load(ETL) pro-
cesses, and then to rebuild the DW from the unified
data repository. Apart from being a complicated ap-
proach due to the heterogeneity of the data reposi-
tories, this solution involves an enormous amount of
work and it usually has high costs and long develop-
ment times.
This approach may be considered a low-end so-
lution, as the actual integration is being made at the
early stages of the Data Warehouse building proce-
dure. A more elegant solution would be to make a
high-end integration of the DWs. Although this ap-
proach may seem less time and resource consuming,
it presents nevertheless several difficulties, mainly de-
riving from the heterogeneity of the information and
from the fact that the information to integrate is mul-
tidimensional.
In this paper we present a method for DW inte-
gration, that is able to (1) generate a set of consis-
tent mappings between heterogeneous DW dimension
levels, (2) import remote compatible dimensional at-
tributes in a local schema and (3) populate the newly
imported attributes with consistent information from
the remote dimensional attribute.
The rest of this paper is organized as follows:
Section 2 provides an overview on related work;
Section 3 describes a technique to generate map-
ping predicates between heterogeneous DW dimen-
sion levels, while Section 4 describes the schema im-
portation procedure. Finally, Section 5 draws the con-
clusions and provides an overview on possible future
work.
2 RELATED WORK
Until now there have been few formalization attempts
to solve the DW integration problem, and to the
278
Olaru M. and Vincini M..
A Dimension Integration Method for a Heterogeneous Data Warehouse Environment.
DOI: 10.5220/0004071702780283
In Proceedings of the International Conference on Data Communication Networking, e-Business and Optical Communication Systems (ICE-B-2012),
pages 278-283
ISBN: 978-989-8565-23-5
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

knowledge of the authors, no complete methodology
for the high-end DW integration has been proposed.
Some papers formalize, in some extent, the con-
cept of similar multidimensional schemas. For ex-
ample, (Golfarelli et al., 1998) defines the concept
of compatible schemas and provides a method for
computing the overlap of two DFM schemas, while
(Cabibbo and Torlone, 2004) defines a Dimension Al-
gebra (DA) that is then used to formalize the inter-
section of compatible dimensions. Although the DA
can be used to formalize the solution for dimension
integration, the paper doesn’t provide a methodology
for computing the DA expressions that can be used
for integration purposes.
The work presented in (Banek et al., 2008) pro-
poses a linguistic and structure based similarity func-
tion for multidimensional structures. The proposed
method is inspired from classical data integration ap-
proaches (like (Beneventano et al., 2003; Madhavan
et al., 2001; Melnik et al., 2002)), where designers
make use of affinity functions to express similarities
between attributes and classes. Although a similar
approach may be used for the integration of hetero-
geneous DWs, we believe that the particular proper-
ties of the multidimensional structures that character-
ize the DWs can yield better results.
Am innovative architecture for the integration of
heterogeneous DWs is proposed in (Golfarelli et al.,
2010; Golfarelli et al., 2011), where the authors
present the concept of Business Intelligence Network
which is a peer-to-peer like network of DWs. The au-
thors make use of mapping predicates to express sim-
ilarity among concepts; unfortunately no automatic
procedure for identifying the mapping predicates is
provided.
3 DIMENSION MAPPING
STRATEGY
The first step of the method is to find similar dimen-
sion levels inside two dimension hierarchies. For this
purpose, one may use classical data-integration ap-
proaches, like semantics or similarity measurement
functions (see (Calvanese et al., 2001) for an exam-
ple). However, even if in such a way it is possible
to find semantically similar elements, we believe that
such approach will not be able to provide the required
accuracy in a multidimensional environment. The
main reason is that two similar, but different dimen-
sions, may contain related information (like a time hi-
erarchy), but structured differently. This may lead to
inconsistent analysis capabilities. Consider, for ex-
ample, the dimensions in Figure 1. Suppose the first
schema (call it S
1
) contains the REVENUE fact table
of a Data Warehouse (call it DW
1
), and that the second
schema (S
2
) contains the SALE fact schema from an-
other Data Warehouse (call it DW
2
). Suppose that the
goal is to integrate the information coming from the
two DWs, and that managers have to be able to query
them contemporaneously and to obtain an unified an-
swer. In some cases, this is straightforward, in other
cases it may raise some issues. For example, the total
revenue divided by city and month may be obtained
by combining the revenue from every individual DW,
divided by city and month. Note that this query is
possible because the required information is available
in both DWs, at the required granularity. The only
extra required information is that the dimension level
S
1
.city is equivalent to the dimensional level S
2
.city,
and that the same may be said for the dimensional
level month.
3.1 Equivalent Nodes Detection
In order to automatically detect pairs of equivalent di-
mension levels, the method we propose makes use of
the topology of dimensions. In fact, dimensions usu-
ally maintain a tree-like structure imposed by the par-
tial order relationship on the dimensional attributes
set. This property is maintained when dimensions
represent a concept of the real world with a common
structure. Consider, for example, that the time dimen-
sion of the instance of S
1
contains all the days from
January 1
st
2007 to December 31
st
2010 (4 complete
years), and that the time dimension of the schema S
2
contains all the days from January 1
st
2009 to De-
cember 31
st
2011 (3 complete years). Although the
sets of the values of the attributes are only partially
overlapped, this information may not be sufficient to
discover semantic equivalences.
The method proposed in this paper relies instead
on another property of dimension hierarchies, that we
call cardinality-ratio. The cardinality-ratio is sim-
ply the ratio among the number of different elements
between two dimension hierarchy levels. For exam-
ple, in the time dimension in schema S
1
, every el-
ement of the month level is an aggregation of ap-
proximately 30 different elements of the day level.
Although it covers a different time period, the same
property can be observed in the second time dimen-
sion. This information is maintained not only be-
tween directly connected dimension hierarchies. For
example, in the schema S
2
a year is an aggregation
of 12 different months. In schema S
1
, a year is com-
posed of 2 semesters, every semester is composed of
2 trimesters, where each trimester is composed of 3
different months. This means that a year is an ag-
ADimensionIntegrationMethodforaHeterogeneousDataWarehouseEnvironment
279

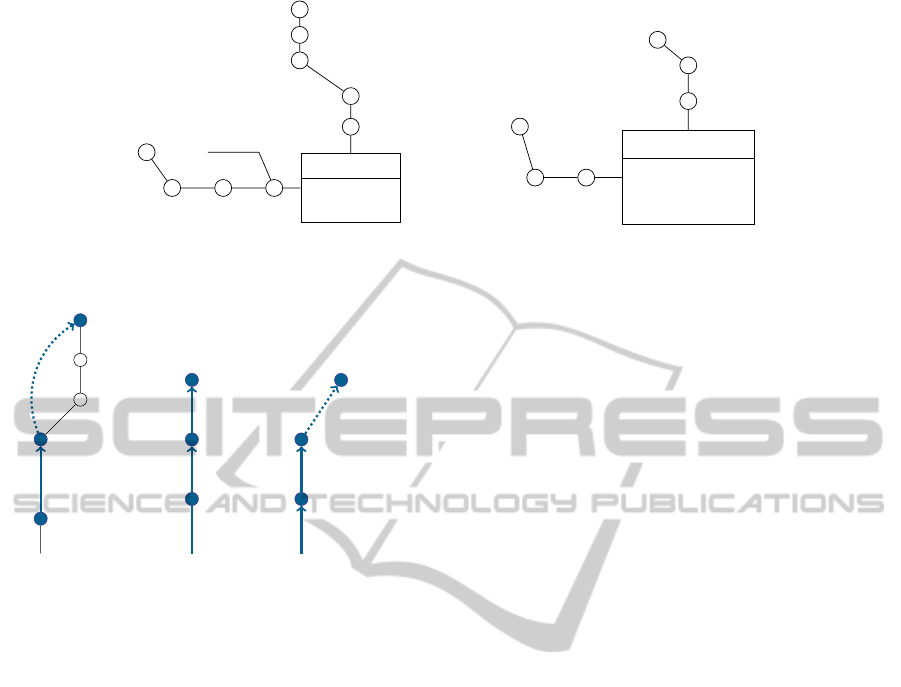
REVENUE
amount
day
month
trimester
semester
year
clientcityregion
country
address
(a) S
1
schema.
SALE(S
2
)
qty sold
revenue
no. of customers
day
month
year
clientcity
country
(b) S
2
schema.
Figure 1: Example.
day
month
trimester
semester
year
30
12
(a) First graph.
day
month
year
30
12
(b) Second
graph.
day
month
year
30
12
(c) Common
subgraph.
Figure 2: Dimension graphs.
gregation of 2 × 2× 3 different months, which is the
same information that is directly available in the other
hierarchy.
This property may be used not only on time di-
mensions, but on all dimensions that represent a con-
cept of the real world with a fixed structure. For ex-
ample, the geographical distribution inside one coun-
try is likely to be similar among all DWs that contain
that particular geographical distribution. An address
refers to a city, a city refers to a region, a region refers
to a country.
In order to identify similar dimensional attributes,
we first consider the dimension hierarchies as directed
labeled graphs, where the dimension hierarchy lev-
els are the nodes of the graphs and the label of each
edge is the cardinality-ratio among different elements.
Figure 2(a) is a directed labeled graph that represents
the time dimension of the first schema (S
1
), while
Figure 2(b) represents the dimension of the second
schema (S
2
). Starting from these two graphs, it is pos-
sible to compute a common subgraph (Figure 2(c))
that can be used to identify pairs of equivalent nodes
in the initial graphs.
The common sub-graph may be obtained from
the first graph by eliminating the nodes trimester
and semester, and by adding the directed edge
(month, year) (represented as dotted in Figure 2(a)).
The common sub-graph is then used to map elements
of the initial graphs. For example, the node day of
the common subgraph is obtained from the node day
of the first graph, or from the node with the same
name of the second graph. This implies that nodes
S
1
.day is equivalent to node S
2
.day. Following the
same approach, S
1
.month is equivalent to S
2
.month
and S
1
.year is equivalent to S
2
.year.
3.2 Mapping Set Generation
In order to express the complex relationships among
various dimension levels, we make use of a subset of
the mapping predicates proposed in (Golfarelli et al.,
2010), in particular:
• Equi-level Predicate: used to state that two at-
tributes in two different md-schemas have the
same granularity and meaning;
• Roll-up Predicate: used to indicate that an at-
tribute (or set of attributes) of the first md-schema
aggregates an attribute (or set of attributes) of the
second md-schema;
• Drill-down Predicate: used to indicate that an at-
tribute (or set of attributes) of the first md-schema
disaggregates an attribute (or set of attributes) of
the second md-schema;
• Related Predicate: indicates that between two at-
tributes there is a many−to− many relation;
To generate the complete mapping set, we make
use of the following inference rules:
Let P
x
and P
y
be two nodes of the first graph such
that there is a path from P
x
to P
y
, and P
h
and P
k
two nodes of the second graph such that there is a
path from P
h
and P
k
1. Rule 1: If P
x
and P
h
are equivalent, add the map-
ping:
* P
x
(equi− level) P
h
ICE-B2012-InternationalConferenceone-Business
280

2. Rule 2: if P
x
(equi−level) P
h
, add the mappings:
* P
y
(roll − up) P
h
* P
h
(drill − down) P
y
(See Figure 3(a))
3. Rule 3: if P
y
(equi−level) P
h
, add the mappings:
* P
x
(drill − down) P
h
* P
h
(roll − down) P
x
(See Figure 3(b))
4. Rule 4: if P
y
(equi−level) P
h
, add the mappings:
* P
x
(drill − down) P
k
* P
k
(roll − up) P
x
(See Figure 3(c))
5. Rule 5: for every nodes P
x
and P
h
of the two
graphs for which there has not been found any
mapping rule, add the mapping:
* P
x
(related) P
h
P
y
P
x
P
h
(equi-level)
(drill −down)
(roll −up)
(a) Rule 2.
P
y
P
h
P
x
(equi-level)
(drill −down)
(roll −up)
(b) Rule 3.
P
k
P
y
P
h
P
x
(equi-level)
(drill −down)
(roll −up)
(c) Rule 4.
Figure 3: Graphical representation of rules 2, 3 and 4.
4 DIMENSION MERGING
The mappings discovered in Section 3 can be used to
formulate queries on a set of compatible Data Ware-
houses, using query rewriting techniques. A major
drawback of this approach is that the query rewrit-
ing accuracy depends on the compatibility of the
schemas. For example, considering the schemas in
Figure 1, a possible query would be to obtain the to-
tal revenue divided by city and month. This query is
compatible, as the required information is available
in both Data Warehouses, at the required level of ag-
gregation. However, other queries are incompatible.
For example, on the schema S
1
it is possible to ex-
ecute a query to obtain the total revenue, divided by
region and month. In this case however, the query
would return only information coming from DW
1
, as
the expressed query cannot be formulated on DW
2
.
One way of bypassing this problem is to uni-
form the analysis capabilities of the peers, by making
the dimensions as similar as possible. This may be
achieved, for example, by importing, where possible,
compatible parts of remote DW dimensions.
4.1 Partial Schema Importation
The presence of at least one <equi-level> mapping
suggests that the two dimensions have common infor-
mation, so their schemas are overlapped, as defined
in (Golfarelli et al., 1998). The key idea is to use that
common schema information as a starting point for
importing other dimensional attributes. The attributes
are first inserted as optional attributes, and then, if suf-
ficient information is available in the two DWs, the
attributes are modified to mandatory attributes.
For example, consider that by exploiting the
method proposed in Section 3, we obtain the follow-
ing mappings:
• ω
1
: S
1
.city <equi-level>S
2
.city (Rule 1).
• ω
2
: S
1
.country <equi-level>S
2
.country (Rule 1).
• ω
3
: S
1
.region <roll-up>S
2
.city (Rule 2).
• ω
4
: S
1
.region <drill-down>S
2
.country (Rule 3).
If it were possible to import the region attribute
inside the schema S
2
, then queries involving the geo-
graphical hierarchy may be expressed on both DWs,
with the same query answering capabilities. The in-
tegration, however, must be done at both schema and
instance level.
To formalize this step, we decided to use Dimen-
sional Fact Model (Golfarelli et al., 1998), mainly
because this particular model defines the concept of
optional dimensional attribute. The DFM describes
a fact schema as a sextuple f = (M, A, N, R, O, S),
where:
• M is a set of measures defined by a numeric or
Boolean value.
• A is a set of dimensional attributes.
• N is a set of non-dimensional attributes.
• R is a set of ordered couples that define the
quasi−tree representing the dimension hierarchy.
• O ⊆ R is a set of optional relationships.
• S is a set of aggregation statements.
ADimensionIntegrationMethodforaHeterogeneousDataWarehouseEnvironment
281

(d
1
)
city
region
country
(d
2
)
city
region
country
equi− level
Figure 4: Graphical example of the importation rule.
The first step of the schema importation procedure is
based on the following rule:
Rule 1. Given two fact schemas
f
1
= (M
′
, A
′
, N
′
, R
′
, O
′
, S
′
) and f
2
=
(M
′′
, A
′′
, N
′′
, R
′′
, O
′′
, S
′′
), and the set M of map-
pings between the two schemas, let a
′
i
, a
′′
i
∈ A
′
such that (a
′
i
, a
′′
i
) ∈ R
′
, and a
′
j
∈ A
′′
. If
{(a
′
i
< equi− level > a
′
j
), (a
′′
i
< roll − up > a
′
j
)} ⊆
M , then:
A
′′
:= A
′′
∪ {a
′′
i
} (1)
O
′′
:= O
′′
∪ {(a
′
j
, a
′′
i
)}
If ∃ a
′′
j
∈ A
′′
such that {(a
′
j
, a
′′
j
)} ⊆ R
′′
, and
{(a
′′
i
< drill − down > a
′′
j
)} ⊆ M , then:
R
′′
:= R
′′
∪ {(a
′′
i
, a
′′
j
)} (2)
Figure 4 contains a graphical example of the im-
portation Rule. Dimensions d
1
and d
2
are the corre-
sponding dimensions of DW
1
and DW
2
as defined in
Figure 1. As region, city ∈ A
′
and (city,region) ∈ R
′
and city ∈ A
′′
, and (S
1
.region < roll − up > S
2
.city),
then, according to (1), the attribute region is in-
serted among the attributes of S
2
and the ordered tu-
ple (city, region) is inserted in O
′′
. Then, for every
dimensional attribute in A
′′
that is a roll − up of the
newly inserted attribute, an ordered couple is added
to R
′′
, in order to express the given semantic relation.
As S
2
.country < roll − up > S
1
.region, the ordered
couple (region, country) is inserted in R
′′
.
4.2 Data Importation
In order to import information from remote dimen-
sions, the dimension-chase (Torlone, 2008) (or d-
chase) algorithm is used. The d-chase procedure is a
derivation of the chase algorithm presented in (Abite-
boul et al., 1995) for reasoning on dependencies in re-
lational databases. The procedure consists in creating
an initial tableau from the dimensions and applying
a chase step recursively until the completion of the
tableau.
With a little abuse of notation, the information
contained in the two dimensions will be represented
as a table. Table 1 represents the initial tableau, built
by adding all the attributes of the two dimensions (the
couples of attributes in the two dimensions that are
connected by an < equi− level > relation are inserted
only once, as they represent the same concept). The
tuples in the table are the tuples of the dimensions.
For every column representing an attribute not con-
tained in the dimension, the value is replaced by a
variable (see last three rows). Suppose that the first
three rows represent the information contained in the
first dimensions (d
1
), while the last three rows repre-
sent the information from the second dimension (d
2
).
The chase-step consists in recursively applying the
following rule:
Rule 2. ∀a
1
, a
2
∈ A
′
such that (a
1
, a
2
) ∈ R
′
, or
a
1
, a
2
∈ A
′′
such that (a
1
, a
2
) ∈ R
′′
, if ∃ t
1
,t
2
∈ T such
that t
1
[a
1
] = t
2
[a
1
] and t
1
[a
2
] 6= t
2
[a
2
], then if t
1
[a
2
] is
a variable, assign it the value t
1
[a
2
] := t
2
[a
2
] (vice-
versa if t
2
[a
2
] is a variable).
The chase ends after no possible assignment
can be made using the information available in the
tableau. In the given example, the procedure success-
fully assigns v
1
the value ”ER” and to v
2
the value
”TO”. However, no value is assigned to variable v
3
,
because no sufficient information is contained in the
first dimension. The final tableau can be used to im-
port the required information in the second dimen-
sion. First of all, the tableau needs to be projected on
the final schema of the dimension in which to import
the information (d
2
in the example), in order to import
the values of the dimension levels of interest. There
are two aspects of the information importation step.
First of all, the newly inserted dimensional attribute
(region) is populated with compatible values found in
the other dimension. Secondly, the importation step
increases the information previously available in the
initial dimension, due to the possibility of importing
the tuples from the tableau originated from the remote
dimension (d
1
in our case).
As stated earlier, if sufficient information is con-
tained in the two dimensions, then the attribute orig-
inally inserted (region) can be promoted to a normal
attribute. This is possible only if the values of the
newly inserted attribute have all been populated. Us-
ing the tableau, this is true only if all variables in the
column have been assigned a value from the other di-
mension. This is not the case in our example, as vari-
able v
3
has been assigned no value after the execution
of the d-chase algorithm.
ICE-B2012-InternationalConferenceone-Business
282

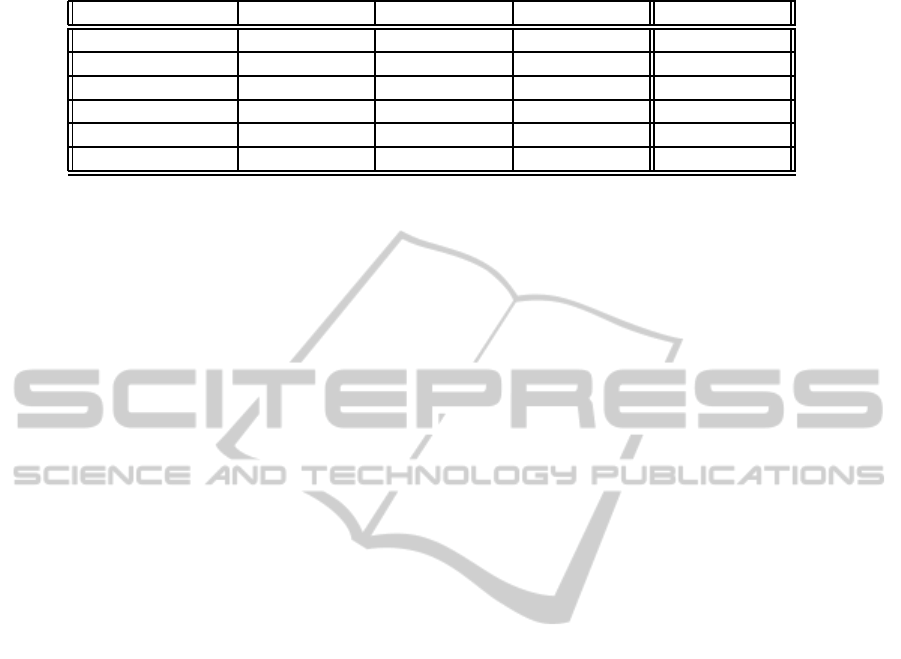
Table 1: Tableau.
client city region country dimension
M.ROSSI MODENA ER ITALY d1
P.BIANCHI FLORENCE TO ITALY d1
A.RENZO BOLOGNA ER ITALY d1
A.MANCINO MODENA v1 ITALY d2
S.RUSSO FLORENCE v2 ITALY d2
T.CONTI ROME v3 ITALY d2
5 CONCLUSIONS
The work presented in this paper describes a method
for the integration of heterogeneous Data Warehouse
dimensions. The main conclusion that can be drawn
from the paper is that the particular multidimensional
structure of DW information may be successfully ex-
ploited together with other classical data integration
approaches/techniques(like the d-chase procedure) to
achieve DW integration.
The method proposed in the paper is divided into
two steps. First, topological properties are used to
generate a mapping set between various dimension
levels, then, compatible schema parts, and the infor-
mation that is populated by, are integrated. The steps
can be independently modified in order to increase the
accuracy. In fact, one area of possible future work
is to expand the mapping generating step by using
a mixture of approaches, for example by adding the
use of semantics. It has been proven in classical data-
integration (for example (Bergamaschi et al., 2007))
that a combined approach usually increases the accu-
racy of the mapping generation step.
Another challenging problem in DW integration
that we believewill be the fruit of intensiveresearch is
the final integration of multidimensional information.
Although it relies on mapping predicates, this partic-
ular step will raise some issues, like the discovery of
common information which needs to be identified in
order to maintain the final result unalterated.
REFERENCES
Abiteboul, S., Hull, R., and Vianu, V. (1995). Foundations
of Databases. Addison-Wesley.
Banek, M., Vrdoljak, B., Tjoa, A. M., and Skocir, Z. (2008).
Automated Integration of Heterogeneous Data Ware-
house Schemas. IJDWM, 4(4):1–21.
Beneventano, D., Bergamaschi, S., Gelati, G., Guerra, F.,
and Vincini, M. (2003). MIKS : An Agent Framework
Supporting Information Access and Integration. In
Klusch, M., Bergamaschi, S., Edwards, P., and Petta,
P., editors, AgentLink, volume 2586 of Lecture Notes
in Computer Science, pages 22–49. Springer.
Bergamaschi, S., Bouquet, P., Giacomuzzi, D., Guerra,
F., Po, L., and Vincini, M. (2007). An Incremental
Method for the Lexical Annotation of Domain Ontolo-
gies. Int. J. Semantic Web Inf. Syst., 3(3):57–80.
Cabibbo, L. and Torlone, R. (2004). On the Integration
of Autonomous Data Marts. In SSDBM, pages 223–.
IEEE Computer Society.
Calvanese, D., Castano, S., Guerra, F., Lembo, D., Mel-
chiori, M., Terracina, G., Ursino, D., and Vincini, M.
(2001). Towards a Comprehensive Methodological
Framework for Integration. In KRDB.
Golfarelli, M., Maio, D., and Rizzi, S. (1998). The Di-
mensional Fact Model: A Conceptual Model for Data
Warehouses. Int. J. Cooperative Inf. Syst., 7(2-3):215–
247.
Golfarelli, M., Mandreoli, F., Penzo, W., Rizzi, S., and Tur-
ricchia, E. (2010). Towards OLAP query reformula-
tion in Peer-to-Peer Data Warehousing. In Song, I.-
Y. and Ordonez, C., editors, DOLAP, pages 37–44.
ACM.
Golfarelli, M., Mandreoli, F., Penzo, W., Rizzi, S., and Tur-
ricchia, E. (2011). OLAP Query Reformulation in
Peer-to-Peer Data Warehousing. Information Systems.
Madhavan, J., Bernstein, P. A., and Rahm, E. (2001).
Generic Schema Matching with Cupid. In Apers, P.
M. G., Atzeni, P., Ceri, S., Paraboschi, S., Ramamoha-
narao, K., and Snodgrass, R. T., editors, VLDB, pages
49–58. Morgan Kaufmann.
Melnik, S., Garcia-Molina, H., and Rahm, E. (2002). Sim-
ilarity Flooding: A Versatile Graph Matching Algo-
rithm and Its Application to Schema Matching. In
ICDE, pages 117–128.
Torlone, R. (2008). Two approaches to the integration of
heterogeneous data warehouses. Distributed and Par-
allel Databases, 23(1):69–97.
ADimensionIntegrationMethodforaHeterogeneousDataWarehouseEnvironment
283