Some Remarks on Keystroke Dynamics

∗

Global Surveillance, Retrieving Information and Simple Countermeasures

Marek Klonowski, Piotr Syga and Wojciech Wodo

Faculty of Fundamental Problems of Technology, Wrocław University of Technology, Wrocław, Poland

Keywords:

User Identiﬁcation, Keystroke Dynamics, Digraphs, Distribution, Impersonation.

Abstract:

In this paper we discuss some security issues related to keystroke dynamics. Up to now these methods have

been used mainly for supporting authentication protocols. We point out that they can be also used against

privacy and potentially lead to some other malicious behavior like for example impersonation. We also present

some simple fairly realistic and usable countermeasures. We discuss fundamental issues about efﬁcient and

accurate representation of user’s proﬁle in keystroke dynamic methods. More precisely, we discuss statistics

of so–called timings used for building user’s proﬁle. We give some observations about distributions of timings

that substantially differ from assumptions used in numerous papers. Some of our theories are supported by

experimental results.

1 INTRODUCTION

Keystroke dynamics is one of the methods used

mainly for behavioral biometric authentication. Being

behavioral, thus more variable and less dependable,

biometric keystroke dynamics it is commonly used as

a secondary security mechanism typically with pass-

word authentication. This method requires no addi-

tional infrastructure and authentication is possible re-

motely. In our paper we discuss this behaviometrics

methods from a different perspective – we point out

some possible threats as well as some related issues

including representation of individuals’ proﬁles.

Our Contribution and Organization of the Paper.

In the rest of this section we recall some related re-

sults. Section 2 is devoted to description of possible

risks brought by keystroke methods. In Section 3 we

describe a number of issues related to representation

of user’s proﬁles - in particular we analyze statisti-

cal properties of so–called timings of n-graphs used

commonly as characteristic of individuals. We sup-

port some our conjectures with experimental results.

In Section 4 we outline several simple protocols for

protecting privacy and preventing impersonation-type

attacks. We conclude in Section 5.

∗

This research was partially supported by NCN/M-

NiSW scientiﬁc project 2010-2013 - grant number N N206

369839.

Related Work. There is a long list of papers as

well as implementations based on keystroke dynam-

ics. To the best of our knowledge in (Gaines et al.,

1980) authors presented their study about typing pat-

terns for the ﬁrst time. However, these observations

were not used in the context of behaviometrics un-

til the seminal paper (Joyce and Gupta, 1990), when

authors presented their algorithm to measure laten-

cies of pressing keys during typing and comparing

it with previously stored information. In (Cho and

Hwang, 2006) authors suggest using artiﬁcial rhythm

of typing and long pauses between some characters

to enhance security and in (Revett et al., 2007) au-

thors use neural networks to improve classiﬁcation

accuracy. In (Bergadano et al., 2002), followed by

(Zhang et al., 2006) a method of continuous iden-

tiﬁcation is proposed, where user’s activity is con-

stantly monitored and thus their typing latencies have

to be predicted. In (Stefan et al., 2012) authors make

ﬁrst attempt to implement software protecting from a

bot attacker. Many further references can be found

in (Chudá and Durﬁna, 2009; Revett, 2009). Prac-

tical use of keystroke data has been implemented in

BioPassword (BioPassword Inc., 2007) an authentica-

tion system that employs most of current knowledge.

296

Klonowski M., Syga P. and Wodo W..

Some Remarks on Keystroke Dynamics - Global Surveillance, Retrieving Information and Simple Countermeasures.

DOI: 10.5220/0004072602960301

In Proceedings of the International Conference on Security and Cryptography (SECRYPT-2012), pages 296-301

ISBN: 978-989-8565-24-2

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 GLOBAL RISK

In this section we point out some risks related to

methods of keystroke dynamics. Two main risks we

have in mind are

• Privacy threat - the individual can be recognized

against their will.

• Impersonation - someone can collect the biomet-

ric data and pretend to be a particular individual.

To the best of our knowledge those problems were

not addressed in literature except the paper (Stefan

et al., 2012), wherein authors study the threat of im-

personating user by a bot. Note that the privacy threat

is not limited to biometric authentication systems. In-

deed, collected data in one system can be used to rec-

ognize the user in other systems. Generally, such

attacks seem to be applicable to all biometric sys-

tems, however there are some peculiarities that in-

crease the risk that one can be recognized by char-

acteristic keystroke dynamics. Among most notable

risks are the following:

• data about keystroking of individuals can be col-

lected over long period of time leaving user un-

aware of such process;

• keyboards are still a very important and most

common computer interface device; most popu-

lation in many countries use systems with a key-

board to perform many operations including com-

munication, entertainment or various e-service;

• the users may unwittingly be susceptible to data

collection by various kinds of keyloggers while

performing their regular tasks;

• simple and compact data representation, results

in ease of collecting and storing the information

about keystroke patterns (i.e. proﬁles of users) for

huge number of individuals for a long time;

• collecting as well as storing information does not

require any signiﬁcant resources.

• to some extent, historical data can be used for a

long time. More precisely, to launch an attack the

adversary may use data much older than the secu-

rity mechanism that they try to by-pass.

Another fact that has to be underlined is that iden-

tiﬁcation using keystroke dynamics can be at least in

some cases carried out in a remote manner. When

using SSH1 protocol an eavesdropper can easily de-

rive inter-key times as every key-press generates data

package (see e.g. (Song et al., 2001)). Such attack

cannot be carried out easily using much more com-

mon nowadays SSH2. Nevertheless one cannot ex-

clude that similar attacks exist and can be exploited

while using other protocols.

Aforementioned facts make building user proﬁle

quite realistic. Moreover users are potentially ex-

posed to proﬁling attacks on different systems. Then

his proﬁle can be transfered and even if these destina-

tion systems employ some privacy protection means

his identity could be recovered. Let us stress that

we do not claim that such attacks can be realistic in

all cases. We do claim however that there are some

potential risks that should be investigated more care-

fully.

3 REPRESENTATION OF USER'S

PROFILE

In this section we discuss issues related to representa-

tion of a user’s proﬁle in widely-understood keystroke

dynamic methods. User’s typing behavior is reﬂected

in several values. The most general values are so-

called timings, or delays that occur when pressing var-

ious keys. In the literature of the subject one can en-

counter dwell time – the time between events of key

down and key up, ﬂight time – the time between press-

ing two consecutive keys. Two consecutive keys are

called digraph. By trigraphs we mean three consec-

utive keys and consequently we use term n-graphs to

describe n keys in a row.

One can easily see that timings for each digraph

for the same individual can differ - it is a random vari-

able. Collection of such random variables is a natural

representation of an individual. Below we give some

observations and experimental results about their dis-

tribution.

3.1 On Normality of Digraphs

In several papers there has been explicitly stated that

the ﬂight time for each single digraph could be as-

sumed Gaussian (i.e., (Monrose and Rubin, 1997;

Sheng et al., 2005; Zhang and Wang, 2009)). Such

approach seems to be essentially unjustiﬁed. In fact,

to the best of our knowledge, there is no reason why

ﬂight times could have normal distribution. In partic-

ular it is hard to use Central Limit Theorem in this

case. It should be stressed that in the paper (Sim and

Janakiraman, 2007) one can ﬁnd a suggestion that the

distribution of ﬂight times for digraphs is (in general)

not Gaussian. In this section we present some results

of statistical tests that say that digraph timings’ distri-

bution is not normally distributed.

Experimental Results. Let us start with method-

ological remarks. We have collected over 60 000 in-

dividual samples of digraphs with ﬂight time in range

SomeRemarksonKeystrokeDynamics-GlobalSurveillance,RetrievingInformationandSimpleCountermeasures

297

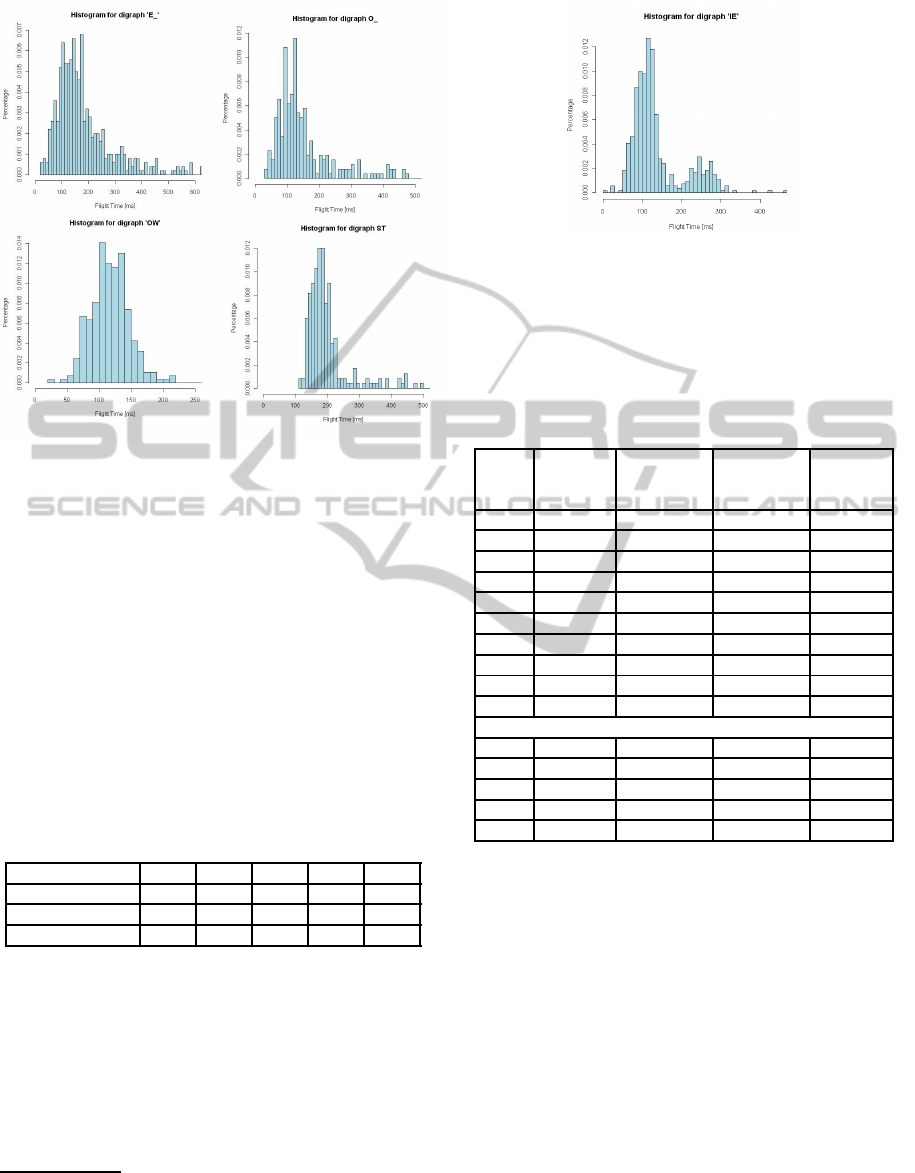
Figure 1: Distribution of ﬂight time timing for digraphs

"OW", "E_", "ST", "O_".

from 21 up to 800 ms. We rejected samples which

include ﬂight time greater than 800 ms treating them

as breaks in typing. Entire dataset was collected in a

controlled environment from trained typists, typing in

Polish as a native language

. The results are obtained

from form so-called free text – i.e., the data was col-

lected using special key-logger during regular work

of the typist. We believe that such approach reﬂects

real settings of keystroke dynamics.

Our ﬁrst goal was to examine whether the distri-

bution of the digraphs is normal. For tests we chose

digraphs with largest amounts of collected data to ob-

tain reliable results.

Table 1: Occurrence of ten the most common digraphs.

Digraph IE E_ A_ NI _P

Occurrence[%] 2.12 1.96 1.71 1.67 1.30

Digraph OW ” ZE _O PO

Occurrence[%] 1.11 1.07 1.06 1.01 1.00

Below we present histograms for some of investi-

gated digraphs.

Even perfunctory analysis of histograms suggests

that the distribution of timings of digraphs is not nor-

mal. Indeed, in the case of some histograms one can

see that they are bi-modal (e.g., Figure 2). To pro-

vide more reliable evidence we performed normality

tests for ten most numerous digraphs. We used two

We believe that language does not affect the type of dis-

tribution and only parameters can be changed, provided that

this is a native-language of the typist (compare (Bergadano

et al., 2002)).

Figure 2: Distribution of ﬂight time timing for digraph "IE".

tests: Lilliefors test (Lilliefors, 1967) and Shapiro -

Wilk (Shapiro and Wilk, 1965) The level of signiﬁ-

cance is set to α = 0.05 (statistically signiﬁcant). The

null hypothesis H

- ﬂight time timings are normally

distributed is tested.

Table 2: Normality tests for some digraphs.

Graph Amount Test (p-val) Test (p-val) Rejection

of probes Shapiro- Lilliefors H

Wilk

ie 542 < 2.2e-16 < 2.2e-16 YES

e_ 501 < 2.2e-16 < 2.2e-16 YES

a_ 438 < 2.2e-16 < 2.2e-16 YES

ni 426 < 2.2e-16 < 2.2e-16 YES

_p 332 < 2.2e-16 < 2.2e-16 YES

ow 284 < 2.2e-16 < 2.2e-16 YES

” 273 < 2.2e-16 < 2.2e-16 YES

ze 271 < 2.2e-16 < 2.2e-16 YES

o_ 259 < 2.2e-16 < 2.2e-16 YES

po 256 < 2.2e-16 < 2.2e-16 YES

wa 170 < 2.2e-16 < 2.2e-16 YES

do 152 < 2.2e-16 < 2.2e-16 YES

ad 100 5.612e-15 < 2.2e-16 YES

io 64 8.741e-11 1.262e-14 YES

el 50 1.097e-08 3.228e-11 YES

Results presented in Table 2 allow us to safely reject

the hypothesis about normality of digraphs timings.

3.2 n-Graphs Approach

In the paper (Sim and Janakiraman, 2007) one can

ﬁnd a very important observation – the distribution

of digraph ﬂight times depends on their contexts (key

pressed before and after the digraph) and the longer

context is the more the shape of the histogram resem-

bles Gaussian distribution. In other words, this means

that n-graphs for n ≥ 3 should have distribution closer

to Gaussian.

In Fig. 3 a histogram for ie digraph is disunited in

histograms of contributing trigraphs.

Let us investigate Fig. 3. We can observe two

peaks: ﬁrst over 100ms and the second around 250ms.

SECRYPT2012-InternationalConferenceonSecurityandCryptography

298

Figure 3: Distribution of ﬂight time timing for trigraphs in-

cluded in the digraph "IE".

One can conjecture that in general the distribution of

timings of a digraph xy would be a combination

some other, basic unimodal distributions deﬁned as

follows:

∑

pre,post

pre||xy||post

1[Preﬁx = pre,Postﬁx= post]

Where Y

are from the same family of distribution,

however with different parameters depending on indi-

vidual user and particular string a. Note that 1[W] de-

notes an indicator function, i.e., it is equal 1 if asser-

tion W is true, otherwise it is 0. Such approach would

be coherent with observation from (Sim and Janakira-

man, 2007) and seems to be, at least to some extent,

justiﬁed. Indeed, typing a digraph for a ﬁxed context

can be treated as an experiment that is repeated under

the same conditions. In such model close approxima-

tion of X can take into account only preﬁxes of length

1 - i.e., trigraphs.

It is not not clear, however, if Y

for different a’s

are Gaussian, at least for short context. One can ob-

serve that histograms of trigraphs have high skewness

that suggests that normal distribution is very unlikely.

Initial analysis suggests that this may be Lognormal,

Beta or Burr distribution, though due the small size of

dataset these experiments could not be very reliable.

We performed some tests and obtained following re-

sults given in Table 3.

Presented results are ambiguous – we cannot def-

initely reject any hypothesis about real distribution of

This is not a mixture of distribution.

Table 3: Normality tests for some trigraphs.

Graph Amount Test (p-val)Test (p-val)Rejection

of probes Shapiro- Lilliefors H

Wilk

nie 137 < 2.2e-16 < 2.2e-16 YES

wie 26 1.059e-06 0.0001074 YES

sie 44 2.354e-09 1.440e-09 YES

pre 51 0.06108 0.02186 NO

cji 42 0.9153 0.9535 NO

Table 4: Occurrence of all trigraphs forming the space of

"?IE".

Trigraph EIE BIE ZIE PIE KIE

Occurrence[%] 0.89 2.37 4.45 5.64 6.53

Trigraph MIE WIE CIE SIE NIE

Occurrence[%] 6.53 7.72 11.57 13.06 40.65

trigraphs since collected dataset is too small. Investi-

gating this problem as well as testing the conjecture

about the distribution remains future work.

Beyond n-Graphs. We believe that there is many

other data that can be used for recognizing particular

typist. One example is frequency of some character-

istic mistakes. Another rich source of information is

the usage of SHIFT key with digraphs containing a

key of double meaning (e.g. : / ; or " / ’).

Due to space limitation we do not present experimen-

tal results.

4 EFFECTIVE

COUNTERMEASURES

In this section we present methods that can, to some

extent, protect users from threats pointed out in Sec-

tion 2. The algorithms we present below relay on in-

terception of pressed keys and obfuscating real tim-

ings by injecting artiﬁcial delays. The defense meth-

ods should be planted on a level when modiﬁcation

is possible before the attacker can intercept the data,

though basically they acts similar to keyloggers. We

can think about a hardware device installed on a key-

board’s plug or a special software controlling mes-

sages sent later thorough the network. One may argue

that in many distributed systems some delays occur

as side effects of realizing basic functionalities (e.g.,

SSH2). Nevertheless usually one cannot have any

control when we aim at providing mechanisms that

guarantee provable security.

The most challenging aim in designing security

mechanisms of that kind is to provide high level of

security without affecting signiﬁcantly the usability

of the system. One can easily notice that idea behind

SomeRemarksonKeystrokeDynamics-GlobalSurveillance,RetrievingInformationandSimpleCountermeasures

299

our protocols leads to lags in communication, that can

signiﬁcantly lower responsiveness of the system and

be unacceptable for users. This pertains in particular

to users working in an interactive mode.

All methods described below use a kind of buffer

and require access to precise time. Pressed keys are

stored in the buffer and are released with some pre-

cisely assigned delay, thus every key in the buffer

needs to have a special auxiliary data (a timestamp)

when the key was put into the buffer. Of course size

of the buffer should be possibly small. Nevertheless

limiting the size of the buffer is much less important

than limiting the delay.

4.1 Threshold-constant Time Delays

Method

The most obvious defense strategy is to withhold

sending keys so that all ﬂight times would be per-

ceived as constant that is equal the longest observable

ﬂight time over all digraphs. Such an approach cannot

be implemented directly, since in some cases Flight

Times can be extremely long (e.g., pause in typing).

In Algorithm 1 we obfuscate all timings up to a given

threshold. That is, ∆ is the threshold value beyond

which obfuscating ends.

Main Features. The proposed solution is very sim-

ple in implementation and does not require knowl-

edge of distribution of ﬂight times. Moreover

changing the parameter ∆ regulates obfuscation/delay

threshold. Heuristic approach providing high level of

security would be setting ∆ = 800 ms. According to

some data revealed in (Monrose and Rubin, 1997) one

may expect that bulk of all digraphs fall to “obfus-

cated interval”. On the other hand, ﬂight time of most

common in our data digraph ’IE’ is slightly larger

than 100ms, and other common digraphs have ﬂight

time around 200ms. Thus the time of inserting the

message can be over 4 times longer. Moreover basic

observations of queuing theory suggests that one can

expect the required size of the buffer up to size equal

to the length of the input text. On the other hand, this

method provides very strong level of security - indeed

- most timings are totally obfuscated and the picture

seen by the adversary is oblivious. In effect, the ad-

versary gets no knowledge about the typist.

Algorithm 1 works best for consistent typists and

in a scenario where the user types short texts and in-

teraction is needed. It can be also considered for sys-

tems with texts of moderate size where delay is ac-

cepted.

Algorithm 1: Threshold-constant strategy.

Read Key

; Release Key

Read Key

; Release Key

if FlightTime(Key

,Key

) < ∆ then

FlightTime ← ∆

else

FlightTime ← FlightTime(Key

,Key

)

end if

4.2 Pool Buffer Method

For protecting user privacy in typing longer text one

may apply another strategy. Algorithm described in

this section follows two simple rules: gather and

ﬂush. We ensure a large buffer of size n and in ﬁrst

stage of algorithm, when the user types, algorithm

withholds the pressed keys until

slots are ﬁlled.

Starting at that point second stage begins and buffer

outputs stored data in short and constant time inter-

vals (e.g. 5 ms), simultaneously receiving new input

and storing it in the second half of the buffer. Note

that this approach is similar to some kinds of MIX

protocol used for protecting anonymity in communi-

cation (Serjantov and Newman, 2003).

Problem with short texts can be solved by ﬁxing

a time parameter T depicting time period after which

we consider typing as completed. One solution is as

follows – when time since last key press is longer that

T, buffer, starting from current position up to

, is

ﬁlled with neutral symbol (i.e., NULL) and the proce-

dure continues until all positions from 0 to

contain

only neutral symbols. Of course choice of protocol

parameters n and T depends on particular scenario.

Main Features. One can easily see that security of-

fered by the protocol depends on parameter n. Instead

of timings T

,. .., T

n/2

the adversary obtains only

their sum i.e., S = T

+ .. . + T

n/2

that provides sig-

niﬁcantly less information. Generally security guar-

antees offered by this algorithm are lower than those

offered by algorithm described in 4.1, especially for

small buffer size n. However, this protocol clearly has

some unquestionablemerits - size of the buffer as well

as delay are strictly controllable and limited. More-

over some extremely long ﬂight times are to some ex-

tent hidden. This can be important since very long

timings can provide signiﬁcant information about dis-

tinctive behavior of individuals.

SECRYPT2012-InternationalConferenceonSecurityandCryptography

300

4.3 Masquerade Method

Another approach is to replace the real ﬂight time for

particular digraph XY by a random δ

chosen ran-

domly from some distribution deﬁned for XY. Such

approach not only hides real timings of the user but

also can pretend other individual. Similarly, this ap-

proach can be extended to n-graphs. The method of-

fers moderate delay and requires relatively long size

of the buffer.The main disadvantage is the need of

keeping distribution of the digraphs, which is quite

difﬁcult as shown in Section 3.

5 CONCLUSIONS

In this paper we discussed several issues related to

keystroking biometric techniques. We pointed out

some potential risks with particular focus on privacy

threat as well as some simple countermeasures. We

believethat issues related to this area are generally un-

derestimated. In effect many fundamental questions –

theoretical as well as practical are left unanswered. In

particular there is no convincing and possibly exact

statistical model of timings of n-graphs. It is also not

clear which other information (e.g., mistakes in typ-

ing ) can be used for recognizing individuals.

We also see the need of providing much more ex-

perimental results about statistics that appear in our

paper. The volume of data we used allows us to test

only a few simple hypothesis e.g., about normality of

distribution of digraphs. With this respect, this pa-

per is a preliminary work revealing only a fraction of

problems in the area of proﬁling based on keystroke

dynamics.

REFERENCES

Bergadano, F., Gunetti, D., and Picardi, C. (2002). User au-

thentication through keystroke dynamics. ACM Trans.

Inf. Syst. Secur., 5(4):367–397.

BioPassword Inc. (2007). Authentication Solutions

Through Keystroke Dynamics. Technical report.

Cho, S. and Hwang, S. (2006). Artiﬁcial rhythms and

cues for keystroke dynamics based authentication. In

(Zhang and Jain, 2006), pages 626–632.

Chudá, D. and Durﬁna, M. (2009). Multifactor authentica-

tion based on keystroke dynamics. In Rachev, B. and

Smrikarov, A., editors, CompSysTech, page 89. ACM.

Gaines, R. S., Lisowski, W., Press, S. J., and Shapiro, N.

(1980). Authentication by keystroke timing: Some

preliminary results. Technical report, RAND Corpo-

ration.

Joyce, R. and Gupta, G. K. (1990). Identity authentica-

tion based on keystroke latencies. Commun. ACM,

33(2):168–176.

Lilliefors, H. W. (1967). On the kolmogorov-smirnov

test for normality with mean and variance un-

known. Journal of the American Statistical Associ-

ation, 62(318):399–402.

Monrose, F. and Rubin, A. D. (1997). Authentication via

keystroke dynamics. In Graveman, R., Janson, P. A.,

Neumann, C., and Gong, L., editors, ACM Conference

on Computer and Communications Security, pages

48–56. ACM.

Revett, K. (2009). A bioinformatics based approach to user

authentication via keystroke dynamics. International

Journal Of Control Automation And Systems, 7(1):7–

15.

Revett, K., Gorunescu, F., Gorunescu, M., Ene, M., de Mag-

alhães, S., and Santos, H. (2007). A machine learning

approach to keystroke dynamics based user authenti-

cation. J. Electronic Security and Digital Forensics,

1(1):55–70.

Serjantov, A. and Newman, R. E. (2003). On the anonymity

of timed pool mixes. In Gritzalis, D., di Vimercati, S.

D. C., Samarati, P., and Katsikas, S. K., editors, SEC,

volume 250 of IFIP Conference Proceedings, pages

427–434. Kluwer.

Shapiro, S. S. and Wilk, M. B. (1965). An analysis

of variance test for normality (complete samples).

Biometrika, 52(3/4):591–611.

Sheng, Y., Phoha, V. V., and Rovnyak, S. M. (2005). A par-

allel decision tree-based method for user authentica-

tion based on keystroke patterns. IEEE Transactions

on Systems, Man, and Cybernetics, Part B, 35(4):826–

833.

Sim, T. and Janakiraman, R. (2007). Are digraphs good

for free-text keystroke dynamics? In CVPR. IEEE

Computer Society.

Song, D. X., Wagner, D., and Tian, X. (2001). Timing anal-

ysis of keystrokes and timing attacks on ssh. In Pro-

ceedings of the 10th conference on USENIX Security

Symposium - Volume 10, pages 25–25, Berkeley, CA,

USA. USENIX Association.

Stefan, D., Shu, X., and Yao, D. D. (2012). Robustness

of keystroke-dynamics based biometrics against syn-

thetic forgeries. Computers & Security, 31(1):109–

121.

Zhang, D. and Jain, A. K., editors (2006). Advances in Bio-

metrics, International Conference, ICB 2006, Hong

Kong, China, January 5-7, 2006, Proceedings, vol-

ume 3832 of Lecture Notes in Computer Science.

Springer.

Zhang, K. and Wang, X. (2009). Peeping tom in the neigh-

borhood: Keystroke eavesdropping on multi-user sys-

tems. In USENIX Security Symposium, pages 17–32.

USENIX Association.

Zhang, S., Janakiraman, R., Sim, T., and Kumar, S. (2006).

Continuous veriﬁcation using multimodal biometrics.

In (Zhang and Jain, 2006), pages 562–570.

SomeRemarksonKeystrokeDynamics-GlobalSurveillance,RetrievingInformationandSimpleCountermeasures

301