Optimisation of Smoothing Parameter of Diffeomorphism Kernel
Estimate for Bounded Random Data
Molka Troudi
1
and Faouzi Ghorbel
2
1
Laboratoire de Traitement du Signal, de l’Image et Reconnaissance des Formes, ENIT,BP 37, 1002, Tunis, Tunisie
2
Laboratoire Cristal, ENSI, Campus Science Universiatire de la Manouba, 2010, La Manouba, Tunisie
Keywords: Diffeomorphisme Kernel Estimate, Plug-in Algorithm, Banwidth.
Abstract: The Diffeomorphism Kernel Density Estimator (DKDE) requires the estimation of an optimal value of the
bandwidth to ensure a reliable pdf estimation of bounded distributions. In this paper, we suggest to approach
the optimal bandwidth value by adapting Plug-in algorithm to DKDE estimator. We will show that the pro-
posal method allows better density estimation in the MISE sense. Otherwise, the Gibbs phenomenon com-
pletely disappears. These results are illustrated by some bounded and semi bounded distributions simula-
tions.
1 INTRODUCTION
It is well known that the estimation of the probabil-
ity density functions (pdf) is an important step in
many applications.
In practice, the application of a best estimator
improves the systems performances. For examples,
the optimal scalar quantification which is based on
the pdf estimates is an important step in Signal and
image coder. The advanced hashing procedure
which is known as an essential task in data basis
indexing gives improvement in its performances
when the pdf of signal or image features are well
estimated. In pattern recognition systems, the appli-
cation of the Bayesian classification rule needs the
determination of the conditional pdf and the mixture
one and so on…. The coder parameters, the used
features in data base index systems or the shape
descriptors could be confined to a bounded or a semi
bounded intervals (Ghorbel et al., 2012). The pdf
estimate of such bounded or semi bounded attributes
which are modeled by a set of random variables,
have some convergence problems in its border val-
ues known by the Gibbs phenomenon. For these
raisons, some authors have recently developed new
non parametric pdf estimate methods taking account
of the data support. The Diffeomorphism kernel
estimate is one of this pdf estimate kinds. In the
present work, we propose an improvement of such
method by optimizing its smoothing parameter value
in the mean of the Mean Integrate Square Error
(MISE).
The kernel method is one of the most popular
non-parametric pdf estimation methods (Parzen,
1962). Nevertheless, the studied random variables
are mostly subject to algebraic constraints (bounded
or semi bounded support) which are not respected by
kernel method. The orthogonal series estimators
studied by Hall (Hall, 1982) represent a first solution
to this problem. Unfortunately, a disadvantage relat-
ed to the Gibbs phenomenon on the bias of these
estimators is generally observed. Saoudi et al. (1994)
(1997) and Ghorbel (2011) proposed a new attrac-
tive method based on the kernel method with an
appropriately chosen regular change of variable.
Indeed, thanks to a regular diffeomorphism, the pdf
is estimated on the natural support of the random
variable.
However, the choice of the bandwidth noted by
h
N
is very important. Several techniques have been
proposed for optimal bandwidth selection for the
usual Kernel Density Estimation (KDE) method
(Jones, Marronl and Seather, 1991) (Bowman and
Azzalini, 1997). We focus in this paper on the plug-
in method (Hall and Marron, 1987) which gives a
good approximation of the optimal bandwidth in the
mean integrated square error (MISE) sense. This
method achieves approximation of the bandwidth h
N
by an iterative approximation of second derivative of
the density f, noted by J( f ). Thus, a sequence of
56
Troudi M. and Ghorbel F..
Optimisation of Smoothing Parameter of Diffeomorphism Kernel Estimate for Bounded Random Data.
DOI: 10.5220/0004073600560061
In Proceedings of the International Conference on Signal Processing and Multimedia Applications and Wireless Information Networks and Systems
(SIGMAP-2012), pages 56-61
ISBN: 978-989-8565-25-9
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

positive numbers
()
k
N
h is constructed through the
iterations with N as the sample size, and k as the
number of iterations. Yet, we propose to adjust the
plug-in method to the modified KDE method in
order to obtain a better approximation.
The present paper is organized as follows. Sec-
tion 2 is devoted to recall the Kernel pdf estimate
method. In Section 3, the theoretical principles of
the modified KDE which is adapted to the probabil-
ity density functions with a bounded support are
presented. The convergence according to mean
square error criterion gives a sufficient condition so
that the estimator converges in terms of the integrat-
ed mean square error (IMSE). An asymptotic study
is developed in section 4. So, the expression of the
optimal smoothing parameter is presented according
to IMSE criterion. In section 5, we describe the
different steps of the iterative plug-in algorithm
witch converges to the optimal smoothing parameter
or bandwidth. Therefore, section 6 is devoted to
present some simulations in order to evaluate the
performances of the suggested method.
2 KERNEL PDF ESTIMATE
METHOD
The Kernel pdf Estimate is defined by:
()
1
1
ˆ
N
i
N
i
NN
x
X
fx K
Nh h
=
⎛⎞
−
=
⎜⎟
⎝⎠
∑
(1)
where
(
)
1
i
in
X
≤≤
is the observed data with length
equal to n. h
N
is called the bandwidth and K is a
probability density function called the Kernel. K is
assumed to be an even regular function with unit
variance and zero mean. The evaluation of the per-
formances of estimates methods is usually based on
a measure of distance between the true density f and
its estimate
ˆ
N
f
. Especially common choices are the
Integrated Square Error (ISE) and its expected value,
the Mean Integrated Square Error (MISE).
()
() ()
2
2
ˆˆ ˆ
(, ) ,
NN N
I
SE f f D f f f x f x dx
+∞
−∞
==−
∫
()
() ()
2
ˆˆ
,
NN
M
ISE E ISE f f E f x f x dx
+∞
−∞
⎡⎤
⎡⎤
==−
⎢⎥
⎢⎥
⎣⎦
⎣⎦
∫
The minimisation of MISE with respect to the
bandwidth, for a fixed size N of the sample, implies
the following asymptotic study.
Let us consider the expression of Mean Square Error
(MSE):
()
(
)
2
2
ˆˆˆ
var
NNN
MSE E f f f f E f
⎡⎤
⎡⎤
=−= +−
⎢⎥
⎣⎦
⎣⎦
The development of this expression gives the fol-
lowing formula
() ( )
() ( )
()
()( )
()
2
2
2
2
1
ˆ
1
NN
N
N
N
Ef f Kufxhudu
Nh
Ku f x uh f du
Kuf x hudu
N
⎡⎤
−= −
⎢⎥
⎣⎦
⎡⎤
+−−
⎣⎦
−−
∫
∫
∫
Firstly, let us consider the Taylor pdf expansion:
()() () ()
()
()
2
2
33
3
'"
2
6
NNN
N
N
u
f
xhu fx huf x hf x
uh
fxhu
θ
−
=− + −
−
where 0 < θ < 1.
By using the following notations:
() ()
2
M
KKudu
+∞
−∞
=
∫
(2)
and
() ()
(
)
2
"
J
ffxdx
+∞
−∞
=
∫
(3)
where f " is the second derivative of f.
Δ(hN), which is the Taylor expansion of the
MISE (and consequently an approximation of
MISE) is given by:
()
() ()
4
4
N
N
N
M
KJfh
MISE h
nh
≈Δ = +
The minimum value of the function
()
N
hΔ
is ob-
tained by annulling its derivative
'( ) 0
N
hΔ=.
()
3
2
()
'()0
NN
N
MK
hhJf
nh
Δ
=− + =
Therefore, the optimal value of h
N
noted by
*
N
h
be-
comes:
()
()
()
()
1
11
*
5
55
..
N
hn Jf MK
−
−
=
(4)
This minimum value of the MISE is given by the
following expression:
OptimisationofSmoothingParameterofDiffeomorphismKernelEstimateforBoundedRandomData
57

()
()
()
()
4
5
41
55
5
4
M
ISE N M K J f
−
=
(5)
3 DIFFEOMORPHISM KERNEL
PDF ESTIMATE METHOD
The Diffomorphism Kernel Density Estimation
method (DKDE) (Saoudi et al., 1994) (Saoudi et al.,
1997); (Ghorbel, 2011) is based on appropriately
chosen regular change of variable. Let [X
1
,
X
2
,….,X
N
] be N observations of random variable X
and φ a C1-difféomorphism from ]a , b[ to R. The
following estimator:
()
()
() ( )
1
'
ˆ
N
i
N
i
NN
x
xX
fx K
Nh h
φ
φφ
=
−
⎛⎞
=
⎜⎟
⎝⎠
∑
(6)
is asymptotically unbiased when h
N
tends towards 0
and φ’(x) tends towards infinity when x tends to-
wards a or b which are the bounds of the interval ]a,
b[. The expectation of the suggested estimator is
estimated by:
()
()
() ( )
1
'
ˆ
N
i
N
i
NN
x
xX
Ef x EK
Nh h
φ
φφ
=
⎡⎤
−
⎛⎞
⎡⎤
=
⎢⎥
⎜⎟
⎣⎦
⎢⎥
⎝⎠
⎣⎦
∑
Using the following change of variable,
(
)
(
)
N
x
u
y
h
φφ −
=
the expression of variance be-
comes:
() ()
() ()
()
()
()
()
()
2
'
11
,
ˆ
'
N
N
N
xyh
R
gxy
Ef x x
K
y fo x uh dy
φ
φ
φφ φ
−−
−
⎡⎤
=
⎣⎦
−
∫
144444424444443
Let us compute the variance of this estimator by
using the same change of variable:
()
()
() ()
()
()
()
()
()
()
{}
2
'
21 1
,
2
'
ˆ
var
1
ˆ
N
N
N
N
xyh
R
gxy
N
x
fx
Nh
K
y fo x uh dy
Ef x
N
φ
φ
φφ φ
−−
−
⎡⎤
=
⎣⎦
−
⎡⎤
−
⎣⎦
∫
144444424444443
The mean square error (MSE) is
() () () ()
{}
() () ()
2
2
2
ˆˆˆ
var
ˆ
2
NNN
N
Ef x fx f x Ef x
fxEf x f x
−= +
−+
⎡⎤
⎡
⎤⎡ ⎤
⎣
⎦⎣ ⎦
⎢⎥
⎣⎦
⎡⎤
⎣⎦
The MSE becomes:
() ()
()
()( ) ()( )
() ()
()()
()
{}
2
2
2
2
2
ˆ
'
,,
',
N
N
N
RR
N
R
Ef x fx
x
K ygxydyh Kygxydy
Nh
Ky xg xy fx dy
φ
φ
−=
−
+−
⎡⎤
⎢⎥
⎣⎦
⎧
⎫
⎡⎤
⎪
⎪
⎢⎥
⎨
⎬
⎢⎥
⎪
⎪
⎣⎦
⎩⎭
∫∫
∫
As (φ-1)’is bounded on R, f is assumed to be bound-
ed on ]a, b[ and K2 is integrable on R, the Lebesque
convergence theorem can be easily applied, then the
MSE, for a large value of N, becomes equivalent to:
() ()
(
)
(
)
()
()
()
2
2
2
'
ˆ
N
N
R
N
xfx
E
fx fx Kydy
Nh
fx
oh
N
φ
−=
−+
⎡⎤
⎢⎥
⎣⎦
∫
Because of the continuity of φ ’ on R and f on ]a, b[,
this estimator converges in IMSE for all compact of
]a, b[. To obtain this convergence according to the
IMSE criterion, the function
φ ’(f) have to be inte-
grable on ]a, b[ because:
() ()
() () ()
() ( ) ()
2
2
2
ˆ
1
'
1
b
N
a
b
a
N
R
b
N
a
Ef x fx dx
f
xxdxKydy
Nh
f xdx b aoh
N
φ
⎡⎤
−=
⎢⎥
⎣⎦
−+−
∫
∫∫
∫
Saoudi and al. (Saoudi et al., 1994) shows that the
logarithmic diffeomorphism allows a better conver-
gence of the estimator.
]
[
,
:,
ab
ab R
x
a
xLog
bx
φ →
−
⎛⎞
→
⎜⎟
−
⎝⎠
4 ASYMPTOTIC STUDY
The quality of the pdf estimation depends on the
choice of the optimal smoothing parameter or band-
width h
N
. The MSE expression can be written as
following:
SIGMAP2012-InternationalConferenceonSignalProcessingandMultimediaApplications
58

() () () () ()
2
ˆ
NNN
N
E
fxfx AxBxCx−=+−
⎡⎤
⎣⎦
With
()
()
()( )
2
2
'
,
N
R
N
x
A
xKygxydy
Nh
φ
=
∫
() () ()()
2
',
N
R
Bx Ky gxy fxdy φ =−
⎧⎫
⎢⎥
⎨⎬
⎣⎦
⎩⎭
∫
()
()
()( )
2
2
'
,
N
R
x
Cx Kygxydy
N
φ
=
⎧⎫
⎨⎬
⎩⎭
∫
We consider Taylor expansion of the function Hy
defined as following in the neighborhood of
φ (x):
() ()
(
)
()
()
(
)
11
'
y
H
NN
x
fo x yh x yh φφφφφ
−−
−−⎯⎯→
It implies that there exists a positive number θ less
than 1 such that:
()
()
()
(
)
()
()
()
()
()
()
'
22 33
'' '''
26
yNy Ny
NN
yyN
H x yh H x yh H x
yh yh
Hx Hxyh
φφφ
φφθ
−= −
+−−
The following approximations are deduced from the
computation of the successive derivatives of the
function Hy in
φ (x):
()
()
()
()
'
N
N
xfx
A
xMK
Nh
φ
≈
()
()
[]
()
4
2
8
4'
N
N
h
B
xFx
x
φ
=
()
()
[]
N
xf
xC
N
2
=
with
() () () () ()
() () () () ()
[]
2
2
3 '' ' '''
3' ' '' '' '
Fx f x x x x
fx x x f x x
φφφ
φφ φ
=−
−+
⎡⎤
⎡⎤
⎣⎦
⎣⎦
(7)
The asymptotical study of IMSE gives:
()
() () ()
[]
()
() ()
()
()
[]
2
4
2
8
ˆ
,
'
4
'
NNNN
R
N
RR
N
D
ff Ax Bx Cxdx
h
MK F x
x
f x dx dx
Nh
x
φ
φ
=+−
≈+
∫
∫∫
If
M
φ
and
J
φ
exists, we have:
() () () ()
'
R
M
KMK xfxdx
φ
φ =
∫
(8)
and
()
(
)
()
[]
2
8
'
R
Fx
J
fdx
x
φ
φ
=
∫
(9)
The optimal value of h
N
noted by
*
N
h
can be de-
duced by minimization of IMSE.
() ()
111
*
555
N
hMK Jf N
φφ
−−
⎡⎤⎡⎤
=
⎣⎦⎣⎦
(10)
5 PLUG-IN DIFFEOMORPHISM
KERNEL ESTIMATE
ALGORITHM
Several methods are proposed in the literature for
selecting optimal bandwidth parameter. The best
known of these include rules of thumb, oversmooth-
ing, least squares cross-validation, direct plug-in
methods, solve-the-equation plug-in method, and the
smoothed bootstrap (Jones et al., 1991); (Bowman
and Azzalini, 1997); (Hall and Marron, 1987). We
focus in this paper on the direct plug-in method
applied to the kernel diffeomorphism application.
Such a method is an iterative algorithm which con-
verges to the optimal bandwidth.
Following, let’s recall the steps of the plug-in al-
gorithm.
Step 1: Arbitrary initialization of
(
)
M
K
φ
. For the
experimentations of section 6, we chose to give to
(
)
M
K
φ
, the M(K) value according to equation (2).
Step 2: Arbitrary initialization of
(
)
(0)
J
f
φ
in order to
determinate
()
0
N
h (equation (10)).
Step 3: Estimation of the pdf
()
0
f
using
()
0
N
h and
equation (6).
Step 4: At the k
th
iteration, estimation of
(
)
M
K
φ
(equation (8)),
()
(
)
'
k
f
and
()
(
)
"
k
f
.
Step 5: Estimation of
()
(
)
k
Jf
φ
(equation (9)) and
deduction of
()
k
N
h (equation (10)).
Step 6: Estimation of
(
)
k
f
(equation (6)).
Step 7: Stopping the algorithm is conditional on a
low relative difference betwee
()
k
N
h and
()
1k
N
h
−
(less
than 1%).
OptimisationofSmoothingParameterofDiffeomorphismKernelEstimateforBoundedRandomData
59

6 PLUG-IN DIFFEOMORPHISM
KERNEL ESTIMATE
PERFORMANCES
In this section, we intend to compare the plug-in
kernel diffeomorphism pdf estimator with the fast
plug-in kernel pdf estimator which have been pub-
lished in a previous work (Troudi et al., 2008).
Three distributions are estimated: an exponential
distribution (E(X) =1) which is semi bounded and
defined on R+, a beta distribution (parameters =
(2,2)) which is bounded and defined on [0, 1] and an
uniform distribution defined on [0, 0.1].
6.1 Exponential Distribution
The estimation of the beta pdf by plug-in kernel pdf
estimator (KDE) is presented in figure 1. Figure 2
represents this estimation by the plug-in dif-
feomorphism kernel pdf estimator (DKDE) which
allows obviously a better estimation with an im-
portant reduction of Gibbs phenomenon. These re-
sults are corroborated by MISE values which are
presented in table 1.
6.2 Beta Distribution
Figures 3 and 4 shows that the estimation of beta
distribution pdf by the plug-in diffeomorphism ker-
nel pdf estimator gives better results than those ob-
tained by usual plug-in kernel pdf estimator. The
Gibbs phenomenon is eliminated and the smoothing
seems to be better. The MISE values versus the
sample size presented in table 1 confirm these ob-
servations.
Table 1: MISE values versus sample size.
MISE for exponential pdf
Sample size Plug-in KDE Plug-in DKDE
1000 3.79*10-5 7.76*10-6
2000 2.68*10-5 6.01*10-6
3000 2.00*10-5 5.51*10-6
4000 9.06*10-6 3.13*10-6
5000 7.80*10-6 2.81*10-6
MISE for beta pdf
Sample size Plug-in KDE Plug-in DKDE
1000 0.0080 0.0058
2000 0.0044 0.0036
3000 0.0033 0.0027
4000 0.0024 0.0022
5000 0.0019 0.0018
MISE for uniform pdf
Sample size Plug-in KDE Plug-in DKDE
1000 0.2502 0.1457
2000 0.1903 0.0746
3000 0.1651 0.0561
4000 0.1546 0.0445
5000 0.1451 0.0359
6.3 Uniform Distribution
The uniform distribution is known by its difficulties
to be estimated. The Plug-in Diffeomorphism Kernel
pdf estimate gives better results than the convention-
al Plug-in Kernel pdf estimate as it’s shown in fig-
ures 5 and 6. Although the uniform distribution is
well known by its difficulties in estimating, the
DKDE method allows a better MISE values as is
shown in table 1.
Figure 1: Pdf estimation of an exponential distribution by
Plug-in Kernel Density estimator (KDE).
Figure 2: Pdf estimation of an exponential distribution by
Plug-in Diffeomorphism Kernel Density Estimator
(DKDE).
Figure 3: Pdf estimation of a beta distribution by Plug-in
Kernel Density estimator (KDE).
-2 -1 0 1 2 3 4 5 6 7 8
0
0.2
0.4
0.6
0.8
1
Plug-in kernel pdf estimator
f
f estimated
-2 -1 0 1 2 3 4 5 6 7 8
0
0.2
0.4
0.6
0.8
1
Plug-in diffeomorphism kernel pdf estimator
f
f estimated
-0.4 -0.2 0 0.2 0.4 0.6 0.8 1 1.2 1.4
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
Plug-in kernel pdf estimato
r
f
f est im ated
SIGMAP2012-InternationalConferenceonSignalProcessingandMultimediaApplications
60

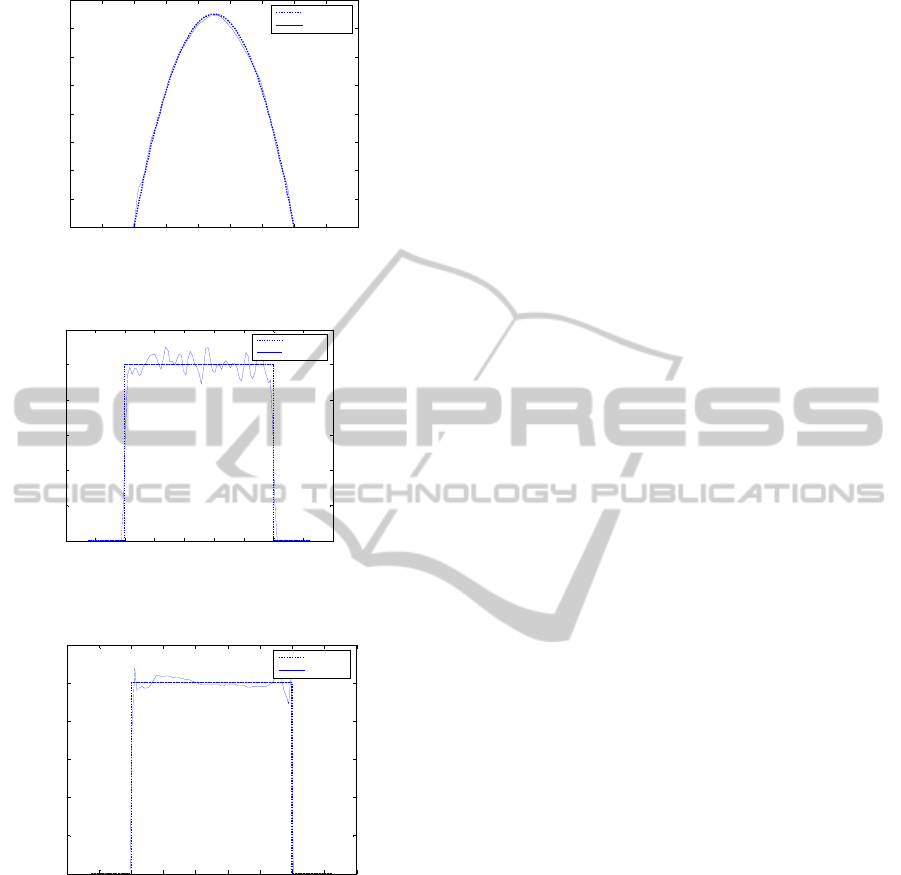
Figure 4: Pdf estimation of a beta distribution by Plug-in
Diffeomorphism Kernel Density estimator (DKDE).
Figure 5: Pdf estimation of a uniform distribution by Plug-
in Kernel Density estimator (KDE).
Figure 6: Pdf estimation of an exponential distribution by
Plug-in Diffeomorphism Kernel Density Estimator
(DKDE).
7 CONCLUSIONS
In this work, we have generalized the plug-in algo-
rithm which adjusts the smoothing parameter of the
kernel pdf estimate, to the diffeomorphism kernel
estimate version. Such modified plug-in algorithm
comes from the optimization of the MISE of this
estimate. This generalization gives a more compli-
cated iterative algorithm since the values of two
parameters depending on the unknown pdf have to
be approximated along iterations instead of only one
parameter on the classical plug-in. It is important to
note that the convergence is obtained for the pro-
posed algorithm. By simulations concerning differ-
ent kinds of distributions confined to bounded or
semi bounded supports, we illustrate the better per-
formance of the proposed Plug-in Diffeomorphism
Kernel pdf estimate in the sense of MISE.
In our future works, we intend to study the case
of multivariate bounded support distributions. We
also test this well performance estimate in real data.
REFERENCES
Ghorbel, F., Derrode, S., Alata, O., 2012. Récentes avan-
cées en reconnaissance de forme statistique. Arts-Pi
editions, Tunis.
Parzen, E., 1962. On estimation of a probability density
function and mode. Annals of mathematical statistics,
33, pp. 1065-1076.
Hall, P., (1982). Comparison of two orthogonal series
methods of estimating a density and its derivatives on
interval. J. Multivariate anal., 12, pp. 432 – 449.
Saoudi, S., Ghorbel, F., Hillion, A., (1994). Non paramet-
ric probability density function estimation on a bound-
ed support: applications to shape classification and
speech coding. Applied Stochastic Models and Data
Analysis, 10, pp. 215-231.
Saoudi, S., Ghorbel, F., Hillion, A., (1997). Some statisti-
cal properties of the Kernel-diffeomorphism estimator.
Applied Stochastic Models and Data Analysis,10, pp.
39-58.
Ghorbel, F., (2011). Vers une approche mathématique
unifiée des aspects géométriques et statistiques de la
reconnaissance de formes planes. Arts-Pi éditions,
Tunis, 2
d
edition.
Jones, M. C., Marron, J. S., Seather, S. J., (1996). A brief
survey of bandwidth selection for density estimation.
J. Amer. Stat. Assoc., 91, pp. 401 – 407
Bowman, A.W., Azzalini, A.,(1997). Applied Smoothing
Techniques for Data Analysis. Oxford University
Press.
Hall, P., Marron, J. S., (1987). Estimation of integrated
squared density derivatives. Statistics &Probability
letters, 6, pp. 109 – 115.
Troudi, M., Alimi, A. M., Saoudi, S., (2008). Analytical
Plug-in Method for Kernel Density Estimator Applied
to Genetic Neutrality Study. Eurasip Journal of ad-
vances in Signal Processing (Eurasip-JASP), 2008,
Article ID 739082, 8 pages doi: 10.1155/2008/739082.
-0.4 -0.2 0 0.2 0.4 0.6 0.8 1 1.2 1.4
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
Plug-in diffeomorphism kernel pdf estimator
f
f estimated
-0.04 -0.02 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14
0
2
4
6
8
10
12
Plug-in Kernel pdf estimate
f
f es timated
-0.04 -0.02 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14
0
2
4
6
8
10
12
Plug-in Diffeomorphism Kernel pdf estimate
f
f estimate
OptimisationofSmoothingParameterofDiffeomorphismKernelEstimateforBoundedRandomData
61