The Concept of Compatibility between Identity-based and Certificateless
Encryption Schemes
Antigoni Polychroniadou
1
, Konstantinos Chalkias
2
and George Stepanides
2
1
Royal Holloway, University of London, Egham, Surrey TW20 0EX, U.K.
2
University of Macedonia, Egnatia 156, 54006, Thessaloniki, Greece
Keywords:
Compatibility, Identity-based Encryption, Certificateless Encryption, Protocol Classification, Efficiency
Comparison.
Abstract:
This paper introduces the concept of compatibility and presents an extended classification of two IBE-related
schemes, the Identity-Based Encryption (IBE) and the Certificate-Less Encryption (CLE) in order to imple-
ment compatible systems. It cannot be denied that IBE, which can be extended to support a plethora of
encryption models, gains widespread adoption day by day as it solves problems within conventional public
key schemes and it results in a simplified key management, making it much more lightweight to deploy. Based
on the fact that a number of different encryption schemes stemmed from IBE, an implementation of an IBE-
related compatible system enables a number of different encryptions on-the-fly based on the user’s needs at
a specific moment. Our approach categorizes known concrete constructions from two IBE-related types into
classes and analyzes similarities concerning public settings, used keys, protocol structures and provided model
of provable security. Therefore, we consider compatibility issues between CLE and IBE and we conclude that
a significant number of them are closely related. Therefore, the concept of compatibility can be put into
practice.
1 INTRODUCTION
Traditional RSA (or similar) encryption is still con-
sidered the first option for e-commerce transactions
and key exchange. This is based on the fact that cur-
rent security infrastructure in the web is mainly based
on RSA digital certificates. On the other hand, ellip-
tic curve cryptography (ECC) is considered to offer
the same level of security with RSA but with smaller
key-sizes. Unfortunately,although ECC has been pro-
posed years ago as an RSA alternative, currently, ECC
is mostly used in constrained devices and thus ac-
tual web transactions are mostly based on RSA en-
cryption and signatures. Moreover, there is no doubt
that for a new product or an idea to be applied in the
real world, compatibility with already established ap-
proaches plays the most important role, as history has
shown in the case of passing from DES to 3DES (be-
fore moving to AES) for backward compatibility rea-
sons. Therefore, we issue the compatibility between
schemes stemmed from ECC such as the flexible as
well as the versatile IBE schemes.
To circumvent some of the problems of conven-
tional asymmetric encryption, including the complex-
ity and the maintenance cost arised from the use of
digital certificates, the concept of IBE was proposed
by Shamir (Shamir, 1985) in 1984. However, it took
almost twenty years for an IBE scheme to be proposed
by Boneh and Franklin (Boneh and Franklin, 2003)
in 2001. Since then, a couple of breakthroughs have
been achieved leading to new asymmetric encryption
schemes and applications. Undoubtedly, IBE gains
widespread adoption day by day as it solves problems
within conventional public key schemes based on the
fact that it results in simplified key management,mak-
ing it much more lightweight to deploy. IBE can be
extended to support a plethora of encryption models
and applications including Hirerachical IBE (HIBE),
Certificateless Encryption (CLE) (Al-riyami and Pa-
terson, 2003), Certificate-Based Encryption (CBE),
Fuzzy IBE (FIBE), Timed-Release Encryption (TRE)
to name just a few. Hence, there are numerous the-
oretically efficient IBE-related models in the litera-
ture which offer different advantages and properties.
On the other hand, the commercial use of IBE is not
‘growing’ as fast as someone would expect and we
suppose that both the compatibility issue and the lack
of a complete ECC parameter standardization (includ-
403
Polychroniadou A., Chalkias K. and Stephanides G..
The Concept of Compatibility between Identity-based and Certificateless Encryption Schemes.
DOI: 10.5220/0004076704030407
In Proceedings of the International Conference on Security and Cryptography (SECRYPT-2012), pages 403-407
ISBN: 978-989-8565-24-2
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

ing pairing-friendly curves) are the main reasons hin-
dering the wide use of IBE. The latter is due to the
fact that the most efficient and practical IBE schemes
are currently based on bilinear pairings over elliptic
curve groups for which pairing-friendly elliptic curve
groups have been proposed. The first companies have
already started to exploit IBE commercially. Some
of them are Voltage, Trend Micro, Mitsubishi and
Noretech Microsoft etc. All in all, due to the chal-
lenges that appear in asymmetric encryption, the issue
of moving from one model to another requires much
more attention in order for new schemes, with various
interesting properties, to be widely spread.
From the aforementioned encryption models,
CLE owns some interesting properties making it a
strong candidate to be the ‘connector’ between tradi-
tional public key encryption and IBE. In fact, a CLE
scheme could be characterized as a mixed scheme
which shares properties from both encryption mod-
els, conventional and IBE. As far as CLE and IBE are
concerned, after a thorough research we found that
there are currently at least 35 different concrete IBE
schemes and 30 concrete CLE schemes in the liter-
ature. There are also generic CLE schemes that can
be derived from IBE. Moreover, some of the existing
protocols are independent (Sun et al., 2007), (Cocks,
2001), but some of them share certain features which
allow us to put the concept of compatibility into prac-
tice. So in the following sections, we propose specific
protocols exploring IBE and CLE concepts.
1.1 Classes of IBE
Taking into consideration the similarities, as well as
the differences of numerous IBE proposals, we tried
to organize them into classes. As a result, eight
IBE classes have been modeled in Table 1. Note
that the classes can be generalize into less classes
since Gentry, Sakai-Kashara and BB2 classes belong
to the Exponent-inversion family. Moreover, Waters
and BB1 classes both derive from the commutative-
blinding framework and KW class stems from a full-
domain-hash IBE. We pointed out which of them are
useful or not. The representative scheme of each class
is the first proposed scheme in the literature. There-
fore, the names of the classes derived from the cor-
responding authors’ names of the initial paper for
each approach which does not automatically mean
that these schemes are or are not the best performed
paradigms in their class. This classification depends
on the structure of the keys. Furthermore, we had to
pay attention to the mathematical problems (security
assumptions) on which the security of every scheme
dependson. In Table 1, Msk isthe master secret key of
KGC, Pub is the user’s public key, Priv is the user’s
private key and Gener is a specified generator. The
differences of the keys are obvious.
1.2 Classes of CLE
In an attempt to standardize the closely related CLE
with IBE proposals we classify the CLE schemes into
eight classes. As in the IBE classification, this clas-
sification depends on the structure of the keys and
the security assumptions on which every scheme de-
pends. The eight different classes are depicted in Ta-
ble 2. We emphasize on which of them are useful or
not for comparison and compatibility testing.
1.3 Compatibility
Considering the structure of the keys derived from
CLE classes we set the compatible classes. Table 3
shows the CLE classes corresponding to their IBE
compatible class. By taking into consideration the
competitive and compatible useful classes, the com-
patibility can be put into practice. If the ROM and of
course the Weak-Types of Adversarial Security Mod-
els are considered practically secure, according to
our performance analysis, the SK (Kasahara, 2003)
class has the best efficiency performance, followed
by BB2 and Gentry classes which are proven se-
cure in the standard model. In CLE, among the use-
ful classes, the best performed class is the LQ (Lib-
ert and jacques Quisquater, 2006) class, followed by
AP05 and CCLC classes. The LQ (Libert and jacques
Quisquater, 2006) class is compatible with SK-IBE
class. Depending on their keys and on the security
assumptions they lead to a mixed CLE-IBE system.
Both classes support the simplest implementations. A
drawback of these classes is that the security depends
on a strongest q-BDHI assumption compared to other
classes. We highlight though that our measurements
took under consideration the case of a single KGC,
otherwise some other pairing-based classes could be
benefited from the bilinearity property when multiple
KGCs are to be used. We are currently investigate
the case of multiple KGCs and its effect on the com-
patibility and on the performance of IBE and CLE
schemes. In a multiple KGCs approach, we need to
split the master secret key into additive or polynomial
shares to avoid single points of failure. On the other
hand, a less time efficient commutative blinding BB1
scheme is extremely flexible as well as versatile to im-
plement extensions of IBE followed by BF schemes.
Thus, another mixed CLE-IBE system could be de-
rived from BB1 and CCLC classes sacrificing some of
its efficiency. The combination of BF and AP classes
SECRYPT2012-InternationalConferenceonSecurityandCryptography
404

Table 1: IBE Classes.
IBE CLASSES
BF (Boneh and Franklin, 2003) COCKS (Cocks, 2001) SK (Kasahara, 2003)
KEYS
Msk: s ∈
R
←−Z
q
, P
pub
= sP ∈ G
1
q, p : q ≡ p ≡ 3(mod4) s ∈
R
←−Z
q
, P
pub
= sP ∈ G
1
Pub: ID ∈ {0, 1}
∗
ID ∈ {0, 1}
∗
ID ∈ {0, 1}
∗
Priv: d
ID
= sQ
ID
∈ G
1
r = α
n+5−(p+q)
8
modn ∈ Z
∗
n
d
ID
=
1
s+H
3
(ID)
Q ∈
ˆ
G
1
where where
Q
ID
= H
1
(ID) ∈ G
1
α = H
2
(H
2
(H
2
...(ID))) ∈ Z
∗
n
such that

a
n

= 1,n = pq
where a = ±r
2
modn depending on
whether

a
p

=

a
q

= ±1
Gener: P ∈ G
1
P ∈ G
1
,Q ∈
ˆ
G
1
KW (Katz and Wang, 2003) Waters (Waters, 2005) Gentry (Gentry, 2006)
KEYS
Msk: s ∈
R
←−Z
q
, P
pub
= sP ∈ G
1
s ∈
R
←−Z
q
,sP
2
∈ G
1
s ∈
R
←−Z
q
,P
pub
= sP ∈ G
1
Pub: ID ∈ {0, 1}
∗
ID ∈ {0, 1}
n
ID ∈ Z
q
Priv: d
ID
= (sQ
ID
,b
ID
) d
ID
= (sP
2
· r(u
′
∏
i∈ν
u
i
),rP) d
ID
= (r
i
,h
ID,i
) : i ∈ {1, 2, 3}
where where where
b
ID
∈ {0, 1}, ν ⊆ {1, ..n} where ID
i
= 1 h
ID
=
1
s−ID
(h
i
P
−r
i
) ∈ G
3
1
,
Q
ID
= (H
1
(ID, b
ID
)) ∈ G
1
~
U = (u
i
),u
i
∈
R
←−G
1
, r
i
∈ Z
q
r ∈ Z
q
,u
′
∈ G
1
Gener: P ∈ G
1
P ∈ G
1
P,h1, h2,h3 ∈ G
1
BB1 (Boneh and Boyen,
2004)(a)
BB2 (Boneh and Boyen,
2004)(b)
KEYS
Msk: (Q,α,β, γ) ∈
ˆ
G
1
× ∈ Z
3
q
s
1
,s
2
∈
R
←−Z
q
, P
pub1
= s
1
P,
P
pub2
= s
2
P ∈ G
1
Pub: ID ∈ {0, 1}
∗
ID ∈ Z
q
Priv: d
ID
= (rQ, d
ID
= (r,
1
ID+s
1
+rs
2
Q) ∈
(αβ+ (αH
6
(ID) + γ)r)Q) ∈
ˆ
G
2
1
Z
q
× G
1
where where
r ∈ Z
q
, r ∈ Z
q
Gener: Q ∈
ˆ
G
1
P ∈ G
1
,Q ∈
ˆ
G
1
• The schemes use bilinear map groups (G
1
,G
2
) of prime order q for which there exists a bilinear map
ˆe : G
1
×
ˆ
G
1
→ G
2
satisfying the following properties:
1. Bilinearity: ∀P,Q ∈ G
1
,∀a, b ∈ Z, we have ˆe = (aP, bQ) = ˆe(P, Q)
ab
.
2. Non-degeneracy: ˆe(P,Q) 6= 1 ∈ G
2
.
3. Computability: ∀P, Q ∈ G
1
, the pairing ˆe = (P,Q) can be efficiently computed.
• In addition, type-1 (ˆe : G
1
× G
1
→ G
2
) pairings are symmetric, type-2 (ˆe : G
1
×
ˆ
G
1
→ G
2
) asymmetric pairings
include a one-way mapping from
ˆ
G
1
to G
1
and also there are the type-3 asymmetric pairings in which the groups
are not mapped efficiently to each other.
•The used hash functions are modeled as: H
1
: {0,1}
∗
→ G
∗
1
, H
2
: {0, 1}
∗
→ Z
∗
n
, H
3
: {0,1}
∗
→ Z
∗
q
,
H
4
: {0,1}
∗
× Z
∗
q
→ Z
∗
p
and H
5
: {0,1}
∗
× Z
∗
n
→ Z
odd
n
•We use additive notation for ECC protocols to denote a scalar multiplication
• The RO Model is a security model in which all parties get black-box access to a random function H. The ROM
implies simplicity and practicality in a scheme. However, a security proof in ROM is only a heuristic indication
of the scheme’s security. On the other hand, a model that do not use idealized oracles is the Standard Model in
which the security is proven using only standard complexity assumptions. Thus, a security proof of a scheme in
the standard model is preferred rather than a proof in the ROM.
TheConceptofCompatibilitybetweenIdentity-basedandCertificatelessEncryptionSchemes
405

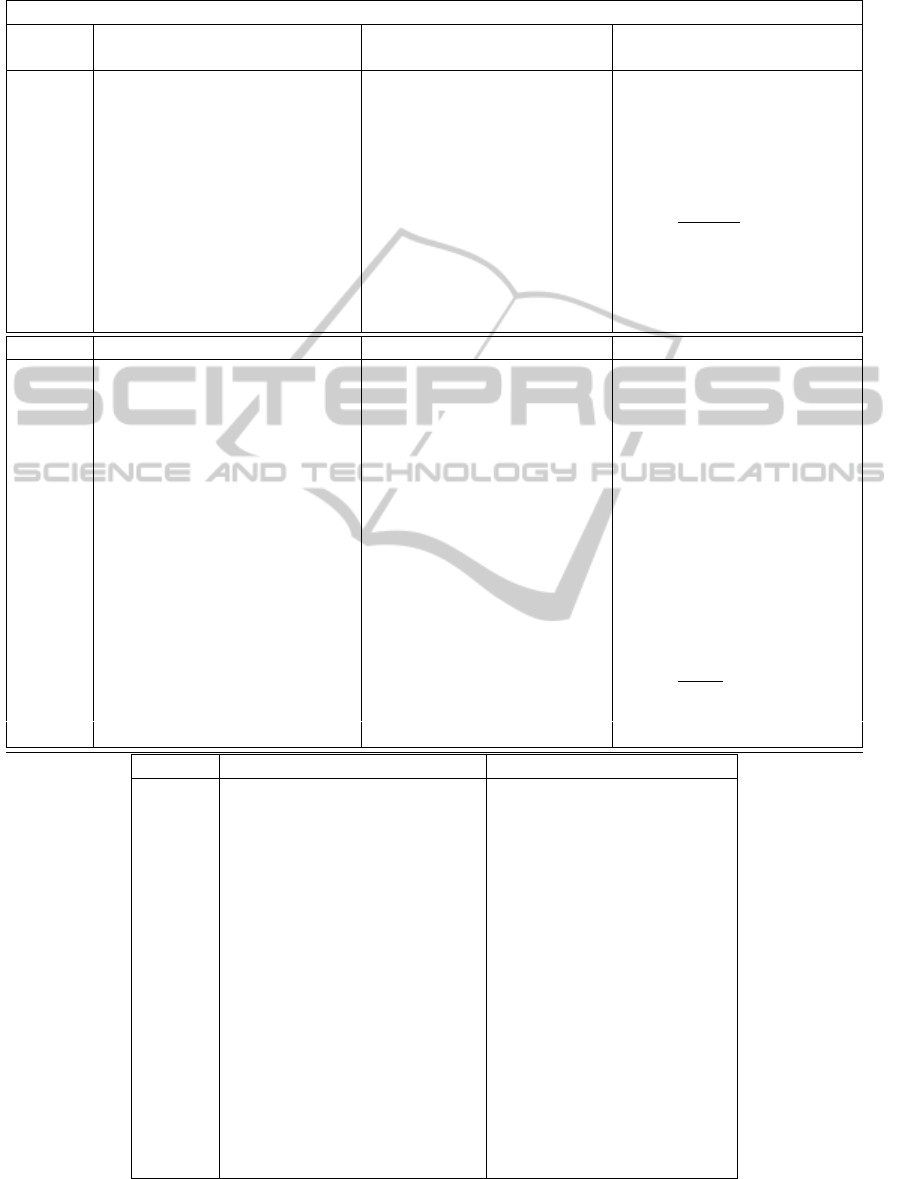
Table 2: CLE Classes.
CLE CLASSES
AP03 (Al-riyami and Pater-
son, 2003)
AP05 (Al-riyami and Pater-
son, 2005)
LQ (Libert and jacques
Quisquater, 2006)
KEYS
Msk: s ∈
R
←−Z
q
, P
pub
= sP ∈ G
1
s ∈
R
←−Z
q
, P
pub
= sP ∈ G
1
s ∈
R
←−Z
q
, P
pub
= sP ∈ G
1
Secret: x ∈ Z
q
x ∈ Z
q
x ∈ Z
q
Pub: P
A
= (X,Y),ID ∈ {0, 1}
∗
P
A
= xP ∈ G
1
,ID ∈ {0,1}
∗
P
A
= g
x
,ID ∈ {0, 1}
∗
where where
X = xP ∈ G
1
,Y = xP
pub
∈ G
1
g = ˆe(P,Q) ∈ G
2
Partial: d
ID
= sQ
ID
∈ G
1
d
ID
= sQ
ID
∈ G
1
d
ID
=
1
H
3
(ID)+s
Q ∈
ˆ
G
1
where where
Q
ID
= H
1
(ID) ∈ G
1
Q
ID
= H
1
(ID) ∈ G
1
Priv: s
ID
= xd
ID
∈ G
1
s
ID
= (d
ID
,x) ∈ G
1
× Z
q
s
ID
= (d
ID
,x) ∈ G
1
× Z
q
Gener: P ∈ G
1
P ∈ G
1
P ∈ G
1
,Q ∈
ˆ
G
1
CCLC (Cheng et al., 2007)(a) BSS (Baek et al., 2005) PCHL (Park et al., 2007)
KEYS
Msk: (Q,α,β, γ) ∈
ˆ
G
1
× ∈ Z
3
q
s ∈
R
←−Z
∗
p
, g
s
∈ Z
∗
q
s ∈
R
←−Z
q
,P
pub
= sP ∈ G
1
h, u
R
←−G
1
Secret: x ∈ Z
q
x ∈ Z
p
x ∈ Z
q
Pub: P
A
= xP ∈ G
1
,ID ∈ {0, 1}
∗
P
A
= (w, u) ∈ Z
∗
q
× Z
∗
q
, P
A
= (X,Y),ID ∈ Z
q
ID ∈ {0, 1}
∗
where where
u = g
x
∈ Z
∗
q
,w = g
a
∈ Z
∗
q
, X = x(P
pub
P
−ID
) ∈ G
1
,
a ∈ Z
∗
p
Y = x· u ∈ G
1
Partial: d
ID
= (rQ, d
ID
= (w, d
0
) ∈ Z
∗
q
× Z
∗
q
d
ID
= (r,h
ID
) ∈ Z
q
× G
1
(αβ + (αH
3
(ID) + γ)r)Q) ∈
ˆ
G
2
1
where where where
r ∈ Z
q
d
0
= a+ sH
4
(ID, w) ∈ Z
∗
q
h
ID
=
1
(s−ID)
(hP
−r
),
Priv: s
ID
= (d
ID
,x) ∈ G
1
× Z
q
s
ID
= (x,d
0
) ∈ Z
∗
p
× Z
∗
q
s
ID
= (x,r, h
ID
)
Gener: P ∈ G
1
,Q ∈
ˆ
G
1
g ∈ Z
∗
p
P ∈ G
1
DLP (Dent et al., 2008) LDLK (Lai et al., 2009)
KEYS
Msk: s ∈
R
←−Z
,
q
sP
2
,P
pub
= sP, d,RsaGroup < p, q, e,d,g >
P
2
∈
R
G
1
Secret: x ∈ Z
q
x ∈ Z
q
Pub: P
A
= (X,Y), ID ∈ {0,1}
n
P
A
= H
2
(ID)
x+d
,
ID ∈ {0, 1}
∗
where
X = xP ∈ G
1
,Y = xP
pub
∈ G
1
,
Partial: d
ID
= (d
0
,d
1
) = d
ID
= H
2
(ID)
d
(sP
2
· rF
u
(ID), rP) ∈ G
1
2
where
F
u
(ID) = u
′
∏
n
i=1
u
ID
i
i
~
U = (u
′
,u
i
),u
i
∈
R
←−G
1
,
r,r
′
∈ Z
q
Priv: s
ID
= (xd
0
· r
′
F
u
(ID), s
ID
= (d
ID
,x) ∈ Z
n
× Z
q
xd
1
· r
′
P)
Gener: P ∈ G
1
SECRYPT2012-InternationalConferenceonSecurityandCryptography
406

Table 3: Compatible Classes.
CLE Classes compatible with IBE Classes
AP03 and AP05 −→ BF
LQ −→ SK
DLP −→ Waters
PCHL −→ Gentry
CCLC −→ BB1
BSS -
LDLK -
- BB2
- COCKS
- KW
are quiet efficient but a practical drawback in terms
of security is their high dependency on random hash
functions. Therefore, based on the fact that the major-
ity of companies that use IBE, such as Voltage, imple-
ment the BF scheme, we constructed compatible sys-
tems companying BF and AP05 compatible classes.
We successfully implemented a compatible scheme in
which users/administrators choose whether they want
to use IBE or CLE on-the-fly.
REFERENCES
Al-riyami, S. S. and Paterson, K. G. (2003). Certificate-
less public key cryptography. In Asiacrypt2003, pages
452–473. Springer-Verlag.
Al-riyami, S. S. and Paterson, K. G. (2005). CBE from CL-
PKE: A generic construction and efficient schemes. In
Public Key Cryptography - PKC 2005, Lecture Notes
in Comput. Sci, pages 398–415. Springer.
Baek, J., Safavi-Naini, R., and Susilo, W. (2005). Certifi-
cateless public key encryption without pairing. In ISC,
pages 134–148.
Boneh, D. and Boyen, X. (2004). Efficient selective-id se-
cure identity based encryption without random ora-
cles. In Proceedings of Eurocrypt 2004, volume 3027
of LNCS, pages 223–238. Springer-Verlag.
Boneh, D. and Franklin, M. (2003). Identity-based encryp-
tion from the weil pairing. SIAM J. of Computing,
32:586–615.
Cheng, Z., Chen, L., Ling, L., and Comley, R. (2007). Gen-
eral and efficient certificateless public key encryption
constructions. In Pairing, pages 83–107.
Cocks, C. (2001). An identity based encryption scheme
based on quadratic residues. In Proceedings of the
8th IMA Int. Conf., pages 360–363. Springer-Verlag.
Dent, A. W., Libert, B., and Paterson, K. G. (2008). Cer-
tificateless encryption schemes strongly secure in the
standard model. In 11th international conference on
Public key cryptography, PKC’08, pages 344–359.
Springer-Verlag.
Gentry, C. (2006). Practical identity-based encryption with-
out random oracles. In EUROCRYPT, pages 445–464.
Kasahara, R. S. M. (2003). ID based cryptosystems with
pairing on elliptic curve. Cryptology ePrint Archive.
Katz, J. and Wang, N. (2003). Efficiency improvements
for signature schemes with tight security reductions.
In Proceedings of the 10th ACM conference on Com-
puter and communications security, CCS ’03, pages
155–164.
Lai, J., Deng, R. H., Liu, S., and Kou, W. (2009). RSA-
Based certificateless public key encryption. In Pro-
ceedings of the 5th International Conference on Infor-
mation Security Practice and Experience, ISPEC ’09,
pages 24–34. Springer-Verlag.
Libert, B. and jacques Quisquater, J. (2006). On con-
structing certificateless cryptosystems from identity
based encryption. In In PKC 2006, pages 474–490.
Springer-Verlag.
Park, J. H., Choi, K. Y., Hwang, J. Y., and Lee, D. H. (2007).
Certificateless public key encryption in the selective-
ID security model (without random oracles). In Pair-
ing, pages 60–82.
Shamir, A. (1985). Identity-based cryptosystems and sig-
nature schemes. In Proceedings of CRYPTO 84 on
Advances in cryptology, pages 47–53. Springer-Verlag
New York, Inc.
Sun, Y., Zhang, F., and Baek, J. (2007). Strongly secure
certificateless public key encryption without pairing.
In CANS, pages 194–208.
Waters, B. (2005). Efficient identity-based encryption with-
out random oracles. In EUROCRYPT 2005, pages
114–127. Springer-Verlag.
TheConceptofCompatibilitybetweenIdentity-basedandCertificatelessEncryptionSchemes
407