Improved Detection of Probe Request Attacks

Using Neural Networks and Genetic Algorithm

Deepthi N. Ratnayake

, Hassan B. Kazemian

and Syed A. Yusuf

Intelligent Systems Research Centre, Faculty of Computing, London Metropolitan University,

166-220 Holloway Road, N7 8DB, London, U.K.

Institute of Industrial Research, University of Portsmouth, PO1 2EG, Portsmouth, U.K.

Keywords: Wlan Security, Probe Request Flooding Attacks, Neural Networks, Genetic Algorithms.

Abstract: The Media Access Control (MAC) layer of the wireless protocol, Institute of Electrical and Electronics

Engineers (IEEE) 802.11, is based on the exchange of request and response messages. Probe Request

Flooding Attacks (PRFA) are devised based on this design flaw to reduce network performance or prevent

legitimate users from accessing network resources. The vulnerability is amplified due to clear beacon, probe

request and probe response frames. The research is to detect PRFA of Wireless Local Area Networks

(WLAN) using a Supervised Feedforward Neural Network (NN). The NN converged outstandingly with

train, valid, test sample percentages 70, 15, 15 and hidden neurons 20. The effectiveness of an Intruder

Detection System depends on its prediction accuracy. This paper presents optimisation of the NN using

Genetic Algorithms (GA). GAs sought to maximise the performance of the model based on Linear

Regression (R) and generated R > 0.95. Novelty of this research lies in the fact that the NN accepts user and

attacker training data captured separately. Hence, security administrators do not have to perform the

painstaking task of manually identifying individual frames for labelling prior training. The GA provides a

reliable NN model and recognises the behaviour of the NN for diverse configurations.

1 INTRODUCTION

Wireless networks are springing up everywhere as it

enables an information-rich environment through

computers and handheld devices with portability and

flexibility, increased productivity, and lower

installation costs. However, the openly exposed

airwave signals, by their nature have increased risks

in security. Wireless Local Area Network (WLAN)

management frames facilitate stations to begin and

maintain connections. In infrastructure WLANs, any

wireless station with a legitimate Media Access

Control (MAC) address can send a probe request

management frame when it needs information from

an Access Point (AP). AP replies to any probe

request with a probe response management frame

with capability information, such as the network

name access point name, supported data rates, etc.

Probe request and response management frames are

open, so the information can be obtained using

freely available sniffing software. Almost all

Wireless Network Interface Cards (NICs) permit

changing their MAC addresses to arbitrary values

through vendor-supplied/open-source drivers or an

application program. Probe Request Flooding

Attacks (PRFA) send a burst of probe requests,

having different source MAC addresses to generate a

heavy workload on the AP which can lead to a

Denial-of-Service (DoS) to its legitimate users.

Vulnerability arising from PRFA can also be

exploited to create other advanced attacks.

In a real WLAN, traffic pattern is usually

unpredictable and also varies on the usage, operating

system and applications used. Further, Wireless

Intrusion Detection System (WIDS) may fail to

capture some of the frames due to network or

environmental issues. Neural Networks (NN)

considered ideal in dealing with real-world tasks,

where data is often messy, uncertain or inconsistent

and perfect solutions may not exist. The capacity to

learn by example makes NNs exceptionally flexible

and powerful as there is no need to create algorithms

to execute a task. The parallel architecture facilitates

high response and computational times. These make

NNs a perfect candidate for application of wireless

attack detection in real world complex environments

345

N. Ratnayake D., B. Kazemian H. and A. Yusuf S..

Improved Detection of Probe Request Attacks - Using Neural Networks and Genetic Algorithm.

DOI: 10.5220/0004077703450350

In Proceedings of the International Conference on Security and Cryptography (SECRYPT-2012), pages 345-350

ISBN: 978-989-8565-24-2

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

(Karygiannis and Owens, 2002); (Landau and

Taylor, 1997); (Ratnayake et al., 2011); (Zhang et

al., 2008)

In a previous empirical study by the authors

(Ratnayake et al., 2011), an external attacker was

identified by analysing the traffic generated from a

user MAC address in a single frequency band of a

WLAN. A supervised feed-forward NN with four

distinct inputs, delta-time, sequence number, signal

strength and frame sub-type is applied to identify

and differentiate a genuine frame from a rogue

frame. The experimental results showed that the use

of NN can detect probe request attacks to a very

high precision.

However, the effectiveness of an Intrusion

Detection System (IDS) is evaluated by its ability to

make correct predictions, and therefore, the NN has

to be optimised and trained. NN optimisation is the

art and science of arranging interconnected factors to

the best possible effect. Many methods are in use

including trial-and-error, which are not rigorous

enough to arrive at a truly optimal structure. In

contrast, Genetic Algorithms (GA) outperform

traditional optimisation methods, due to its

rigorousness in finding optimal parameters. GA is a

search heuristic that is modelled on the principles of

natural selection, reproduction by crossover and

mutation. A fitness function is applied to evaluate

individuals. GA was first used by (Holland, 1975).

(De Jong, 1993) established that population-based

GAs using crossover and mutation could

successfully be applied to optimisation problems in

many areas. Some research work based on GA in the

field of intrusion detection are presented in

(Bankovic et al., 2007); (Gong et al., 2005);

(Haddadi et al., 2010); (Hua and Xiaofeng, 2008);

(Li, 2004); (Pillai et al., 2004); (Wu and Banzhaf,

2010); (Xia et al., 2005); (Yao, 2010). GAs are

frequently successful and considered as the most

popular in real applications (Reeves and Rowe,

2003).

This paper discusses the structural optimisation

component of the NN designed to detect probe

request attacks, using GA. The paper is organised as

follows: Section 2 - Probe request attack detection

using neural networks, Section 3 – Neural network

structure optimisation, Section 4 - Results and

discussion, and Section 5 – Conclusion.

2 PROBE REQUEST ATTACK

DETECTION

A supervised feed-forward NN was designed with 4

input neurons, one hidden layer, with 20 hidden

neurons and a linear output neuron which classifies

genuine frames from rogue frames. The initial

design divided the data sample and used 70% of the

data to train the network and 15% each for

validation and testing respectively. Levenberg-

Marquardt back propagation algorithm was utilised

for training (Ratnayake et al., 2011). The results are

shown in Table 1. Performance of the network was

determined by the overall regression value.

Table 1: Results from the Un-optimised NN.

Training Sample 70% 123640

Validation Sample 15% 26495

Testing Sample 15% 26495

Hidden Neurons 20

Epoch 77

Performance 0.00386

(The Mean Squared Errors (MSEs) of training, validation and

testing were 3.86409e-3, 3.75033e-3 and 3.67129e-3)

Regression (overall) 0.98043

However, NN structural values were 70/15/15

sample sizes and one hidden layer with 20 neurons.

The model’s performance can be misleading due to

over-fitting, which generally occurs when the model

is not evaluated during the NN training. Over-fitted

models do not perform well on unseen data. Cross-

validation is among several methods of estimating

how well a trained model will perform with unseen

data and detect and prevent over-fitting of the model

(Moore, 2001). A 5-fold cross validation test was

performed using the sample data set, and the results

showed that the trained NN will perform

considerably well with unseen data with 73.59 to

100% accuracy rate. However, the intention of this

research is to realise a 100% accurate NN model.

3 NEURAL NETWORK

OPTIMISATION

NN performance can be improved by initialising the

network and training, increasing the number of

hidden neurons and layers, using a different training

function, or using additional training data

(MathWorks, 2012).

This research uses GA approach to optimise the

constructs of NN structure, namely; training,

validation and testing sample percentages, and

number of neurons of the hidden layer. The training

sample contains approximately 175K frames. Larger

numbers of neurons and extra hidden layers give the

NN more flexibility since network has more

SECRYPT2012-InternationalConferenceonSecurityandCryptography

346

Figure 1: The flow diagram of the GA applied.

parameters for optimisation. However, a too large

hidden layer can cause the problem to be under-

characterised and the network must optimise more

parameters than there are data vectors to constrain

these parameters. Further, more neurons and layers

increase processing time, and demands high

processing power (MathWorks, 2012). Therefore, in

this experiment, a single hidden layer and maximum

of 32 hidden neurons were used. A single training

algorithm is selected to train the network. A mix of

MATLAB and Netbeans/JGAP environment were

used to optimise the solution.

(Reeves and Rowe, 2003) state that probably

everybody’s GA is unique. Although, GAs can find

global optima, when it is applied to different

problems, there are other attractors to which they

may converge, with a distance from global

optimality. Since Holland and De Jong, researchers

and practitioners have recommended many

variations of GA recommending population sizes,

initialisation methods, fitness definitions, selection

and replacement strategies, and crossover and

mutation methods. However, Practitioner’s

viewpoint, (Levine, 1997) has a clear and reasonable

deviation from traditional GAs, which this research

utilised as a guideline.

The flow diagram of GA applied is shown in

Figure 1. Population of random chromosomes,

validation, crossover and mutation were performed

in Netbeans Environment. NN training, calculation

of fitness and fitness scaling were performed in

MATLAB environment. The algorithm ran 3 times

with different selection and mutation configurations.

Population created a population of a binary

vector that represents 4 genes (

Table 2). Function

randomGeneration created the initial population,

and crossOver and mutation functions created the

populations of the rest of the generations. A

validation function validated genes. Therefore,

population is biased to create a chromosome with

genes that are on the boundaries of the constraints,

and to create well-dispersed populations. The size of

the population is 30 chromosomes.

Table 2: Genes of the Chromosome.

Gene Name Description

trainVal % of training sample

validVal % of validation sample

testVal % of testing sample

neuL1 number of neurons in hidden layer 1

Table 3: Validation constraints.

Sizes of trainVal, validVal, and testVal should be > 0 and < 98

Total of trainVal, validVal, testVal should be =100

neuL1 should be > 0 and<33

Fitness evaluation was performed as follows;

Gene values of each chromosome were fed into NN

model. The network used MATLAB back

propagation training function – trainlm, with default

training parameters. Function trainlm is considered

as the fastest backpropagation algorithm in the

toolbox, however, it does require more memory than

other algorithms. Function trainlm updates weight

and bias values according to Levenberg-Marquardt

optimisation (MathWorks, 2012).

The information recorded during train, sim, and

regress functions are;

Regression, MSE, and best epoch.

Regression analysis is a statistical tool for the

examination of interaction between variables

(Lindley, 1987). The MATLAB function postreg

was used to calculate the fitness value [R]egression.

The function performs a linear regression between

ImprovedDetectionofProbeRequestAttacks-UsingNeuralNetworksandGeneticAlgorithm

347

the NN output and the target, and computes the

correlation coefficient (R value). Stochastic

Universal Sampling (SUS) was used for selecting

chromosomes for recombination. SUS uses a single

random value to sample all of the solutions by

choosing them at evenly spaced intervals. Therefore,

it offers zero bias and minimum spread (Baker,

1987). A fitness scaling was performed using

MATLAB function fitscalingrank. A pre-determined

% of the total population was selected for crossover

using MATLAB function selectionstochunif. Single

point crossovers were performed. The position of the

crossover was generated randomly. The concepts of

élitism and population overlaps were used in

creating new population, i.e. one elite chromosome,

which is the best performed chromosome from each

generation, was migrated to the next generation.

Selected chromosomes were crossed until 29 more

valid chromosomes were generated to complete the

next generation. Chromosomes to be mutated and

position to be mutated were selected randomly.

Mutated chromosomes were validated using

conditions in

Table 3. The stopping criterion for the

GA is when maximum number of generations is

reached or when there is no improvement.

The GA was set for 100 generations with 30

chromosomes in each generation, and 4 different

types of genes in each chromosome. This

experiment was run on a Toshiba Satellite Pro M70

laptop with an Intel® Pentium® M 740 (1.73GHz)

microprocessor and 1.9 gigabytes of Random Access

Memory, Microsoft Windows XP OS, and a

standard JDK with MATLAB 2008b. Matlabcontrol

Java API was used to interface Java and MATLAB.

4 RESULTS AND DISCUSSION

The GA was run several times with different

parameters. The following presents 3 unique GAs

that shaped the ultimate objective of the research.

The initial GA was executed up to 59 generations

with maxNeurons=25, 1% of single point mutations.

fitnessScale=0.6. To maintain mutation at 1% of

total population, mutation was performed on one

newly formed offspring at every 3rd generation. The

GA was stopped when there was no improvement in

regression value after 42nd generation. Minimum

and maximum MSEs were 0.0035 and 0.0046.

Regression values reported were between 0.9560

and 0.9679. GA converged at 8

generation when

trainVal, validVal, testVal and neuL1 were 21, 33,

39 and 3 respectively. When the results were

analysed, it was found that insufficient

chromosomes were validated to the next generation,

resulting rapid diversity reduction in the population.

Therefore, in the 2nd GA, the maxNeurons were

increased to 32, and fitnessScale rate to 90%. The

GA was executed up to 76 generations. The GA was

stopped when there was no improvement in

regression value after 41st generation. Minimum and

maximum MSEs were 0.0036 and 0.0045.

Regression values reported were between 0.9578

and 0.9691. GA converged at 2nd generation when

trainVal, validVal, testVal and neuL1 were 24, 06,

70 and 27 respectively. When the results were

analysed, it was found that the problem of

insufficient validated chromosomes to the next

generation, still causes rapid diversity reduction in

the population. Further analysis showed that the

strict validation rules restricted achieving diversity.

Although, the research used a high selection and

crossover probability, the validation after crossover

and mutation rejects a major percentage of new

offspring migrating into the next generation.

Selection, crossover and mutation play a major role

in evolution, creating diversity. Therefore, in nature

and in GAs, the key feature for good performance is

to sustain the diversity of the population. Selection

methods also can lead to reduce diversity swiftly.

Therefore, the validation rules of GA were revised to

accept offspring, by scaling the absolute values to

relative values of 100%, so that the total of

trainVal+validVal+testVal will always equal to 100.

The calculations were performed using the Largest

Remainder Method. SUS was not changed as there

was no visible effect between 60% and 80% rates

during previous tests. However, a two-point

mutation was performed. Revision of maxNeurons

may also have improved the diversity and results.

However, current hardware constrains restrict

increasing the neuL1 limit.

The GA3 was executed up to 100 generations.

GA converged at 12th generation. Maximum overall

regression value 0.97682 was achieved when

trainVal, validVal, and testVal and neuL1 were 1,

43, 56 and 6 respectively. Minimum regression

value 0.96101 was achieved when trainVal,

validVal, and testVal and neuL1 were 41, 39, 20 and

17 respectively. Minimum and maximum MSEs

were 0.0084378 and 0.0036468 (Figure 2). The

search space analysis showed a considerably good

diversity in chromosomes generated by the GA.

All GAs generated impressive results with R>

0.95, which is very close to the ideal fitness value of

1. This shows that the training data is

comprehensive. It was achieved due to the large

training sample. Obtaining a large training sample

SECRYPT2012-InternationalConferenceonSecurityandCryptography

348

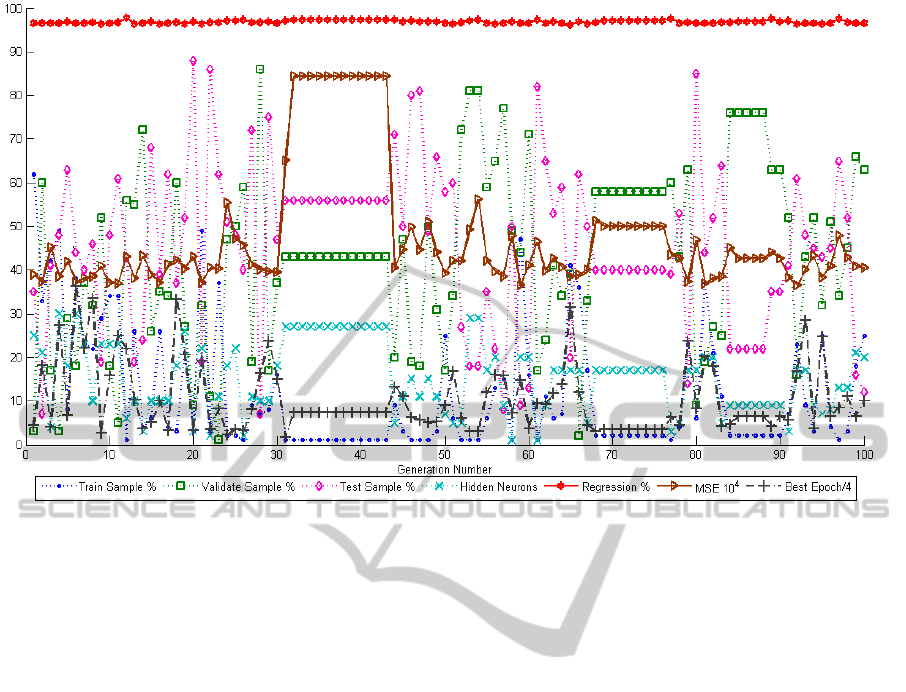
Figure 2: The evolution of the best performed chromosome of each generation (GA3).

and labelling them was possible as normal and

attack data were collected separately. The final

fitness value 0.97682, outperforms or similar to the

GA applications presented in (Gong et al., 2005);

(Haddadi et al., 2010); (Hua and Xiaofeng, 2008);

(Xia et al., 2005), where the results have obtained

using sample traffic databases or synthetic traffic.

This complete research was performed in a real

environment, i.e. capturing of training data (used for

training, validation and testing of NN) and

simulation data were from a real home WLAN.

However, the GA never reached the R value

obtained in (Ratnayake et al., 2011). Population of

trainVal, validVal, and testVal and NeuL1 were

between 1-62, 1-86, 7-88 and 1-30 respectively,

whereas (Ratnayake et al., 2011) used 70, 15, 15 and

20 respectively (Table 1). Hence, although all the

regression results are very close to global optimality

and ideal fitness value of 1, it is reasonable to

suggest that the GA could be further improved.

5 CONCLUSIONS

IEEE 802.11 is the standard for WLAN

communication. Attackers manipulate the request-

response design vulnerability and send a flood of

probe request frames which can cause serious

performance degradation or prevent legitimate users

from accessing network resources.

The research investigates and analyses WLAN

traffic captured on a typical home wireless network,

and uses supervised feedforward neural network

with 4 input neurons, one hidden layer and an output

neuron to determine the results. Empirical results

show that all models perform similarly well.

The research utilised a GA to optimise structure

of the neural network. The paper presents the

process of systematic improvement of the GA and

issues occurred during implementation. The

regression value of the final GA was 0.97682, which

outperforms or similar to current research in the

field of WIDS. However, GA did not reach the R

value 0.98043 obtained in Ratnayake et al. (2011) as

it never simulated with exact combination of NN

structural values. However, the minimum regression

value 0.96101 suggests that this NN model can be

applied to unseen data successfully. The computer

simulation results and optimisation results

demonstrated that this approach helps the NN

designer to find an optimised and reliable NN model

using GAs without searching for every conceivable

combination. Further research will be conducted in

the future to enhance this experiment to optimise the

NN training function.

ImprovedDetectionofProbeRequestAttacks-UsingNeuralNetworksandGeneticAlgorithm

349

REFERENCES

Baker, J. E., (1987). Reducing bias and inefficiency in the

selection algorithm. 2nd International Conference on

Genetic Algorithms on Genetic algorithms and their

application, MIT, Massachusetts.

Bankovic, Z., Stepanovic, D., Bojanic, S., and Nieto-

Taladriz, O., (2007). Improving network security

using genetic algorithm approach. Computers and

Electrical Engineering, 33(5-6), 438-451. doi:

10.1016/j.compeleceng.2007.05.010.

De Jong, K. A., (1993). Genetic algorithms are NOT

function optimizers. FOGA-92, 2nd workshop on

Foundations of Genetic Algorithms, Vail, Colorado.

Gong, R. H., Zulkernine, M., and Abolmaesumi, P.

(2005). A software implementation of a genetic

algorithm based approach to network intrusion

detection. Sixth International Conference on Software

Engineering, Artificial Intelligence, Networking and

Parallel/Distributed Computing, and First ACIS

International Workshop on Self-Assembling Wireless

Networks., 246-253. doi: 10.1109/SNPD-

SAWN.2005.9.

Haddadi, F., Khanchi, S., Shetabi, M., and Derhami, V.,

(2010). Intrusion Detection and Attack Classification

Using Feed-Forward Neural Network. Second

International Conference on Computer and Network

Technology, Bangkok.

Holland, J. H., (1975). Adaptation in natural and artificial

systems : an introductory analysis with applications to

biology, control, and artificial intelligence. Ann

Arbor, Mich.: University of Michigan Press.

Hua, J., and Xiaofeng, Z., (2008). Study on the network

intrusion detection model based on genetic neural

network. International Workshop on Modelling,

Simulation and Optimization, Hong Kong.

Karygiannis, T., and Owens, L., (2002). Wireless network

security. NIST special publication, 800, 48.

Landau, L. G., and Taylor, J. G., (1997). Concepts for

neural networks: A survey: Springer-Verlag New

York, Inc.

Levine, D., (1997). Commentary—Genetic Algorithms: A

Practitioner's View. INFORMS Journal on Computing,

9(3), 256-259.

Li, W., (2004). Using genetic algorithm for network

intrusion detection. United States Department of

Energy Cyber Security Group 2004 Training

Conference, Kansas City, Kansas.

Lindley, D. V., (1987). Regression and correlation

analysis. New Palgrave: A Dictionary of Economics,

4, 120-123. doi: 10.1057/9780230226203.3411.

MathWorks, (2012). Post-Training Analysis (Network

Validation): Multilayer Networks and

Backpropagation Training (Neural Network

Toolbox™) Retrieved 10 May, 2012, from

http://www.mathworks.co.uk/help/toolbox/nnet/ug/bss

3318-1.html.

Moore, A. W., (2001). Cross-validation for detecting and

preventing overfitting Retrieved 10 May, 2012, from

http://www.autonlab.org/tutorials/overfit10.pdf.

Pillai, M. M., Eloff, J. H. P., and Venter, H. S., (2004). An

approach to implement a network intrusion detection

system using genetic algorithms. South African

Institute for Computer Scientists and Information

Technologists on IT research in developing countries,

Republic of South Africa.

Ratnayake, D., Kazemian, H., Yusuf, S., and Abdullah, A.,

(2011). An Intelligent Approach to Detect Probe

Request Attacks in IEEE 802.11 Networks.

Engineering Applications of Neural Networks, Corfu,

Greece.

Reeves, C. R., and Rowe, J. E. (2003). Genetic

algorithms: principles and perspectives: a guide to GA

theory (Vol. 20): Springer.

Wu, S. X., and Banzhaf, W., (2010). Review: The use of

computational intelligence in intrusion detection

systems: A review. Appl. Soft Comput., 10(1), 1-35.

doi: 10.1016/j.asoc.2009.06.019.

Xia, T., Qu, G., Hariri, S., and Yousif, M., (2005). An

efficient network intrusion detection method based on

information theory and genetic algorithm. 24th IEEE

International Performance, Computing, and

Communications Conference, 2005, Phoenix, Arizona.

Yao, X. H., (2010). A network intrusion detection

approach combined with genetic algorithm and back

propagation neural network. International Conference

on E-Health Networking, Digital Ecosystems and

Technologies, Shenzhen.

Zhang, Y., Zheng, J., and Ma, M., (2008). Handbook of

research on wireless security: Information Science

Reference-Imprint of: IGI Publishing.

SECRYPT2012-InternationalConferenceonSecurityandCryptography

350