
Coverage based Test Generation for Duration Systems
Maha Naceur, Lotfi Majdoub and Riadh Robbana
LIP2 Laboratory, Faculty of Sciences of Tunis, Tunis, Tunisia
Abstract. In this paper, we are interested in generating test cases for duration
systems with respect to coverage criteria. Duration systems are an extension of
real-time systems for which delays that separate events depend on the accumu-
lated times spent by the computation at some particular locations of the system.
We present a test generation method for duration systems by considering cover-
age criteria. This method uses the approximation approach and extends a model
using an over approxima- tion, the approximate model, containing the digitiza-
tion timed words of all the real computations of the duration system. Then, we
propose an algorithm that generates a set of test cases presented with a tree by
considering a discrete time and respecting a coverage criterion in order to select
test cases.
1 Introduction
Testing is an important validation activity that aims to check whether an implementa-
tion, referred to as an Implementation Under Test (IUT), conforms to its specification.
The testing process is difficult, expensive and time-consuming. A promising approach
to improve testing consists in automatically generating test cases from formal models
of specification. Using tools to automatically generate test cases may reduce the cost of
the testing process.
In this work, we are interested in testing duration systems. Duration systems are
an extension of real-time systems for which, in addition to constraints on delays sepa-
rating certain events that must be satisfied, constraints on accumulated times spent by
computation must also be satisfied. Timed automata constitute a powerful formalism
widely adopted for modeling real-time systems [2]. Duration Variables Timed Graphs
with Inputs Outputs (DVTG- IOs) are an extension of timed automata [3], which are
used as a formalism to describe duration systems. DVTG- IOs are supplied with a finite
set of continuous real variables that can be stopped in some locations and resumed in
other locations. These variables are called duration variables.
For testing real-time systems, most works borrow several techniques from the real-
time verification field due to similarities that exist between model-based testing and
formal verification (e.g., symbolic techniques, region graph and its variations, model
checking techniques, etc.). Those techniques are used particularly to reduce the infinite
state space to a finite or countable state space. Then they adapt the existing untimed
test case generation algorithm. We cite as examples [6][8][9]. It is well known that the
verification of real-time systems is possible due to the decidability of the reachability
Naceur M., Majdoub L. and Robbana R..
Coverage based Test Generation for Duration Systems.
DOI: 10.5220/0004089000030014
In Proceedings of the 10th International Workshop on Modelling, Simulation, Verification and Validation of Enterprise Information Systems and 1st
International Workshop on Web Intelligence (MSVVEIS-2012), pages 3-14
ISBN: 978-989-8565-14-3
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

problem for real-time systems [1]. However, it has been shown that the reachability
problem is undecidable for timed graphs extended with one duration variable [5] and,
consequently, it is not possible to use classical verification techniques to generate test
cases for DVTG-IO.
We give in this paper a method for generating test cases with respect to coverage
criteria for duration systems. In practice, Complete test cases cannot be performed in a
finite time. This implies that a strategy of test selection should be done to choose the
adequate test cases to be applied in the implementation under test. Coverage criteria are
a measure allowing to select test cases according to some criteria. Different coverage
criteria have been proposed such as statement coverage, branch coverage and so on [17].
Here, we propose a technique to select test cases according to state coverage criterion
and transition criterion.
Formally, we describe the specification as well as the implementation under test
with DVTG-IO. In order to reduce the infinite state space to a finite state space, we use
the approximationmethod that extends a given DVTG-IO specification to another called
the approximate model that contains the initial test cases as well as their digitizations.
An algorithm for generating a set of test cases, satisfying a coverage criterion, is given.
We present this set of test cases by a tree.
This paper is organized as follows: In the next section, we present the duration
variables timed graphs with inputs outputs. In section 3, we present the approximation
method. Section 4 shows our testing method for generating tests with respect to cover-
age criteria. Section 5 gives conformance relation to show that the generated test cases
are sound. Concluding remarks are presented in section 6.
2 Duration Variables Timed Graphs with Inputs Outputs
A DVTG-IO is described by a finite set of locations and a transition relation between
these locations. In addition, the system has a finite set of duration variables that are
constant slope continuous variables, each of them changing continuously with a rate
in {0,1} at each location of the system. Transitions between locations are conditioned
by arithmetical constraints on the values of the duration variables. When a transition is
taken, a subset of duration variables should be reset and an action should be executed.
This action can be either an input action, an output action or an unobservable action
[16].
2.1 Formal Definition
We consider X a finite set of duration variables. A guard on X is a boolean combination
of constraints of the form x ≺ c where x ∈ X, c ∈ N, ≺∈ {<, ≤, >, ≥ }. Let
Γ (X) be the set of guards on X. A DVTG-IO describing duration systems is a tuple
S = (Q, q
0
, E, X, Act, γ, α, δ, ∂) where :
• Q is a finite set of locations,
• q
0
is the initial location,
• E ⊆ Q × Q is a finite set of transitions between locations,
• Act = Act
In
∪ Act
Out
∪ {τ} is a finite set of input actions (denoted by ?a), output
4

actions (denoted by !a) and unobservable action ξ,
• γ : E −→ Γ (X) associates to each transition a guard which should be satisfied by
the duration variables whenever the transition is taken,
• α : E −→ 2
X
gives for each transition the set of duration variables that should be
reset when the transition is taken,
• δ : E −→ Act gives for each transition the action that should be executed when the
transition is taken,
• ∂ : Q × X −→ {0, 1} associates with each location q and each duration variable x
the rate at which x changes continuously in q.
Example. To illustrate DVTG-IO, we show on Fig.1 the specification of a vending
machine. This machine delivers a beverage after receiving a coin from the user. It is
composed of locations {q
0
, q
1
, q
2
, q
3
, q
4
, q
5
} where q
0
is the initial location, transitions
between locations and is supplied with a set of input actions {?choose, ?coin}, output
actions {!price, !accept, !delive r, !returncoi n, !re turn, !timeout} and three duration
variables x, y, z. Duration variables x and y are clocks used to make constraints on the
time execution of the vending machine, z is a duration variable, it is stopped in q
0
, q
2
and it is used to make constraints on the time spent by the system. The behavior of this
machine can be describes as follows:
- In the initial node q
0
, the system waits for the user to choose a beverage. The user can
decide his choice during a time unit.
- In the node q
1
, the machine tells the user the price of the drink chosen and pass to the
node q
2
.
- In the node q
3
, the machine checks the coins; if they are accepted, it enters the node
q
4
and provides the drink, otherwise it returns coins and passes to q
0
.
2.2 State Graph
The semantic of DVTG-IO is defined in terms of a state graph over states of the form
s = (q, ν) where q ∈ Q and ν : X −→ R
+
is a valuation function that assigns a real
value to each duration variable. Let St
S
be the set of states of S. We notice that St
S
is
an infinite set due to the value of duration variables taken on R
+
. A state (q, ν) is called
integer state if ν : X −→ N. We denote by N (St
S
) the set of integer states of S.
Given a valuation ν and a guard g, we denote by ν |= g the fact that valuation of g
under the valuation v is true.
We define two families of transition between states : discrete transition (q, ν)
a
(q
′
, ν
′
) with (q, q
′
) ∈ E, δ(q, q
′
) = a, ν |= γ(q, q
′
) is true and ν
′
(x) = ν(x)
∀x ∈ X\α(q, q
′
) , ν
′
(x) = 0∀x ∈ α(q, q
′
), that corresponds to moves between
locations using transition in E; timed transition (q , ν)
t
(q, ν
′
) such that t ∈ R
+
and ν
′
(x) = ν(x) + ∂(q, x) ∗ t ∀x ∈ X, that corresponds to transitions due to time
progress at some location q. The state graph associated with S is (St
S
, ֒→) where ֒→
denotes the union of all discrete and timed transitions.
2.3 Computation Sequences and Timed Words
A Computation sequence of a DVTG-IO is defined as a finite sequence of configura-
tions. A configuration is a pair (s, τ) where s is a state and τ is a time value. Let C
S
be
5
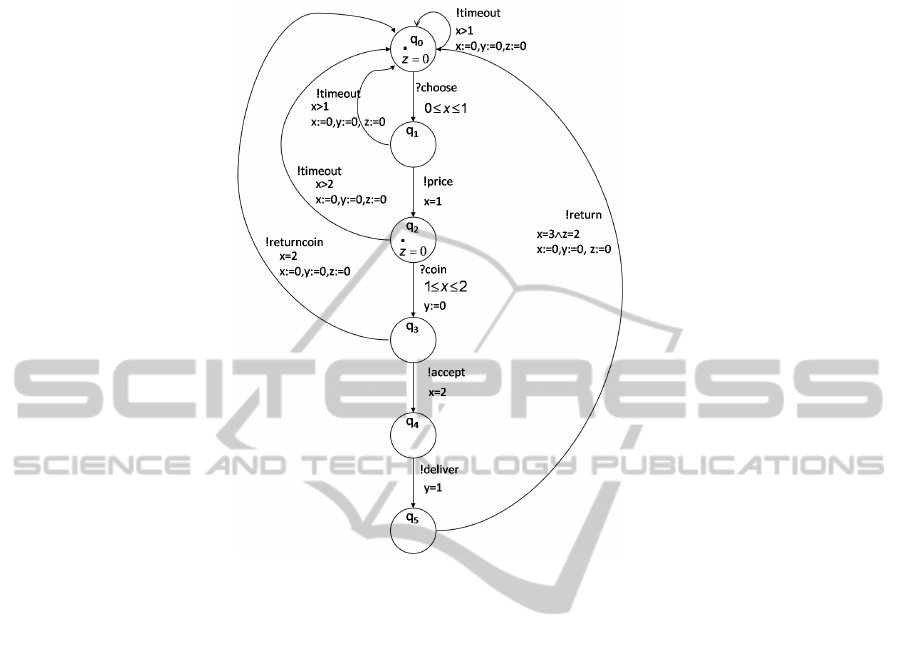
Fig.1. DVTG-IO of a vending machine.
the set of configurations of S. Intuitively, a computation sequence is a finite path in the
state graph of an extension of S by an observation clock that records the global elapsed
time since the beginning of the computation.
Formally, if we extend each transition relation from states to configurations, then
a computation sequence of S is σ = (s
0
, 0) (s
1
, τ
1
) ... (s
n
, τ
n
), where
s
i
= (q
i
, ν
i
) and τ
i−1
≤ τ
i
for i = 1..n. Let C
S
(S) be the set of computation sequences
of S. A timed word is a finite sequence of timed actions. A timed action is a pair aτ
where a ∈ Act and τ ∈ R
+
, meaning that action a takes place when the observation
clock is equal to τ . A timed action aτ is called integer timed action if τ ∈ N. A timed
word is a sequence ω = a
1
τ
1
a
2
τ
2
...a
n
τ
n
where a
i
is an action and τ
i
is a value of the
observation clock. We notice thatτ
i
≤ τ
i+1
. Let L(S) be the set of timed words of S.
A sequence ω = a
1
τ
1
a
2
τ
2
...a
n
τ
n
is considered a timed word of L(S) if and only if
there exists a computation sequence σ = (s
0
, τ
0
) (s
1
, τ
1
) ... (s
n
, τ
n
) ∈
CS(S) such that a
i
= δ(q
i−1
, q
i
) for i = 1, .., n and s
i
= (q
i
, ν
i
). For simplicity, we
may write (s
0
, τ
0
)
ω
(s
n
, τ
n
).
Let ω = a
1
τ
1
a
2
τ
2
...a
n
τ
n
be a timed word and a ∈ Act, τ ∈ R such that τ
n
≤
τ then we denote by ω.aτ the timed word obtained by adding a τ to ω and we have
ω.aτ = a
1
τ
1
a
2
τ
2
...a
n
τ
n
aτ.
6

3 Approximation
The approximation method is used in the verification of duration systems [14]. It allows
to reduce the infinite set of states to a finite set. We adapt this method to test duration
systems.
3.1 Digitization
We present the notion of digitization [7], which is suitable for the systems in which we
are interested. Let τ ∈ R
+
. For every ǫ ∈ [0, 1[, called digitization quantum, we define
the digitization of [τ]
ǫ
= ⌊τ ⌋ if τ ≤ (⌊τ⌋ + ǫ) else [τ]
ǫ
= ⌈τ ⌉.
Given ǫ ∈ [0, 1[, , the digitization of a timed word ω = a
1
τ
1
a
2
τ
2
...a
n
τ
n
is [ω]
ǫ
=
a
1
[τ
1
]
ǫ
a
2
[τ
2
]
ǫ
...a
n
[τ
n
]
ǫ
.
Therefore, it is not difficult to see that: [ω.at]
ǫ
= [ω]
ǫ
.a[t]
ǫ
Moreover, it is easy to
relate digitizations of a computation sequence and its timed word. If σ is a computation
sequence and ω is its corresponding timed word then for ǫ ∈ [0, 1[, [ω]
ǫ
is the corre-
sponding timed word of [σ]
ǫ
. We denote by Digit(L(S)) the set of all the digitizations
of all the real timed word of S. We notice that Digit(L(S)) is countable. The digiti-
zation is used to reduce the infinite set of states to a finite set of states. A question that
one may ask is whether Digi t(L(S)) ⊆ L(S) or not.
3.2 Approximate Model
As we have seen in the previous example, some timed words of a DVTG-IO do not have
any digitizations in S. The idea given in [14] consists of over approximating the model
S by an approximate model S
′
such that D igit(L(S)) ⊆ L(S
′
).
Definition 1: The function β : X × E −→ N calculates for each variable x ∈ X and
each transition e = (q, q
′
) the maximum of restarts of x from the last reset of x until
the location q in each way.
A restart of a variable x is the change of its rate from 0 to 1. After a reset of a
variable x, if the rate of a variable x in the current location is 1, then the access to this
location is considered as a restart of x. That is why, for the clocks, the function β is
equal to 1 for each transition.
Definition 2: The approximate model S
′
= App(S) is obtained from S by transform-
ing each guard of a transition e of the form u ≺ y ≺ w by the guard:
If u − β(y, e) ≥ −1 then u − β(y, e) + 1 ≤ y ≤ w + β(y, e) − 1 else 0 ≤ y ≤
w + β(y, e) − 1 where u, w ∈ N, x ∈ X, et ≺∈ {<, ≤}.
Proposition 1: ∀ ω ∈ L(S) we have [ω]
ǫ
∈ L(S
′
) for each ǫ ∈ [0, 1[.
This proposition demonstrates that for every timed word of the specification model,
its digitizations belong to the approximate model.
Example. If we apply the approximation method on the DVTG-IO of the Fig.1, we
obtain the approximate model on the Fig.2. It involves replacing the guard x=3 ∧ z=2
associated with the transition (q
5
, q
0
) with the guard x=3 ∧ 1 ≤ z ≤ 3 because we have
β (z, (q
5
, q
0
) ) = 2
7
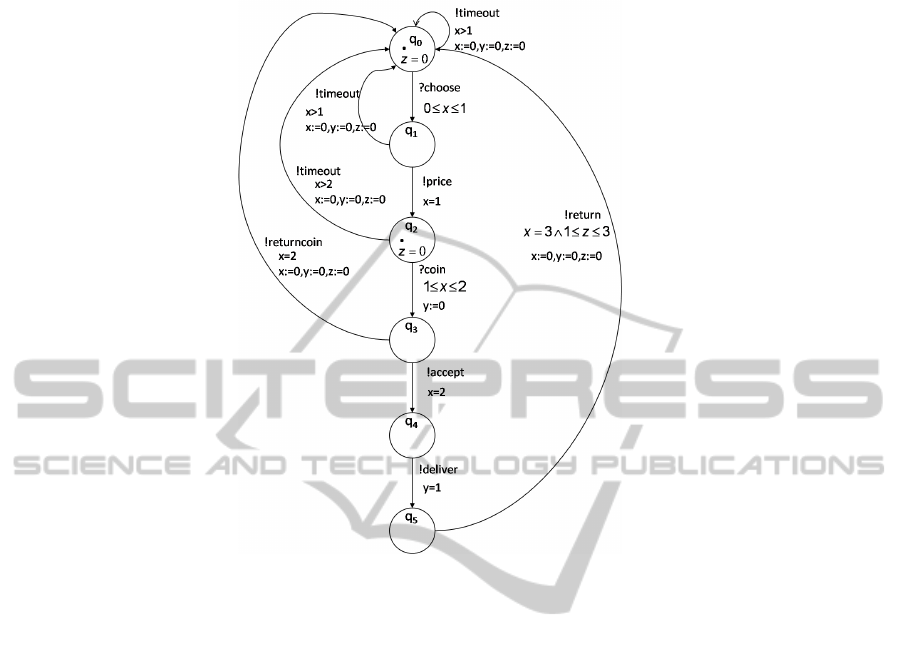
Fig.2. The approximate model of a vending machine.
3.3 Test Generation with the Approximate Model
First, let us introduce the notion of an observation which is a sequence of controllable
(inputs) and observable (outputs) actions that are either executed or produced by the
IUT followed by its occurrence time. Formally, we describe an observation by a timed
word ω = a
1
τ
1
a
2
τ
2
...a
n
τ
n
where a
i
∈ Act and τ
i
∈ R
+
for i = 1..n.
Our result is based on a reduction of the infinite state graph associated with S
′
=
App(S) to the countable state graph (N(St
S
′
),
1
∪
a
), where the space of states is
the set of integer states. Transitions between states are either discrete transition(q, ν)
a
(q
′
, ν
′
) labeled with action in Act, or timed transition (q, ν)
1
(q, ν
′
) labeled with
a constant delay of time equal to 1. Notice that ν and ν
′
∈ [X → N]. Clearly, the
digitizations of all timed words Digit(L(S)) are included in (N(St
S
′
),
1
∪
a
).
We define a number of operators that we use in the algorithm of generating test tree.
Let C be a configuration of (N(St
S
′
),
1
∪
a
) and aτ is timed action.
Out(C)(resp. In(C)) is the set of all timed output actions (resp. the set of all timed
input actions) that can occur when the system is at configuration of C. Furthemore, C
after aτ is the set of all configurations that can be reached from C after the execution
of the timed word aτ. Notice that Ou t(C), In(C) and C after aτ are finite sets. They
are calculated in (N(St
S
′
),
1
∪
a
).
8
3.4 The Test Tree
We use the countable state graph (N(St
S
′
),
1
∪
a
) to generate a finite set of test
cases. This set of test cases is represented by a tree called Test Tree. The test tree is
composed by nodes that are sets of integer configurations and transitions between those
nodes. A node in the test tree is a finite set of integer configurations (s, τ ) such that
s ∈ (N(St
S
′
)), τ ∈ N and represents the possible current integer configurations of the
IUT. The root is the initial configuration of (N(St
S
′
),
1
∪
a
) that is (s
0
, τ
0
).
The transition between one node and its successor is labelled with a timed action
aτ such that a ∈ Act and τ ∈ N. A path from the root to one leaf of the tree represents
a digitization of a timed word.
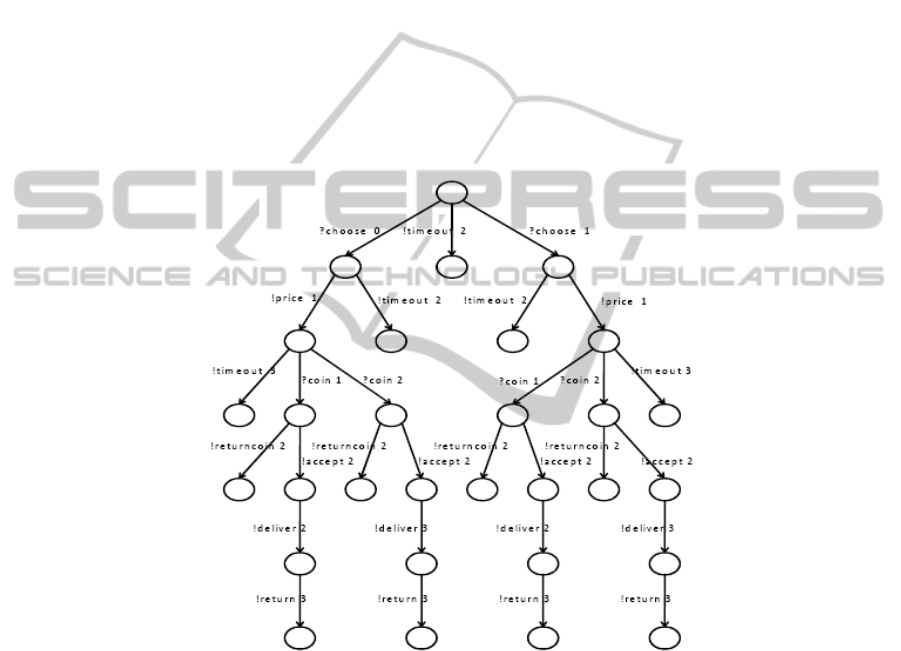
Example. An example of test tree is given in fig.3. It is constructed from the approxi-
mate model of fig.2. Each path of the test tree from the root to a leaf corresponds to an
integer computation sequences of the approximate model. Notice that is a complete test
tree, it contains all possible integer test cases belonging to the approximate model.
Fig.3. The test tree.
4 Generating Tests with Respect to Coverage Criteria
Here, we introduce our approach to generating test cases for duration systems that is
based on the approximation method and with respect to coverage criteria.
4.1 Coverage Criteria
In practice, generating a complete test case cannot be executed in a finite time. The aim
9

of the tester is to generate a set of test cases that cover the state graph of the specification
model.
This implies that the tester should apply a strategy of test selection that allows to
choose the adequate test cases to be applied on the implementation under test. Coverage
criteria are a measure used to select test cases according to some criteria. A large suite
of coverage criteria has been proposed in the literature. Different coverage criteria have
been proposed such as location coverage, edge coverage and so on [16].
We present here two types of coverage criteria that we use to select test cases from
the state graph of a DVTG-IO model:
• State coverage : A set of test cases satisfies the state coverage criterion if, when exe-
cuted on the model, they visit every state of the state graph model. In other words, every
state is covered by some test case. Notice that the set of states is infinite. A set of test
cases covering states also covers transitions. However, it may not cover all transitions
of the model.
•Transition coverage : test cases satisfy the transition coverage criterion if, when exe-
cuted on the model, they traverse every transition of the specification model. We can
distinguish here between discrete transition and timed transition.
4.2 Algorithm of Coverage Generating Test Tree
We adapt the testgeneration algorithm of [13] in order to select test cases. The following
algorithm considers only the test cases that satisfy the coverage criteria. These test cases
are represented by a test tree. The coverage criterion considered in this algorithm is the
state coverage of the state graph of the approximate model.
Algorithm 1: Coverage Generating Test Tree.
1 Input : N(G
S
′
) = (N (St
S
′
),
1
∪
a
)
2 Output : Test Tree T
3 T = T
′
= {(s
0
,0)} the one-node tree
4 while T
′
6= T
5 T := T
′
6 for each leaf C of T distinct from pass
7 Out(C) ; In(C)
8 if Out(C) ∪ In(C) = ∅ then
9 C = pass
10 else
11 for each aτ ∈ Out(C) ∪ In(C)
12 C
′
= C af ter aτ
13 if not exist(C
′
, T
′
)
14 append edge C
aτ
C
′
to T
15 End while
16 End
The coverage generating test tree algorithm operates as follows : initially the test
tree contains one node that is the initial configuration of S
′
: (s
0
, 0). For every leaf C
of the tree distinct from pass, the algorithm calculates the set of integer timed actions
(In(C) and Out(C)) that can be taken when the system is in C. For each timed action
10

aτ belonging to Out(C)
S
In(C) the algorithm claculates C
′
= C after aτ, the set
of configurations obtained when aτ is executed.
The edge C
aτ
C
′
is appended to the test tree if C
′
does not belong to the test tree.
The algorithm can stop branching a path of the tree by appending the node pass in the
leaf that has not any timed action (In(C)
S
Out(C)=∅).
Example. To illustrate the above algorithm, we consider the approximate model of the
vending machine. A possible test tree, respecting the state coverage criterion, is given
in fig.4.
However, it is not difficult to replace this criterion with transition coverage. An
algorithm was also implemented to generate test cases respecting the coverage of tran-
sitions. In this algorithm, the transition C
aτ
C
′
is added to the tree test if C
′
does not
already exist.
Fig.4. DVTG-IO of a vending machine.
Now, we demonstrate that a path in the test tree obtained by the Coverage Gener-
ating Test Tree Algorithm corresponds to a timed word that is a digitization of the one
timed word of the specification model describing a duration system.
Proposition 2: Let ω ∈ L(S) be a timed word and [ω]
ǫ
∈ L(S
′
) its digitization for
ǫ ∈ [0, 1[, if ∃ a ∈ Act and ∃τ
′
∈ N such that [ω]
ǫ
.aτ
′
∈ L(S
′
) then ∀τ ∈]τ
′
− 1 +
ǫ, τ
′
+ ǫ ] we have ω.aτ ∈ L(S).
The test generation from the approximate specification model can give to the tester
the action and the integer time value of its execution on the IUT in discrete time. The
above proposition shows that if the tester executes the action (input or output) within a
11

real-time interval,defined by the proposition 2, then the conformance of the observation
recorded on the IUT is preserved according to the approximate model.
Proposition 3: Let ω = a
1
τ
1
a
2
τ
2
...a
n
τ
n
be a timed word that corresponds to a path
from the root to a leaf in T
S
, then ∃ ω
′
∈ L(S) such that [ω
′
]
ǫ
= ω
Proof: We proceed by a recursive proof on the size of ω. Let ω
i
= a
1
τ
1
a
2
τ
2
...a
i
τ
i
with
i ≤ n be the timed word obtained in the level i of the test tree, we have ω
n
= ω. For
i = 0, ω
0
= ∅ the proposition is true because (ω
′
0
= ∅) ω
′
0
∈ L(S) and we have
[ω
′
0
]
ǫ
= ω
0
.
For i < n, we suppose that the proposition is true for i and we try to demonstrate
for i + 1, ∃ ω
′
i
∈ L(S) such that [ω
′
i
]
ǫ
= ω
i
. Given aτ ∈ Out(S
′
after ω
i
) ∪
In(S
′
after ω
i
), we have ω
i
.aτ ∈ L(S
′
). From the proposition 2, ∀τ
′
∈] τ − 1 + ǫ,
τ + ǫ ] we have ω
′
i
.aτ
′
∈ L(S).
So [ω
′
i
.aτ
′
]
ǫ
= ω
i
.aτ .
A path in the test tree is a discrete timed word obtained from the countable state
graph (N(St
S
′
),
1
∪
a
) associated to the approximate model S
′
= App(S). In
proposition 3, we demonstrate that a path in the test tree corresponds to a digitization
of a timed word belonging to the initial model S.
By considering this result and the result obtained in the proposition 2, we can use
the test tree to generate a discrete test case, then we can experiment it by considering
continuous time. For generating an input timed action that should be executed on the
IUT, the tester chooses one integer timed action aτ from the test tree. By proposition 2,
the action a can be applied within the real-time interval ]τ − 1 + ǫ, τ + ǫ].
5 Conformance Relation
5.1 Definition of the Dioco Relation
In this section we present a conformance relation to show that the generated test cases
from the approximate model are sound, including those that meet the coverage criteria.
We recall the definition of the duration input output conformance relation (dioco
for short) first introduced in [12] and which is in turn inspired from the untimed con-
formance relation (ioco) of [16].
Let S be the DVTG-IO representing the specification of a duration system and Imp
be a DVTG-IO representing the implementation under test. The duration input output
conformance relation, denoted dioco, is defined as :
Imp dioco S ⇐⇒
def
∀ ω ∈ L(S) Out(Imp after ω)⊆ Out(S after ω).
The dioco relation states that an implementation Imp conforms to its specification
S if and only if for any observation ω of S, the set of observable timed output actions
obtained after the application of ω on Imp must be a subset of the set of possible timed
output actions obtained after the application of ω on S.
5.2 Soundness Coverage Test Cases
Soundness test cases mean that if an implementation conforms to its specification, it
will pass all test cases (timed words) belonging to the set of test cases. In other words,
12

if the implementation fails at least one test case (timed word) then the implementation
does not conform to its specification.
It is well known that soundness property is achievable for practical testing. It is
shown in [3] that it is theoretically possible to produce a complete test case (i.e. sound-
ness and exhaustiveness test cases) but in practice it is not possible to execute an infinite
number of tests in a limited period of time. We prove that test cases satisfying coverage
criteria and generated from the test tree are sounded by considering the conformance
relation dioco.
First, let us define the digitization of the operator Out, given a digitization quantum
ε ∈ [ 0, 1[ and for C ⊆ C
s
is a set of configurations.
[Out(C)]
ε
= {oτ
′
, o ∈ Act
Out
, τ
′
∈ N|∃τ ∈ R
+
, oτ ∈ Ou t(C)and[τ]
ε
= τ
′
}.
Proposition 4: ∀ ω ∈ L(S), if Out(Imp after ω)⊆ Out(S after ω) then for ε ∈ [ 0, 1[,
[Out(Imp after ω)]
ε
⊆ [Out(S after ω) ]
ε
.
Proof: Let oτ
′
∈ [Out(Imp after ω)]
ε
, We remember the definition of the digitization of
the operator Out ; ∃ τ ∈ R
+
, oτ ∈ Out(Imp after ω) and [oτ ]
ε
=oτ
′
. From the hypothesis
of this proposition we have that oτ ∈ Out(S after ω). The definition of the digitization
of the operator Out ensures that [oτ]
ε
∈ [Out(Imp after ω)]
ε
. So oτ
′
∈ Out(S after ω).
Then we conclude that [Out(Imp after ω)]
ε
⊆ [Out(S after ω) ]
ε
.
We deduce from this result and propsition 3 that Imp dioco S ⇐⇒
def
∀ ω ∈ T ,∀ ε
∈ [ 0, 1[ [Out (Imp after ω)]
ε
⊆ [Out(S after ω)]
ε
.
6 Conclusions
We have introduced a method for generating test cases with respect to coverage criteria
for duration systems. First, we used the DVTG-IO as a formalism to model specifica-
tion. Second, we presented the approximation method. This method extends a given
DVTG-IO to another called approximate model that contains the initial test cases as
well as their digitizations.
Then, we proposed an algorithm that generates a set of test cases presented in a
tree by considering a predefined coverage criteria. The coverage criterion, considered
in this paper, is the state coverage. We demonstrated that test cases generated from the
approximate model correspond to the digitization of timed words of the specification
model. At the end, we showed that those test cases are sound by considering the dioco
conformance relation.
In the future work, we plan to implement this algorithm with different coverage
criteria and to apply this approach to other systems such as real-time systems and hybrid
systems.
References
1. Alur R., Courcoubetis C., and Dill D., Model-Checking for Real-Time Systems, 5th Symp.
on logic in Computer Science, 1990.
2. Alur R.and Dill D., A Theory of Timed Automata, Theoretical Computer Science, 126 :
183-235, 1994.
13

3. Bouajjani A., Echahed R., Robbana R., Verifying Invariance Properties of Timed Systems
with Duration Variables, Formal Techniques in Real-Time and Fault Tolerant Systems, 1994.
4. Cassez F, Larsen K.G, The Impressive Power of Stopwatches, Proc. Conference on Concur-
rency Theory CONCUR’00, Penssylvania, USA, 2000
5. Cerans K., Decidability of Bisimulation Equivalence for Parallel timer Processes, In Proc.
Computer Aided Verification (CAV’92), Springer-Verlag, 1992, LNCS 663.
6. En-Nouaary A., Dssouli R., Khender F., and Elqortobi A., Timed Test cases generation based
on state characterisation technique, In RTSS’98. IEEE, 1998.
7. Henzinger T., Manna Z., and Pnuelli A., What good are digital clocks?, In ICALP’92, LNCS
623, 1992.
8. Hessel A., Pettersson P., A Test Case Generation Algorithm for Real-Time Systems, In Proc.
4th international Conference on Quality software, pp. 268-273, 2004.
9. Krichen M, Tripakis S., Black-Box Conformance Testing for Real-Time Systems, SPIN’04
Workshop on Model Checking Software, 2004.
10. Majdoub L. and Robbana R., Testing Duration Systems using an Approximation Method,
Depcos-RELCOMEX, pp.119-126, Szklarska Poreba, Poland, June 2007.
11. Majdoub L. and Robbana R., Testing Duration systems, Journal Européen des Systèmes
Automatisés, vol 42 n
◦
9/2008, pp. 1111-1134, November 2008.
12. Majdoub L. and Robbana R., Test cases generation for nondeterministice duration systems,
7th MSVVEIS, pp.14-23, Milan, Italy, May 2009.
13. Robbana R, Verification of Duration Systems using an Approximation Approach, Journal
Computer Science and Technology, Vol 18, N
◦
2, pp. 153-162, March 2003.
14. Springintveld J., Vaandrager F., and D’Argenio P., Testing Timed Automata, Theoretical
Computer Science, 254, 2001.
15. Tretmans J, Testing Concurrent Systems : A Formal Approach, CONCUR’99 , 10th Int,
conference on Concurrency Theory, pages 46-65, 1999.
16. Zhu H, Hall P, May J, Software unit test coverage and adequacy, ACM Computing Surveys,
29(4), 1997.
14
