
A Grouping Model for Prompt Agent based Damage
Assessment
Naveen Ramanathan
1
, Brajendra Panda
1
and Yi Hu
2
1
Computer Science and Computer Engineering Department, University of Arkansas,
Fayetteville, AR 72701, U.S.A.
2
Computer Science Department, Northern Kentucky University,
Highland Heights, KY 41099, U.S.A.
Abstract. Prompt recovery of data after cyber attacks depends on an efficient
damage assessment mechanism. This paper presents a grouping model for the
agent-based damage assessment method to facilitate quick post information
warfare damage assessment. The grouping method proposed is based on the
longest-dependency-path-first approach and can significantly reduce the
damage assessment latency of the agent based damage assessment process. We
also present an improved damage assessment algorithm that uses this grouping
model to determine the extent of damage to other data items.
1 Introduction
In spite of all intrusion detection mechanisms in existence today, none of them
guarantee that a breach of security will be detected immediately. Hence, there could
potentially be a time lag between the notification of an intrusion and the actual event
of the intrusion itself. Since information systems often compute new information
based on already existing data, as time passes by, legitimate transactions might read
corrupted data values. Through them the damage may spread to the rest of the
database. This can cause a cascading effect and make the recovery process very
difficult. Thus it is of utmost importance to quickly and efficiently assess the extent of
damage done to the database, as well as accurately recover the corrupt data. A graph
based damage assessment model has been proposed in [1]. An agent based damage
assessment model has been proposed in [2]. Once the damage assessment has been
made and the damaged data items identified, the next step is to recover these data
items. Traditional recovery approaches are discussed in [3, 4, 5, 6].
Traditionally, damage assessment techniques are broadly classified under two
categories, namely the transaction dependency approach and the data dependency
approach. In the transaction dependency approach [7, 8] malicious transactions are
identified and marked as damaged and the transactions that read and update values
from these malicious transactions are also marked as damaged. In order to undo the
changes made to the database, the effects of these malicious transactions have to be
removed and each of the affected transactions must be re-executed. The data
dependency approach [1, 9] focuses on just the operations on affected data items
Ramanathan N., Panda B. and Hu Y..
A Grouping Model for Prompt Agent based Damage Assessment.
DOI: 10.5220/0004101301090116
In Proceedings of the 9th International Workshop on Security in Information Systems (WOSIS-2012), pages 109-116
ISBN: 978-989-8565-15-0
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

within a transaction. Thus only those operations need to be undone and redone in
order to restore the database back to the original state. Our research utilizes the data
dependency approach described. An agent-based damage assessment model was
proposed in [2] where individual agents are assigned a group of data items and each
agent performs damage assessment and recovery in parallel. Although this method
could prove to be efficient to perform damage assessment in systems that process
large volumes of data, the research does not address the non-trivial task of
determining a systematic approach to group data items amongst agents. It is of utmost
importance to group related data items together in order for the agent based damage
assessment to work.
2 The Model
Our research focuses on the issue of grouping described in the agent based damage
assessment model proposed in [2]. We utilize the concept of the graph-based
approach described in [1] in order to perform grouping. In the agent-based damage
assessment model, each agent is responsible for a group of data items. The agents then
perform damage assessment and recovery on their group of data items in parallel.
Hence the damage assessment and recovery can be done speedily. However, as
mentioned above, for this model to be effective, it is vital that an efficient approach to
group data items amongst agents be developed. We propose one such grouping
mechanism that could significantly improve the efficiency of agent based damage
assessment. The grouping mechanism utilizes a longest-dependency-path-first
approach which is discussed in the following section. The greatest advantage with this
scheme is that the groups can be pre-computed. When the intrusion detection system
notifies the agents of the initial set of damaged data items, we have agents ready with
their set of data items which are grouped logically based on dependencies. This would
enable the agents to run the damage assessment phase in parallel and greatly reduce
latency of the damage assessment process. We have also proposed an improved agent
based damage assessment mechanism that efficiently utilizes the result of the
grouping process in order to perform damage assessment.
2.1 Grouping Algorithm
The grouping algorithm is responsible for assigning nodes to various groups based on
their dependencies in the graph. The algorithm takes as input the constructed graph
and assigns all the nodes to groups, which in turn are used for damage assessment.
Before introducing the algorithm, we explain the term “distance/index.” The
distance/index of a node is defined as the number of hops that must be taken to reach
that particular node from a given root node(s).
For instance, in Figure 1, the distance/index of node ‘2’ is 1 (from root node ‘1’)
and the distance/index of node ‘7’ is 2 (from root node ‘5’). It is to be noted that a
node can have only one distance/index although it may be reachable from two or more
root nodes. In Figure 1, node ‘3’, ‘4’ and ‘9’ for example can be reached from both
root nodes ‘1’ and ‘5’. Thus node ‘3’ can potentially have two indexes 2 (from root
110

node 1) and 3 (from root node 5). In such a situation, the node is assigned the higher
of the two distance/index values. In this case, node ‘3’ gets an index of 3. The reason
for choosing the higher distance/index value is explained in the following algorithm.
Fig. 1. Basic structure of a graph.
The steps involved in the grouping algorithm are presented below.
Grouping Algorithm
1. Read in nodes and dependencies from the input text file.
2. Construct graph based on dependencies denoted in the file.
3. For all root nodes
3.1 Compute distance (index) to every reachable leaf node from root node.
3.2 Assign incremental index to each node along the way.
4. Sort leaf nodes by descending order of distance from root node.
5. Start from farthest leaf node.
5.1 Add leaf node to new group G
i
(Where i = 1, 2, 3 ….. n).
5.2 Mark leaf node as “added to group”.
5.3 Check if its immediate parent node(s) is “added to group”.
5.4 If ‘yes’, skip parent node and move on to its ancestor. Repeat step 5.3.
5.5 If ‘no’, add parent node to same group and mark parent node as “added to group”.
5.6 Repeat steps 5.3 to 5.5 till root node is reached.
6. Repeat step 5 till all leaf nodes is covered.
7. Check if all nodes are added to groups.
If ‘yes’, skip to step 8.
If ‘no’, repeat step 5 for each node not added to group (Replacing leaf node with current
node).
8. Check if group of size 1 is present.
8.1 Check if node in group is a leaf node.
If ‘yes’, add leaf node to same group as its parent node.
If ‘no’, add node to the same group as its immediate parent or child node.
9. End
Step 1 of the algorithm reads in values of nodes from a text file. The file contains
nodes in a multi line format (P*, C
1
, C
2
…. C
n
), where P denotes a parent node and
C
1
, C
2
…. C
n
denote its respective child nodes. A parent node denoted by a ‘*’
represents a root node. As stated in the earlier section, a graph may contain more than
one root node.
Step 2 of the algorithm links these parent-child relationships and constructs a
complete graph.
In step 3, the root node from the graph is taken as a reference and the distance to
each reachable leaf node from that particular root node is estimated. This step is
111

repeated for all root nodes in the graph. Also, each internal node along the path to a
particular leaf node is assigned an index (which is the distance from the root node).
It is to be noted that an internal node may appear more than once in different paths
to individual leaf nodes, thus having multiple indexes. In such a situation, the internal
node is assigned an index which is the highest of all its computed indexes. This
ensures that the node belongs to the longest possible path to that particular leaf node.
Once all possible distances from all root nodes in the graph to all its respective
reachable leaf nodes are computed, step 4 of the algorithm sorts these distances in
descending order. This is done in order to group nodes based on the longest-
dependency- path-first approach.
Step 5 forms the most important part of the algorithm. Starting from the farthest
reachable leaf node computed in the above step, the leaf node is added to a new group
and marked as ‘added to group’. Then the immediate parent of the leaf node is added
to the same group contingent upon whether or not it is marked as ‘added to group’.
This is done at each step to ensure that a node does not appear in more than one
group. If the parent node is not marked, it is added to the same group, otherwise it is
skipped and the algorithm proceeds to its parent node and so on till the respective root
node is reached.
The algorithm then proceeds to the next farthest leaf node and follows the same
process till all leaf nodes are covered.
Finally, when all nodes are grouped, step 7 checks for groups that contain a single
node in them. In such a case, if the node contained in the group were a leaf node, it is
added to the same group as its immediate parent. If the node were any other, it is
added to the same group as its immediate parent node (in case of an internal node) or
its immediate child node (in case of a root node).
2.2 Damage Assessment Algorithm
The damage assessment process determines the extent of propagation of damage
amongst data items by building a damaged list. An initial list of damaged data items is
produced by the intrusion detection system. The agents are then notified about these
data items and then they proceed to check damage to their list of data items and
continually add to the damaged list.
The algorithm shown below illustrates one method in which damage assessment
can be done on the grouped nodes.
Damage Assessment Algorithm
1. IDS notifies the co-coordinator C agent about the intrusion.
2. Co-coordinator agent C notifies all the other agents A
i
(i = 1, 2, 3….n) about the initial set
of damaged nodes.
3. Set R
jA
= 0 for all agents. (Where j = Round number and A = Agent ID).
4. For all agents A
i
, check if damaged node present in list.
4.1. If ‘yes’:
4.1.1. Perform damage assessment.
4.1.2. Update damaged list.
4.1.3. Count number of nodes with external dependencies (D
A
).
4.1.4. Increment R
jA
.
4.1.5. Update D
A.
112

4.2. If ‘no’:
4.2.1. Count number of nodes with external dependencies (D
A
).
4.2.2. Wait on completion or round 1 of agents with damaged nodes.
4.2.3. While R
jA
< 1
4.2.3.1. Initiate agents.
4.2.3.2. Read damaged list.
4.2.3.3. Perform damage assessment.
4.2.3.4. Update damaged list.
4.2.3.5. Increment R
jA
.
4.2.3.6. Update D
A.
5. Initiate agents.
6. Read damaged list.
7. Perform damage assessment.
8. Update damaged list.
9. Check if last node reached.
9.1 If ‘yes’, update R
jA
to F.
9.2 If ‘no’, increment R
jA
, then repeat step 6.
10. End.
The damage assessment phase can be run pseudo-parallelly. In the first step, the
intrusion detection system (IDS) notifies the co-coordinator agent C about the initial
list of damaged nodes. At this point, execution of all transactions is stopped. A copy
of the system log is saved from the time of the notification till the time the last
transaction was executed. In the next step, the co-coordinator agent notifies all the
other agents about the initial set of damaged nodes. Since the grouping is done pre-
emptively, all agents check their respective lists for the presence of these damaged
nodes. The damage assessment further takes place in multiple rounds.
In the first round, the agents responsible for these initial set of damaged nodes run
in parallel to identify other nodes in their list that are damaged and update the
damaged list. They then update the round number R
jA
to 1. Once they are done, the
other agents read from the damaged list in parallel to determine which of their nodes
are damaged. The agents then update the damaged list as and when they identify a
damaged node in their respective group.
Once all the agents have read from and updated the damaged list, the same
protocol is followed again. All agents read from the damaged list in parallel and
update the damaged list with the damaged nodes. At the end of each step, agents also
check to see if the execution has reached the last node in its group. If so, the agent
updates R
jA
to F (finished). Else R
jA
is updated to the current round number and the
agent then proceeds to read from the damaged list again. All agents follow the steps
until they have finished assessing all nodes in their group.
An agent enters a dormant state when it determines that none of its nodes are
further dependent on any other data items belonging to other agents. At this point, it
can notify all the other agents that it has completed damage assessment on its list of
data items. This state is reached when all the agents enter F (finished) in the damaged
list.
Since grouping does not depend on the notifications from the IDS, it can be done
beforehand. As transactions are executing, an agent can almost immediately identify
the extent of propagation of damage amongst its data items based on their
dependencies. Furthermore, if the damaged node is present nearer to the top level of
the graph, a large set of nodes beneath the damaged node can be marked as damaged
113

and added to the damaged list. This in turn would help the other agents perform their
damage assessment faster as more comprehensive list of damaged nodes are available
to them.
3 Experiments and Discussions
In order to demonstrate the working of the grouping model described in the previous
section, a set of simulations were performed. The objective of each simulation was to
understand how grouping works under practical circumstances and also how it
enhances the efficiency of damage assessment. A variety of graphs were constructed
and various possible dependencies amongst nodes were taken into account. These
graphs were used to run the grouping algorithm and also determine how they assisted
damage assessment. The simulations were implemented using the Java 1.6.0
programming language.
This section illustrates the analysis of damage assessment on Graph 2 illustrated in
Figure 2. The damage assessment algorithm described in the previous section was run
on the graph in two scenarios. In the first scenario, the nodes were grouped based on
our grouping algorithm and in the second scenario, the nodes were grouped randomly.
The results of the total number of writes into the damaged list required to complete
damage assessment by agents were compared.
Fig. 2. Graph 2 and the grouping result.
The assumptions for our simulations are as follows. The initial set of damaged
nodes are identified by the IDS and broadcasted to the agents via the co-coordinator
agent. The number of agents assigned to the random groups generated for a given
graph is same as the number of groups generated by our grouping algorithm.
We considered six different cases in which the nodes are grouped amongst agents
randomly. Table 1 to Table 6 show the groups, nodes in each group that were
randomly assigned and the agent responsible for each group. The degree of
randomness was varied. Damage assessment was then performed on these groups and
the results obtained were then tabulated and compared with that of damage
assessment done with our grouping algorithm.
114
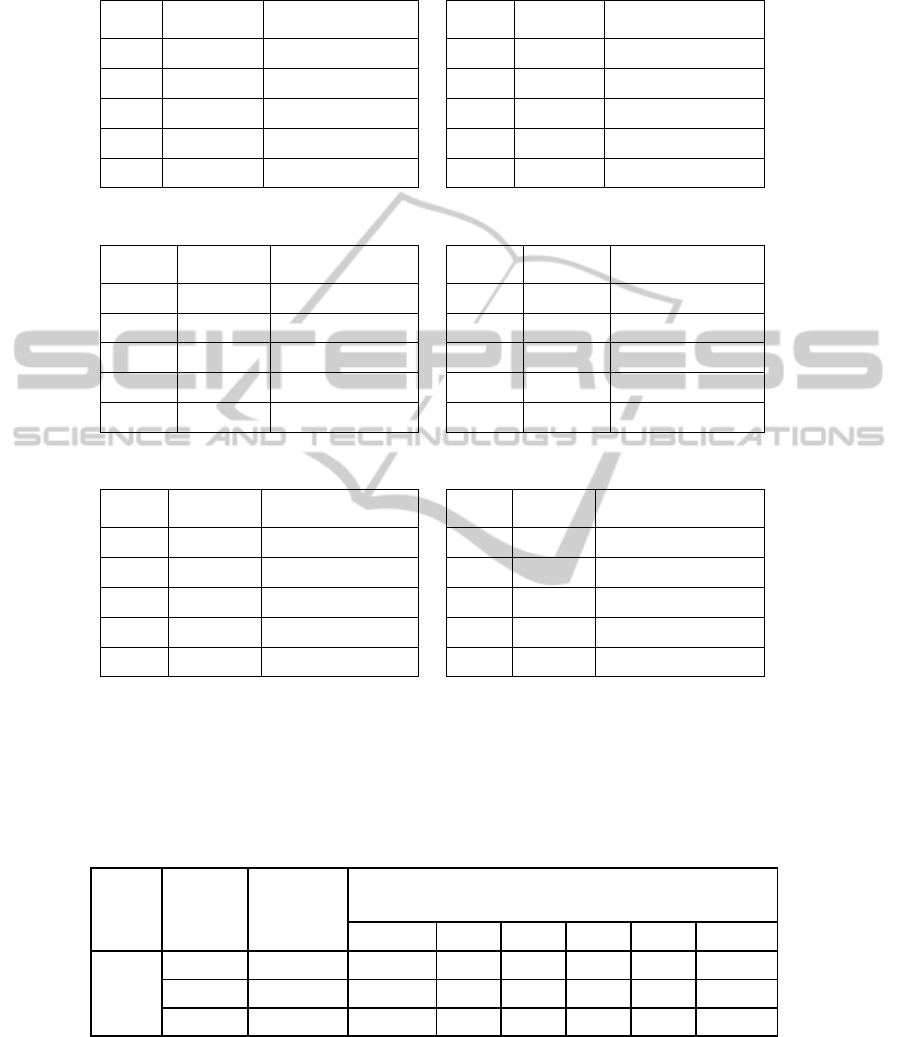
Table 1. Random node assignment case 1.
Group
assigned
Nodes Assigned
(Randomly)
A1 G1 1,2,6,7,8,22,23
A2 G2 10,11,13,20,21
A3 G3 3,4,5,9
A4 G4 12,24,25
A5 G5 14,15,16,17,18
Table 2. Random node assignment case 2.
Agent
Group
assigned
Nodes Assigned
(Randomly)
A1 G1 6,7,8,22,23
A2 G2 9,10,11,21
A3 G3 1,2,3,4,5,18,20
A4 G4 12,13
A5 G5 14,15,16,17,24,25
Table 3. Random node assignment case 3.
Agent
Group
assigned
Nodes Assigned
(Randomly)
A1 G1 4,6,13,22,23
A2 G2 9,10,11,21
A3 G3 12,5,18,20
A4 G4 1,2,3,14,15,
A5 G5 7,8,16,17,24,25
Table 4. Random node assignment case 4.
Agent
Group
assigned
Nodes Assigned
(Randomly)
A1 G1 12,14,15,16,18
A2 G2 1,2,3,9,10,11,17
A3 G3 13,23,24,25
A4 G4 4,5,6,7,8
A5 G5 20,21,22
Table 5. Random node assignment case 5.
Agent
Group
assigned
Nodes Assigned
(Randomly)
A1 G1 10,11,12,14,16,18
A2 G2 1,2,3,15,17
A3 G3 4,5,9,13,22
A4 G4 6,7,8,20,21
A5 G5 23,24,25
Table 6. Random node assignment case 6.
Agent
Group
assigned
Nodes Assigned
(Randomly)
A1 G1 4,12,14,15,16,17,18
A2 G2 1,2,3,5,6,7,8,9,13
A3 G3 20,21,22
A4 G4 23,24,25
A5 G5 10,11
Table 7 illustrates the results obtained. It can be seen that the nodes when grouped
based on our grouping algorithm greatly reduce the damage assessment latency. The
damaged list is generated in minimum possible writes. Also, it can be seen from Table
7 that our algorithm will not go into a state of deadlock while other grouping methods
suffer from this problem if the nodes are not assigned to the groups logically.
Table 7. Performance evaluation on graph 2.
Graph
Initial
damaged
nodes
Number of
writes (our
algorithm)
Number of writes (Random grouping) of the form m+nD (where
m = number of writes and nD number of agents in deadlock.
Case 1 Case 2 Case 3 Case 4 Case 5 Case 6
Graph 2
5 1 1 4+4D 5+5D 5+5D 5+5D 5+5D
4, 13 4 5 9 12 11 7 6
2, 15, 24 5 9 10 6+5D 7+3D 12 6+4D
115

4 Conclusions
The grouping model based on the longest-dependency-path-first approach proposed in
this research significantly reduces the damage assessment latency of the agent based
damage assessment process. Since grouping can be done in the background
irrespective of any notification of an intrusion from the IDS, once an intrusion has
been notified, we already have the groups ready. Thus the damage assessment process
takes less time. We have also developed an improved damage assessment algorithm
which takes advantage of the grouping mechanism presented here.
Acknowledgements
The work performed by Brajendra Panda has been supported in part by US AFOSR
under grant FA 9550-04-1-0429. We are thankful to Dr. Robert. L. Herklotz for his
support, which made this work possible.
References
1. Panda, B. and Giordano, J.: Reconstructing the Database after Electronic Attacks. In
Proceedings of the 12th Annual Working Conference on Database Security, Chalkidiki,
Greece (1998).
2. Reddy, K.: Agent Based Damage Assessment and Recovery. Masters Project, Department
of Computer Science and Computer Engineering, University of Arkansas, AR (2007).
3. Bernstein, P. A., Hadzilacos, V. and Goodman, N. Concurrency Control and Recovery in
Database Systems. Addison-Wesley, Reading MA (1987).
4. Elmasri, R. and Navathe, S. B.: Fundamentals of Database Systems, Second Edition.
Addison-Wesley, Menlo Park, CA (1994).
5. Gray, J. and Reuter, A.: Transaction Processing: Concepts and Techniques. Morgan
Kaufmann, San Mateo, CA (1993).
6. Korth, H. F. and Silberschatz, A.: Database System Concepts, Second Edition. McGraw-
Hill, New York (1991).
7. Ammann, P., Jajodia, S. and Liu, P.: Recovery from Malicious Transactions. IEEE
Transactions on Knowledge and Data Engineering, 14(5):1167-1185 (2002).
8. Lala, C. and Panda, B.: Evaluating Damage from Cyber Attacks. IEEE Transactions on
Systems, Man and Cybernetics, 31(4):300-310 (2001).
9. Tripathy, S. and Panda, B.: Post-Intrusion Recovery Using Data Dependency Approach. In
Proceedings of the IEEE workshop on Information Assurance and Security, NY (2001).
116
