Extension of Backpropagation through Time for Segmented-memory

Recurrent Neural Networks

Stefan Gl¨uge, Ronald B¨ock and Andreas Wendemuth

Faculty of Electrical Engineering and Information Technology, Chair of Cognitive Systems,

Otto von Guericke University Magdeburg, Universit¨atsplatz 2, 39106 Magdeburg, Germany

Keywords:

Recurrent Networks, Segmented-memory Recurrent Neural Networks, Backpropagation through Time,

Real-time Recurrent Learning, Information Latching Problem, Vanishing Gradient Problem.

Abstract:

We introduce an extended Backpropagation Through Time (eBPTT) learning algorithm for Segmented-

Memory Recurrent Neural Networks. The algorithm was compared to an extension of the Real-Time Recurrent

Learning algorithm (eRTRL) for these kind of networks. Using the information latching problem as bench-

mark task, the algorithms’ ability to cope with the learning of long-term dependencies was tested. eRTRL was

generally better able to cope with the latching of information over longer periods of time. On the other hand,

eBPTT guaranteed a better generalisation when training was successful. Further, due to its computational

complexity, eRTRL becomes impractical with increasing network size, making eBPTT the only viable choice

in these cases.

1 INTRODUCTION

Conventional Recurrent Neural Networks suffer from

the vanishing gradient problem in learning long-term

dependencies (Bengio et al., 1994). To overcome this

problem, the Segmented-Memory Recurrent Neural

Network (SMRNN) architecture fractionises long se-

quences into segments. In the end, the single seg-

ments are connected in series and form the ﬁnal se-

quence. The same procedure can be observed in hu-

man memorization, for instance, when people break

up long numbers like telephone or bank account num-

bers in digits, such that 4051716 becomes 40 - 51 -

716.

Yet, SMRNNs are trained with an extended Real-

Time Recurrent Learning (eRTRL) algorithm intro-

duced by Chen and Chaudhari (2009). The un-

derlying Real-Time Recurrent Learning algorithm

(Williams and Zipser, 1989) has an average time com-

plexity in order of magnitude O(n

), with n denoting

the number of network units in a fully connected net-

work (Williams and Zipser, 1995). Because of this

complexity, the algorithm is often inefﬁcient in practi-

cal applications where considerably big networks are

used. Further, the time consuming training makes it

difﬁcult to perform a parameter search for the optimal

number of hidden units, learning rate and so forth, for

a speciﬁc application, cf. (Gl¨uge et al., 2011).

In this paper we introduce an extension for the

Backpropagation Through Time (Werbos, 1990) al-

gorithm for SMRNNs, which we call extended Back-

propagation Through Time (eBPTT). Compared to

Real-Time Recurrent Learning, the Backpropagation

Through Time algorithm has a much smaller time

complexity of O(n

) (Williams and Zipser, 1995).

We compared both algorithms on a benchmark

problem designed to test the ability of the networks

to store information for a certain period of time. In

comparison to eRTRL we found eBPTT less capable

to learn the latching of information for long time peri-

ods. On the other hand, those networks that nonethe-

less were trained successful with eBPTT guaranteed

better generalisation, that is, higher accuracy on the

test set.

2 METHODS

The SMRNN architecture consists of two Simple Re-

current Networks (SRNs) (Elman, 1990) arranged in

a hierarchical fashion as illustrated in Fig. 1. The ﬁrst

SRN processes the symbol level and the second the

segment level of the input sequence.

451

Glüge S., Böck R. and Wendemuth A..

Extension of Backpropagation through Time for Segmented-memory Recurrent Neural Networks.

DOI: 10.5220/0004103804510456

In Proceedings of the 4th International Joint Conference on Computational Intelligence (NCTA-2012), pages 451-456

ISBN: 978-989-8565-33-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: SMRNN topology.

2.1 Forward Processing in SMRNNs

We use the receiver-sender-notation to describe the

processing in the network. The upper index of the

weight matrices refer to the corresponding layer and

the lower index to the single units. For example, W

denotes the connection between the kth unit in hid-

den layer 1 (x) and the ith unit in the input layer (u)

(cf. Fig. 1). Moreover, f

net

is the transfer function of

the network and n

, n

are the number of units

in the input, hidden 1, hidden 2, and output layer.

The introduction of the parameter d on segment

level makes the main difference between a cascade

of SRNs and an SMRNN. It denotes the length of a

segment, which can be ﬁxed or variable. The process-

ing of an input sequence starts with the initial symbol

level state x(0) and segment level state y(0). At the

beginning of a segment (segment head SH) x(t) is up-

dated with x(0) and input u(t). On other positions

x(t) is obtained from its previous state x(t − 1) and

input u(t). It is calculated by

(t) =











net



∑

k j

(0) +

∑

(t)



, if SH

net



∑

k j

(t − 1) +

∑

(t)



otherwise

(1)

where k = 1, . . . ,n

. The segment level state y(0)

is updated at the end of each segment (segment tail

ST) as

(t) =











net



∑

(t − 1) +

∑

(t)



if ST

(t − 1), otherwise

(2)

where k = 1,...,n

. The network output results in

forwarding the segment level state

(t) = f

net

∑

(t)

with k = 1,... ,n

(3)

While the symbol level is updated on a symbol by

symbol basis, the segment level changes only after d

symbols. At the end of the input sequence the seg-

ment level state is forwarded to the output layer to

generate the ﬁnal output. The dynamics of an SM-

RNN processing a sequence is shown in Fig. 2.

2.2 Extension of BPTT for SMRNNs

In the following, we describe how to adapt online

BackpropagationThrough Time to SMRNNs. That is,

the error at the output at the end of a sequence is used

instantaneously for weight adaptation of the network.

Learning is based on minimizing the sum of squared

errors at the end of a sequence of N segments,

E(t) =



∑

k=1

(t) − d

(t))

, if t = Nd

0, otherwise

(4)

where d

(t) is the desired output and z

(t) is the actual

output of the kth unit in the output layer.

The error is propagated back through the network

and also back through time to adapt the weights. Fur-

ther, it is not reasonable to keep the initial states

y(0) = f

net

(0)) and x(0) = f

net

(0)) ﬁxed,

thus, the initial activations a

(0) and a

(0) are also

learned. Here, the upper index of the activations re-

fer to the corresponding layer and a lower index to

the single units. For example, a

is the activation

at the kth unit in the hidden layer 2 that results from

connections from the hidden layer 1, which is simply

(t) =

∑

(t).

The gradient of E(t) can be computed from the

injecting error

(t) = z

(t) − d

(t). (5)

Using the back propagation procedure we compute

the delta error. The δ

(t) is a short hand for ∂E(t)/∂a

representing the sensitivity of E(t) to small changes

of the kth unit activation. The deltas for the output

units δ

, hidden layer 2 units δ

, and hidden layer 1

units δ

at the end of a sequence (t = Nd) are

(t) = f

′

net

(t))e

(t), (6)

(t) = f

′

net

(t))

∑

i=1

(t) (7)

(t) = f

′

net

(t))

∑

i=1

(t). (8)

At that point, we unroll the SMRNN on segment level

to propagate the error back in time. The state of the

hidden layer 2 changes only at the end of a segment

t = nd and n = 0,...,N − 1. Therefore, the delta error

for the hidden layer 2, and hidden layer 1 units results

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

452

Figure 2: SMRNN dynamics for a sequence of three segments with ﬁxed interval d. Processing on symbol level is described

by Eq. 1 and illustrated in the dashed squares. The segment level above, is processes as described by Eq. 2. Finally, Eq. 3

describes how the network output z is obtained for the sequence.

(nd) = f

′

net

(nd))

∑

i=1

((n+ 1)d), (9)

(nd) = f

′

net

(nd))

∑

i=1

((n+ 1)d). (10)

Once the computation was performed down to the be-

ginning of the sequence (t = 0), the gradient of the

weights and initial activation on segment level is com-

puted by

∆W

= δ

(Nd)y

(Nd), (11)

∆W

∑

n=1

(nd)y

((n− 1)d), (12)

∆W

∑

n=2

(nd)x

((n− 1)d), (13)

∆a

= δ

(0). (14)

For the adaptation of the weights on symbol level we

apply the Backpropagation Through Time procedure

repetitively for every time step τ = 0,...,d for every

segment of the sequence. That is, for the end of a

segment (τ = d)

(d) = f

′

net

(d))

∑

i=1

(d), (15)

(d) = f

′

net

(d))

∑

i=1

(d), (16)

and for τ < d we get

(τ) = f

′

net

(τ))

∑

i=1

(τ+ 1), (17)

(τ) = f

′

net

(τ))

∑

i=1

(τ+ 1). (18)

When the computation was performed to the begin-

ning of a segment (τ = 0), the gradient of the weights

and initial activation on symbol level is computed by

∆W

∑

τ=1

(τ)x

(τ− 1), (19)

∆W

∑

τ=2

(τ)u

(τ− 1), (20)

∆a

= δ

(0). (21)

Note that the sums in Eq. 13 and 20 start at n = 2

and τ = 2, respectively. This is due to the fact, that at

time t = 0 the hidden layer 2 has no input from hidden

layer 1 and further, hidden layer 1 has no input from

the input layer (cf. Fig. 2).

The computed gradients can be used right away to

change the networks weights and initial activations to

= W

− α∆W

+ η∆

′

(22)

with a learning rate α and the momentum term η. The

value ∆

′

represents the change of W

in the previ-

ous iteration. Figure 3 illustrates the error ﬂow in the

SMRNN for one sequence of length Nd.

2.3 Information Latching Problem

Typically dynamic systems change the output on cur-

rent or immediate past inputs. Nevertheless, it is of-

ten desired that even inputs that occurred much ear-

lier affect the system’s output. The information latch-

ing problem was designed to test a system’s ability

to model dependencies of the output on earlier inputs

(Bengio et al., 1994). In this context, “information

latching” refers to the storage of information in the

internal states of the system over some period of time.

The task is to distinguish two classes of sequences

where the classC of the sequence i

,...,i

depends

on the ﬁrst L items

C(i

,. .., i

) = C(i

,. .., i

) ∈ {0,1} with L < T

(23)

For our experiments the class-deﬁning start of a

sequence had a ﬁxed length of L = 50. To test the

ExtensionofBackpropagationthroughTimeforSegmented-memoryRecurrentNeuralNetworks

453

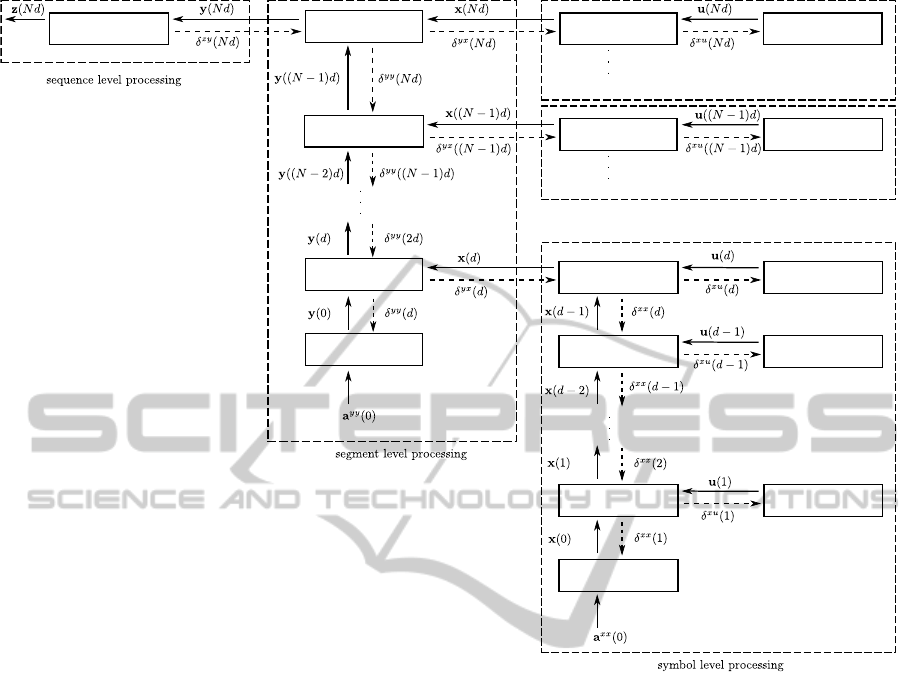
Figure 3: Errorﬂow of the eBPTT algorithm in an SMRNN for a sequence of length Nd. The solid arrows indicate the

development of the states of the layers in the network. The dashed arrows show the propagation of the error back through the

network and back through time.

networks ability to store the initial inputs over an arbi-

trary period of time, we gradually increased the length

of the sequence T. The sequences were generated

from an alphabet of 26 letters (a-z), such that the num-

ber of input neurons was 26 (1-of-N coding). A se-

quence was considered to be class C = 1 if the items

,...,i

match a predeﬁned string s

,...,s

otherwise it was class C = 0. All items i of a sequence

that were not predeﬁned were chosen randomly from

the alphabet.

For each sequence length T we created two sets

of sequences for training and testing. With increasing

length of the sequences T the set of training and test

samples was enlarged to ensure generalisation.

3 RESULTS

For every sequence length T we trained 100 networks

with eRTRL (Chen and Chaudhari, 2009) and eBPTT,

respectively. This was done to determine the algo-

rithms’ ability to learn the task in general. In every

epoch the sequences of the training set were shown in

a random order.

The networks’ conﬁguration and the size of the

training/test sets are adopted from (Chen and Chaud-

hari, 2009) where SMRNNs and SRNs are compared

on the information latching problem. Accordingly,

the SMRNNs are comprised of n

= 26 input units,

= n

= 10 units in the hidden layers, and one out-

put unit (n

= 1). Further, the length of a segment

was set to d = 15 and the sigmoidal transfer function

net

(x) = 1/(1 + exp(−x)) was used for the hidden

and output units. The input units simply forwarded

the input data which were ∈ {−1, 1}. Initial weights

were set to uniformly distributed random values in the

range of (−1,1).

Learning rate and momentum for each algo-

rithm were chosen after testing 100 networks on

all combinations α ∈ {0.1,0.2, . . .,0.9} and η ∈

{0.1, 0.2,...,0.9} on the shortest sequence T = 60.

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

454

The combinations that yielded the highest mean ac-

curacy on the test set were chosen for the experiment,

that is α = 0.1, η = 0.4 for eRTRL and α = 0.6,

η = 0.5 for eBPTT.

Training was stopped when the mean squared er-

ror of an epoch fell below 0.01 and thus, the net-

work was considered to have successfully learned the

task. For other cases training was cancelledafter 1000

epochs. Table 1 shows the results for eRTRL and

eBPTT for sequences of length T from 60 to 130.

The column for the number of successfully trained

networks (#suc) in Tab. 1 clearly shows a decrease

for eBPTT with the length of the sequences T. On

the other hand, nearly all networks were trained suc-

cessfully with eRTRL. Therefore, we can state that

eRTRL is generally able to cope better with longer

ranges of output dependencies than eBPTT.

The pure mean number of epochs (#eps) that were

needed for training is somewhat misleading. Over the

whole experiment eBPTT needs an average of 243.3

epochs for successful training while eRTRL needs

only 67.1 epochs. It is important to note that this does

not indicate that eRTRL training takes less time than

eBPTT. The high computational complexity of Real-

Time Recurrent Learning (O (n

)), and therefore also

of eRTRL, results in a much longer computation time

for a single epoch compared to eBPTT. This becomes

more and more evident with increasing network size.

Figure 4 shows the time that is needed to train an SM-

RNN for 100 epochs (T = 60, set size 50) depending

on the number of neurons in the hidden layers

. For

a considerable big network with n

= n

= 100 the

training took about 3 minutes with eBPTT and 21.65

hours with eRTRL.

0 200 400 600 800 1000

number of neurons in hidden layers n

= n

time for training in hours

eBPTT

eRTRL

Figure 4: Computation time for training depending on the

number of neurons in the hidden layers of the network.

Training lasted 100 epochs of 50 sequences of length T =

60.

Both algorithms were implemented in Matlab. Training

was done on a AMD Opteron 8222 (3GHz), 8GB RAM,

CentOS, Matlab R2011b (7.13.0.564) 64-bit.

The third column in Tab. 1 shows the performance

of successfully trained networks on the test set (Acc.).

For eBPTT we could observe higher accuracies than

for eRTRL. It is also reﬂected by the overall accuracy

of 96.8% for eBPTT compared to 89.2% for eRTRL.

This implies, that successful learning with eBPTT

guaranteed better generalisation.

4 DISCUSSION

Even though eRTRL was generally better able to cope

with the latching of information over longer periods

of time, the networks that ﬁnally learned the task with

eBPTT showed higher accuracies on the test set.

Altogether, the question which learning algorithm

to use for a speciﬁc task strongly depends on the char-

acter of the problem at hand. For small networks, as

used for the experiment in Tab. 1, the choice depends

on the timespan that has to be bridged. If we expect

the output to be dependent on inputs that are com-

paratively shortly ago (T = 60,.. . , 100) eBPTT pro-

vides the better choice. There is a high chance for a

successful training of the network with a good gen-

eralisation. When the outputs depend on inputs that

appeared long ago (T > 130), the eRTRL algorithm

provides the better solution. It guarantees a success-

ful network training where eBPTT could hardly train

the network.

In real world problems, as speech recognition,

handwriting recognition or protein secondary struc-

ture prediction the data to be classiﬁed has not such

a compact representation as the strings in the infor-

mation latching task. To be able to learn from such

data the network size, that is, number of processing

units, has to be increased. As shown in Fig. 4, eRTRL

becomes simply impractical for large networks (train-

ing time: 3 minutes with eBPTT in contrast to 21.65

hours with eRTRL / n

= n

= 100). In these cases,

eBPTT becomes the only viable choice of a training

algorithm.

In future, the combination of both learning algo-

rithms might be a possibility to overcome the draw-

backs of both methods. It could reduce the compu-

tational complexity of eRTRL and increase eBPTT’s

ability to learn long-term dependencies.

ACKNOWLEDGEMENTS

The authors acknowledge the support provided by

the Transregional Collaborative Research Centre

SFB/TRR 62 “Companion-Technology for Cognitive

ExtensionofBackpropagationthroughTimeforSegmented-memoryRecurrentNeuralNetworks

455

Table 1: Information latching problem with increasing sequence length T and ﬁxed predeﬁned string (L = 50). The size of

sets for training/testing was increased too. 100 SMRNNs with parameters n

= n

= 10, d = 15 were trained on each sequence

length. The number of networks that learned the task (#suc of 100) and the mean value of number of epochs (#eps) is shown

together with the mean accuracy (Acc.) of successful networks on the test set and its standard deviation (Std. Dev.).

T set size

eBPTT eRTRL

#suc #eps Acc. Std. Dev. #suc #eps Acc. Std. Dev.

60 50 79 230.6 0.978 0.025 100 44.3 0.978 0.025

70 80 58 285.7 0.951 0.047 100 63.9 0.861 0.052

80 100

61 215.2 0.974 0.024 100 66.2 0.862 0.088

90 150 48 240.4 0.951 0.123 100 52.4 0.940 0.044

100 150

43 241.4 0.968 0.018 100 82.1 0.778 0.065

110 300 36 250.0 0.977 0.049 100 69.6 0.868 0.052

120 400

17 305.4 0.967 0.050 100 56.7 0.950 0.040

130 500 14 177.6 0.978 0.017 96 101.4 0.896 0.078

mean 243.3 0.968 0.044 67.1 0.892 0.056

Technical Systems” funded by the German Research

Foundation (DFG).

REFERENCES

Bengio, Y., Simard, P., and Frasconi, P. (1994). Learn-

ing long-term dependencies with gradient descent is

difﬁcult. IEEE Transactions on Neural Networks,

5(2):157–166.

Chen, J. and Chaudhari, N. S. (2009). Segmented-memory

recurrent neural networks. IEEE Transactions Neural

Networks, 20(8):1267–1280.

Elman, J. L. (1990). Finding structure in time. Cognitive

Science, 14(2):179–211.

Gl¨uge, S., B¨ock, R., and Wendemuth, A. (2011).

Segmented-memory recurrent neural networks ver-

sus hidden markov models in emotion recognition

from speech. In International Conference on Neural

Computation Theory and Applications (NCTA 2011),

pages 308–315, Paris.

Werbos, P. (1990). Backpropagation through time: what

it does and how to do it. Proceedings of the IEEE,

78(10):1550 –1560.

Williams, R. J. and Zipser, D. (1989). A learning algo-

rithm for continually running fully recurrent neural

networks. Neural Computation, 1(2):270–280.

Williams, R. J. and Zipser, D. (1995). Gradient-based

learning algorithms for recurrent networks and their

computational complexity, pages 433–486. L. Erl-

baum Associates Inc., Hillsdale, NJ, USA.

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

456