Prediction of the Behaviours by the Prismatic Beams

with Polypropylene Fibers under High Temperature Effects

through Artificial Neural Networks

Fatih Altun and Tamer Dirikgil

Department of Civil Engineering, Erciyes University, Kayseri, Turkey

Keywords: Polypropylene Fiber, Concrete, High Temperature, Flexure Strength, Multilayer Perceptron, Radial Basis

Function Neural Network.

Abstract: In order to improve the mechanical qualities of a concrete, various kinds of fibers are added to the concrete.

In the studies, polypropylene (PP) fibers are employed as a fiber type. It has a significant place in the

researches that PP fibers not only improve the mechanical qualities of the concrete under normal

temperatures, but also prevents the bursting of the concrete with the internal vapour compression under high

temperatures. The distributions and locations of the fibers in the concrete and the variables employed for

experimental proceedings affect the mechanical results. This makes it difficult to link the obtained results to

each other. In order to establish a complicated link, it is inevitable to create a learning mechanism. In this

study, multilayered perceptrons (MLP) and radial basis function artificial neural network (RBFNN) models

were used and their flexure strengths were sought to be predicted. Both of the neural network models put in

a successful performance and enabled the prediction of the experimental results with a satisfying

approximation.

1 INTRODUCTION

It is practically not possible to empirically state the

effects of locations of the fibers, homogeneity of the

fibers and the different temperatures on the

mechanical qualities of a concrete. Therefore, it is

complicated to predict the behaviours of the concrete

with similar qualities by the data in hand. To model

and anticipate the complicated systems depending

on the input-output data and/or unknown behaviours,

methods to develop mathematical models in various

fields of civil engineering have been employed

(Astrom and Eykhoff, 1971).

In this study, bending tensile strengths of the

concrete with PP fiber addition are predicted using

the multilayered perceptron neural network and

radial basis function artificial neural network

models. For both of the models, the same input,

validation, and testing data were used. Addition of

split tensile strength obtained through experimental

studies to the variables on which experimental

proceedings were applied in the entry parameters

made it more difficult to link between the input-

output data. Ultimately, the performance of the two

different artificial neural network models was found

to be satisfying.

2 EXPERIMENTAL PROCEDURE

The samples produced during the experimental study

comprised of members with 40 MPa characteristic

compressive strength and in the C35/45 concrete

class (

TS EN 206/1, 2002). Samples were cured in

periods of 7,28 and 90 days and made ready. In

addition to the room temperature (24.5 ºC), five

more temperature effects of 100 ºC, 200 ºC, 400 ºC,

600 ºC and 800 ºC were employed. The samples

under the room temperature were assessed as the

reference samples for the other temperature effects.

Following the heating period, the temperature in the

oven was left to cool by itself with its lid closed until

it decreased to room temperature in order to keep the

experimental samples from exposing to the effects of

abrupt temperature changes. Table 1 and Table 2

shows the 216 cylinder and prismatic samples

according to each fiber type, volumetric fiber ratio,

and cure period and temperature value.

611

Altun F. and Dirikgil T..

Prediction of the Behaviours by the Prismatic Beams with Polypropylene Fibers under High Temperature Effects through Artiﬁcial Neural Networks.

DOI: 10.5220/0004114006110615

In Proceedings of the 4th International Joint Conference on Computational Intelligence (NCTA-2012), pages 611-615

ISBN: 978-989-8565-33-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

Table 1: Cyclindrical Samples.

Cyclindrical Samples (150x300mm)

Day

Temp.

(°C)

Polypropylene Fiber Ratio

(% Volumetrical)

FP ; MFP

0.0 0.1 0.2 0.3 0.4 0.5

28,

24.5 1 1 1 1 1 1

100 1 1 1 1 1 1

200 1 1 1 1 1 1

400 1 1 1 1 1 1

600 1 1 1 1 1 1

800 1 1 1 1 1 1

Total 2x6x3x6=216

Table 2: Prismatic Samples.

Prismatic Samples (150x150x750mm)

Day

Temp.

(°C)

Polypropylene Fiber Ratio

(% Volumetrical)

FP ; MFP

0.0 0.1 0.2 0.3 0.4 0.5

28,

24.5 1 1 1 1 1 1

100 1 1 1 1 1 1

200 1 1 1 1 1 1

400 1 1 1 1 1 1

600 1 1 1 1 1 1

800 1 1 1 1 1 1

Total 2x6x3x6=216

3 EXPERIMENTAL RESULTS

Addition of polypropylene fibers improved the

bending strength of the sample until 200ºC, but in

the samples that had been exposed to higher

temperatures, the change in the fiber ratio had no

contribution. With the increase in the cure period of

the sample, bending strength of the samples

increased. In the Figures 1-3 the bending strengths

of the prismatic samples for 7, 28 and 90 days are

given respectively.

Under high temperature values, bending strength

decreased also together with the increase in the fiber

ratio. Therefore, it can be stated that the local

caverns created by the melting PP fibers in the

sample adversely affect the behaviour of a member

when bending. The Multifilament Polypropylene

(MFP) fibers did not contribute to the bending

strengths of the samples under the room temperature

and 100 ºC as much as the Flament (FP) fibers did.

As the MFB fiber ratio increased, the bending

strength was observed to decrease. However, the

bending strength of the samples with MFP above

200ºC temperature values was measured to be higher

than those with FP fibers.

Figure 1: Flexural Strength of Prismatic Samples-7 Days.

Figure 2: Flexural Strength of Prismatic Samples-28 Days.

4 ARTIFICIAL NEURAL

NETWORK MODELS

For the prediction of the experimental data obtained

from the study, MLP artificial neural network model

and RBF neural network models were used.

Considering the error values and determination

coefficients between the observed and predicted

data, the performance of the models were evaluated

together.

In the first place, the experimental parameters to

be used in the models were identified and then the

training, validation and testing data were classified.

A total of 512 samples with different fiber types,

fiber ratios, and cure periods and which were

exposed to different temperature effects were

evaluated. Of the 512 samples, 216 were cylinder

samples with a size of 150x150x300 each and the

other 216 were prismatic samples with a size of

150x150x300mm each produced with the same

concrete mixture. Therefore, in the applications,

evaluations were made for the compression strengths

of 216 cylinder samples and the bending tensile

strength of the prismatic samples with the same

materialistic qualities.

In each model, considering the same input

parameters, 5 input parameters were used. Under the

light of these data, the prediction for 1 output

parameter was made and its error ratio and

correlations were evaluated. The input parameters

were set as the fiber type used to prepare the sample

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

612

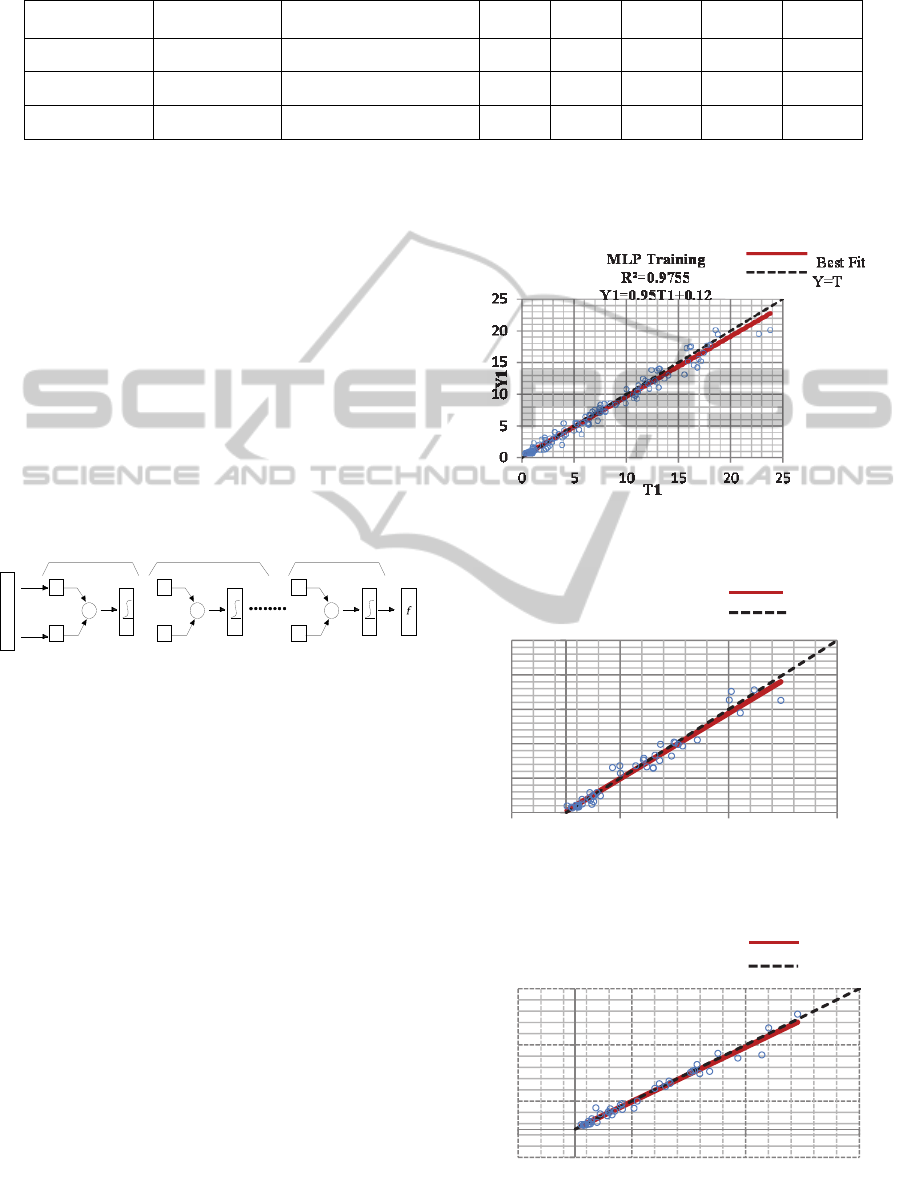
Table 5: Error values for MLP performance.

Hidden Layer

Number of first

layer neuron

Transfer Function

MSE RMSE MAE MARE

3 6 tansig-logsig-logsig-tansig 0.9734 0.6990 0.8361 0.5594 14.7446

5 logsig-logsig-tansig 0.9804 0.5099 0.7140 0.5063 14.6786

1 6 tansig- logsig 0.9826 0.4614 0.6793 0.5095 18.4026

mixtures (Ft), the split tensile strength of the

cylinder samples (sfc), volumetric fiber ratio in the

mixture (FR), temperature (T), and cure period (Cp).

The output parameter is the bending strength of

the prismatic samples (Md). The 216 data used in

themodel were classified with random selection 60%

reserved for training, 20% for validation and 20%

for testing phases. In order to make the models learn

the same data and predict the same test data, the

same training, validation and testing data were used

in both models.

The data used in the artificial Neural networks

were normalized first and then scaled.

4.1 Multilayer Perceptron (MLP)

Figure 3: Example architecture for one of the MLP

models.

For the design of MLP model, the number of

neurons in the hidden layer, activation (transfer)

function and the learning algorithm are of

importance. In the study, the MLP neural network

model was created in three forms using 3,2 and 1

hidden layers (Figure 4). The table 5 shows the

transfer function between the input layer and first

two hidden layers and the transfer functions whereby

the best prediction results were obtained between the

input layer and hidden layers. The transfer function

for the output layer is called “purelin”. As for the

learning function, it is the “trainlm” function which

updates its tendency values and weights according to

Levenberg-Marquart optimization. “Trainlm” is a

very quick learning function but needs a great deal

of memory for analysis (Matlab Software, R2009b).

The Figures 4, 5, and 6 show the performance of

the model depending on the values predicted during

the training, verifying and testing phases and the

correlation between the targeted values

The Figure 7 presents the fluctuation graph

between the values obtained during the testing phase

and the targeted values.

Figure 4: MLP correlation of training.

Figure 5: MLP correlation of validation.

Figure 6: MLP correlation of testing.



a1=logsig(IW1,1p¹+b1)

IW1,1

IW2,1

LW5,1

INPUTLAYER

HIDDENLAYER(x3)

OUTPUTLAYER

a2=logsig(IW2,1q¹+b2)

R=5

log‐sigmoid log‐sigmoid log‐sigmoid

‐5 5 15 25

MLP Validation

R²=0.9552

Y2=0.95T2+0.18

‐5

‐5 5 15 25

MLP Testing

R²=0.9734

Y3=0.97T3+0.056

Best Fit

Y=T

Best Fit

Y=T

PredictionoftheBehavioursbythePrismaticBeamswithPolypropyleneFibersunderHighTemperatureEffectsthrough

ArtificialNeuralNetworks

613

Figure 7: Coherence between target and predicted values

for MLP.

4.2 Radial Basis Function ANN

(RBFNN)

30 neurons have been used in this model.

Figure 8: Typical Radial Basis Function ANN

(Alexandridis et al., 2012).

Table 6 shows the error values obtained from the

radial basis neural networks

Figures 9, 10 and 11 present the performance

depending on the correlation between the values

predicted during the training, verifying and testing

phases and targeted values.

Table 7 states the obtained results from the

models and experimental data. Moreover, Table 8

states the mean absolute errors between the real and

predicted values for each data.

Table 6: Error values for RBFNN performance.

RBFNN

Testing

MSE RMSE MAE MARE

0.9581 0.6456 0.8035 0.5572 14.5678

Figure 9: RBFNN correlation of training.

Figure 10: RBFNN correlation of validation

Figure 11: RBFNN correlation of testing.

Table 7: Obtained results from the models and

experimental data.

Model R

MSE RMSE MAE MARE

MLP

Testing

0.9734 0.5099 0.7140 0.5063 14.6786

RBFNN

Testing

0.9581 0.6456 0.8035 0.5572 14.5678

5 CONCLUSIONS

This study followed the transformations in the

mechanical qualities of the concrete with

polypropylene fiber addition when exposed to

temperature and evaluated this transformation via

artificial neural networks. The link between the

transformation in the split tensile strength, cure

period, fiber type and temperature parameters and

bending strength has been provided.

Both of the models performed well in predicting

the experimental data of the bending strength. The

single hidden layer used in the multi layered model

created a fairly good correlation between the data.

However, as the error margin for predicting the

small values within the target values was wide, mean

0204060

Target…

SizeofTestin

Flexural

Strength

‐5

0 5 10 15 20 25

RBFNNTraining

R²=0.9855

0 5 10 15 20 25

RBFNNValidation

R²=0.9750

Y2=0.98T2+0.13

0 5 10 15 20 25

RBFNNTesting

R²=0.9581

Y3=0.94T3+0.46

Best Fit

Y=T

Best Fit

Y=T

Best Fit

Y=T

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

614

absolute relative error was found to be relatively

higher. When two hidden layers were used, smaller

MARE and MAE values were obtained. Three

hidden layers led to a decrease in the correlation and

to an additional increase in the errors. However,

error values were smaller than those in the single

hidden layered model. As the number of the hidden

layers increased, it caused the predictions to diverge

from the target as it increased the amount of weight

coefficients.

The mean absolute relative error values obtained

from the radial basis function neural network model

were lower. As such, it can be said that the model is

more successful in predicting the small target values

with less errors. However, the higher numbers of

mean absolute and square errors implicates that the

performance of the model was a little bit worse. As

the data to be predicted by the models were

randomly arrayed, there occurred an abrupt increase

or decrease between the previous values and the

following values. These changes led to a decrease in

the prediction performance and an increase in the

model errors. The error ratios of the radial basis

network resulting from these abrupt data changes

were lower than the multilayered network.

Both of the neural network models used in this

study performed successfully and enabled the

prediction of experimental values with satisfying

approximation.

ACKNOWLEDGEMENTS

Experimental part of this study was supported by

Scientific Research Project Units of Erciyes

University. (FBY-471)

Some part of this study was supported by

Scientific Research Project Units of Erciyes

University. (FBA-11-3462)

REFERENCES

Alexandridis, A., Triantis, D., Stavrakas, I., Stergiopoulos,

C., 2012. A neural network approach for compressive

strength prediction in cement-based materials through

the study of pressure-stimulated electrical signals.

Construction and Building Materials, vol. 30, pp.

294–300.

Astrom, K. J., Eykhoff, P., 1971. Automatica 7, pp. 123–

162.

Matlab R2009b, 2009. The Mathwork Inc. Company,

Massachusetts, U.S.A

TSI. TS EN 206/1, 2002. Concrete. Turkish Standards

Ankara. In Turkish.

PredictionoftheBehavioursbythePrismaticBeamswithPolypropyleneFibersunderHighTemperatureEffectsthrough

ArtificialNeuralNetworks

615