Factor Analysis and the Retrieval of Medical Images Depicting

Structures with Similar Shapes

Alexei Manso Correa Machado

Pontiﬁcia Universidade Catolica de Minas Gerais, R. Dom Jose Gaspar, 500, Belo Horizonte-MG, 30535-901, Brazil

INCT de Medicina Molecular, Faculdade de Medicina, Universidade Federal de Minas Gerais

Av. Alfredo Balena, 190, Belo Horizonte, MG, 30130-100, Brazil

Keywords:

Content-based Image Retrieval, Factor Analysis, Shape Representation, Medical Image Databases.

Abstract:

This work presents a new perspective to medical image retrieval based on factor analysis. The shape of

anatomical structures are represented as high-dimensional sets of vector variables obtained from non-rigidly

deforming a template image so as to align its anatomy with the subject anatomy of a group. By eliminating the

redundancy embedded in the data, a reduced set of factors is determined, corresponding to new variables with

possible anatomic signiﬁcance. The method’s ability to retrieve relevant images is exempliﬁed in a study of

the corpus callosum, a structure with very subtle shape differences. The factor analysis approach is compared

to principal component analysis in a set of 960 experiments, yielding signiﬁcantly higher precision rates.

1 INTRODUCTION

The development of modern medical imaging modali-

ties represents a corner stone for non-invasive analysis

of in vivo anatomy and physiology, as it provides in-

valuable information to support diagnosis and unveils

intricate mechanisms related to pathologies. Never-

theless, the overwhelming amount of information as-

sociated to these technologies cannot be appropriately

handled without computerized tools. Medical imag-

ing studies usually involve a large number of vari-

ables that by far exceeds the number of subjects in

the sample. In this scenario, the ability of physicians

to compare, analyze and select speciﬁc exams from a

database can be seriously compromised.

This article presents a new perspective to medi-

cal image retrieval based on multivariate factor anal-

ysis. The proposed method is based on the analy-

sis of high-dimensional sets of vector variables ob-

tained from non-rigidly deforming a template image

so as to align its anatomy with the subject anatomy of

a group, depicted by computerized imaging modali-

ties. By eliminating the redundancy embedded in the

data, we aim to extract a reduced set of common fac-

tors that correspond to new variables with possible

anatomic signiﬁcance. Image retrieval is performed

based on the computation of a similarity function that

takes into account the values assigned to each of the

factor variables, for both the dataset and the query.

Figure 1 shows a schematic of a content-based

image retrieval (CBIR) system that follows this ap-

proach. A set of images depicting neuroanatomical

structures is segmented and the structures represented

by their boundaries. Another image, taken as a com-

mon reference, is deformed through elastic registra-

tion so as to align its anatomy with the anatomy of

the images in the dataset. The result of registration

is a mapping function from each point in the refer-

ence to a point in the target image that enables de-

tailed shape description. The displacements are rep-

resented in a lower-dimensional space determined by

factor analysis and the corresponding transformation

coefﬁcients, called loadings, are stored to be used in

the retrieval step. The querying phase follows the

same steps used to convert the images into descriptive

scores. The query image converted to the correspond-

ing score vector is compared with the database, the

most similar images are retrieved and presented to the

user.

2 RELATED WORKS

The effective and efﬁcient representation of similar

shapes has been an old aspiration of the computer vi-

sion research community. Unlike gross scalar features

such as area, perimeter and compactness, the descrip-

tion of shape requires more complex sets of variables.

175

Machado A..

Factor Analysis and the Retrieval of Medical Images Depicting Structures with Similar Shapes.

DOI: 10.5220/0004116901750180

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2012), pages 175-180

ISBN: 978-989-8565-29-7

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

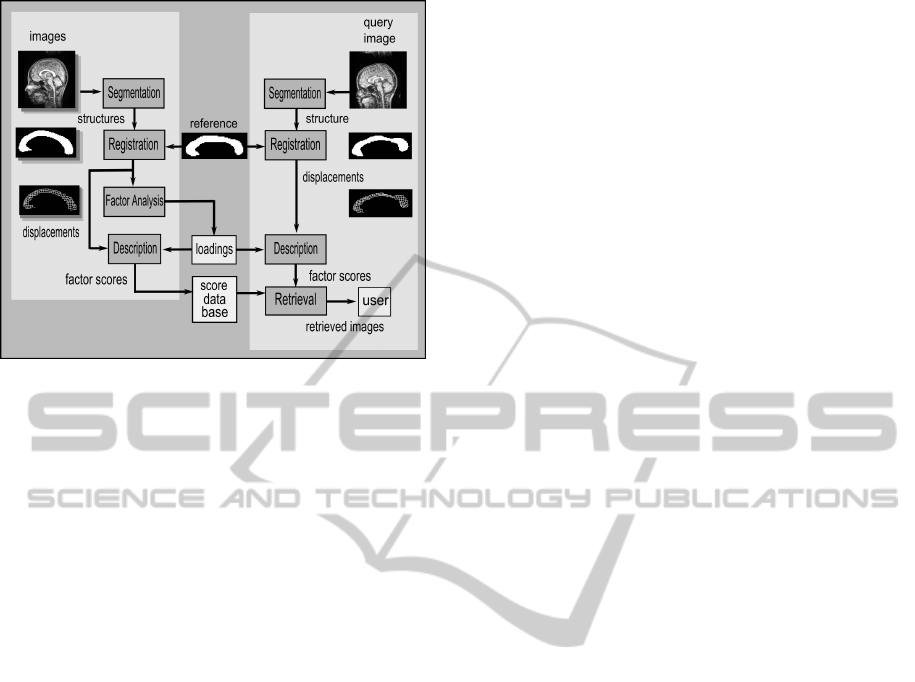
Figure 1: Schematic of a CBIR system based on registra-

tion. The left part of the scheme shows the steps performed

off-line for each image in the database. The on-line part of

the retrieval process is shown in the right. The link between

the on-line and off-line phases is the reference image that

is registered to the query and to the database, establishing a

basis for shape comparison.

Historically, the ﬁrst attempt to represent shape was

based on the explicit selection of landmarks. Land-

mark techniques assume that the relevance of the vari-

ables to be selected is known in advance, thus limiting

the robustness of automatic algorithms (Bookstein,

1997). An alternative to manual data selection is the

implementation of automatic registration algorithms

that enable more detailed shape description (Golland

et al., 2001; Attalla and Siy, 2005).

The representation of shape has been frequently

addressed as a data reduction problem. Multivari-

ate analysis based on principal components (PCA) is

one of the most frequently used method to describe

shape variability. It can be found in the early works of

Sclaroff and Pentland (1995) and Cootes and Taylor

(1999), applied to features and landmark data analy-

sis, and in the works of Le Briquer and Gee (1997),

which extends PCA to the high-dimensional sets of

variables resulting from registration. PCA and its

two-dimensional version are frequently used to the

recognition and retrieval of faces (Mohammed et al.,

2011) and biomedical images (Oliveira et al., 2010).

An alternative linear Gaussian model to PCA is

factor analysis (FA), which aims to explore the cor-

relation among the variables. When applied to shape

representation, FA may reveal aspects about the rela-

tionship between regions of interest and facilitates in-

terpretation. Nonetheless, the use of FA in shape rep-

resentation has been restricted to the representation

of gross measurements and landmarks, regardless of

exploring the relationship between pointwise shape-

related variables, as the ones obtained from image

registration (Reyment and J

oreskog, 1996; Machado

et al., 2004).

The retrieval of images based on their content is

still a challenge. Lew et al. (2006) presents a compre-

hensive discussions on the main aspects of image re-

trieval. Muller et al. (2004) and Iakovidis et al. (2009)

show how CBIR systems can be used to retrieve im-

ages in general medical databases. Shape-based re-

trieval systems relies on the concise and effective rep-

resentation of the objects’ contours (Zhang and Lu,

2004; Shu and Wu, 2011) or skeletons (Xie et al.,

2008), as well as on methods that allows for shape

matching and the deﬁnition of similarity metrics (Xu

et al., 2009; Biswas et al., 2010).

Image retrieval is even more challenging when the

database to be searched is composed of images de-

picting objects of the same class, with uniform shape

and subtle differences, as in the case of biomedical

imaging (Mallik et al., 2010). In the next sections we

discuss how factor analysis can be used to reduce the

dimensionality of complex shape representation and

allow for effective retrieval of images depicting struc-

tures with similar shapes.

3 METHODS

3.1 Image Registration

The images in the database should be registered to

a reference in order to establish a common basis

for comparison. Image registration can be stated as

the process of determining a correspondence between

each pixel in a reference image to a pixel in the sub-

ject image (Gee, 1999). The result of registration is a

displacement vector for each pixel. When a structure

does not present texture information, registration may

be applied to the boundaries, and thin plate splines

used to interpolate the warping to the whole structure,

so that each pixel in the reference image is assigned a

displacement vector.

3.2 Image Description

The overwhelming amount of information resulting

from image registration should be properly handled

as a data reduction problem. Factor analysis is a pow-

erful multivariate analysis method that explores the

correlation among the variables of a problem. Simi-

larly to PCA, it makes it possible to manage the high-

dimensional datasets obtained from imaging modali-

ties. A fundamental feature of FA is that, in addition

to data reduction, it may favor data interpretation.

KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

176

In PCA, the original p × N data matrix X com-

posed of N subjects at a p-dimensional centered vari-

able space is rotated in order to ﬁnd the orthogonal

axes along which the data is maximally spread out.

Data reduction is achieved by taking only the ﬁrst m

rotated variables (principal components). It can be

shown that the rotation matrix that causes the data to

align with the principal components is the orthogo-

nal m × p matrix B

whose rows are the eigenvectors

of the covariance matrix associated with the m largest

eigenvalues. The rotated data matrix Z is given by

Z = B

X. (1)

In factor analysis, the p × N data matrix Y com-

posed of N subjects at a p-dimensional standardized

variable space is represented as linear combinations

of m hypothetical constructs called factors:

Y = AF + E, (2)

where F is m × N matrix of common factors, E is the

matrix of unique factors which account for the por-

tion of Y that is not common to other variables, and

A is the p × m loading matrix. The coefﬁcients of A,

called loadings, express the correlation between vari-

ables and factors. The factor analytic model assumes

that common and unique factors are not correlated and

have null expected values. The covariance matrix for

the common factor is the identity matrix.

Considering the assumptions of the factor analytic

model, the variance of a given variable can be decom-

posed into components related to the common and

unique factors. Since AF and E are not correlated, the

covariance matrix of their sum is the sum of the co-

variance matrix of each term. Also, since cov(F) = I,

the relationship between the data covariance matrix,

S, and the covariance matrix of the unique factors, P,

can be written as

S = cov(AF +E) = cov(AF) + cov(E)

= Acov(F)A

+ P = AA

+ P.

(3)

Many techniques have been proposed to determine A.

The simplest one, called principal factor method, ne-

glects P and uses spectral decomposition to represent

the covariance matrix S:

S ≈ AA

= QLQ

= (QL

1/2

)(QL

1/2

)

, (4)

where L

1/2

is the diagonal matrix with the square root

of the m largest eigenvalues of S, and Q is the p × m

matrix of the corresponding eigenvectors. Therefore,

the loading matrix can be estimated based on the sam-

ple covariance matrix as

A = QL

1/2

. (5)

An important property of the loading matrix A is

that it can be rotated and still be able to represent

the covariance among factors and original variables.

The rotation of loadings plays an important role in

factor interpretation, as it is possible to obtain a ma-

trix that assigns few high loading for each variable,

keeping the other loadings small. The quartimax al-

gorithm (Reyment and J

oreskog, 1996) is an orthog-

onal rotation method that maximizes the variance of

the squared loadings in each column of the loading

matrix, so that each variable presents high loading for

fewer factors.

Once the linear coefﬁcients are determined (and

rotated, in the case of FA), we may want to repre-

sent the original dataset in the new lower-dimensional

variable space. This is done by computing the prin-

cipal component scores, Z, and factor scores, F, for

each subject in the sample. In PCA, Z is directly com-

puted from (1). In FA, F can be computed based on

(2), replacing the loading matrix A by its rotated ver-

sion R = AT, where T is the m × m orthonormal ma-

trix determined by the quartimax algorithm. We also

desire that the common factor scores, F, maximally

represent Y, so that the speciﬁc factors may be mini-

mized in a mean squared sense. The factor scores can

thus be obtained by solving the overdetermined linear

system Y = RF, viz.,

F = R

−1

Y. (6)

3.3 Image Retrieval

In a CBIR system based on image registration, the

user presents an image as a query, which is registered

to the reference image. The features obtained from

the resulting mapping function are compared to the

features of the images stored in the database, which

have been previously processed and registered to the

same reference. Following a measure of similarity,

the most similar images are retrieved and presented to

the user. In this work, the metrics used to determine

the similarity between two images were the Euclidean

distance and the cosine of the angle between their cor-

responding vector representation in the factor space

(Lew, 2010).

The effectiveness of an image retrieval system can

be evaluated by computing two metrics: The recall of

the system is the ability to retrieve relevant images.

It is deﬁned as the ratio between the number of re-

trieved images considered relevant and the total num-

ber of relevant images in the database. The precision

reﬂects the ability of the system to retrieve only rel-

evant images. It is deﬁned as the ratio between the

number of retrieved images considered relevant and

the total number of retrieved images. The plot of re-

call × precision for the results of a query gives an

estimate of the effectiveness of a CBIR system, as a

FactorAnalysisandtheRetrievalofMedicalImagesDepictingStructureswithSimilarShapes

177

compromise between both performance metrics is ex-

pected. Since a CBIR system should be evaluated for

a set of queries, an average precision value for each

level of recall is usually computed. Moreover, a sin-

gle average precision value for all queries, computed

based on all levels of recall is of interest, as it provides

a simple way to compare the performance of different

approaches.

4 EXPERIMENTS

The ability of the proposed CBIR system to retrieve

images from large homogeneous datasets is illustrated

with a case study on the morphology of the corpus

callosum, the largest bundle of axons connecting the

two hemispheres of the brain, whose shape variation

is related to many degenerative and genetic deseases.

The MRI images used in the experiments are a set of

299 patients and normal controls recruited for a study

on schizophrenia. The images were divided into 4

groups: one composed of a single subject used as a

reference for registration; 6 subjects of varying shapes

used as queries; 50 subjects used to evaluate the pre-

cision of the system; and the remaining 242 subjects

used to compute the eigenvalues and the loadings for

the PCA and FA transformation models. The pro-

vided images had been previously segmented by su-

pervised thresholding for other studies. For each seg-

mented image, the boundary of the callosum was au-

tomatically determined using the Rosenfeld algorithm

for 8-connected contours and the pointwise curvature

of the callosum contour computed for each subject,

using the k-curvature metric (Gonzalez and Woods,

2002). Registration was performed, by aligning the

reference image to all 298 subject’s images of the

dataset through dynamic programming, based on the

elastic matching algorithm. Average registration time

was 2.9 s. All methods were implemented in IDL 7.0

and run in a 2.66 GHz Intel Quad Core 2 processor

computer with 4 GB of RAM, under Windows XP op-

erating system.

Centered data matrix X and the standardized data

matrix Y were formed by taking the x and y compo-

nents of the displacement ﬁelds obtained from regis-

tration, at each of the 2830 pixels of the callosal tem-

plate, in a total of 5660 variables for each of the 242

subjects. Data reduction was performed through PCA

and FA, based on different number of components.

The computational costs for the off-line steps, consid-

ering 12 components, were: 4.6 s for the eigendecom-

position of the data matrices; 0.5 s for the computa-

tion of the rotated loadings; 15 ms for the computation

of the PCA scores; and 16 ms for the computation of

(a)

(b)

Figure 2: Example of retrieval based on FA (a) and PCA

(b) considering 12 components and the Euclidean distance.

The ﬁrst structure in each image is the query. The remain-

ing structures, from left to right, top to bottom, are the 15

ﬁrst retrieved structures for each method. The structures

considered relevant by an expert rater are shown in black.

the factor scores.

The evaluation of the methods was based on the

response of a group of 10 voluntary raters selected

from staff, graduate and undergraduate students of the

university (3 females and 7 males; age 20-42), with no

previous training on neuroanatomy. The users were

asked to select up to 10 structures considered to be

similar to each of the 6 query images, from the set

of 50 candidate images randomly displayed in a sep-

arate chart. For each query, the 10 most voted images

were considered to be relevant. The average number

of votes per query ranged from 3.6 to 4.7. Addition-

ally, the evaluation of relevance was performed based

on the judgment of an expert, in order to evaluate the

impact of the user perception on the results. It should

be noticed that both the queries and the set of 50 im-

ages used in the evaluation step were excluded from

the data used to compute the eigenvectors and load-

ings.

An example of the results of image retrieval based

on FA and PCA, considering 12 components and the

Euclidean distance, is shown in Figure 2. The ﬁrst

structure in each image is the query. The remaining

structures, from left to right, top to bottom, are the 15

ﬁrst retrieved structures based on each method. The

structures considered relevant by the expert rater are

shown in black. It can be seen that FA was able to

provide much better precision than PCA, retrieving 7

relevant structures, while PCA could retrieve only 3.

The superiority of FA was observed throughout the

experiments. Figure 3 shows an average precision ×

KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

178

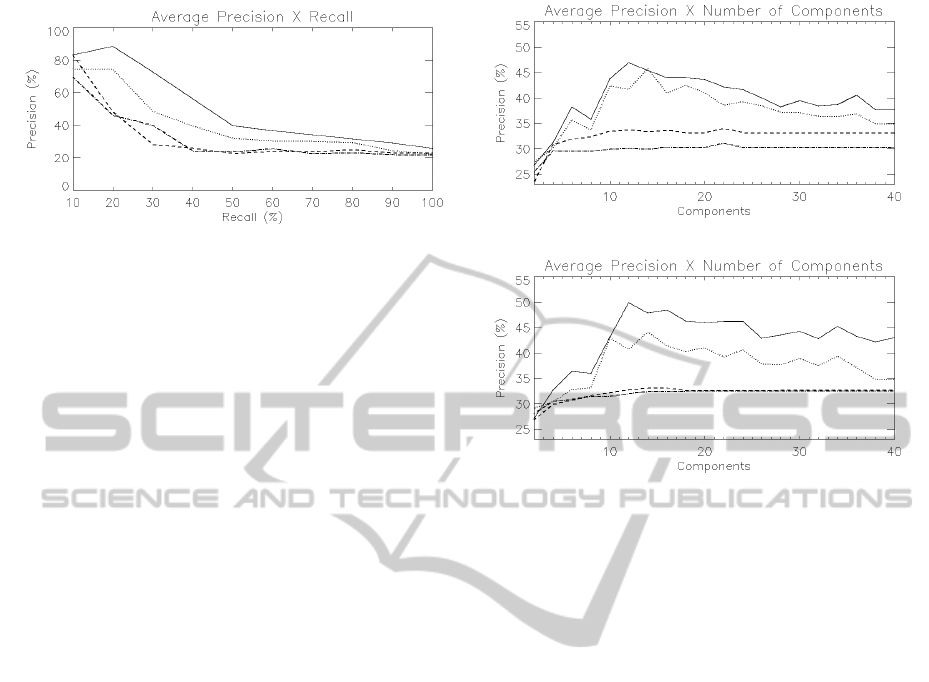
Figure 3: Average precision × recall plot considering 12

components and the Euclidean distance. The precision axis

shows an average of the precision for the 6 queries, at differ-

ent values of recall, based on FA for the expert (solid) and

for the group of raters (dotted), and based on PCA for the

expert (dashed) and for the group of raters (dash-dotted).

recall plot, computed over all queries, based on FA

and PCA for the expert rater and for the group of

raters. Regardless of the rater’s perception of similar-

ity, the FA representation was consistently more pre-

cise to retrieve relevant images, yielding 80% of av-

erage precision for 25% of recall, while PCA yielded

only 42%. The cost of the retrieval step, considering

12 components, was dominated by the computation

of the PCA scores (15 ms) and the FA scores (16 ms),

with other execution times being neglectably small.

The impact of parameter m (number of factors or

principal components) and the similarity metric was

investigated in a set of 960 experiments. The num-

ber of components varied from 2 to 40. The results

obtained with the Euclidean distance were generally

better than the ones obtained with the cosine metric.

The most effective number of components to repre-

sent the shape of the structure was around 12. Fig-

ure 4 summarizes the results in a plot of the overall

average precision as a function of the number of com-

ponents, based on the cosine metric and the Euclidean

distance. The precision axis shows an average of the

precision taken at all levels of recall and considering

all the 6 queries, based on FA and PCA for the two

groups of raters. The results of FA were consistently

superior to the ones based on PCA, regardless of the

similarity metric, number of components and user’s

perception, showing that the method should be seri-

ously taken into account while designing CBIR sys-

tems for the retrieval of similar shapes represented in

high-dimensional variables spaces.

5 CONCLUSIONS

A CBIR system based on factor analysis for the re-

trieval of medical images depicting similar-shaped

(a)

(b)

Figure 4: Overall average precision × number of compo-

nents plot considering the cosine metric (a) and the Eu-

clidean distance (b). The precision axis shows an average of

the precision taken at all levels of recall and considering all

the 6 queries, based on FA for the expert (solid) and for the

group of raters (dotted), and based on PCA for the expert

(dashed) and for the group of raters (dash-dotted).

structures was presented. The representation of the

images in the factor score space is advantageous as the

amount of information that should be accounted for

is drastically reduced. The method makes it possible

to manage the information obtained from image reg-

istration which is a pointwise displacement ﬁeld for

each image in the database. The correspondence of

these new variables to morphological features in the

structure is possible, since FA aims to represent the

correlation among original variables, instead of prin-

cipal modes of variance, as is the purpose of PCA.

The association of factors to shape variability con-

tributes to the retrieval effectiveness, as shown in the

experiments.

The method’s ability to retrieve relevant images

was exempliﬁed in a study of the corpus callosum, a

structure with very subtle shape differences. The fac-

tor analysis approach overperformed PCA in all sce-

narios. The relevance of the method relies in the fact

that it may serve as a sophisticated visual informa-

tion retrieval model for structures with complex shape

variability, in which small differences should be ac-

counted for.

The method deserves more systematic evaluation

with different structures and larger set of raters, as vi-

FactorAnalysisandtheRetrievalofMedicalImagesDepictingStructureswithSimilarShapes

179

sual perception is subjective and difﬁcult to quantify.

Relevance feedback is another important step to be

considered. Different similarity functions associated

to relevance feedback may enhance the effectiveness

of image retrieval, as the user’s preferences are more

rapidly met. The method’s ability to retrieve images

of the same group may qualify image retrieval as a po-

tential knowledge discovery tool. It implements new

levels of supporting environments and opens new per-

spectives to exploratory research in image databases.

ACKNOWLEDGEMENTS

This work was supported by FAPEMIG (PPM

00416/11), CNPq (481989/2010-2, 301907/2010-2)

and INCT-MM (FAPEMIG: CBB-APQ-00075-09 /

CNPq 573646/2008-2. The author is grateful to the

University of Pennsylvania for sharing the callosum

data.

REFERENCES

Attalla, E. and Siy, P. (2005). Robust shape similarity re-

trieval based on contour segmentation polygonal mul-

tiresolution and elastic matching. Pattern Recogn,

38(12):2229–2241.

Biswas, S., Aggarwal, G., and Chellappa, R. (2010). An

efﬁcient and robust algorithm for shape indexing and

retrieval. IEEE T Multimedia, 12(5):372–385.

Bookstein, F. L. (1997). Landmark methods for forms with-

out landmarks:morphometrics of group differences in

outline shape. Med Image Anal, 1(3):225–243.

Cootes, T. and Taylor, C. J. (1999). A mixture model for

representing shape variation. Image Vision Comput,

17(8):567–574.

Gee, J. C. (1999). On matching brain volumes. Pattern

Recogn, 32:99–111.

Golland, P., Grimson, W. E. L., Shenton, M. E., and Kiki-

nis, R. (2001). Deformation analysis for shape based

classiﬁcation. LNCS, 2082:517–530.

Gonzalez, R. C. and Woods, R. E. (2002). Digital Image

Processing. Prentice-Hall, Upper Saddle River.

Iakovidis, D. K., Pelekis, N., Kotsifakos, E. E., Kopanakis,

I., Karanikas, H., and Theodoridis, Y. (2009). A pat-

tern similarity scheme for medical image retrieval.

IEEE T Inf Technol B, 13(4):442–450.

Le Briquer, L. and Gee, J. C. (1997). Design of a Statistical

Model of Brain Shape. LNCS, 1230:477–482.

Lew, M., Sebe, N., Djeraba, C., and Jain, R. (2006).

Content-based multimedia information retrieval: State

of the art and challenges. ACM T Multimedia Comput,

2(1):1–19.

Lew, M. S. (2010). Principles of Visual Information Re-

trieval. Spring-Verlag, London.

Machado, A., Gee, J. C., and Campos, M. (2004). Structural

shape characterization via exploratory factor analysis.

Artif Intell Med, 30:97–118.

Mallik, J., Samal, A., and Gardner, S. L. (2010). A content

based image retrieval system for a biological speci-

men collection. Comput Vision Image Und, 114:745–

757.

Mohammed, A. A., Minhas, R., Wu, Q., and Sid-Ahmed,

M. A. (2011). Human face recognition based on mul-

tidimensional pca and extreme learning machine. Pat-

tern Recogn, 44:2588–2597.

Muller, H., Michoux, N., Bandon, D., and Geissbuhler, A.

(2004). A review of content-based image retrieval sys-

tems in medical applications-clinical beneﬁts and fu-

ture directions. Int J Med Inform, 73(1):1–23.

Oliveira, J., Machado, A., Chavez, G., Lopes, A., Deserno,

T., and Arajo, A. A. (2010). Mammosys: a content-

based image retrieval system using breast density pat-

terns. Comput Meth Prog Bio, pages 289–297.

Reyment, R. and J

oreskog, K. (1996). Applied Factor Anal-

ysis in the Natural Sciences. Cambridge University

Press, Cambridge.

Sclaroff, S. and Pentland, A. (1995). Modal matching for

correspondence and recognition. IEEE T Pattern Anal,

17(6):545–561.

Shu, X. and Wu, X. (2011). A novel contour descriptor

for 2d shape matching and its application to image re-

trieval. Image Vision Comput, 29:286–294.

Xie, J., Heng, P., and Shah, M. (2008). Shape matching

and modeling using skeletal context. Pattern Recogn,

41(5):1756–1767.

Xu, C. J., Liu, J. Z., and Tang, X. (2009). 2d shape

matching by contour ﬂexibility. IEEE T Pattern Anal,

31(1):180–186.

Zhang, D. S. and Lu, G. J. (2004). Review of shape repre-

sentation and description techniques. Pattern Recogn,

37:119.

KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

180