On the Design of Change-driven Data-ﬂow Algorithms and Architectures

for High-speed Motion Analysis

Jose A. Boluda, Pedro Zuccarello, Fernando Pardo and Francisco Vegara

Departament d’Inform`atica, Escola T`ecnica Superior d’Enginyeria, Universitat de Val`encia,

Avda. de la Universidad, S/N. 46100 Burjassot, Valencia, Spain

Keywords:

High Speed Motion Analysis, Bioinspired Visual Sensing, Data-ﬂow Architectures.

Abstract:

Motion analysis is a computationally demanding task due to the large amount of data involved as well as

the complexity of the implicated algorithms. In this position paper we present some ideas about data-ﬂow

architectures for processing visual information. Selective Change Driven (SCD) is based on a CMOS sensor

which delivers, ordered by the absolute magnitude of its change, only the pixels that have changed after the

last time they were read-out. As a natural step, a processing architecture based on processing pixels in a data-

ﬂow method, instead of processing complete frames, is presented. A data-ﬂow FPGA-based architecture is

appointed in developing such concepts.

1 INTRODUCTION

Motion analysis is an important issue in the ﬁeld of

computer vision, being the involved algorithms com-

monly based on the analysis of a sequence of still

images. This implies that most of the times there is

a large amount of data and the algorithms involved

are complex and time consuming. Researches have

focused their efforts onto improving the well-known

technology for acquiring images, or the computing

systems. Nevertheless, little effort has been put into

more innovative acquisition or computing approaches

to reduce this amount of calculus.

There are several different approaches for motion

analysis. From amongst them differential methods are

a type of motion analysis algorithm that typically in-

volves full image processing, where each image is a

snapshot taken at ﬁxed intervals. Typically, the nor-

mal procedure implies the application of several pre-

processing ﬁlters on the entire image and for each im-

age in the sequence. Next, some more complex pro-

cessing stages are applied. Whether there have been

many changes in the image, only a few, or even no

changes at all. The sequence of instructions is sys-

tematically applied to the entire image. No matter if

there is any new relevant information, being a waste

of time and energy.

Visual systems of living beings can offer smarter

solutions in the topic of image processing. The visual

system of most biological systems does not capture

images and send them sequentially to the brain at a

ﬁxed rate. The idea of a sequence of still snapshots

is not present in biological systems. Most biological

vision systems are based on different types of pho-

toreceptors that react to the light intensity delivering

its information asynchronously to higher levels of the

cognitive system (Gollisch and Meister, 2010).

A Selective Change Driven (SCD) camera deliv-

ers only the pixels that have changed since the last

read-out. A SCD sensor delivers only non-redundant

information, that is, information that has changed.

Moreover, pixel delivery is ordered by the absolute

magnitude of its change. Therefore, if there are time

constraints, the most signiﬁcant changes in the im-

ages will be processed, discarding minor variations.

Following this argumentation, it is possible to imple-

ment a data-ﬂow policy in the algorithm execution

with a conventional CPU, processing only those pix-

els that have changed. A pixel only triggers the in-

structions that depend on it. Moreover, it is possi-

ble to implement a custom data-ﬂow architecture for

processing only changing information. This strategy

will decrease the total amount of data to be processed,

speeding-up the algorithm execution.

In the literature there have been other approaches

which go beyond the limitations of frame-grabber vi-

sion systems. In (Mahowald, 1992) it is proposed

the ﬁrst silicon retina following Address-Event Rep-

resentation (AER) principles. Following this work,

many others have taken up the idea of replacing frame

548

Boluda J., Zuccarello P., Pardo F. and Vegara F..

On the Design of Change-driven Data-ﬂow Algorithms and Architectures for High-speed Motion Analysis.

DOI: 10.5220/0004120805480553

In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 548-553

ISBN: 978-989-8565-21-1

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

capturing, transmission and processing with single

pixel information (Higgins and Koch, 2000) (Chi

et al., 2007) (Lichtsteiner et al., 2008) (Camunas-

Mesa et al., 2010).

2 SCD SYSTEM AND

PROCESSING

A SCD system has as a main element a SCD camera,

and with this purpose, a new visual sensor which im-

plements the SCD behavior has been developed. The

sensor, built in CMOS technology, has a resolution

of 32x32 pixels and, although we assume this res-

olution is low for many applications, it is sufﬁcient

for demonstration purposes and can even be useful in

some cases.

In the SCD sensor every pixel works indepen-

dently of the others. A capacitor is charged, simul-

taneously for each pixel, to a voltage during an inte-

gration time. Every pixel has an analogue memory

with the last read-out value. The absolute difference

between the current and the stored value is compared

for all pixels in the sensor; the pixel that differs most

is selected using a Winner-Take-All circuit (WTA)

(Zuccarello et al., 2010) and its illumination level and

coordinates are read out for processing. It is impor-

tant to note that the concept of snapshot at instant t

can be kept, taking into account that all the photodi-

ode charges begin and ﬁnish at the same time. The

subsequent read-out order is performed by the WTA

circuit. All the sensor control signals are generated

with a 32-bit PIC microcontroller running at 80 MHz

which is connected to a computer through a USB link.

Further details about this new sensor, the camera and

its use in limited-resources systems can be found in

(Pardo et al., 2011).

2.1 SCD Algorithms

The design of image processing algorithms within the

SCD formalism requires a change in the way of think-

ing about how the programming instructions are ap-

plied to data. A more detailed explanation of how

to develop SCD algorithms can be found in (Boluda

et al., 2011).

A generic motion analysis algorithm can, many

times, be modeled as a pipeline of successive differ-

ent transformations to the image ﬂow: ﬁltering, fea-

ture extraction, etc. Between these processing stages

intermediate values are stored. Most of them can be

understood as intermediate images, but others can not

be viewable in a straight forward way, these images

being called intermediate images. Thus, each stage of

the image processing pipeline (except the ﬁrst which

has as input the initial pixel ﬂow) has as input full in-

termediate images and also produces full intermediate

images as output. No matter whether or not the initial

pixels or intermediates results have changed. All the

instructions at each stage are inevitably applied to the

data, even if they do not generate any change.

The SCD execution ﬂow is related with data-ﬂow

architectures: each new pixel ﬁres all the instructions

related with this new data. If there are no data changes

no instructions are ﬁred (and neither time nor energy

is consumed). Initially the SCD camera delivers those

pixels that have changed (gray level and coordinates).

Then the ﬁrst stage updates the contribution of this

new pixel value to its output intermediate images.

Following this idea all the stages do the same. When

new input data arrives at any intermediate stage, then

all the related instructions are ﬁred, updating the out-

put intermediate images.

The SCD sensor, as already mentioned, allows a

special way of ´non-accurate

functioning. As the pix-

els are read-out by the magnitude of their change, it

could be possible not to process all the changing pix-

els, but only the ﬁrst received pixels, which are those

that offer a greater variation. This behavior could be

desirable if there were computational time restrictions

and less accurate algorithm results could be accept-

able. Some experiments were been performed follow-

ing these ideas, simulating a SCD camera and apply-

ing this strategy to differential algorithms.

2.1.1 Linear Spatial Operators

Linear spatial operators are very common transfor-

mations used for preprocessing or feature extraction.

Spatial operators can be expressed as the systematic

application of a convolution mask to all the pixels of

the image. Let’s say that G is the result image of ap-

plying the M × M convolution mask w

i, j

to the image

I taken at instant t, then each G

x,y

pixel can be calcu-

lated as:

x,y

M−1

∑

1−M

M−1

∑

1−M

i, j

x+i,y+ j

(1)

where I

x,y

is a pixel of the image I.

With a SCD sensor, the way of computing the ﬁl-

tered image G is different. There will be a set of n

′

changing pixels that have been taken at the same time,

not a full input image. The G image must be changed

only with the contributionof the n

′

pixels. An individ-

ual I

x,y

pixel taken at instantt+1 contributesto M×M

pixels of G, thus this input must be updated adding the

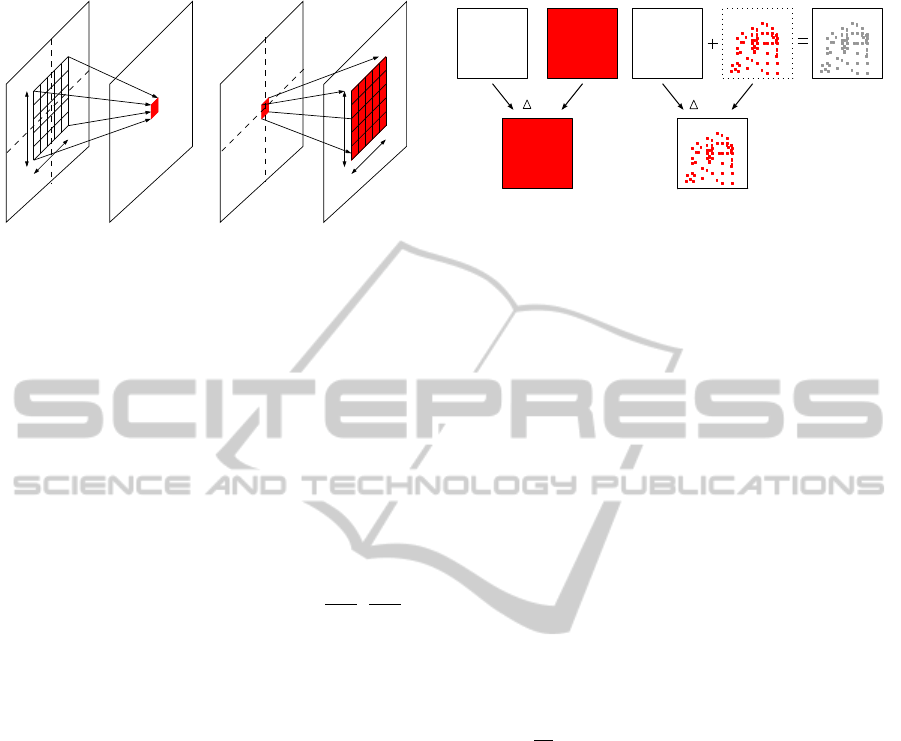
new value and removing the old one. Figure 1 shows

OntheDesignofChange-drivenData-flowAlgorithmsandArchitecturesforHigh-speedMotionAnalysis

549

Input

image I

Convolution

image G

(a) Classical spatial ﬁltering

image I

Input

image G

Convolution

(b) SCD spatial ﬁltering

Figure 1: Pixels involved in the computation of linear spa-

tial ﬁltering.

an example of the application differences of a con-

volution mask in the classical way (a) and the SCD

method (b). It seems that there is a growing number

of operations, but it must be noted that the number

of operations remains constant if all the pixels have

changed. As this scenario is the worst case, in general

there will be much less operations. In general, when

the SCD camera delivers the pixel I

x,y

in the instant

t + 1 the modiﬁed pixels in the G image are:

x+i,y+ j

= G

x+i,y+ j

−i,− j

x,y

(t+1)−I

x,y

(t)) (2)

∀ i, j ∈



1−M

M− 1



The difference between the new I

x,y

(t + 1) and the

old value I

x,y

(t) is performed as a ﬁrst operation. Af-

terwards, there are updated M

pixels of G.

It is possible to see how changing pixels trigger

the instructions that have a dependency with them.

This is the way SCD processing works. Only the

needed operations will be executed and no redundant

computations will be performed. In the case of spa-

tial dependency it is necessary to keep these interme-

diate images and write the modiﬁcation algorithms in

a data-ﬂow manner.

2.1.2 Temporal Processing

The implementation of temporal operators is essen-

tial for extracting motion from a video sequence. In

a simple classical implementation of a ﬁrst order dif-

ferentiation, at least two frames taken at different in-

stants are kept in memory, past and present images,

and an operator computes results taken into account

both images. When a third new complete image is

taken then there is a shift between these images, the

past image being replaced by the present image (al-

ready in memory) and the present image is replaced

by the new acquired image, this one becoming the

new present image. No matter how many changed

pixels are in a new image. The temporal operators

I(t) I(t+1)

I(t)

I(t) I (t+1)

x,y

I (t)

x,y

I(t)

Figure 2: Comparison between the classical implementa-

tion of the differential operator and the SCD implementa-

tion.

are applied even if there are no new computations to

make. In the case of a pipelined hardware implemen-

tation, all the pixels of all the intermediate images

stored as input for computing a derivative stage, must

be replaced.

Within a SCD camera the system works in a differ-

ent way. Now there are no more full-frame incoming

images. Afterwards, only a set of changing pixels (ac-

quired at the same time) are read out. Because these

pixels have been taken at the same time the concept

of instant can be kept and transformation to the SCD

formalism is relatively straight forward.

As an example, let I(t) be the past image and

I(t + 1) the present image in the video sequence. In

the classical approach, a temporal derivative can be

approached in the simplest way as the subtraction be-

tween both images, this operation being performed

for the n pixels in the image.



x,y

≈ ∆I

x,y

= I

x,y

(t + 1) − I

x,y

(t) (3)

Only the subtraction operation must be performed

for the n

′

read-out pixels, which are the changing pix-

els, in the SCD approach. Additionally, only the new

pixel I

x,y

(t + 1) must update the image I(t), replacing

the old value in the image. If this differentiation is

made with intermediate images the process is identi-

cal. A changing intermediate pixel triggers the updat-

ing in its temporal operator, the intermediate value be-

ing updated in the source image. More complex oper-

ators such as a second derivative can be discomposed

into simpler spatial and temporal derivatives. Figure

2 shows the comparison between the differential op-

eration using both the classical and the SCD methods.

In the case of a pipelined hardware implementation,

only the changing pixels of the intermediate images

stored as input for computing a derivative stage, must

be replaced.

Other functions, as are non-parametrictransforms,

are converted into the SCD formalism in the same

way. Each new pixel triggers the related operations,

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

550

taken into account its contribution into the result im-

age of each stage.

3 A SIMPLE MOTION

DETECTION ALGORITHM

A moving edges detection algorithm for showing the

SCD methodologyhas been implemented by software

(Boluda et al., 2011). The algorithm is very simple

and works only in structured scenarios. The idea of

this experiment was not to contribute to the motion

detection in terms of accuracy or robustness. The

main idea was just to show how the SCD approach can

accelerate an image processing algorithm. The algo-

rithm computes the mean velocity of a single object in

a scene by detecting its edges through a convolution

mask, and then calculating its temporal variation sub-

tracting them between two successive frames. If this

difference is greater than a certain threshold, depend-

ing on the scene, then this pixel is taken into account

as belonging to the object. Assuming a rigid object

with a translation movement, the velocity of the mov-

ing edges will coincide with the object velocity. Ve-

locity data (u, v) are available in this example when

the third image has been completely processed. Aft er

that, a new pair of velocity components will be avail-

able after each new image has been processed. The

response of the system for updating the value of the

(u, v) pair will be the acquisition time of a full image

plus its transmission time and the algorithm comput-

ing time for the whole image. No matter the number

of changes that have been produced in the image. All

the operations will be performed systematically for all

the pixels in the image.

3.1 Selective Change-Drive Software

Version

The SCD version of the algorithm described previ-

ously was written (by software) in a data-ﬂow man-

ner, following the rules described in this section. In

this version the SCD camera acquires an image at in-

stant t and sends the triplet: gray level intensity I

x,y

together with its coordinates (x, y), of the changing

pixels. As an extreme case, if there is not any moving

object, there will not be any gray level change, and

thus there will not be any delivered pixel and the sys-

tem will not process anything. In the other extreme

case, if all the intensity values have changed, all the

pixels will be sent and processed, giving no advantage

in terms of reduction of computations. Nevertheless,

it is shown experimentally that even with a high ra-

0 5 10 15 20 25 30

(a) SCD image

0 5 10 15 20 25 30

(b) Intermediate edges

image

0 5 10 15 20 25 30

ference image

Figure 3: Reconstructed images from the SCD data ﬂow.

tio of changing pixels, a valuable speed-up with the

SCD system is achieved. Details about the SCD im-

plementation in terms of pseudo code can be found in

(Boluda et al., 2011).

3.2 Experimental Results

They have been performed several experiments with

32x32 pixel simulated images and with the real pixel

ﬂow obtained from the SCD camera. First of all the

algorithm accuracy must be tested. That is, in a con-

trolled environment, and with images taken from a

conventional camera, the classical and the SCD algo-

rithm versions were tested. For the SCD version, the

data ﬂow was simulated from a conventional camera,

giving exactly the same results both algorithms.

Following, the system was checked with the SCD

camera. Figure 3 shows several images from the per-

formed experiment. Inthis experiment, a vertical strip

was placed over a small vehicle moving horizontally

from right to left. The scene may appear simple, but

with a 32x32 sensor complexobjects are not recogniz-

able and simpler geometric forms are ideal for testing

purposes.

The image shown in Figure 3 (a) is the accumula-

tive image that has been reconstructed by adding the

changing pixels delivered by the SCD camera. The

image is noisy, since strategies for correcting the im-

age quality in CMOS imagers (ﬁxed pattern noise,

etc.) have not been applied in order to show real im-

ages supplied by the SCD sensor. A simple Sobel ﬁl-

ter for the x coordinate transformed to the SCD for-

malism has been applied, as shown in section 2.1.1, to

implement the ﬁlter stage. The image shown in Figure

3 (b) shows edges correctly detected as well as some

spurious small edges corresponding to noisy pixels.

Finally, Figure 3 (c) shows the bynarized edges differ-

ence image from the last stages of the SCD algorithm.

From successive difference images, the velocity com-

ponents (u, v) are obtained as the center of mass of

the moving edges. There is some accuracy loss in

the velocity data due to the presence of noisy pix-

els that are contributing to the position of the object.

Nevertheless, the reasons for this loss of accuracy, due

to the use of real images, will be corrected in further

versions of the camera ﬁrmware, applying image im-

OntheDesignofChange-drivenData-flowAlgorithmsandArchitecturesforHigh-speedMotionAnalysis

551

10 20 30 40

Number of SCD images

SCD algorithm speed−up

Figure 4: Speed-up execution time of the SCD algorithm

versus the original implementation.

proving strategies for CMOS visual sensors.

Figure 4 shows the speed-up obtained with the

performed experiment by software. Clearly, the

speed-up will depend of the number of changing pix-

els. With fewer changing pixels, less redundant oper-

ations will perform the SCD algorithm compared to

the classical version and the algorithm speed-up will

increase. In the moving edge sequence, there is an

average of roughly 50% of pixels that change. There-

fore, we can see that we do not need a low quantity

of changing pixels to obtain a valuable speed-up with

this strategy.

Figure 4 shows the achieved speed-up with the

SCD algorithm versus the classical version, in func-

tion of the number of frames. The speed-up increases

with the number of images due that there is a ﬁxed

cost per image in the classical algorithm: compu-

tations are performed whether or not there are any

changing pixels and thus the related computations are

needed. This cost is always greater than the SCD al-

gorithm cost in each image. The speed-up asymp-

totically will approach the quotient between the cost

of both algorithms, original and SCD. This quotient

has been computed, giving a theoretical speed-up of

roughly 300. Therefore, Figure 4 really shows the ini-

tial part of an asymptote that, as the number of images

increases, approaches its speed-up to the ideal value

of 300. This speed-up depends on the experiment: ob-

jects velocity, illumination conditions, etc. A deeper

explanation and analysis of the moving-edge experi-

ment (in its software version) can be seen at (Boluda

et al., 2011).

4 HARDWARE VERSION

In this position paper we claim that the motion de-

tection algorithm in the SCD version can be im-

plemented into a data-ﬂow architecture, and this is

our current work: to implement all this ideas into a

hardware-based platform. All the experiments per-

formed until now have been made by software achiev-

ing, nevertheless, a valuable speed-up.

It must be considered that the SCD formalism is

a special case of data-ﬂow architectures, where each

incoming pixel change triggers the related operations.

Figure 5 shows a schema of the proposed pipelined

architecture, currently being developed into an AL-

TERA FPGA-based board. The pipeline has 5 stages,

having as input of the ﬁrst stage the SCD pixel ﬂow,

that is, the triplet formed by the grey level together

with their coordinates: (I, x, y). The output of the sys-

tem are the (u, v) velocity components.

The ﬁrst stage just updates the SCD image with

the pixels coming from the SCD camera. The SCD

image is stored in a 32x32 array of 1-byte registers.

The second stage is ﬁred when the new pixel replaces

the old one. This second stage computes the pixel

contribution of the new pixel to the convolution im-

age. The incoming pixel contributes to 8 pixels in the

convolution image following the equation 2, since the

chosen Sobel ﬁlter has a mask of 3x3 pixels.

Stage 3 stores changes into one of the two follow-

ing register banks. The update image at instant t has

information of the most important changes produced

at this instant, but also includes changes produced in

the past. Each time the camera acquires a new image,

the stage switches the storage bank. The older image

is replaced by the new one with the new pixels when

the updating of the newer frame has been ﬁnished.

Then the newer frame can be updated again with the

changes coming from the precedent stage.

Stage 4 reads the two frames and marks the corre-

sponding coordinate of a pixel pair (binarized image)

if the difference is greater than a certain threshold that

depends on the experiment. Stage 5 computes the

centre of mass of the contributing points and makes

the subtraction to the centre of mass of the preceding

image. The velocity components (u, v) are then deliv-

ered as the result of the algorithm.

5 CONCLUSIONS

In this position paper we propose a change-driven

processing architecture for image processing as an al-

ternative to full-frame processing systems. This al-

ternative will speed-up classical motion analysis al-

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

552

Stage 2

Convolution maskUpdate image

Stage 1 Stage 3

writing

Differential

Stage 4

Binarization

Stage 5

computation

Velocity

(I,x,y) (u,v)

SCD image

array of registers

Convolution

image image

Binarized

Image (t+1)

Image (t)

Figure 5: Data-ﬂow pipeline.

gorithms since it reduces the total amount of com-

putations performed. The recently developed 32x32

CMOS sensor delivers the changing pixels from the

present frame to the last sent frame at each integra-

tion time. Several theoretical studies following this

strategy were presented in the past with real images

constructed from the original SCD data-ﬂow. The

current paper presents some ideas for implementing

an already made SCD software implementation into a

FPGA-based platform.

There appear as a natural continuation to this ex-

periments performed by software, the principles of

data-ﬂow processing and architectures. Within these

architectures a pixel ﬁres the instructions that depend

on it, instead of following the imperative program-

ming model. The change-driven processing strategy

presented in this paper follows these ideas.

This kind of system is oriented to real-time image

processing, or systems that need very high speed pro-

cessing. The SCD strategy will deliver non-redundant

data, and the data-ﬂow processing system will per-

form, precisely, the needed computations, with the

lowest latency possible. Further versions of the SCD

camera ﬁrmware, and further sensors with greater res-

olution, will provide the potential for the implementa-

tion of much more complex and accurate algorithms

that will operate at the highest possible speed.

ACKNOWLEDGEMENTS

This work has been supported by the Spanish Govern-

ment project TEC2009-12980.

REFERENCES

Boluda, J., Zuccarello, P., Pardo, F., and Vegara, F. (2011).

Selective Change Driven Imaging: A Biomimetic Vi-

sual Sending Strategy. Sensors, 11(11):1100–11020.

Camunas-Mesa, L., Perez-Carrasco, J., Zamarreno-Ramos,

C., Serrano-Gotarredona, T., and Linares-Barranco,

B. (2010). On Scalable Spiking ConvNet Hardware

for Cortex-Like Visual Sensory Processing System. In

Proc. of the 2010 IEEE International Symposium on

Circuits and Systems, pages 249–252, Paris, France. .

Chi, Y., Mallik, U., Clapp, E., Choi, E., Cauwenberghs,

G., and Etienne-Cummings, R. (2007). CMOS cam-

era with in-pixel temporal change detection and ADC.

IEEE Journal of Solid-State Circuits, 42(10):2187–

2196.

Gollisch, T. and Meister, M. (2010). Eye smarter than sci-

entist believed: Neural computations in circuits of the

Retina. Neuron, 65():150–164.

Higgins, C. and Koch, C. (2000). A Modular Multi-Chip

Neuromorphic Architecture for Real-Time Visual Mo-

tion Processing. Analog Integrated Circuits and Sig-

nal Processing, 24(3):195–211.

Lichtsteiner, P., Posch, C., and Delbr¨uck, T. (2008). A

128x128 dB 15 µs latency asynchronous temporal

contrast vision sensor,. IEEE Journal of Solid-State

Circuits, 43(2):566–576.

Mahowald, M. (1992). VLSI Analogs of neural visual pro-

cessing: A synthesis of form and function. PhD thesis,

Computer Science Divivision, California Institute of

Technology, Pasadena, CA.

Pardo, F., Zuccarello, P., Boluda, J., and Vegara, F. (2011).

Advantages of Selective Change Driven Vision for

resource-limited systems. IEEE Transactions on Cir-

cuits and Systems for Video Technology, 21(10):1415–

1423.

Zuccarello, P., Pardo, F., de la Plaza, A., and Boluda, J.

(2010). 32x32 winner-take-all matrix with single win-

ner selection. Electronics Letters, 46(5):333–335.

OntheDesignofChange-drivenData-flowAlgorithmsandArchitecturesforHigh-speedMotionAnalysis

553