Supporting Mobile Robot’s Tasks through Qualitative Spatial Reasoning

Pascal Rost, Lothar Hotz and Stephanie von Riegen

HITeC e.V. c/o Fachbereich Informatik, Universität Hamburg, Hamburg, Germany

Keywords:

Qualitative Spatial Reasoning, Ontological Reasoning, Cognitive Robotics, Knowledge-based Systems

Applications.

Abstract:

In this paper, we present an application of qualitative spatial reasoning technologies for supporting mobile

robot tasks. While focusing on detection of interaction ability, we provide a combination of the spatial reason-

ing calculi RCC-8 and CDC as well as their integration with OWL-based ontologies. An architecture that uses

Prolog and complex-event processing implements our approach. We illustrate the results with a mobile robot

scenario in a restaurant.

1 INTRODUCTION

The focus of the research area cognitive robotics lies

on the usage of general logical representation and rea-

soning methods as well as ﬁnding appropriate tools

for manipulating and controlling robots in dynamic

and incompletely known worlds (Levesque and Lake-

meyer, 2007). Within this ﬁeld, qualitative spatial rea-

soning enables the representation and reasoning about

spatial conﬁgurations like The cup is on the counter or

The robot is near the guest. Speciﬁcally the abstrac-

tion that is provided via qualitative representations

facilitate effective and concise representations about

the quantitative environment of robots. This supports

robot’s tasks like the ability to interact with the envi-

ronment. From a cognitive point of view, human per-

ception of the environment also uses qualitative con-

cepts, notions, relations, and recall interrelationships

preferably in a qualitative manor.

Qualitative spatial reasoning can be used to ex-

plicitly represent spatial interrelations of regions

and/or objects. The practical use of this kind of rea-

soning and representation methods, especially for au-

tonomous mobile robots in an appropriate domain, is

an ongoing research topic, notably if all spatial di-

mensions (i.e. topology, orientation, and distance)

are to be considered (Renz and Nebel, 2007). Typ-

ically used spatial calculi tend to focus on one di-

mension (e.g. Region Connection Calculus (RCC)

(Randell et al., 1992) on topology and Cardinal Direc-

tion Calculus (CDC) (Goyal, 2000; Skiadopoulos and

Koubarakis, 2004) on orientation). Thus, the combi-

nation of qualitative spatial calculi of different dimen-

sions is necessary.

Ontologies can be used for representing the

knowledge of the robot about objects and the envi-

ronment. This allows domain knowledge (like ob-

jects and environment details) and application knowl-

edge (i.e. activities, like serving a meal to a guest

in a restaurant scenario) to be made explicit to the

robot. However, the combination and enhancement of

ontological reasoning with qualitative spatial reason-

ing is a difﬁcult task. Recent publications show that

the combination of these two reasoning and represen-

tation methods is coupled with losing the ability to

reason about spatial knowledge and revealing incon-

sistencies or to forfeit the decidability of ontological

reasoning (Katz and Grau, 2005; Hogenboom et al.,

2010a; Hogenboom et al., 2010b).

Hence, in this paper, we present a case study in

which we perform a combination of two qualitative

spatial calculi, i.e. Region Connection Calculus and

Cardinal Direction Calculus, with ontological repre-

sentations in a mobile robot scenario. We start with

the introduction of a concrete scenario in a restau-

rant environment, from which we extract technolog-

ical requirements that are needed by a robot fulﬁlling

speciﬁc tasks (Section 2). Then, we continue to pro-

vide a brief overview of applied representation tech-

niques, RCC, CDC, and ontological reasoning (Sec-

tion 3). In Section 4, we present our integrated ap-

proach that is evaluated by an implemented system

using Prolog (Wielemaker, J. et al., 2012), complex

event processing (Anicic et al., 2010), and the Web

Ontology Language OWL (Antoniou and Harmelen,

2003) (see Section 5). We close with a discussion

394

Rost P., Hotz L. and von Riegen S..

Supporting Mobile Robot’s Tasks through Qualitative Spatial Reasoning.

DOI: 10.5220/0004121803940399

In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 394-399

ISBN: 978-989-8565-22-8

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

(Section 6) and a summary in Section 7.

2 APPLICATION AREA AND

REQUIREMENTS

A versatile environment for demonstrating various

knowledge representation and reasoning techniques

for service robot tasks is the restaurant environment.

In this particular domain, it is required to represent

domain-speciﬁc objects, concepts, and rooms appro-

priately. Objects may be in use by guests or the robot

for certain reasons and can have (spatial and tempo-

ral) impacts on the environment. They might also

have hierarchical, temporal or spatial relations to each

other. Terminological knowledge is needed to distin-

guish dishes, drinks, meals etc. and their uses from

one another as well as to differentiate between areas

which may contain food products and seating areas.

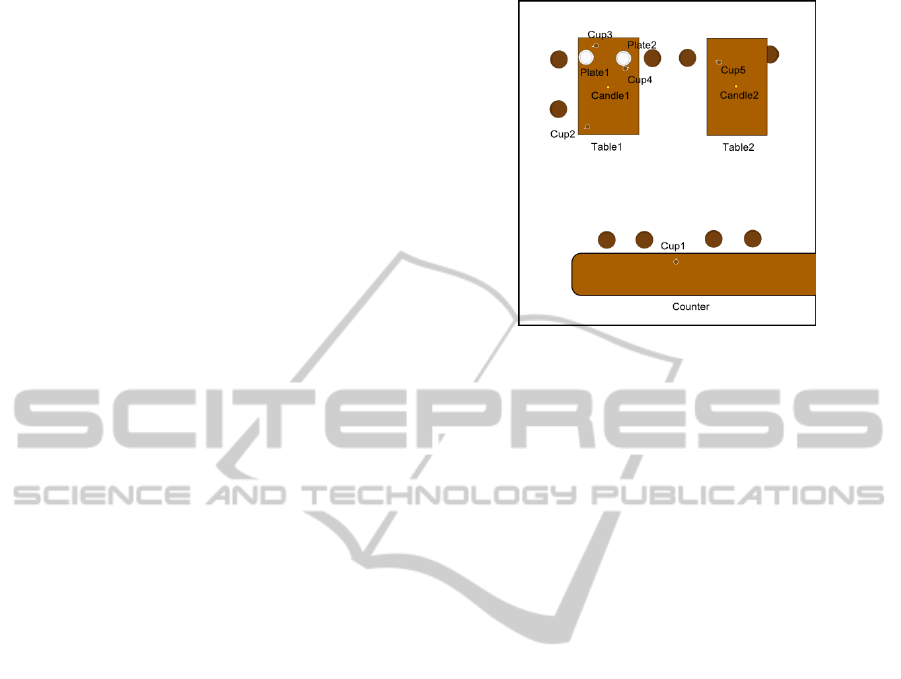
In our experiments, we investigate a ﬁctional restau-

rant layout as presented in Figure 1.

The concrete use cases considered in this paper

are typical waiter’s tasks like serving a beverage or

clearing a table. One speciﬁc task for example reads

as follows: “a robot shall take a cup from a counter

and carry it to a guest sitting at a table. The cup shall

be positioned in front of the guest and the robot shall

go back to the counter”.

In the following, some of the requirements are

listed that have to be fulﬁlled for processing the above

mentioned and likewise scenarios:

• The robot shall infer, if an own position is practi-

cal for placing a cup on the counter, i.e. to infer

whether the actual position is practical to interact

with a target object or not (interaction ability).

• The robot shall identify an ideal path to a table, i.e.

using the spatial conﬁguration of the environment;

the robot shall infer, if a certain place is reachable

and how the path looks like (global path-ﬁnding).

We focus on interaction ability and derive the

following technical requirements from the domain-

speciﬁc requirements, in this paper:

Knowledge Representation: Representation of do-

main and state knowledge with integration of

qualitative spatial calculi.

Consistency: Identifying inconsistencies in the

knowledge base and providing facts of a certain

situation, especially of spatial relationships.

Computation of Spatial Relationships: Inferring

unknown spatial relationships from known facts.

Figure 1: Detailed view of a ﬁctional restaurant environ-

ment equipped with counter, tables, cups, etc.

3 BACKGROUND

The basic techniques we combine in our approach are

qualitative spatial reasoning introduced in Section 3.1

and ontological reasoning introduced in Section 3.2.

3.1 Qualitative Spatial Reasoning

Spatial calculi allow to represent relations between

objects with ﬁnite sets of binary relations. Algorithms

can be applied to those representations to derive new

knowledge and check if a provided knowledge base

is consistent. RCC enables reasoning about topo-

logical properties of (abstract) regions. Especially

RCC-8 provides eight spatial relations disconnected

(DC), externally connected (EC), tangential proper

part (TPP), non-tangential proper part (NTPP), par-

tially overlapping (PO), equal (EQ), and the inverses

T PP

and NT PP

The Cardinal Direction Calculus (CDC) enables

reasoning about relative orientation between objects

by using the eight cardinal points (N, NE, E, SE, S,

SW, W, NW) as well as one further relation for repre-

senting direct neighborhood (i.e. bounding box, B).

The basic inference mechanism when using qual-

itative spatial calculi is based on the composition

operator ◦. Let D be a set of regions and R

, R

relations of the qualitative calculus: R

◦ R

{ (x R

z) | ∃y ∈ D : ((x R

y) ∧ (y R

z))}. Thus, a

composition operator computes the relations between

two regions x and z on the basis of a further region y

which is related to x and z. A composition table for a

certain calculus can be used to look up precomputed

(or manually resolved) results of all possible compo-

sitions (see (Li and Ying, 2003)).

SupportingMobileRobot'sTasksthroughQualitativeSpatialReasoning

395

For consistency computation, we map regions and

relations to a constraint net. A path-consistency algo-

rithms used for solving constraint satisfaction prob-

lems (Tsang, 1993) provides inference services like

identifying inconsistency (i.e. if no relation can be

computed between two regions) or restricting rela-

tions between regions to the only possible ones.

3.2 Ontological Reasoning

Ontological languages like OWL make it possible to

represent knowledge about objects, activities, rela-

tions etc. of a domain. Due to the formal repre-

sentation such ontologies provide, they are exchange-

able and, more importantly, can be used for inference

services. Description Logic reasoners (DL reasoner)

provide means for inference services like classiﬁca-

tion or instance checking (McGuinness, 2003). Ca-

pabilities for representation involve the separation of

instances (representing individual objects) and con-

cepts (as set of instances), taxonomic relations be-

tween concepts, and properties as an additional type

of relation among concepts. A TBox contains all con-

cepts whereas an ABox contains all instances.

However, the combination of OWL and qualitative

calculi is not straight forward. While some theoreti-

cal foundations for translating RCC-8 to OWL exist

(see (Grütter and Scharrenbach, 2009; Katz and Grau,

2005; Hogenboom et al., 2010a)) as well as some im-

plementations that include RCC-8 in a DL reasoner

(see (Stocker and Sirin, 2009)), we would like to use

both RCC-8 and CDC (for topology and orientation)

in a most enclosed fashion. Thus, this paper provides

an approach for integrating OWL, RCC-8, and CDC.

4 CONCEPTUAL APPROACH

For applying qualitative spatial reasoning in a mobile

robot environment as presented in Section 2, we de-

veloped the following approach.

4.1 Ontological Reasoning

To represent the domain knowledge, we use a TBox

with classes occurring in the environment (like cup,

plate, table, room etc.). An ABox is used to rep-

resent instances of concrete individual objects (like

table1, counter1 etc. (see Figure 1)). As object prop-

erties of OWL follow the same semantics as binary

relations, they can be used for representing qualita-

tive relations of the calculi. Thus, in the ABox an

Ob jectPropertyAssertion establishes a property (re-

lation) between two individuals. A fact like "The cup

is on the table, protrudes the table edge or touches the

edge or is completely on the table" will be expressed

as (Cup1, PO, TPP, NTPP, Table1), or the fact "The

table is north of the counter and east of the chair" may

be noted as (Table1 N Counter1, Table1 E Chair1)

(see Listing 1).

Listing 1: RCC-8 and CDC relations as properties of in-

stances.

Ob j ec t Pr o pe r ty A ss e rt i on (: PO : C u p 1 : T a b l e 1 )

Ob j ec t Pr o pe r ty A ss e rt i on (: TP P : Cup1 : Ta b l e1 )

Ob j ec t Pr o pe r ty A ss e rt i on (: NT P P : C up1 : Tab l e 1 )

Ob j ec t Pr o pe r ty A ss e rt i on (: N : T able1 : C o u n ter 1 )

Ob j ec t Pr o pe r ty A ss e rt i on (: E : T able1 : C h a i r 1 )

For computing the consistency of the provided

facts as well as the computation of all spatial rela-

tionships between objects in the environment, we use

the introduced calculi RCC-8 and CDC. We utilize

the machine readability as basic property of OWL to

automatically access ABox instances of the ontology.

Once we extracted the object instances and their re-

lations from the ABox we import them into a con-

straint system which uses the composition tables of

the calculi to achieve the mentioned inference tasks.

The constraint system uses the path-consistency al-

gorithm for making implicit spatial relations between

domain objects (instances) explicit. Newly found re-

lations may afterwards be imported into the ABox.

Thus, we combine the ontology with a qualitative spa-

tial constraint system instead of including spatial cal-

culi in a DL reasoner directly (this approach is similar

to Pellet-Spatial, see also (Bhatt et al., 2009)), how-

ever, with two calculi.

4.2 Interaction Ability

To detect the robot’s interaction ability, i.e. whether

the robot is able to interact with a given object at a

speciﬁc time or not, following subtasks need to be

performed:

1. The robot has to identify, if its tools, which will

be used for interaction, are in the direction of the

target object.

2. The robot has to check, if the target object can

be manipulated from the robot’s position and the

orientation of its tools.

3. The robot has to check, if the distance between

itself and the target object is appropriate for inter-

action.

4. The robot has to ensure that no hindering object is

in-between it and the target object.

Using the CDC one can ﬁnd cardinal points but

not the orientation. To be able to represent and exam-

ine the orientation of different agents and/or objects to

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

396

one another, we introduce a further instance that may

be inserted into the fact base representing the orien-

tation of the robot or any other object. One exam-

ple would be, if the orientation of the robot is north,

the direction would be represented by (Orientation N

Robot) whereas Orientation would be the artiﬁcially

added instance of the fact base. This allows not only

to fulﬁll the ﬁrst but also the second subtask: If the

robot’s orientation is equal to the inverse orientation

of the target object, one can assume that the needed

orientation for the interaction of the robot with the

target object is achieved.

To fulﬁll the third subtask, the computation of dis-

tance between the robot and the target object, quan-

titative spatial relations, which are not provided by

RCC-8 or CDC, are needed. However, for using these

calculi a mapping from quantitative acquired posi-

tions to qualitative relations will always be done be-

forehand. Otherwise, some of the RCC-8 relations

can not be applied between objects. For clariﬁca-

tion, if two objects are near to one another, a com-

putation step is needed that applies either the relation

EC or DC between these objects, dependent of the

actual quantitative distance. This implies that the spa-

tial conﬁguration of real world objects with RCC-8

relations inherently contains distance information. If

regions touch (EC), overlap (PO), or are contained in

the region of the robot (NT PP, T PP), the robot and a

target object are typically near enough to interact.

Considering obstacles as well, the previously

computed orientation and the inherent distance (CDC

and RCC-8 relations) can be used. Seen from the

topological angle, an object can only be between two

other objects, if the corresponding region of the object

is connected with the other two regions. Thus, using

RCC-8 one considers the robot’s region, the target ob-

ject’s region, and the region of a potentially obstacle

O. If O’s region is related to the other two regions

with the relation PO, NT PP, or T PP one can assume

that O is really an obstacle. With CDC an object O

might be an obstacle if, considered from the target

object, it is in the same direction like the robot is and,

considered from the robot, O is in the same direction

as the target object. For example, if the robot is east

of the target object (Robot E Target) (thus, also holds

(Target W Robot)), then an object that is also east of

the target and west of the robot might be in-between,

thus, might be an obstacle. However, such inference

might not be correct, because the calculi only consid-

ers two dimensions or the robot might ﬁnd a plan for

grasping the target although an object is in-between.

In summary, it is possible to evaluate the interaction

ability with spatial qualitative relations, although it

might be uncertain.

5 EVALUATION OF THE

APPROACH

For the evaluation of our conceptual approach, an

architecture was implemented that combines the

needed inference technologies. As underlying sys-

tem serves the Event Transaction Logic Inference

System (ETALIS) (Anicic, D. and Fodor, P., 2011),

that implements a complex event processing (CEP)

framework on the basis of Prolog. Event process-

ing enables the processing of continuous data streams,

which in our case are created through the sensors of

a robot. The use of Prolog allows not only the gen-

eration of complex events from simple events (like

it is possible with traditional CEP systems) but also

to make strong logically rooted conclusions and in-

ferences about the events, their context, or other for-

mulated predicates. In comparison to other CEP-

systems, which are implemented with procedural or

object-oriented languages, ETALIS is more ﬂexible

and has partially better performance results (Anicic

et al., 2010). Starting with ETALIS, we combine

it with the PROLOG-OWL interface THEA2 (Vas-

siliadis, V. and Mungall, C., 2012), and DL reason-

ers (like Pellet (Clark and Parsia, LLC, 2011), Racer

(Racer Systems GmbH Co. KG, 2011), or HermiT

(Motik, B. and Shearer, R. and Glimm, B. and Stoi-

los, G. and Horrocks, I., 2011)) to our system called

ETALIS-Spatial.

The knowledge representation of our system is re-

alized with an OWL2 knowledge base. Objects and

spatial relations are deﬁned as described in Section 3.

THEA2 enables access to the ABox for extracting and

including spatial relations and all instances for partic-

ipating objects.

Processing with ETALIS-Spatial starts from sen-

sor data, which is assumed to be already mapped

from quantitative values to qualitative values. The

input consists of identiﬁed objects and their direct

spatial relations. This preprocessing could also be

done in principal by the Prolog engine. Typical ex-

amples for input data (primitive events) are asser-

tobject(Plate1) for an recognized object, assertRela-

tion(Plate1, Plate2, DC) for establishing a spatial re-

lation, robotMoved, for a ﬁnalized movement of the

robot. A robotMoved event triggers the new com-

putation of spatial relations between the robot and

other objects. Such input is continuously streamed

into the system. After asserting a bunch of new data

the system starts a consistency test of the knowledge

base and furthermore infers new relations if possible

(marked e.g. as foundRelation(Plate2, Cup4, EC)).

Complex events represent the output of this computa-

tion, e.g. interactable(Plate2) for indicating that the

SupportingMobileRobot'sTasksthroughQualitativeSpatialReasoning

397

system detected an object with which the robot can

interact. These complex events can be used like prim-

itive events for further computations.

The system was tested with a scenario depicted in

Figure 1. In it, the system computes the interaction

ability of the robot with Plate2 from different posi-

tions resulting out of two different paths (see ﬁgure 2).

If the robot approaches Plate2 from south-east (solid

path), it computes that an interaction with Plate2 is

not possible because Cup4 is an obstacle. If the robot

approaches Plate2 from north (dotted path), it com-

putes that an interaction with Plate2 is possible be-

cause no other object hinders the interaction.

Figure 2: Path of the robot; dotted path A, solid path B.

In summary, the evaluation shows an implemen-

tation of our conceptual approach presented in Sec-

tion 4. The qualitative spatial relations can be rep-

resented in an ontology as properties. The knowledge

can be extracted from the ontology for processing in a

separate spatial Prolog-based reasoner. This reasoner

computes all spatial relations and detects interaction

ability between the objects. By using complex event

processing, a continuous stream of data could be pro-

cessed.

6 DISCUSSION

Our work shows that typical robot tasks can be sup-

ported by applying qualitative spatial reasoning. We

applied RCC-8 and CDC to cover topology and ori-

entation aspects of spatial reasoning. Relations of

these calculi could be integrated in an OWL-based

ontology for maintaining the needed knowledge cen-

trally. Computing new spatial relations and consis-

tency checks were performed by a Prolog system

based on composition tables provided by the calculi

in combination with path-consistency algorithms.

A ﬁrst implementation used the CEP-framework

ETALIS and enhances it to ETALIS-Spatial. We im-

plemented an ontology representing parts of a restau-

rant. In principle, such an ontology can be enhanced

for cover more facets of the tasks. Further or other

qualitative calculi which handle other aspects can be

integrated into the system by modeling their compo-

sition tables and relations in Prolog.

7 CONCLUSIONS

This paper demonstrates the application of the quali-

tative spatial calculi RCC-8 and CDC for robot tasks.

The approach combines these calculi with ontological

reasoning by modeling the relations in OWL but com-

puting spatial inferences with logical programming.

Thus, consistency checking and computation of new

spatial relations could be performed. An extension

of the complex event processing framework ETALIS

implements our approach. We demonstrate it’s use in

a restaurant scenario and could show how qualitative

spatial reasoning can support tasks of mobile robots.

ACKNOWLEDGEMENTS

This work is supported by the RACE project, grant

agreement no. 287752, funded by the EC Seventh

Framework Program theme FP7-ICT-2011-7.

REFERENCES

Anicic, D., Fodor, P., Rudolph, S., Stühmer, R., Stojanovic,

N., and Studer, R. (2010). A Rule-Based Language for

Complex Event Processing and Reasoning. In Hitzler,

P. and Lukasiewicz, T., editors, Web Reasoning and

Rule Systems, volume 6333 of Lecture Notes in Com-

puter Science, pages 42–57. Springer Berlin / Heidel-

berg.

Antoniou, G. and Harmelen, F. V. (2003). Web Ontology

Language: OWL. In Handbook on Ontologies in In-

formation Systems, pages 67–92. Springer.

Bhatt, M., Dylla, F., and Hois, J. (2009). Spatio-

terminological inference for the design of ambient en-

vironments. In COSIT, pages 371–391.

Motik, B. and Shearer, R. and Glimm, B. and Stoilos, G.

and Horrocks, I. (2011). Hermit OWL Reasoner.

http://hermit-reasoner.com/. Date: March, 6th 2012.

Clark and Parsia, LLC (2011). Pellet: OWL 2 Reasoner for

Java. http://clarkparsia.com/pellet. Date: March, 1st

2012.

Anicic, D. and Fodor, P. (2011). etalis - Event-

driven Transaction Logic Inference System.

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

398

http://code.google.com/p/etalis/. Date: February,

25th 2012.

Goyal, R. K. (2000). Similarity assessment for cardinal di-

rections between extended spatial objects. PhD thesis,

The University of Maine. AAI9972143.

Grütter, R. and Scharrenbach, T. (2009). A qualitative ap-

proach to vague spatio-thematic query processing. In

Terra Cognita (Terra2009).

Hogenboom, F., Borgman, B., Frasincar, F., and Kaymak,

U. (2010a). Spatial knowledge representation on the

semantic web. In Semantic Computing (ICSC), 2010

IEEE Fourth International Conference on, pages 252

–259.

Hogenboom, F., Frasincar, F., and Kaymak, U. (2010b). A

review of approaches for representing rcc8 in owl. In

Proceedings of the 2010 ACM Symposium on Applied

Computing, SAC ’10, pages 1444–1445, New York,

NY, USA. ACM.

Wielemaker, J. et al. (2012). SWI-Prolog - a comprehensive

Free Software Prolog environment. http://www.swi-

prolog.org/. Stand: 8. März 2012.

Katz, Y. and Grau, B. C. (2005). Representing qualitative

spatial information in owl-dl. In Proceedings of the

OWL: Experiences and Directions Workshop. Galway.

Levesque, H. and Lakemeyer, G. (2007). Cognitive

Robotics. In van Harmelen, F., Lifschitz, V., and

Porter, B., editors, Handbook of Knowledge Represen-

tation. Elsevier.

Li, S. and Ying, M. (2003). Region connection calculus: Its

models and composition table. Artiﬁcial Intelligence,

145(1

U2):121 – 146.

McGuinness, D. L. (2003). Conﬁguration. In Baader,

F., Calvanese, D., McGuinness, D. L., Nardi, D.,

and Patel-Schneider, P. F., editors, Description Logic

Handbook, pages 397–413. Cambridge University

Press.

Racer Systems GmbH Co. KG (2011). RacerPro, der OWL

Reasoner und Inference Server für das Semantic Web.

http://www.racer-systems.com/. Stand: 8. März 2012.

Randell, D. A., Cui, Z., and Cohn, A. G. (1992). A spa-

tial logic based on regions and connection. In PRO-

CEEDINGS 3RD INTERNATIONAL CONFERENCE

ON KNOWLEDGE REPRESENTATION AND REA-

SONING.

Renz, J. and Nebel, B. (2007). Qualitative spatial rea-

soning using constraint calculi. In Aiello, M., Pratt-

Hartmann, I., and van Benthem, J., editors, Handbook

of Spatial Logics, pages 161–215. Springer.

Skiadopoulos, S. and Koubarakis, M. (2004). Composing

cardinal direction relations. Artif. Intell., 152:143–

171.

Stocker, M. and Sirin, E. (2009). Pelletspatial: A hybrid

rcc-8 and rdf/owl reasoning and query engine.

Tsang, E. (1993). Foundations of Constraint Satisfaction.

Academic Press, London, San Diego, New York.

Vassiliadis, V. and Mungall, C. (2012). A toolbox

for Qualitative Spatial Reasoning in applications.

http://www.semanticweb.gr/thea/index.html. Date:

March, 10th 2012.

SupportingMobileRobot'sTasksthroughQualitativeSpatialReasoning

399