
Finite Belief Fusion Model for Hidden Source Behavior Change
Detection
Eugene Santos Jr.
1
, Qi Gu
1
, Eunice E. Santos
2
and John Korah
2
1
Thayer School of Engineering, Dartmouth College, Hanover, NH, U.S.A.
2
National Center for Border Security and Immigration, The University of Texas at El Paso, El Paso, TX, U.S.A.
Keywords: Belief Change, Behaviour Change, Finite Belief Fusion Model, Hidden Source Detection.
Abstract: A person’s beliefs and attitudes may change multiple times as they gain additional information/perceptions
from various external sources, which in turn, may affect their subsequent behavior. Such influential sources,
however, are often invisible to the public due to a variety of reasons – private communications, what one
randomly reads or hears, and implicit social hierarchies, to name a few. Many efforts have focused on
detecting distribution variations. However, the underlying reason for the variation has yet to be fully
studied. In this paper, we present a novel approach and algorithm to detect such hidden sources, as well as
capture and characterize the patterns of their impact with regards to the belief-changing trend. We formalize
this problem as a finite belief fusion model and solve it via an optimization method. Finally, we compare our
work with general mixture models, e.g. Gaussian Mixture Model. We present promising preliminary results
obtained from proof-of-concept experiments conducted on both synthetic data and a real-world scenario.
1 INTRODUCTION
A person’s beliefs and attitudes are key elements for
inferring the meaning of opinions held by
individuals and groups. These elements/perceptions,
however, are not stable and may change over time
through the processes of social interaction and first-
hand experiences (Hill and Kriesi, 2001). Studies on
social influence theories have shown that social
influence may have qualitatively different effects,
and that it may produce different kinds of change.
One simple case is how likely an individual will
adopt the attitudes and beliefs of other sources and
by how much. For example, in the context of
socialization of children, a child who has a strong
bond with his family is inclined to take parental
attitudes and actions with full trust. In contrast,
people only selectively accept the arguments and
views supported by online news sources, e.g.
consumer review sites. Opinions adopted with
different reliabilities will differ in terms of their
qualitative characteristics, and affect a person’s
subsequent behavior. Moreover, the patterns of
belief-changing behavior can be treated as an
indicator of different types of social influence
processes. For instance, in the process of self-
identification, the logic of how an individual
actually believes in the opinions does not depend on
observability of the influencing sources. It depends,
nevertheless, on his identity activated at that given
moment (Kelman, 1961). Thus, if we know the role
that social influence plays in behavior change at
each time period and the impact it has on a person’s
initial beliefs, we will be able to provide more
insights and explanations on the observed opinion
trend, and further, make predictions about other
likely behavioral consequences.
However, the characteristics of opinion sources
that affect people’s beliefs and attitudes are rarely
open to the public. Likewise, it is impossible to track
how people view and adopt the opinions held by
each of the sources they have interacted with. Such
information can be concealed subconsciously when
the influence is subtle or the reliability is not
quantifiable, whereas sometimes people will
intentionally conceal this information. For example,
terrorists tend to protect criminal organizations by
hiding their connections with the group. Therefore, it
becomes critical to develop a flexible model that can
1) support the social influence theory of
belief/opinion change; 2) detect and characterize the
hidden influential sources; and, 3) discover the
17
Santos Jr. E., Gu Q., E. Santos E. and Korah J..
Finite Belief Fusion Model for Hidden Source Behavior Change Detection.
DOI: 10.5220/0004130100170024
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2012), pages 17-24
ISBN: 978-989-8565-29-7
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

patterns/trend of the source’s impact on the observed
opinion change.
Bayesian approaches have been widely used to
represent belief and opinions (Garg et al., 2004,
Santos Jr. et al., 2011a). Among those, Bayesian
Networks (BNs) (Pearl, 1988) are a popular
probabilistic model due to its sound theoretical
foundations in probability theory combined with
efficient reasoning. For example, (Garg et al., 2004)
introduces a BN based divergence minimization
framework to integrate opinions from different
sources in order to solve the problem of standard
opinion pooling. However, people’s belief,
structured as a knowledge-based system, is
necessarily associated with some degree of
incompleteness, which turns out to be problematical
to BNs, as they require a completely specified
conditional probability table (CPT). BNs also
require that information be topologically ordered
which further restricts their general applicability to
real-world situations. In this work, we build our
model based on Bayesian Knowledge Bases (BKBs)
(Santos and Santos, 1999), as it has been extensively
used to model complex intent-driven scenarios
(Santos et al., 2011a; Santos et al., 2011b).
At each time period, the formation of individual
belief can be viewed as a process of aggregating
opinion/information from different sources. The goal
is to arrive at a single probability distribution that
represents the integrated knowledge base. Santos et
al. (2011c) proposed an algorithm to encode and
fuse a set of belief networks from different sources
into one unified BKB. Due to the nature of BKBs
and the mathematical foundations of fusion, we
derive a new modelling approach called a Finite
Belief Fusion Model (FFM) to capture the
characteristics of opinion-changing behavior. We
can then show how to detect underlying hidden
sources of change together with the corresponding
influential factors through a non-linear optimization
problem.
2 BELIEF FUSING MODEL
2.1 Related Work
Anomaly detection has been applied to detect the
presence of any observations or patterns that are
different from the normal behavior of the data (Das
et al., 2008). Works based on Bayesian Networks
include detecting anomalies in network intrusion
detection (García-Teodoro et al., 2009) and disease
outbreak detection (Wong et al., 2003). The typical
approach of BN-based anomaly detection is to
compute the likelihood of each record in the dataset
and report records with unusually low likelihoods as
potential anomalies. Different from these approaches
whose main goals are to achieve early detection and
identify anomalous change in terms of a probability
distribution (Das et al., 2008), we focus on detecting
the reasons behind the behavior change. Moreover,
many statistics-based anomaly detection methods
only focus on detecting events whose patterns are
anomalous enough to be distinguishable from
normal data. Furthermore, they overlook the
situation when certain external opinion sources that
have subtle influences at present, may cause a
butterfly effect later, as triggered by other events.
We show that our work overcomes the above
limitations by being able to detect less substantial
influencing sources.
There are some other techniques that attempt to
handle changing belief networks. Methods based on
learning Dynamic Bayesian Networks (DBNs)
(Dean and Kanazawa 1989) have provided
mechanisms for identifying conditional
dependencies in time-series data, such as for
reconstructing transcriptional regulatory networks
from gene expression data (Robinson and
Hartemink, 2010) and speech recognition using
HMM (Gale and Young, 2008). Nevertheless, most
DBN implementations assume for the sake of
efficiency that the Markov property holds for the
domain they represent, which restricts knowledge
engineering by requiring that the probability
distribution of variables at time depends solely on
the single snapshot at time 1. Thus, for real
world cases when the future outcomes are highly
dependent on the hidden factors whose prior
information is unidentified, we need another model
that can easily express such abstract temporal
relationships.
For each of the opinion sources, we would
expect the probability of generating a series of
responses follows a particular type of pattern.
Similarly, the reliability of an opinion is also likely
to vary across sources. This results in a natural
expectation that we need a model that is capable of
mixing belief networks from different sources
together. Hill and Kriesi (2001) apply a Finite
Mixture Model to support their theory of opinion-
changing behavior, where the attitude of each of the
group is represented by a distribution and the mixed
distribution is described by a weighted aggregation
of different distributions. However, the
Expectation-maximization (EM) based mixture
decomposition methods show propensity to identify
KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
18
local optima (McLaughlan and Peel, 2000), which
makes it also sensitive to initial guesses. In addition,
the separation of parameter estimation and
component identification increases the probability of
converging to boundary values when the number of
model components exceeds the true one (Figueiredo
and Jain, 2002). These considerations led us to
develop a variant mixture model that is suitable for
our problem of detecting hidden belief sources by
taking advantage of time-varying information, as
well as loosening the requirement of a predefined
number of sources.
2.2 BKB
In this work, we assume that both of the initial
beliefs and hidden influencing sources at each time
period are represented by BKBs. BKBs are a rule-
based probabilistic model that represents possible
world states and their (causal) relationships using a
directed graph. BKBs subsume BNs by specifying
dependence at the instantiation level (versus BNs
that specify only at the random variable level); by
allowing for cycles between variables; and, by
loosening the requirements for specifying complete
probability distribution. BKBs collect the
conditional probability rules (CPR) in an “if-then”
style. Each instantiation of a random variable is
represented by an I-node and the rule specifying the
conditional probability of an I-node is encoded in an
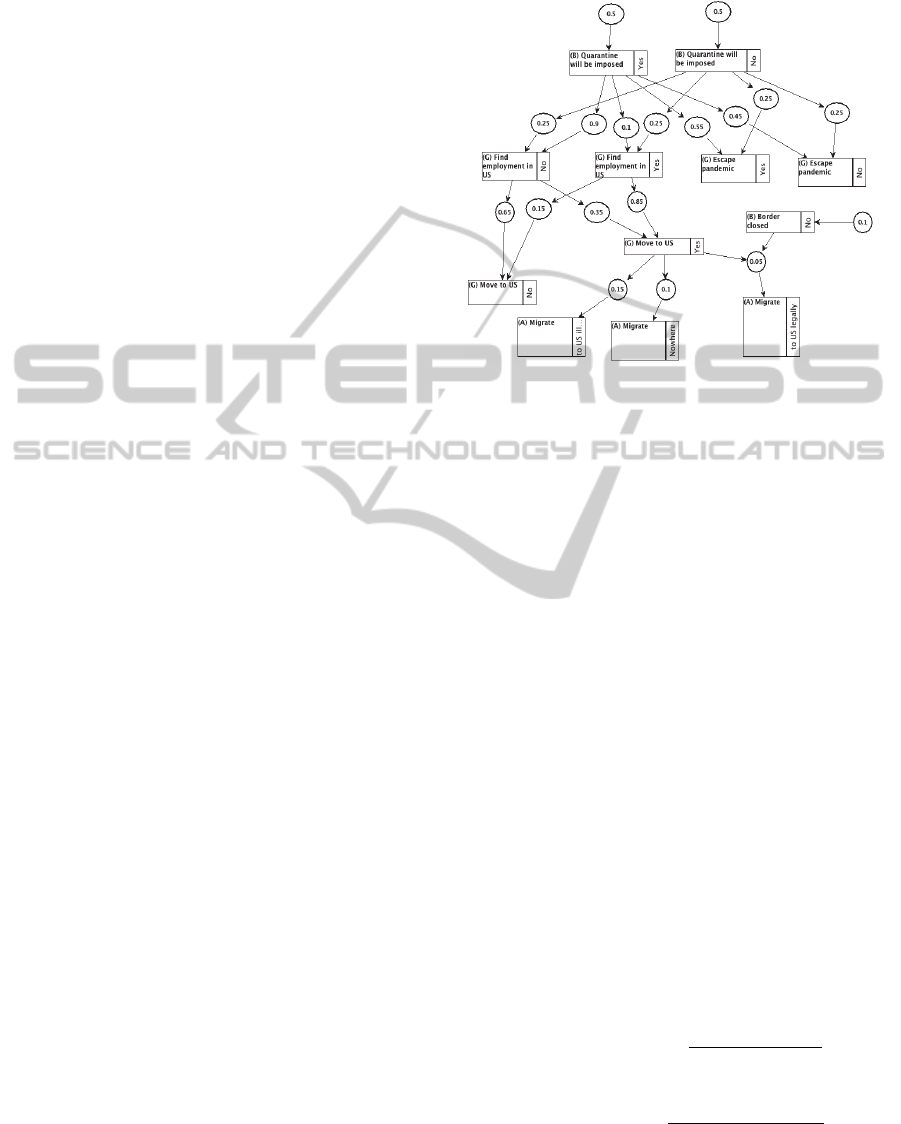
S-node with a certain weight/probability. Fig. 1
presents an example BKB fragment, with square
blocks and circles representing I-nodes and S-nodes,
respectively. Multiple fragments can be combined
into a single BKB using the Bayesian fusion
algorithm (Santos et al., 2011c). The idea behind this
algorithm is to take the union of all input fragments
by incorporating source nodes, indicating the source
and reliability of the fragments. Reasoning
algorithms are used in BKBs to make predictions
and provide explanations (Santos and Santos, 1999).
2.3 Building a Model
Our goal is to detect hidden opinion sources and the
corresponding impact patterns that result in behavior
change over time. However, without a sound
theoretical foundation, the methods developed will
simply be ad hoc. Social influence theories show
how the way people adopt beliefs and attitudes from
other sources varies across conditions/situations.
Sometimes, a person will not accept these external
ideas in total but only adopts the pieces that fit into
his own situation (Kelman, 1961). Therefore, we
develop a model that is specifically tailored to take
into account of all these points.
Figure 1: Sample BKB fragment from an intent
framework.
2.3.1 Finite Belief Fusion Model (FFM)
We develop a finite belief fusion model to represent
a person’s actual belief distribution. Formally, a
finite belief fusion model is defined as
p'(x) fuse(w
0
, p,
w,
h)
w
i
1
i0
where and
denote the initial belief distribution
and initial reliability, respectively.
,
,…,
represents how a person views and
trusts the opinion sources
,
,…,
, where
both
and
are implicit to the observer. Instead of
simply adding up the weighted input distributions
linearly like general mixture model, the new belief
distribution ′ is generated through the BKB fusion
algorithm. An important property of the fusion
algorithm is the capability to support transparency in
analysis. In other word, all perspectives are
preserved in the fused BKB without loss of
information. Since the fused belief is still a valid
BKB, for each of the random variable in ′, let
be the parent variables of . We have
p'(v x | v
pa
y)
p'(v x, v
pa
y)
p'(v
pa
y)
x
x
p'(v x, v
pa
y)
x
p'(v
pa
y)
1
where
FiniteBeliefFusionModelforHiddenSourceBehaviorChangeDetection
19

p'(v x, v
pa
y) w
0
p(v x, v
pa
y)
w
i
h(v x, v
pa
y)
i1
p'(v
pa
y) w
0
p(v
pa
y) w
i
i1
h(v
pa
y)
Social influence theory suggests that people’s beliefs
are partially affected by the external sources. In this
work, we consider a simplified situation when each
of the hidden sources only affects one part of the
initial belief , such that the conditional probability
distribution of a particular variable will not be
changed by more than one source. This could
happen when people prefer to take the attitude from
the source whose belief/opinion is most convincing
in a particular field of knowledge. Then, the above
model can be simplified as:
'( , ) ( , )
(1 ) ( , )
'( ) ( ) (1 ) ( )
'( , ) '( )
pa pa
pa
pa pa pa
pa pa
x
p v xv y whv xv y
wpv xv y
p
vywhvy wpvy
pv xv y pv y
(1)
where is the only influencing source that affects .
2.3.2 Detection Algorithm
Now, we generalize the problem by considering a
series of beliefs: given belief trend
,
,
,…,
generated over t time periods, the goal is to learn the
probability distribution for each of the potential
hidden BKBs
( 1:), as well as its time
varying impact
1: . Considering that the
causal relationship in human belief systems is less
likely to change, we assume that all belief networks
share the same (causal) structure, but vary on
probability distribution. Note,
0 if source
has no impact at time .
Let
be the variable influenced by source
and let and denote two states representing
and
,
, we rewrite (1) as:
0
0
() () (1 ) ()
() () (1 ) ()
() ()
jiji ij
jiji ij
jj
pwh wp
pwh wp
pp
(2)
where
,
and
are unknown parameters
needed to be learned from the given belief trend.
Let
,
,…,
be the impact series
of source
, we learn
,
and
via the
following constrained optimization problem
(, ) (, )
** *
1
,,
[(),(), ]argmin ( )
jij jij
i
t
fw fw
ii i
j
w
hhw e e
s.t.
∀,
∑
0, 1:
where
,
1
We apply Sequential Quadratic Programming (SQP)
algorithm (Nocedal and Wright, 2006) to do the
optimization, as the linear algebra routines it uses
are more efficient in both memory usage and speed
than the active-set routines.
So far, we have addressed the problem of
characterizing the hidden source
and its impact
pattern with respect to variable
. We apply the
algorithm to all variables ( 1:) and get
impact trends.
Considering that some hidden sources may affect
a fragment of initial belief that contains more than
one variable, it is reasonable to believe that the
variables that generate similar impact trends are
affected by the same hidden source and should be
represented in one distribution. We treat the weight
at each time step as a feature and apply clustering
algorithms (Xu and Wunsch, 2005) such as K-means
to detect similar trends. The optimal number of
hidden sources is achieved when the sum of inter-
class variance is less than a threshold.
3 EXPERIMENTS
In what follows, we present results of experiments
that were carried out on both simulated data and a
real world scenario. We studied the performance
characteristics of our algorithm in simulation studies
that vary by several orders of magnitude in the
number of variables, number of hidden sources and
number of time steps.
3.1 Simulated Data Set
To evaluate the effectiveness of our method, we
simulate a person’s actual belief trend from his
initial belief and some hidden external sources,
where the external sources are unknown to the
detection model. We start with a small dataset, in
which both of the initial belief and hidden sources
are represented by a simulated five variables BKB
(same structure, different distribution). In this
experiment, we select only one hidden source. Then
for every time period, we sample 1000 records from
initial belief and hidden source respectively. The
testing data is generated by mixing samples from
two different distributions together with a randomly
assigned hidden weight ranging from 0 to 1.
KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
20

Figure 2: Comparison of detected weight for FFM (blue line) and GMM (green line) methods with different number of time
steps. The red line with diamond mark is the real weight trend.
In order to examine how the amount of time-
varying data affects our detection performance, we
choose three different numbers of time steps: 10, 50
and 100. The conditional probability parameters of
the belief network at each time step are learned from
the testing data using smoothed maximum likelihood
estimation (Das et al., 2008). To compare with the
state-of-art mixture models, we run the same testing
data on Gaussian Mixture models (GMMs), one of
the most statistically mature methods for mixture
model clustering. The weight of each component is
learned through mixture decomposition. Figure 2
plots the impact trend detected using FFM and
GMM respectively in terms of number of time steps,
from which we can see that the hidden impact
pattern we captured is pretty consistent with the true
trend. Also, when the hidden impact values are very
small, our detection results are still accurate. This
fact enables us to detect less substantial influencing
sources. The mean and standard deviation of the
detection errors (difference between true and learned
weight) can be found in Table 1a. In contrast to
GMM, our method shows a higher accuracy with a
smaller variance. Additionally, we see that the
average accuracy of FFM increases with the number
time steps, which indicates that our method is
capable of improving detection performance by
leveraging time-varying knowledge. Moreover, we
compare the distribution of a hidden source learned
during the detection process with the true one. Chan
and Darviche (2002) proposed a distance measure
between two probability distributions, where the
distance is defined as:
D(P, P') ln max
w
P'(w)
P(w)
lnmin
w
P'(w)
P(w)
We apply this metric in our evaluation due to its
ability to bound belief changes comparable to KL-
divergence. The results provided in Table 1b suggest
that the distribution of the hidden source we learned
is closer to the real distribution than GMM.
Table 1a: Mean and Std of the detection errors.
Detection Error 10 steps 50 steps 100 steps
FFM (Mean) 0.0385 0.0281 0.0253
GMM (Mean) 0.3123 0.2219 0.2361
FFM (std) 0.0263 0.0160 0.0166
GMM (std) 0.1248 0.1386 0.1361
Table 1b: Distance measure between the true and learned
probability distribution using different algorithm.
Distance 10 steps 50 steps 100 steps
FFM 0.5618 0.5137 0.4742
GMM 2.3145 1.9723 2.1687
To evaluate the scalability of our technique, we
also simulate data from a 30 variables network with
100,000 mixture records generated at each time step.
We ran our experiment on nine different hidden
sources and present the results in Figure 3.
Apparently, our method scales well to large network.
Next, we conduct a more detailed analysis of
performance by looking at detection results on each
run. The largest error comes from the sixth trial. We
examine the hidden sources involved in this trial and
find that the distribution of the hidden source is very
similar to the initial belief. Thus, it becomes more
difficult to accurately detect the hidden impact, as
the varied belief at each time step is insensitive to
the value of impact.
Finally, we examine the ability of our method to
detect multiple hidden sources. We choose n hidden
1 2 3 4 5 6 7 8 9 10
0
0.5
1
time step
hidden Weight
true trend
FFM
GMM
0 5 10 15 20 25 30 35 40 45 50
0
0.5
1
time step
hidden Weight
0 10 20 30 40 50 60 70 80 90 100
0
0.5
1
time step
hidden Weight
FiniteBeliefFusionModelforHiddenSourceBehaviorChangeDetection
21
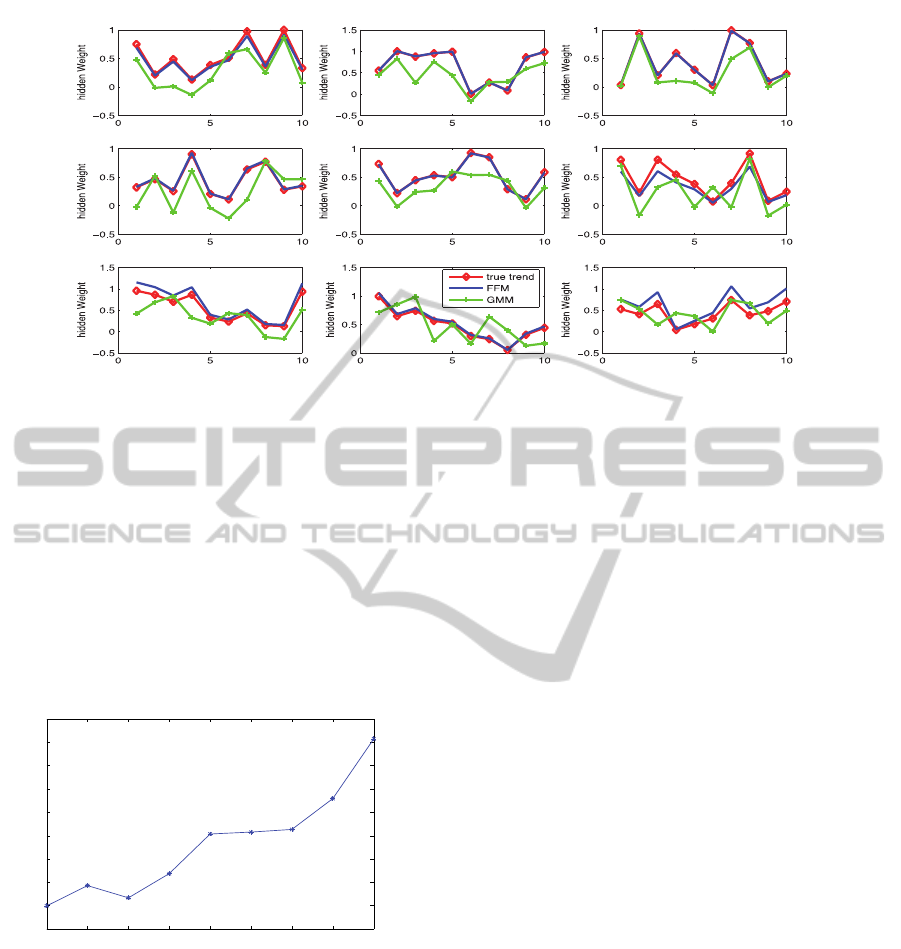
Figure 3: Comparison of detection results on large dataset.
sources ( 1: 9), where each of them affects one
fragment of the initial network with a certain weight.
We follow the same procedure as the second
experiment except that the mixture records are
generated from n different hidden sources. Figure 4
depicts the average detection error with respect to
the number of hidden sources. As we can see, the
error grows with the number of sources. This is due
to the increased degree of freedom brought about by
multiple fragments fusion as it enlarges the potential
solution space. Nevertheless, the largest error is still
less than 0.1.
Figure 4: Average detection error in terms of the number
of hidden sources.
3.2 H1N1
In this subsection, we apply our method to identify
the impact patterns behind the events that happened
during the H1N1 pandemic in Mexico. Santos et al.
(2011a) conducted a Cross-Border Epidemic Spread
project to study why and under what circumstances
would people be driven to cross the border both
legally and illegally with respect to epidemic spread.
In order to understand such human behavior as well
as the intent, they employed the intent framework
represented by BKBs to model people’s reaction to
the various events that took place during the
pandemic in 2009. The whole intent system is
constructed through the fusion of cultural BKB
fragments that are created based on sources such as
demographic information and news articles. When a
major event occurs, the intent system will update its
probability distribution adaptively to reflect an
individual/group’s belief change caused by the
event. Therefore, the characteristics of these events
and their impact patterns are key to analysing
people’s reactions. We apply our method on a series
of intent systems modelled in the paper (Santos et
al., 2011a) to detect the implicit events without any
foreknowledge. Figure 5 displays our detection
results, where two potential/unknown events,
represented by blue and red dotted lines are
successfully detected.
To figure out what these two events could be, we
plot the probability of “people believe disease is
contagious” over time in Figure 5. As we can see,
the probability achieves its peak on May-1-09 and
starts to decline on Jul-15-09, which shows a strong
correlation with the impact pattern from the second
event. This finding indicates that the breakout of the
second event causes a temporary increase on
people’s belief regarding the contagious nature of
the disease. In comparison, the event that happened
on Apr-24-09 had no direct impact on such belief
change. In fact, according to the timeline of H1N1,
we find that two events: “WHO sends experts to
Mexico” on Apr-24-09 and “Government published
an announcement to advise people staying at home”
on May-1-09 match perfectly with our detection
result. The learned distribution of the WHO event
suggests an increase in the probability of “believe
healthcare is effective” by 0.225. However, there is
1 2 3 4 5 6 7 8 9
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
number of hidden sources
average detection error
KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
22
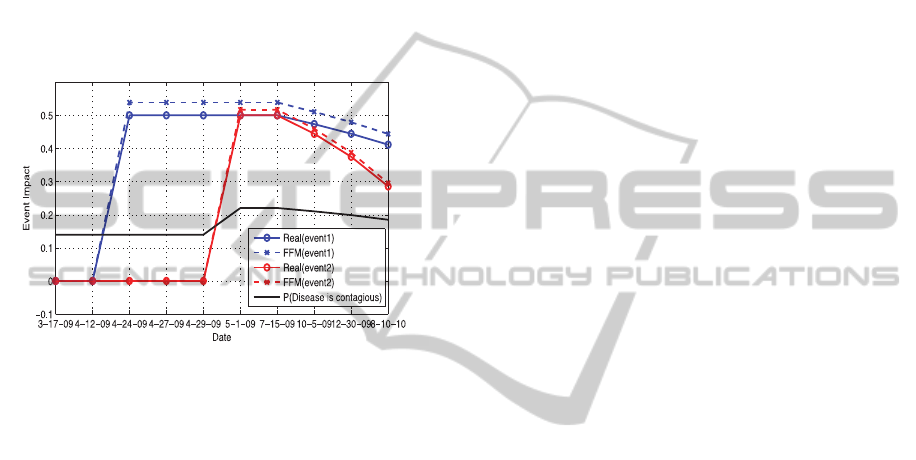
no direct causal relationship between the
effectiveness of healthcare and the contagiousness of
H1N1, so the impact from the “WHO” will not be
reflected by how people think of the disease. This
explains why people did not change their beliefs
about the contagiousness of H1N1 until they
received the government’s announcement, even
though the WHO was already sending in experts
since April. Moreover, we compare the impact
patterns we detected with the true trend. As shown
in Figure 5, our results are very close to the
modelled scenario (solid lines), which helps point
towards the effectiveness of our approach.
Figure 5: Detection results on event impact. Two events
represented by blue and red lines are detected. The black
solid line indicates the probability of “people believe
disease is contagious”.
4 CONCLUSIONS
In this paper, we presented a new approach to detect
hidden sources of influence, as well as capture and
characterize the patterns of their impact with regards
to belief-changing trends. We formalize the problem
as a finite belief fusion model and solve it via an
optimization method. We demonstrate that FFM
outperforms the classic Gaussian Mixture Models in
both small and large synthetic datasets. In addition,
we applied our method to identify implicit events
that happened during the H1N1 pandemic in
Mexico. Also, the detection results generated by
FFM were consistent with the modelled scenario.
In future work, we will expand our approach by
allowing multiple sources to affect the same part of
the belief network. This happens when there is no
convincing source for a particular fragment and the
final knowledge/belief system is formed by
integrating all possible explanations.
ACKNOWLEDGEMENTS
This work was supported in part by AFOSR, DHS,
and ONR.
REFERENCES
Hill, J. L. and Kriesi, H, 2001, An Extension and Test of
Converse's "Black-and-White" Model of Response
Stability. The American Political Science Review, Vol.
95, No. 2, pp. 397-413
Kelman, HC. 1961. Processes of opinion change. Public
Opinion Quarterly. 25:57-78
Garg, A., Jayram T. S., Vaithyanathan. S, Zhu, H, 2004.
Generalized Opinion Pooling. In Proceedings of the
8th Intl. Symp. on Artificial Intelligence and
Mathematics.
Pearl, J. 1988. Probabilistic Reasoning in Intelligent
Systems: Networks of Plausible Inference.
Santos, Jr., E., and Santos, E. S. 1999. A framework for
building knowledge-bases under uncertainty. Journal.
of Experimental and Theoretical Artificial Intelligence
11(2):265–286.
Santos, Jr. E., Wilkinson, J. T, and Santos, E. E, 2011c,
Fusing multiple Bayesian knowledge sources.
International Journal of Approximate Reasoning,
Volume 52, Issue 7, pp 935-947
Das, K., Schneider, J., and Neill, D.B. 2008. Anomaly
pattern detection in categorical datasets. Proceeding of
the SIGKDD Conf. on Knowledge Discovery and Data
Mining, pp 169-176.
García-Teodoro. P, Díaz-Verdejo. J, Maciá-Fernández. G,
Vázquez. E. 2009. Anomaly-based network intrusion
detection: Techniques, systems and challenges.
Computers Security, Volume 28, Issues 1–2, pp18-28
Wong, W., Moore, A., Cooper G. and Wagner, M. 2003.
Bayesian Network Anomaly Pattern Detection for
Disease Outbreaks. Proceedings of the 20th ICML
Dean, T. and Kanazawa, K. 1989. A model for reasoning
about persistence and causation, Artificial Intelligence
93(1–2): 1–27
McLachlan G and Peel, D. А. 2000: Finite mixture
models. New York: Wiley
Figueiredo, M. A. T. and Jain, A. K. 2002. Unsupervised
learning of finite mixture models. IEEE Transactions
on Pattern Analysis and Machine Intelligence 24(3):
381–396
Gales, M. and Young, S. 2008. The Application of Hidden
Markov Models in Speech Recognition, Foundations
and Trends in Signal Processing: Vol. 1: No 3, pp
195-304
Robinson, J. W. and Hartemink, A. J. 2010. Learning
Non-Stationary Dynamic Bayesian Networks. Journal
of Machine Learning. Res. 9999. pp 3647-3680.
Xu, R. and Wunsch, D. 2005. Survey of clustering
algorithm. IEEE Transactions on Neural Networks,
Vol. 16, No. 3, 645-678
FiniteBeliefFusionModelforHiddenSourceBehaviorChangeDetection
23

Chan, H and Darwiche, A. 2002. A distance measure for
bounding probabilistic belief change. In Proceedings
AAAI, pages 539– 545
Santos, E. E.; Santos, E..; Korah, J.; Thompson, J.E.;
Keumjoo Kim; George, R.; Gu, Q; Jurmain, J.;
Subramanian, S.; Wilkinson, J.T., 2011a, Intent-
Driven Behavioral Modeling during Cross-Border
Epidemics, SocialCom, pp.748-755K.
Santos, Eunice, E., Santos, Eugene, Jr., Wilkinson, John
T., Korah, John, Kim, Keumjoo, Li, Deqing, and Yu,
Fei, Modeling Complex Social Scenarios using
Culturally Infused Social Networks, 2011b,
Proceedings of the IEEE International Conference on
Systems, Man, and Cybernetics, 3009-3016,
Anchorage, AK.
Nocedal, J. and S. J. Wright. Numerical Optimization,
2006, Springer Series in Operations Research,
Springer Verlag. Second Edition.
KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
24
