Creating an Educational Roadmap for Engineering Students via

an Optimal and Iterative Yearly Regression Tree using Data Mining

Marie Khair, Chady El Moucary and Walid Zakhem

Notre Dame University – Louaize, North Lebanon Campus, Barsa, El Koura, Lebanon

Keywords: Educational Data Mining, Cart, Optimal Regression Tree, Courses Roadmap, GPA, Engineering Schools,

Splitting Criteria, Pruning Levels, Precision.

Abstract: Targeting high academic standards is required in engineering studies. Advisors usually play an important

role in helping students keeping good records and transcripts along their educational path by helping them

choose their courses and keeping track of their grades. However, performance in some courses in the

curriculum embodies determining repercussions and might inadvertently jeopardize the overall students’

Grade Point Average (GPA) in an irreversible manner. The purpose of this paper is to draw an educational

roadmap that helps advisors and students being aware of the turning points that decisively affect their

overall cumulative GPA and act upon a current outcome. This roadmap is based on Classification and

Regression Trees where nodes and branches denote the aforementioned courses and students’ performance,

respectively, with the ultimate outcome being the overall student’s GPA upon graduation. The tree is

constructed based on a relatively large number of records with 10-fold cross-validation and testing.

Moreover, the tree is produced on a yearly basis with a twofold objective. The first is to secure a high level

of precision by applying it over a short period of time and the second is to allow for injecting each-year

computed GPA with the remaining courses as to reflect the actual situation with maximum vraisemblance.

This iterative and recursive tree achieves a very close tracking of students’ performance and provide a

powerful tool to rectify courses’ track and grades for each student individually while aiming at a predefined

final GPA. Furthermore, the choice of the optimal tree was carefully examined in the light of the relatively

elevated number of attributes. In this context, diverse models were created and performance and/or

precision were computed in terms of different values of “pruning levels” and “splitting criteria”. The choice

of the best tree to be adopted for advising is thoroughly explained. Besides, it is shown, in this context, that

the structure of the tree remains highly versatile in the sense that it can be revisited at any point for further

assessment, adjustment, and expansion. Finally, yet importantly, simulation results were carried out using

Matlab CART and demonstrated high efficiency and reasonably precise results.

1 INTRODUCTION

In the last decades, data mining has become an

indispensable tool in dealing not only with large

databases; it has been adopted as a solution for

drawing pertinent information and extracting hidden

knowledge in cases where the number of attributes is

relatively comparable to the number of records as

well (Kovačić and Green, 2010), (Fayyad et al.,

1996), (Piatetsky-Shapiro, 1991), (Baker and Yacef,

2009). It is known that patterns can be drafted easier

when the number of samples is significantly large

but at the cost of computational requirements and

sophisticated data mining techniques (Thabtah,

2006). Nonetheless, it has been validated that

exercising data mining in some fields does not

require excessive amounts of data at the condition

that the data miner demonstrates an advanced level

of understanding of the figures he possesses.

Data mining finds innumerable applications in

almost all sectors and aspects of our society.

Amongst others, data mining is being extensively

such as medicine, forensics, banking, jurisdiction,

landscaping, astronomy, etc., notably when ad hoc

situations arise and when previous and lucid

practices have not yet been ruled (Silverstein et al.,

2000). Recently, Data Mining has being

interchangeably used with what it is referred to as

Knowledge Discovery in Databases or KDD

(Fayyad et al., 1996).

One interesting application of data mining is the

Khair M., El Moucary C. and Zakhem W..

Creating an Educational Roadmap for Engineering Students via an Optimal and Iterative Yearly Regression Tree using Data Mining.

DOI: 10.5220/0004130300430052

In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2012), pages 43-52

ISBN: 978-989-8565-30-3

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

field of Education. Indeed and in the last few years,

data mining has been adopted and validated as one

of the primary and foremost scientific methods used

in approaching different operational perspectives in

Colleges and Higher-Education Institution.

Furthermore, a standalone field of data mining has

emerged and is referred to as Educational Data

Mining or EDM (Sembiring et al., 2011), (Wook,

Yahaya et al., 2009), (Chadha and Kumar, 2011),

(Domingos, 2007), (hxxp://www.educationaldatami

ning.org), (Baker and Yacef, 2009). As a matter of

fact, Education has grown to such an extent where it

does not simply embrace teaching and education per

se, but it became a full-fledged business with

numerous departments requiring experts and

professionals from different disciplines to efficiently

support its operation. Additionally, data and

information that are being treated and/or processed

on daily, semestrial, and yearly basis, have

drastically increased to a point where traditional

methods and practices no more suffice. Academic

performance, students’ attrition, course offerings,

grant management, students’ behavior, etc. are

amongst many other issues and influential

parameters that necessitate innovative and potent

techniques for analysis and solutions (Al-Radaideh

et al., 2006), (Kovačić, 2010), (Portnoi et al.2011),

(Eshghi et al., 2011), (Al-Radaideh et al., 2011),

(Dekker et al., 2009), (Bardawaj and Pal, 2011).

Finally, dealing with the growth in the number of

students and the ever-changing teaching

methodologies dictate new prescription with solid

ground.

In this paper we will elaborately visit this side of

EDM by drafting an educational roadmap for both

students and advisors to help sustaining elevated

rates of success and more precisely target a desired

GPA upon graduation for engineering schools and

universities. The customary practice dictates that

academicians help their students keeping acceptable

performance by advising them during registration, in

the light of their previous achievements, on the type

and number of courses they need to enroll in (Portno

et al., 2011), (Oladokun et al., 2008), (Pal and

Baradwaj, 2011). However, performance in some

key courses proved to have irreversible

repercussions on students’ overall GPA. These

courses can be directly and/or indirectly prerequisite

for more advanced courses’ materials or refer to

some Physics and/or Math courses, or even language

courses, namely when studies are in a foreign

language. The situation relies on schools’ individual

programs and courses’ structure and thus, might

significantly vary. Consequently, advisors and

students might be misled in many cases at the

critical point of registration especially when students

advance along their curricula and the tree becomes

more complicated thus, involving more parameters

to embrace for an appropriate decision.

The purpose of the educational roadmap is to

draft a yearly decision tree that lucidly underlines

the courses that students should pay special attention

to in order to sustain a good performance.

Furthermore, the tree not only cites the courses but it

clearly indicates the grades that students’ have to

earn in order to attain their final GPA upon

graduation. In this sense, the roadmap creates a

scientific and computational direct link between the

outlines courses and a “targeted” performance for

engineering students upon graduation. The tree is

created for every year as to keep the closest possible

tracking system and the most likelihood that reflects

the actual students’ performance as well.

Additionally, two types of trees can and will be

elaborated with two different approaches. In the first

type, the tree exclusively includes the courses taken

during the current year of studies with the purpose of

emphasizing on the most important courses and their

respective grades for the targeted performance, for

that specific year. The second type of tree is

somehow recursive and individual since the

cumulative GPA of the previous year(s) will be

injected in the attributes as to indubitably reflect the

path of a given student and identify his/her current

situation and thus, derive pertinent decisions. The

roadmap is built using Data Mining Regression

Trees with a 10-fold cross validation. In this sense,

trees will be trained, validated then tested for their

efficiency.

This paper will be divided into five parts. After

the introduction, section II presents a quick

overview of data mining algorithms, approaches and

applications. In the third section, data is presented

and analysed. The innovative approach is

comprehensively outlined and explained as well.

Simulation results are shown in the frame of the

application and elaborate analysis is detailed to

demonstrate the effectiveness of the approach.

Additionally, section III includes a user manual for

the suggested educational roadmap. In section IV,

future scope of this study will be shortly presented.

Finally, conclusions and perspectives for future

work are drawn in section 5.

2 DATA MINING

There exist many definitions for data mining in

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

books and research papers (Witten et al., 2011),

(Han et al., 2011). They all refer to data mining as

an interdisciplinary field in computer science which

achieves interactive and iterative processes aiming at

unveiling hidden, but existing, patterns and/or

relationships amidst data using statistical and

mathematical procedures with a prime objective of

providing decision support systems with information

and knowledge. Generally, data mining can be

referred to for two different objectives. The first is

predicting future values of some variables of interest

based on a recorded database of evidences. The

second, referred to as description, focuses on finding

hidden patterns relating data features. The latter

exercise finds its application in Knowledge-

Discovery-in-Database (KDD) cases where the

former one is an objective in machine learning

applications.

2.1 CART for Data Mining

Exercising data mining requires primary steps for a

reliable outcome. The collected data is to be

subdivided for training, testing, and validation. In

our case, we used 70% of the data for training, 15%

for cross-validation and 15% for testing. During the

training stage, a temporary model is engendered and

which simulates rudimentary relationships between

the attributes and the targeted output. An important

stage follows and which is referred to as validation.

This stage reveals crucial and decisive namely when

the number of attributes is relatively elevated

compared with that of the samples. The outcome

will be a general enhancement of the model’s

accuracy where over-fitting occurrences are reduced

and non-existing patterns are avoided. Additionally,

typical glitches could be circumvented such as

undesirable memory characteristic that results in a

false generalization. For instance, assume that in the

selected data for training, all students who have

passed a certain course have obtained a GPA beyond

a certain value; we do not want the model to

remember or create this relationship (Silverstein et

al., 2000). Furthermore, an overall performance key

is the pruning level or more precisely the splitting

value. It is a number “n” such that impure nodes

must have “n” or more observations to be split.

Besides, during the cross-validation stage, the cost

of the tree is the sum over all terminal nodes of the

estimated probability of that node times the node's

cost. If “t” is a regression tree, the cost of a node is

the average squared error over the observations in

that node. The cost is a vector of cost values for each

subtree in the optimal pruning sequence for “t”. The

resubstitution cost is based on the same sample that

was used to create the original tree, so it

underestimates the likely cost of applying the tree to

new data (Thabtah, 2006). Once validation is

performed, testing is used to evaluate the validated

model. In this stage, new or untrained data is applied

with the purpose of gauging the model. Here the

expertise of the data miner plays a key role; miners

should use their savvy to assess the performance and

accuracy of the model. In some cases, using

different algorithms or revisiting the entire

procedure might reveal necessary. Finally, when the

model is satisfactory, the data miner shall transform

the outcome into information and knowledge to be

adopted for future decision-making and analysis.

2.2 Data Mining Tasks

Data mining objectives can be carried out by means

of various procedures, frequently called tasks (Wu

and Kumar, 2009). Thus a further categorization of

data mining is obtained:

Classification: The most frequently used

classifiers are Decision Trees, Bayesian and Neural

Networks, etc. and which are widely used in

Handwriting and Speech Recognition, Web Search

Engines, etc. (Quinlan, 1986).

Regression: This task aims at

forecasting/calculating the probability or the value

of a variable via an iterative minimization of some

error functions. Classification And Regression Trees

(CART) are primary procedures for this task. It is

referred to as classification or regression if the

variable to be forecasted is nominal (belongs to a

certain defined set) or continuous (assumes infinite

number of values), respectively (Quinlan, 1986).

Clustering: K-Means and Fuzzy Clustering are

well-known techniques used for this purpose with

applications found in typical unsupervised learning

cases such as in Image Analysis, Biology and

Medicine, Education, etc. (Nock and Nielsen, 2006)

Association Rule Learning or Dependency

Modelling: The “Apriori” algorithm is the most

famous procedure used to identify frequent itemsets

in a database and deriving association rules. It is

mainly used in applications involving decisions

about marketing activities such as in supermarkets as

well as in the fields of Web Mining, Bioinformatics,

etc. (Agrawal et al., 1993), (Piatetsky-Shapiro, 1991)

Deviation/Outlier Detection: This is exercised in

applications such as Data Security for Fraud and

Intrusion Detection. (Denning and Dorothy, 1986).

Link Analysis: This task is practiced when

traditional approaches reveal inefficient (Getoor,

CreatinganEducationalRoadmapforEngineeringStudentsviaanOptimalandIterativeYearlyRegressionTreeusingData

Mining

2003).

3 PROBLEM STATEMENT AND

EDUCATIONAL ROADMAP

As previously mentioned, targeting high academic

standards is required in engineering studies. This

requirement not only reveals necessary throughout

the curriculum but is a prerequisite to entering a

highly competitive job market. Moreover, if the

engineering curriculum involves a BS followed by a

Master degree, this requirement becomes a turning

point in a student’s academic path. Acquiring certain

grades in major and technical courses is also a

primary goal for those students and is, in most cases,

a necessary condition for graduation. As it is known,

advisors usually play an important role in helping

their students sustaining good transcripts along their

studies; they are responsible for helping them choose

their courses based on their performance in order to

avoid situations such as falling under probation or

suspension. Nonetheless, and due to the fact that

engineering curricula involves courses from

diversified disciplines, the situation becomes

intriguing and complex. More specifically,

identifying courses that are a key for success might

reveal cumbersome.

Furthermore, a vital educational aspect that

haunts the mind of colleges’ and higher-education

institutions’ academicians is the performance of

their students throughout their academic path.

Curricula have become diversified involving

numerous courses from different disciplines that

sometimes leave students and academicians not

incapable of identifying the turning points and key

courses in dealing with some situations such as

avoiding probation, suspension, or more precisely

target a desired cumulative GPA) upon graduation.

This situation becomes more critical when dealing

with certain majors such as engineering (Oladokun

et al., 2008), (Kabra and Bichkar, 2011). Indeed,

when pursuing either a five-year Bachelor-of-

Engineering program or a three-year Bachelor-of-

Science followed by a two-year Masters-of-Science

or Engineering program, high academic standards

become a must notably at early stages of studies. It

is known that students’ transcripts should

demonstrate acceptable performance in major and

technical courses and a certain GPA is required for

graduation. The merciless competition in the job

market as well as in the Higher Education sector

only adds another burden on the advisors’ shoulders

making students’ performance a vital and decisive

attribute in the final outcome and eligibility.

Additionally, different values of splitting will be

comprehensively studied with the objective of

choosing the optimal tree for each year. The splitting

value in regression trees is a determining factor in

the estimation process’ precision and efficiency.

Additionally, correlation between the actual and

estimated values of students’ GPA will be studied as

to endorse and validate this choice. The correlation

analysis will be conducted exclusively on the testing

data without involving any trained records as to

undoubtedly yield a truthful and reliable choice. The

study conducted in this paper involves a little over

one thousand samples that were scrupulously

analysed, screened and pre-processed before

application to the data mining process. Three

hundred five samples were retained (Silverstein et

al., 2000). Simulation results demonstrated a highly

efficient outcome namely in terms of the testing

phase.

The objective of our research is to provide both

students and advisors a tool that we will call

educational roadmap with the primary goal of

keeping an accurate track of their academic route.

This roadmap is based on regression trees generated

on a yearly basis and which offer a straightforward

tool for follow up regarding each individual student

in choosing a well-defined academic performance

upon graduation. More precisely, the inputs to the

tree are the grades obtained in selected courses and

the output is the estimated final cumulative GPA.

The estimated GPA is not only an output but is a

choice determined by students upon enrolling in

engineering majors. In this sense, this approach is

innovative since it does not merely estimate the

GPA based on students’ grades in early stages but it

is rather a bottom-up approach. Students start from

the bottom of the tree and draw their path upward

while identifying the criteria that should be met for

their choice. The aforesaid key courses are

determined using regression analysis performed on a

relatively large number of engineering students’

records. According to the tree, students and advisors

can identify the weaknesses and/or strengths that

hinder and/or foster their choice. Moreover, the

generated trees offer the possibility to revisit the

grades of students in each of these courses on a

yearly basis and thus, allow them to rectify their

path by not only repeating those courses, but in

determining the minimum grade they should obtain

as well.

Two types of trees are produced on a yearly

basis. The first type aims at pinpointing the most

important courses whose weights contribute the

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

most towards the desired GPA and irreversibly

affect their path. The second type is based on

iterative trees created with students’ previous GPA

injected in the inputs. In this sense, a student’s

current GPA becomes one of the attributes in the

dataset during training, validation and testing. This

type of feedback allows for a more precise

projection of the real status of each student and

significantly augments the precision of the final

outcome.

3.1 Data Presentation and

Pre-processing

Data was gathered from 1100 students already

graduated from the Electrical and Computer and

Communication Engineering. Should a course be

repeated, the latter grade would replace the previous

one. A course can be repeated voluntarily should a

student require or be required to raise his GPA, these

students were excluded from this study as their final

grade point average was increased voluntarily

Several screening and pre-processing stages have

been applied to cleanse the data and eliminate

extreme cases which present misleading

relationships. Finally, three hundred five records

have been retained and which represent random

situations with diversified cases embracing the most

frequently encountered in a student’s life. The table

below summarizes the samples recorded with

regards to their performance.

Table 1: Distribution of Students' Records.

Overall

Performance

Number of

Students

Cumulative

Relative

GPA ≤ 2.0 0 0.00%

0.00%

2.0 < GPA ≤ 2.7 104 34.10%

34.10%

2.7 < GPA ≤ 3.3 128 76.07%

41.97%

3.3 < GPA ≤ 4.0 73 100.00%

23.93%

Table 2: Snapshot of the Students' Records.

3.2 Identifying the Optimal Regression

Tree

70% of the dataset records were applied to Matlab

CART algorithms with an added 15% for a 10-fold

cross validation. Another innovative approach in our

research was the study of the effect of the splitting

value to the precision of the obtained trees for every

year and for every type. To this purpose, 15% of

untrained data records were used to evaluate the

precision of the trees based on different values of

splitting criteria. For each splitting value, testing was

applied and precision of the estimated GPA was

computed. It is noteworthy to mention that the

splitting value should not exceed a certain value

based on the number of records; otherwise the

precision will degrade in a drastic manner. With a

splitting value of one, the tree will be extremely

cumbersome to read or follow despite the fact that

the precision is very high (near to 99%). The

objective is to choose a compromise that yields a

readable tree or roadmap while keeping an

acceptable precision.

Additionally, correlation is computed solely

based on the testing data in order to accentuate the

credibility and reliability of our model in the choice

of an optimal splitting value for an optimal

regression tree. It will be applied on a double-

column matrix of 15% of the untrained data, thus

comparing estimated GPA with the actual values.

The most familiar measure of dependence between

two quantities is the Pearson product-moment

correlation coefficient, or Pearson's correlation. It is

obtained by dividing the covariance of the two

variables by the product of their standard deviations.

The Pearson correlation is +1 in the case of a perfect

positive (increasing) linear relationship (correlation)

and as it approaches zero there is less of a

relationship (closer to uncorrelated), (Dowdy, and

Wearden, 1983).

3.2.1 Regression Tree for the First Year of

Engineering

In this section, a regression tree was generated for

all the courses taken by engineering students during

their first year of studies. The purpose of this tree is

threefold. First it underlines the key courses that

affect students’ performance with respect to their

performance upon graduation. Second, it shows the

deciding grades that should be obtained in these

courses and which would determine the further

bifurcation and thus, trap students into a descending

subtree. Finally, it estimates their final cumulative



1111111122222222222223333333

ENL230

ENL213

PHS212

CHM211

MAT211

MAT213

MAT215

MAT224

PHS213

MAT235

MAT335

MAT326

CSC212

CSC213

CSC312

EEN201

EEN202

EEN220

EEN210

EEN203

EEN221

EEN311

EEN324

EEN340

EEN344

EEN331

EEN312

EEN325

1.02.72.34.01.73.03.74.01.02.01.01.73.73.32.33.74.03.32.03.33.72.03.32.31.71.72.04.0

2.32.71.02.71.72.32.31.71.72.71.01.01.71.73.32.71.71.71.73.32.31.72.02.01.71.72.33.3

2.33.01.03.01.02.73.02.32.32.71.02.03.33.02.72.01.73.71.71.72.31.72.02.32.02.72.01.7

3.33.02.34.03.34.03.73.72.73.73.73.71.72.73.04.04.03.03.74.04.03.03.03.02.73.04.04.0

2.73.33.73.02.34.01.72.73.03.02.32.73.03.33.33.34.03.33.34.03.72.33.33.33.33.33.03.3

2.72.73.34.02.73.31.02.02.32.73.02.33.03.72.72.33.32.03.04.03.73.03.72.72.73.04.04.0

3.73.73.04.04.04.04.04.04.04.04.04.04.04.04.04.03.74.04.04.04.04.04.04.04.04.04.04.0

3.73.73.74.04.04.04.04.04.04.04.04.04.04.04.04.04.04.04.03.74.04.04.04.04.04.03.74.0

3.73.73.04.04.04.04.04.04.04.04.03.74.04.04.04.04.04.04.04.04.04.04.04.04.04.04.04.0

3.01.74.03.73.04.04.03.73.04.04.04.04.03.34.03.73.74.03.74.04.03.73.33.73.33.34.03.0

2.01.73.72.03.03.73.33.31.73.73.32.74.03.04.02.73.04.03.34.04.02.34.03.02.73.04.04.0

3.02.03.31.73.74.04.03.74.04.01.73.72.03.33.32.33.32.73.34.04.03.03.73.33.73.74.04.0

3.33.73.73.33.33.03.33.73.04.04.04.03.73.74.03.73.33.33.03.73.73.74.03.33.33.73.73.7

1.02.01.02.73.02.02.72.32.32.33.33.73.74.02.73.01.74.02.34.03.73.02.72.32.03.33.33.3

2.32.02.33.02.71.71.31.02.01.31.32.31.71.72.01.72.02.72.33.33.31.71.72.01.72.03.31.7

1.72.71.33.02.32.03.32.01.02.32.03.73.73.32.31.73.32.02.03.33.31.71.72.32.01.72.72.7

2.31.71.02.31.01.02.01.01.32.72.33.03.02.72.03.31.71.72.03.03.72.01.72.02.72.32.74.0

1.03.02.71.03.02.32.31.31.01.71.71.72.72.02.33.03.32.72.04.03.72.32.72.72.72.04.04.0

3.02.02.73.03.03.33.03.33.73.74.03.33.03.03.73.03.32.33.74.04.02.73.33.03.03.03.73.3

3.02.31.72.32.72.72.72.72.73.04.02.02.72.73.02.02.32.72.34.03.32.74.03.03.73.03.73.3

3.72.72.74.03.33.03.73.03.03.04.03.03.34.03.03.03.04.03.04.04.03.03.33.03.33.34.03.7

3.33.32.04.04.04.02.03.32.33.03.02.73.74.03.32.01.73.33.04.04.03.34.04.03.32.34.03.0

3.02.71.73.33.32.73.02.72.03.03.73.03.73.34.03.03.32.33.34.04.03.33.32.32.73.04.04.0

3.73.04.04.04.04.04.04.04.04.04.04.03.34.03.74.04.04.04.04.04.04.03.74.04.04.03.74.0

Academic Year

Student

CreatinganEducationalRoadmapforEngineeringStudentsviaanOptimalandIterativeYearlyRegressionTreeusingData

Mining

GPA upon graduation based on their performance in

these courses.

It should be noted that many trees can be

produced depending on the splitting values. For a

value of one, the tree is cumbersome and contains a

very high number of nodes and branches although it

engenders a high precision. Nonetheless, and to

come up with a readable, yet acceptably reliable

tree, a study of the estimation precision error and

correlation has been conducted as shown below.

To this purpose and for each splitting value, the

difference between the estimated GPA and the actual

one are drafted as shown by figure 1 below. This

error is not calculated in the phases of training or

cross-validation but during the testing phase, i.e.

using new/untrained data. Figure 1 shows that most

of the errors are trapped between -0.3 and +0.3 for

most splitting values.

Figure 1: Estimation Error vs. Number of Students'

Records for Different Splitting Values (Year 1).

In order to endorse and have a different

perspective of this estimation error, Pearson

Correlation was applied on the set of the

aforementioned GPAs. Figure 2 shows that the

correlation is highly acceptable for splitting values

up to 50 beyond which, it starts to significantly

deteriorate. Hence, we had the choice of a splitting

value starting from 1 to 50. However, the number of

nodes and branches and thus, the shape and

readability of the tree are significantly affected

Figure 2: Correlation (Year 1): Estimated GPA vs. Actual

GPA for Different Splitting Values.

After some pertinent comparisons, it was found

that the value of 41 is the most adequate

compromise with a correlation of +0.8 or 80% and

Figure 3 below shows the regression tree obtained in

this case.

Figure 3: Regression Tree (Year 1) for Splitting Value of

41.

3.2.2 Regression Tree for Year “N”

In this section we will examine creating two types of

regression trees for the academic years following the

first year of studies. The first type of tree will

estimate students’ final cumulative GPA (upon

graduation) by exclusively encompassing the

courses taken by students during that year “n”. In the

second type, we will re-inject students’ previous

cumulative GPA in the attributes’ dataset and thus,

consider it as an additional input to the

aforementioned courses. It is understood that one

can create such types of trees of every year of

studies. Nevertheless, this process becomes useless

after the third year and this for two reasons. First,

students would have completed a relatively high

number of credits and thus, reversing or rectifying

their path would reveal impractical if not impossible.

Second, the third year is usually a turning point for

MS studies and/or for BE studies where students

would have to be screened. Therefore, we choose to

demonstrate the results for this particular year

knowing that the same procedure has been done for

the second year as well but it would not add new

information to this text.

Figures 4, 5 and 6 show the same results

obtained as for Year 1 but applied to Year 3 for the

first type of tree, i.e. without taking into account

students’ current cumulative GPA. The purpose of

the tree obtained is to pinpoint those courses taken in

Year 3 and which have greater impact on students’

later performance.

0.6 5

0.7 0

0.7 5

0.8 0

0.8 5

0.9 0

0.9 5

1.0 0

0 20406080100120140

Splitting Value s

Correlation

3.515

3.2541

3.172.9004

2.835

2.5332

2.48882.29

2.7421

2.8548

3.33

3.759

CHM211

PHS212MAT215

MAT224

MAT213MAT211MAT211

MAT224

MAT211

ENL230

≥3.15

<3.15

<3.15 ≥3.15

≥3.15

<3.15

<2.15 ≥2.15

≥3.85

<3.85

<3.5 ≥3.5

<2.5

<2.5 <2.5

≥2.5

≥2.5<2.5

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

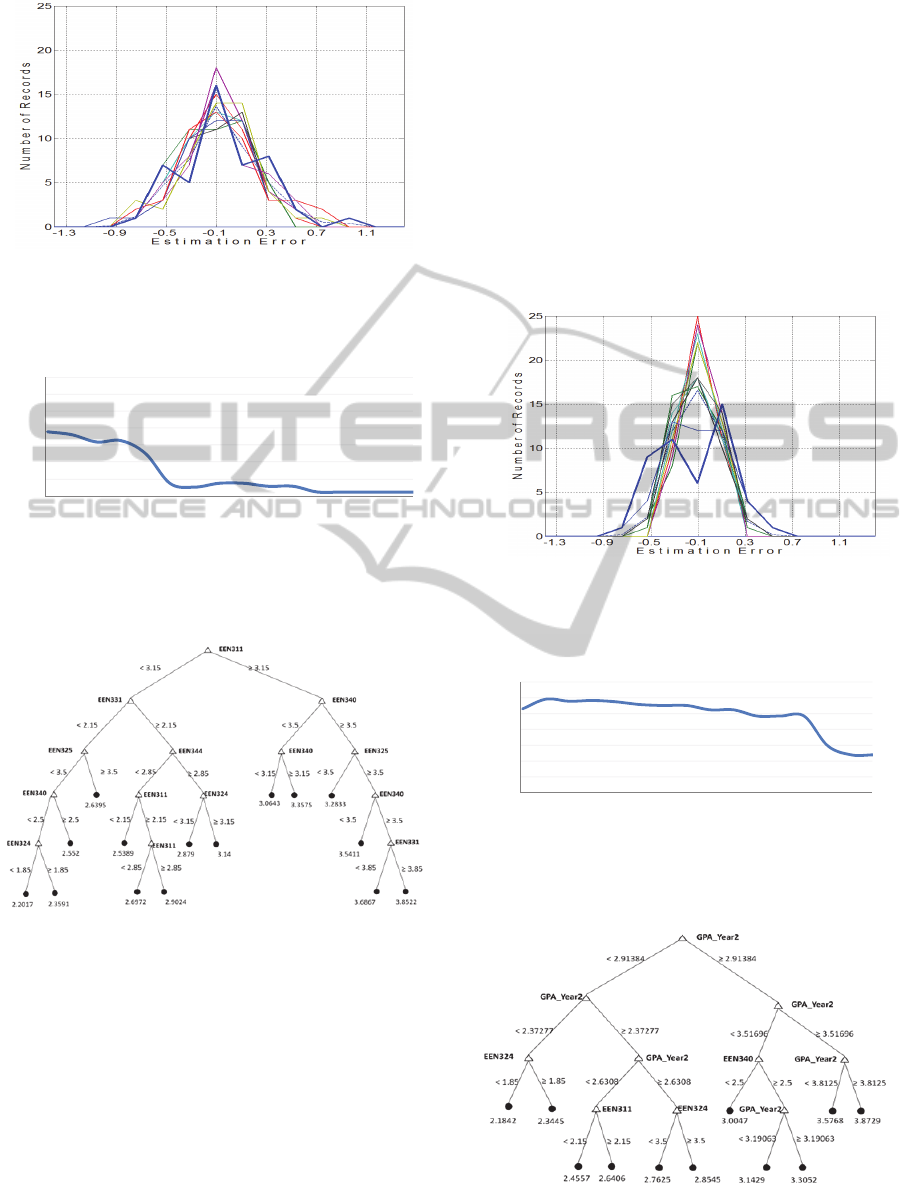
Figure 4: Estimation Error vs. Number of Students'

Records for Different Splitting Values (Year 3).

Figure 5: Correlation (Year 3): Estimated GPA vs. Actual

GPA for Different Splitting Values.

Figure 6: Regression Tree (Year 3) for Splitting Value of

41.

The figures below exhibit the iterative (second)

type of trees that take into account students’

previous cumulative GPA vs. their GPA upon

graduation. As it is expected, the most preponderant

determining factor (tree node) is the GPA computed

up to Year 2. This greatly endorses the credibility

and reliability of the study. Indeed, it clearly proves

that after two years of studies and thus, with more

than 70 credits accomplished, it would be

realistically difficult to modify a cumulative GPA in

a significant manner with new courses taken; the

GPA is a ratio with its denominator becoming

relatively bigger. Nonetheless, the obtained tree is

again a clear roadmap since it allows students and

advisors to identify which track (or subtree) they

would be following based on previous history.

Consequently, students can be advised to repeat

some courses in order to increase their current

cumulative GPA to start from a different node

according to a desired final performance upon

graduation. This is a powerful tool for advising and

follow-up on all cases.

Figure 7, 8, and 9 below show the results of

similar analysis and studies performed as above.

Figure 7: Estimation Error vs. Number of Students'

Records with Year-2 Cumulative GPA Injected (Year 3).

Figure 8: Correlation (Year 3) with Cumulative Year-2

GPA Injected.

Figure 1: Regression Tree (Year 3) for Splitting Value of

41 with Year-2 Cumulative GPA Injected.

0.6 5

0.7 0

0.7 5

0.8 0

0.8 5

0.9 0

0.9 5

1.0 0

0 20406080100120140

Splitting Values

Correlation

0.6 5

0.7 0

0.7 5

0.8 0

0.8 5

0.9 0

0.9 5

1.0 0

0 20406080100120140

SplittingValues

Correlation

CreatinganEducationalRoadmapforEngineeringStudentsviaanOptimalandIterativeYearlyRegressionTreeusingData

Mining

3.2.3 Result Analysis of the Educational

Roadmap – Advisors’ and Students’

Manual

Upon enrolling in engineering majors, students are

provided with a suggested or recommended first-

year curriculum to follow. Moreover, some courses

are enforced in the sense that they have to be taken

by students because either they are prerequisites for

later courses or according to each department’s

vision, students should pass these courses for

specific academic purposes. In any case,

performance in these courses will certainly have an

impact on students cumulative GPA as well on their

GPA upon graduation. Therefore, according to the

suggested tree, students and advisors can identify

those courses to be paid attention to and even

suggest a new “minimum passing grade” in order to

aim at a targeted final GPA. Moreover, the tree can

be used in a bottom-up manner in the sense that

students can start at the bottom, thus selecting a

targeted final GPA and work their way up going

through those nodes that decide of this choice and

hence, know in advance the performance required in

those powerful or key courses which have greater

impact on their target. In this manner, the suggested

trees constitute an educational roadmap and a

manual to be used by advisors and students to keep

track of their academic path.

This also applies to the remaining years of

engineering curricula. However, the second type of

trees which take into account a current cumulative

GPA injected in the attributes, allow a further and

wider look at the students’ path. It allows advisors to

rectify on a yearly basis and before “it is too late”

the courses and their respective grades students

should accomplish in order to attain their targeted

GPA upon graduation. For instance, if a second- or

third- year engineering student earn a GPA lower

than the one expected, rectifying steps can be

advised with lesser damage and efforts and namely

within shortest time. Finally, probation, suspension

or even keeping grants and scholarships can be

handled more efficiently based on enlightened

decisions.

The trees can be used in a cooperative manner

between the advisors and the students in line with

the importance given to the academic advising in the

higher educational process (Campell, 2008). As was

mentioned “academic advising supports key

institutional conditions that have been identified

with promoting student success”. In addition, as it

was noted by Titno (Titno, 2012)the five conditions

which stand out as supportive of retention were

expectation, advice, support, involvement, and

learning.

Our regression trees can be considered as a tool

used by both the academic advisor and the student to

schematize, evaluate and direct the road map of the

graduation requirements in an interactive method.

The purpose of not implementing the application as

an automated one similar to the work performed by

Werghi and Kanoun (Werghi and Kanoun, 2010) is

the importance we give to the interactive

cooperation between the advisor and the student in

order to achieve academic excellence. Consequently,

the approach presented in this paper, not only

emphasises on this trend, but offers a more

comprehensive and flexible tool as well.

4 PERSPECTIVE WORK - EVA

Earned Value Analysis (EVA) has proven to be an

extremely effective tool for project time and cost

management providing actual project completion

cost and date. One main contribution of EVA is

providing early indicators of problem areas either in

cost or in schedule so that corrective management

can be initiated (Leu and Lin, 2008), (Henderson,

2004). Other areas were tackled as well in order to

extend EVA analysis to fuzzy control or quality

evaluation (Noori et al., 2008), (Hong-yuan et al.,

2007).

EVA is used in combination with the estimation

of the cost and delivery date. In the educational

environment, the engineering degree can be

considered as a project with a specific estimated

time (measured in number of credits successfully

accomplished) and an estimated GPA upon

graduation.

In our case, the study duration is considered as

the five-year comprehensive curriculum (or 10

semesters); cumulative GPA as well as the number

of credits passed are computed at the end of each

semester. Target values of the aforementioned

parameters are specified by students at their

enrolment, and evaluation is performed to check

whether they are on the right track. In case of

deviation, the objective will be to

materialize/quantify this deviation from the targets’

starting values.

Pertinent parameters are derived in order to keep

track of students’ evolution such as Earned Values,

Credit Variance, Scheduled Variance, Performing

Index, and Schedule Index, amongst others.

The importance of the aforementioned

parameters is that they provide an accurate and

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

continuous evaluation of the efforts performed by

each student and a clear measure of their efficiency

in attaining the targeted starting values. More

specifically, these parameters can be appropriately

used to derive specific suggestion as rectify each

student’s path when calibration reveals necessary.

Finally, it is important to note that EVA analysis,

tools and charts would be a significant addition to

the educational roadmap developed in this paper.

5 CONCLUSIONS

In this paper we have presented an innovative

approach in using and applying Educational Data

Mining. An educational roadmap that reliably and

greatly endows both advisors and students a

straightforward manual for success. This roadmap is

built using Regression Trees with different types

elaborated in the frame of a continuous and close

follow-up of students’ performance. Correlation

Analysis and study of different splitting values of

the regression tress were extensively examined to

choose the best readable and useful tree/roadmap

while keeping a high rate of precision in the

estimation process. In this context, two types of trees

were developed and elaborately analyzed. The first

type identifies, on a yearly-basis, courses and their

respective grades which have greater impact on

students’ cumulative GPA upon graduation. The

second type is an iterative tree that re-injects the

current students’ GPA into the dataset as an

additional attribute. This proved to be a powerful

tool for decision making and endorsed the results

and the computed precision. The trees were trained,

cross-validated and tested. Calculation of the

precision and Correlation Analysis were achieved

based on untrained data to significantly enhance the

reliability of the outcome. Also a detailed

perspective of this study was presented under Earned

Value Analysis as a future scope of work and an

added tool for advising and monitoring students’

efforts, performance and evolution throughout their

engineering curricula.

REFERENCES

Kovačić, Z., Green, J., 2010, Research in Higher

Education Journal, Predictive working tool for early

identification of ‘at risk’ students, Open Polytechnic,

Wellington, New Zealand.

Sembiring, S., Zarlis, M., Hartama, D., Ramliana, S.,

Wani, E., 2011, International Conference on

Management and Artificial Intelligence, Prediction of

Student Academic Performance by an Application of

Data Mining Techniques, IACSIT Press vol. 6.

Wook, M., Yahaya, Y., Wahab, N., Isa, M., Awang, N. F.,

Seong, H. Y., 2009, In Proceedings of the Second

International Conference on Computer and Electrical

Engineering, Predicting NDUM Student’s Academic

Performance Using Data Mining Techniques, IEEE

computer society.

Al-Radaideh, Q., Al-Shawakfa, E., Al-Najjar, M. I., 2006,

The 2006 International Arab Conference on

Information Technology, ACIT'2006, Mining Student

Data Using Decision Trees.

Kovačić, Z., 2010, Proceedings of Informing Science & IT

Education Conference (InSITE). Early Prediction of

Student Success: Mining Students Enrolment Data

Portnoi, L. M., & Kwong, T. M., 2011, Journal of Student

Affairs Research and Practice, volume 48, No. 4.,

Enhancing the academic experiences of first-

generation master’s students.

Oladokun, V. O., Adebanjo, A. T., Charles-Owaba, O. E.,

2008, The Pacific Journal of Science and Technology,

Volume 9. Number 1., Predicting Students’ Academic

Performance using Artificial Neural Network: A Case

Study of an Engineering Course

Chadha, A., Kumar, V., 2011, International Journal of

Advanced Computer Science and Applications, Vol. 2,

No. 3., An Empirical Study of the Applications of Data

Mining Techniques in Higher Education

Pal, S., Baradwaj, B. K., 2011, International Journal of

Advanced Computer Science and Applications, Vol. 2,

No. 6., Mining Educational Data to Analyze Students’

Performance

Eshghi, A., Haughton, D., Li, M., Senne, L., Skaletsky M.,

Woolford, S., 2011, Journal of Institutional Research,

vol. 16, No.2., Enrolment Management in Graduate

Business Programs: Predicting Student Retention

Dowdy, S. Wearden, S., 1983, Statistics for Research,

Wiley. ISBN 0471086029 pp 230.

Domingos, P., 2007, Proceedings of Data Min. Knowledge

and Discovery, 21-28, Volume 15, Issue 1., Toward

Knowledge-Rich Data Mining

Fayyad, U. M.; Piaetsky-Shapiro, G.; Smyth, P., 1996,

Advances In Knowledge Discovery and Data Mining,

From Data Mining to Knowledge Discovery: An

Overview. AAAI/MIT press, Cambridge mass.

Witten, I. H., Frank, E., Hall, M. A., 2011, Data Mining:

Practical Machine Learning Tools and Techniques.

Morgan Kaufmann, Third Edition.

J., Han, M., Kamber, J., Pei, 2011, Data Mining: Concepts

and Techniques, Morgan Kaufmann, Third Edition.

Nock, R., Nielsen, F., 2006, IEEE Trans. on Pattern

Analysis and Machine Intelligence, Vol. 28, No. 8, On

Weighting Clustering, August 2006, p. 1–13.

Agrawal; R., Imielinski; T., Swami, A., 1993, Proceedings

of the ACM SIGMOD International Conference on

Management of Data, Mining Association Rules

between Sets of Items in Large Databases

Piatetsky-Shapiro, G., 1991, Knowledge Discovery in

Databases, Discovery, analysis, and presentation of

CreatinganEducationalRoadmapforEngineeringStudentsviaanOptimalandIterativeYearlyRegressionTreeusingData

Mining

strong rules, in G. Piatetsky-Shapiro & W. J. Frawley,

AAAI/MIT Press, Cambridge, MA.

Denning, D., 1986, IEEE Transactions on Software

Engineering - Special issue on computer security and

privacy, An Intrusion-Detection Model,

Getoor, L., 2003, ACM SIGKDD Explorations, Vol.5,

No.1. , Linking Mining: A New Data Mining

Challenge

Silverstein, C., Brin, S., Motwani, R., Ullman, J., 2000,

Data Mining and Knowledge Discovery, Volume 4,

Numbers 2-3, Scalable Techniques for Mining Causal

Structures

Quinlan, J. R., 1986, Machine Learning, 1:81-106,

Induction of Decision Trees

Thabtah, F., 2006, Journal of Digital Information

Management, vol. 4, no. 3, pp. 197-202., Pruning

Techniques in Associative Classification: Survey and

Comparison.

Baker, R. S. J. d., Yacef, K., 2009, Journal of Educational

Data Mining, vol. 1, issue 1, pp. 3-17., The State of

Educational Data Mining in 2009: A Review and

Future Visions

Al-Radaideh, Q., Al Ananbeh, A., Al-Shawakfa, E., 2011,

IJRAS volume 8, issue 2., A classification model for

predicting the suitable study track for school students

Dekker, G., Pechenizki, M., Vleeshouwers, J., 2009,

Proceedings of the Educational Data mining.

Predicting Students Drop Out: A Case Study

Bardawaj, B. K., Pal, S., 2011, International Journal of

Advanced Computer Science and Applications, vol 2,

issue 6. Mining Educational Data to Analyze Student’s

Performance

Kabra R., Bichkar, R., 2011, International Journal of

Computer Applications, volume 36, No 11, December.

Performance Prediction of Engineering Students using

Decision Trees

Noori, S., Bagherpour, M., Zareei, A., 2008, World

Applied Sciences Journal 3(4). Applying Fuzzy

Control Chart in Earned Value Analysis: A New

Application

Hong-yuan, F., Chuang-bin, H., Lang, Z., 2007, Journal of

Chongking University. Quality Earned Value Method

Based on Quality Evaluation

Camplell, S., 2008, Association of American Colleges and

Universities Peer Review, winter 2008, vol. 10, No 1.

Academic Advising in the new global Century:

Supporting Student Engagement and Learning

Outcomes Achievement

Tinto, V., 2012, Taking Student Retention Seriously,

retrieved from hxxp://faculty.soe.syr.edu/vtinto/

Files/Taking Student Retention Seriously.pdf, July

2012.

Werghi, N., Kamoun, F., 2010, International Journal of

Business Information Systems, Vol. 5, No. 1, pp 1-18.

A Cecision-Tree Based System for Student Academic

Advising and Planning in Information Systems

Programmes

Leu S., Lin Y., 2008, Journal of Construction Engineering

and Management. Project Performance Evaluation

Based on Statistical Process Control Techniques

Henderson K., 2004, The Measurable News. Further

Developments in Earned Schedule

Wu X., Kumar V., 2009, The Top Ten Algarithms in Data

Mining, CRC Press, Taylor & Francis Group.

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment