Ontology Enrichment based on Generic Basis of Association Rules for

Conceptual Document Indexing

Lamia Ben Ghezaiel

, Chiraz Latiri

and Mohamed Ben Ahmed

Computer Sciences School, RIADI-GDL Research Laboratory, Manouba University, 2010, Tunis, Tuni

sia

LIPAH Research Laboratory, Computer Sciences Department, Faculty of Sciences of Tunis,

El Manar University, 1068, Tunis, Tunisia

Keywords:

Text Mining, Ontology Enrichment, Information Retrieval, Association Rule, Generic Basis, Distance

Measures, Conceptual Indexing.

Abstract:

In this paper, we propose the use of a minimal generic basis of association rules (ARs) between terms, in

order to automatically enrich an initial domain ontology. For this purpose, three distance measures are deﬁned

to link the candidate terms identiﬁed by ARs, to the initial concepts in the ontology. The ﬁnal result is a

proxemic conceptual network which contains additional implicit knowledge. Therefore, to evaluate our ontol-

ogy enrichment approach, we propose a novel document indexing approach based on this proxemic network.

The experiments carried out on the OHSUMED document collection of the TREC 9 ﬁltring track and MeSH

ontology showed that our conceptual indexing approach could considerably enhance information retrieval

effectiveness.

1 INTRODUCTION

Recently, several research communitiesin text mining

and semantic web spent a determined efforts to con-

ceptualize competencies of a given domain through

the deﬁnition of a domain ontology. However, in or-

der to make that ontology actually of use in applica-

tions, it is of paramountimportanceto enrich its struc-

ture with concepts as well as instances identifying the

domain.

Many contributions in the literature related to In-

formation Retrieval (IR) and text mining ﬁelds proved

that domainontologies are very useful to improvesev-

eral applications such as ontology-based IR models

(Song et al., 2007). While several ontology learning

approaches extract concepts and relation instances di-

rectly from unstructured texts, in this paper, we show

how an initial ontology can be automatically enriched

by the use of text mining techniques. Especially, we

are interested in mining a speciﬁc domain document

collections in order to extract valid association rules

(Agrawal and Skirant, 1994) between concepts/terms.

Thus, we propose to use a minimal generic basis of

association rules, called M G B , proposed in (Latiri

et al., 2012), to detect additional concepts for expand-

ing ontologies. The result of our enrichment process

is a proxemic conceptual network, denoted O

M G B

which unveils the semantic content of a document.

To show the beneﬁts of this proxemic conceptual net-

work in the IR ﬁeld, we propose to integrate it in a

document conceptual indexing approach.

The remainder of the paper is organized as fol-

lows: Section 2 recalls paradigms for mining generic

basis of association rules between terms. In Section

3, we brieﬂy present related works dedicated to the

enrichment of ontology. Section 4 introduces a novel

automatic approach of ontology enrichment based on

the generic basis M G B . Section 5 presents a doc-

ument conceptual indexing approach based on the

enriched ontology O

M G B

. Section 6 is devoted to

the experimental evaluation, in which the results of

the carried out experiments on OHSUMED collection

and MeSH ontology are discussed. The conclusion

and work in progress are ﬁnally presented in Section

2 GENERIC BASIS OF

ASSOCIATION RULES

In a previous work (Latiri et al., 2012), we used in the

text mining ﬁeld, the theoretical framework of Formal

Concept Analysis (FCA), presented in (Ganter and

Ben Ghezaiel L., Latiri C. and Ben Ahmed M..

Ontology Enrichment based on Generic Basis of Association Rules for Conceptual Document Indexing.

DOI: 10.5220/0004131600530065

In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2012), pages 53-65

ISBN: 978-989-8565-30-3

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

Wille, 1999), in order to propose the extraction of a

minimal generic basis of irredundantassociation rules

between terms, named M G B (Latiri et al., 2012).

2.1 Mathematical Foundations and

Basic Deﬁnitions

First, we formalize an extraction context made up of

documents and index terms, called textual context.

2.1.1 Textual Context

Deﬁnition 1. A textual context is a triplet M =

(C , T , I ) where:

• C = {d

, d

, . . . , d

} is a ﬁnite set of n documents

of a collection.

• T = {t

, ·· · , t

} is a ﬁnite set of m distinct

terms in the collection. The set T then gathers

without duplication the terms of the different doc-

uments which constitute the collection.

• I ⊆ C × T is a binary (incidence) relation. Each

couple (d, t) ∈ I indicates that the document d ∈

C has the term t ∈ T .

Table 1: An example of textual context.

I A C D T W

× × × ×

× × ×

× × × ×

× × × × ×

× × ×

Example 1. Consider the context given in Table 1,

used as a running example through this paper and

taken from (Zaki, 2004). Here, C = {d

, d

} and T := {A, C, D, T, W}. The couple (d

C) ∈ I since it is crossed in the matrix. This denotes

that the document d

contains the term C.

Each document d ∈ C is represented by a binary

vector of length m. A termset T can be interpreted

as a set of m terms T ∈ T , that occur together in the

document. For example, ACW is a termset composed

by the terms A, C and W. The support of a termset is

deﬁned as follows:

Deﬁnition 2. Let T ⊆ T . The support of T in M

is equal to the number of documents in C containing

all the terms of T. The support is formally deﬁned as

follows

(1)

In this paper, we denote by |X| the cardinality of the set

Supp(T) = |{d | d ∈ C ∧ ∀ t ∈ T : (d, t) ∈ I }| (1)

A termset is said frequent (aka large or covering)

if its terms co-occur in the collection a number of

times greater than or equal to a user-deﬁned support

threshold, denoted minsupp.

2.1.2 Galois Closure Operator

Two functions are deﬁned in order to map sets of doc-

uments to sets of terms and vice versa. Thus, for

T ⊆ T , we deﬁned (Ganter and Wille, 1999):

Ψ(T) = {d|d ∈ C ∧ ∀ t ∈ T : (d, t) ∈ I } (2)

Ψ(T) is equal to the set of documents containing

all the terms of T. Its cardinality is then equal to

Supp(T).

For a set D ⊆ C , we deﬁne:

Φ(D) = {t|t ∈ T ∧ ∀ d ∈ D : (d, t) ∈ I } (3)

Φ(D) is equal to the set of terms appearing in all the

documents of D.

Both functions Ψ and Φ constitute Galois opera-

tors between the sets P (T ) and P (C ). Consequently,

the compound operator Ω = Φ◦ Ψ is a Galois closure

operator which associates to a termset T the whole

set of terms which appear in all documents where the

terms of T co-occur. This set of terms is equal to

Ω(T). In fact, Ω(T) = Φ◦ Ψ(T) = Φ(Ψ (T )). If Ψ

(T) = D, then Ω(T) = Φ(D).

Example 2. Consider the context given in Table 1.

Since both terms A and C simultaneously appear in

the documents d

, d

, and d

, we have: Ψ(AC) =

, d

}. On the other hand, since the docu-

ments d

, d

, and d

share the terms A, C, and W,

we have: Φ({d

, d

}) = ACW. It results that

Ω(AC) = Φ ◦ Ψ(AC) = Φ(Ψ(AC)) = Φ({d

, d

})= ACW. Thus, Ω(AC) = ACW. In other words,

the term W appears in all documents where A and C

co-occur.

2.1.3 Frequent Closed Termset

A termset T ⊆ T is said to be closed if Ω(T) =

T. A closed termset is then the maximal set of

terms common to a given set of document. A closed

termset is said to be frequent w.r.t. the minsupp

threshold if Supp(T) = |Ψ(T)| ≥ minsupp (Bastide

et al., 2000). Hereafter, we denote by FCT a frequent

closed termset.

Example 3. With respect to the previous example,

ACW is a closed termset since there is not another

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

term appearing in all documents containing ACW.

ACW is then the maximal set of terms common to the

documents {d

, d

}. We then have: Ω(ACW)

= ACW. If minsupp is set to 3, ACW is also frequent

since |Ψ (ACW)|=|{d

, d

}| = 4 ≥ 3.

The next property states the relation between the

support of a termset and that of its closure.

Property 1. The support of a termset T is equal to

the support of its closure Ω(T ), which is the small-

est FCT containing T, i.e., Supp(T) = Supp(Ω(T))

(Bastide et al., 2000).

2.1.4 Minimal Generator

A termset g ⊆ T is a minimal generator of a closed

termset T, if and only if Ω(g) = T and ∄ g

′

⊂ g:

Ω(g

′

) = T (Bastide et al., 2000).

Example 4. The termset DW is a minimal generator

of CDW since Ω(DW) = CDW and none of its proper

subsets has CDW for closure.

Corollary 1. Let g be a minimal generator of a fre-

quent closed termset T. According to Property 1, the

support of g is equal to the support of its closure, i.e.,

Supp(g) = Supp(T).

2.1.5 Iceberg Lattice

Let F C T be the set of frequent closed termsets of

a given context. When the set F C T is partially or-

dered w.r.t. set inclusion, the resulting structure only

preserves the Join operator (Ganter and Wille, 1999).

This structure is called a join semi-lattice or an upper

semi-lattice, and is hereafter referred to as Iceberg lat-

tice (Stumme et al., 2002).

In (Latiri et al., 2012), we presented an approach

that relies on irredundant association rules mining

starting from the augmented Iceberg lattice, denoted

by A L = (F C T , ⊆), which is the standard Iceberg

lattice where each FCT is associated to its minimal

generators.

Example 5. Consider the context given in Table 1.

The minsupp threshold is set to 3. The associated

augmented Iceberg lattice is depicted in Figure 1,

in which the minimal generators associated to each

FCT are given between brackets.

Each frequent closed termset T in the Iceberg lat-

tice has an upper cover which consists of the closed

termsets that immediately cover T in the Iceberg lat-

tice. This set is formally deﬁned as follows:

Cov

(T) = {T

∈ F C T | T ⊂ T

and ∄ T

∈ F C T :

T ⊂ T

⊂ T

}

(C)

(W)

ACW

(A)

(D)

(T)

(AT/TW)

ACTW

(DW)

CDW

CWA CTW

T ACW

C T

C D

4/6

3/4 3/4

3/5

ACT

3/4

C AW

4/6

W CD

3/5

Figure 1: The augmented Iceberg lattice.

Example 6. Let us consider the frequent closed

termset CW of the Iceberg lattice depicted by Figure

1. Then, we have: Cov

(CW) ={ACW, CDW}.

2.2 Association Rules Mining

An association rule R is an implication of the form

R: T

⇒ T

, where T

and T

are subsets of T , and

∩ T

0. The termsets T

and T

are, respectively,

called the premise and the conclusion of R. The rule

R is said to be based on the termset T equal to T

∪

. The support of a rule R: T

⇒ T

is then deﬁned

as:

Supp(R) = Supp(T) (4)

while its conﬁdence is computed as:

Conf(R) =

Supp(T

)

Supp(T)

(5)

An association R is said to be valid if its conﬁ-

dence value, i.e., Conf(R), is greater than or equal to a

user-deﬁned threshold denoted minconf

(2)

. This con-

ﬁdence threshold is used to exclude non valid rules.

Example 7. Starting from the context depicted in Ta-

ble 1, the association rule R: W ⇒ CD can be de-

rived. In this case, Supp(R) = Supp(CDW) = 3, while

Conf (R) =

Supp(CDW)

Supp(W)

. If we consider the min-

supp and minconf thresholds respectively equal to 3

and 0.5, the considered rule R is valid since Supp(R)

= 3 ≥ 3 and Conf (R) =

≥ 0.5.

2.3 Minimal Generic Basis of

Association Rules

Given a document collection, the problem of min-

ing association rules between terms consists in gen-

In the remainder, T

⇒ T

indicates that the rule T

⇒

has a value of conﬁdence equal to c.

OntologyEnrichmentbasedonGenericBasisofAssociationRulesforConceptualDocumentIndexing

erating all association rules given user-deﬁned min-

supp and minconf thresholds. Several approaches

in the literature deal with the redundancy problem.

More advanced techniques that produce only a lim-

ited number of rules rely on Galois closure (Ganter

and Wille, 1999). These techniques focus on extract-

ing irreducible nuclei of all association rules, called

generic basis, from which the remaining associa-

tion rules can be derived (Bastide et al., 2000; Latiri

et al., 2012). An interesting discussion about the main

generic bases of association rules is proposed in (Ben

Yahia et al., 2009; Balc´azar, 2010; Latiri et al., 2012).

However, the huge number of irredundant associ-

ation rules constitutes a real hamper in several appli-

cations related to text mining. To overcome this prob-

lem, we proposed in (Latiri et al., 2012) the use of a

minimal generic basis, called M G B , based on the ex-

traction of the augmented Iceberg lattice. This basis

involves rules that maximize the number of terms in

the conclusion. We distinguish two types of associ-

ation rules: exact association rules (with conﬁdence

equal to 1) and approximate association rules (with

conﬁdence less than 1)(Zaki, 2004).

Hence, in the following, we will adapt the Mini-

mal GenericBasis M G B of association rules, deﬁned

in (Latiri et al., 2012), to enrichment ontology issue.

When considering a textual context M := (C , T , I ),

the minimal generic basis M G B is deﬁned as fol-

lows:

Deﬁnition 3. Given A L an Iceberg Galois lattice

augmented by minimal generators and their supports,

a frequent closed termset, Cov

) its upper cover

and G

the list of its minimal generators of the fre-

quent closed termset T

, we have:

M G B =











R : g → (T

− g) | g ∈ G

∧ T

∈ A L

∧

Conf(R) ≥ minconf ∧ ∄ s ∈ Cov

) |

support(s)

support(g)

≥ minconf

(6)

In our approach, the augmented Iceberg lattice

A L supportsthe irredundant association rules discov-

ery between terms. The main advantage brought by

this partially ordered structure is the efﬁciency. In

fact, by using such a precedence order, irredundant

exact and approximate association rules are directly

derived, without additional conﬁdence measure com-

putations.

The GEN-MGB algorithm which allows the con-

struction of the M G B generic basis is detailed in

(Latiri et al., 2012). It iterates on the set of frequent

closed termsets F C T of the augmented Iceberg lat-

tice A L , starting from larger FCTs and sweeping

downwardly w.r.t. set inclusion ⊆. The algorithm

takes the augmented Iceberg lattice A L as input and

gives as output the irredundant approximate and ex-

act association rules (i.e., IARs and IERs). With re-

spect to Equation (6) and considering a given node in

the Iceberg lattice, we consider that IARs represent

implications that involve the minimal generators of

the sub-closed-termset, associated to the considered

node, and a super-closed-termset. On the other hand,

IERs are implications extracted using minimal gen-

erators and their respective closures, belonging to the

same node in A L (Latiri et al., 2012).

Example 8. Consider the augmented Iceberg lattice

depicted in Figure 1 for minconf = 0.6. Let us re-

call that the set value of minsupp is equal 3. All irre-

dundant approximate association rules are depicted

in Figure 1. In this case, none irredundant exact rule

is mine since all of them are redundant w.r.t. irre-

dundant approximate rules belonging to M G B . For

example, starting from the node having CDW for fre-

quent closed termset, the exact rule DW

⇒ C is not

generated since it is consideredas redundantw.r.t. the

approximate association rule D

0.75

⇒ CW.

In this regard, we propose in this paper to disclose

how that can be achieved when a domain ontology is

enriched using irredundant association rules belong-

ing to M G B .

3 RELATED WORKS TO

ENRICHMENT ONTOLOGY

In the literature, there is no common formal deﬁnition

of what an ontology is. However, most approaches

share a few core items: concepts, a hierarchical is-a-

relation, and further relations. For sake of generality,

we formalize an ontology in the following way (Cimi-

ano et al., 2004):

Deﬁnition 4. An ontology is a tuple O = hC

, ≤

, R , ≤

i, where C

is a set whose elements are called

concepts of a speciﬁc domain, ≤

is a partial order

on C

(i.e., a binary relation is-a ⊆ C

× C

), R is a

set whose elements are called relations, and ≤

is a

function which assigns to each relation name its arity.

Throughout this paper, we will consider the Def-

inition 4 to designate a speciﬁc domain ontology. It

is thus considered as a structured network of con-

cepts extracted from a speciﬁc domain and intercon-

nects the concepts by semantic relations. Naturally,

the constructionof an ontologyis hard and constitutes

an expensive task, as one has to train domain experts

in formal knowledge representation. This knowledge

is usually evolvable and therefore an ontology main-

tenance process is required (Valarakos et al., 2004;

Di-Jorio et al., 2008) and plays a main role as ontolo-

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

gies may be misleading if they are not up to date. In

the context of ontologymaintenance, we tackle in this

paper, the problem of enrichment of an initial ontol-

ogy with additional concept derived from a compact

set of irredundant association rules.

Roughly speaking, ontology enrichment process

is performed in two main steps namely: a learning

step to detect new concepts and relations and a place-

ment step which aims to ﬁnd the appropriate place of

these concepts and relations in the original domain

ontology. Several works in literature were proposed

to handle the two previous steps. In this work, we

focus on methods dedicated to the discovery of new

candidate terms from text and their relation with ini-

tial concepts in a domain ontology.

Thereby, two main classes of methods have been

explored for detecting candidate terms, namely (Di-

Jorio et al., 2008):

• Statistical based Methods. They consist in count-

ing the number of occurrences of a given term in

the corpus. Most of the statistical methods select

candidate terms with respect to their distribution

in the corpus (Faatz and Steinmetz, 2002; Parekh

et al., 2004), as using other measures such as test

mutual information, tf-idf (Neshatian and Hejazi,

2004), T-test or statistic distribution laws. These

methods allow to identify the new concepts but

they are not able to add them into the original on-

tology without the help of the domain expert (Di-

Jorio et al., 2008).

• Syntactic based Methods. They require a gram-

matical sentence analysis. Most of these meth-

ods include upstream a part of speech tagging pro-

cess. They assume that grammatical dependencies

reﬂect semantic dependencies (Bendaoud et al.,

2008). In (Maedche et al., 2002; Navigli and Ve-

lardi, 2006), authors introduced the use of lexico-

syntactic patterns to detect ontological relations.

However, to overcome the problem of huge num-

ber of related terms extracted, data mining tech-

niques are applied in some approaches such as

association rules discovery from the syntactic de-

pendencies (Benz et al., 2010). So, association

rules based approaches allow strong correlations

detection. They highlight frequent grammatical

dependencies and thus are a good way to prune

many insigniﬁcant dependencies through the met-

rics of support and conﬁdence and pruning irre-

dundant associations rules (Balc´azar, 2010). The

ﬁrst advantage of the syntactic based methods

compared to statistical based ones is that they al-

low to put automatically new terms into the initial

ontology. Nevertheless, they do not label new re-

lations.

4 ONTOLOGY ENRICHMENT

BASED ON A GENERIC BASIS

OF ASSOCIATION RULES

We propose in this paper a fully automatic process

to expand a given ontology, based on the minimal

generic basis association rules M G B , deﬁned in Sub-

section 2.3. Indeed, we propose to use association

rules between terms to discover new concepts and re-

lations which link them to other concepts. We aim to

enhance the knowledge captured in a domain ontol-

ogy, leading to a proxemic conceptual network to per-

form then conceptual indexing in IR. The main moti-

vation behind the idea, that for a given domain ontol-

ogy, we focus on ﬁnding out automatically uniquely

relevant concepts for enrichment by using irredun-

dant association rules between terms. This allows

to reduce the huge number of related terms extracted

by removing redundant association rules during the

derivation process. For this, we propose to:

1. Generate a minimal generic basis of irredundant

rules M G B from a speciﬁc document collection

to the domain;

2. Detect a set of candidate concepts from the ba-

sis M G B . This implies that an ontology-based

approach is needed to calculate the semantic dis-

tances between the candidate concepts;

3. Select a subset of those candidate concepts with

respect to their neighborhood to concepts already

existing in the original domain ontology;

4. Add new concepts to the ontology;

5. Build a proxemic conceptualnetwork from the en-

riched ontology in order to perform then concep-

tual document indexing in IR.

We assume that we have, for a given domain, a

document collection denoted C . Before mining the

generic basis M G B , we need to generate the textual

context M = (C , T , I ) from the collection C . Hence,

in order to derivethe generic basis of association rules

between terms M G B from our textual context M, we

used the algorithm GEN-MGB to get out irredundant

associations between terms (i.e., approximative and

exact ones) (Latiri et al., 2012).

Furthermore, we consider an initial domain on-

tology denoted by O , such as the medical ontology

MeSH (D´ıaz-Galiano et al., 2008). A such ontology

includes the basic primitives of an ontology which

are concepts and taxonomic relations such as the sub-

somption link is-a. Then, to evaluate the strength of

the semantic link between two concepts inside the on-

tology O , we use Wu and Palmer’s similarity mea-

sure (Wu and Palmer, 1994). It is a measure between

OntologyEnrichmentbasedonGenericBasisofAssociationRulesforConceptualDocumentIndexing

concepts in an ontology restricted to taxonomic links.

Given two concepts C

and C

, Wu and Palmer’s sim-

ilarity measure is deﬁned as follow (Wu and Palmer,

1994):

Sim

) =

2× depth(C)

depth(C

) + depth(C

)

(7)

where depth(C

) is the distance which separates the

concept C

to the ontology root and C is the common

concept ancestor of C

and C

in the given ontology.

4.1 Enrichment Ontology Process

Our enrichment process aims to bring closer the origi-

nal ontology O of the terms contained in the premises

of M G B association rules. Once the new concepts

placed in the ontology, we calculate the different dis-

tance measures which evaluate the semantic links ex-

isting between the concepts of enriched ontology, de-

noted in the sequel by O

M G B

The M G B -based enrichment process iterates

through the following steps.

4.1.1 Step 1: Detecting Candidate Concepts for

Enrichment

We calculate for each concept C

in the initial ontol-

ogy O , the set of candidate concepts to be connected

to C

. This set includes the terms in the conclu-

sion parts of valid association rules in M G B , whose

premise is C

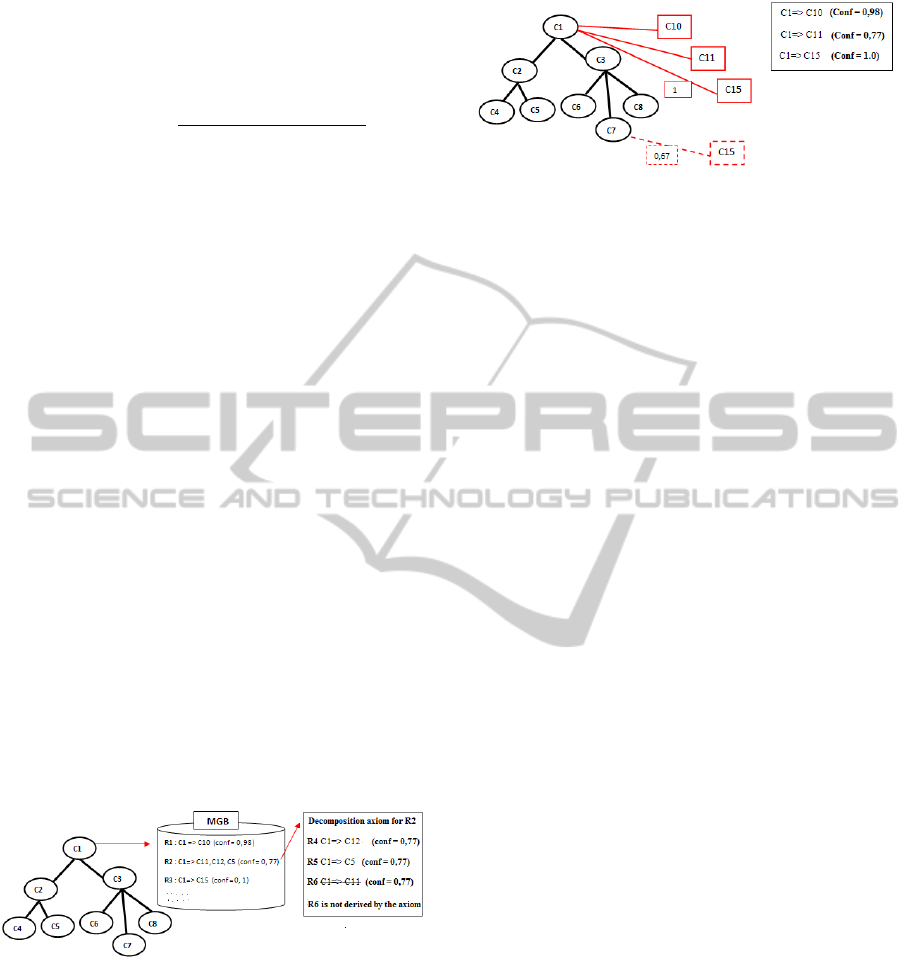
In the example depicted in Figure 2, the candidate

concepts for the enrichment related to the concept C

are {C

Figure 2: Example of detecting candidate concepts.

4.1.2 Step 2: Placement of New Concepts

In this step, we add the candidate concepts to the ini-

tial ontology O , while maintaining existing relations.

This allows to avoid adding redundant links in the

case of a concept candidate to be linked to several

concepts in the initial ontology O . In other words,

given a valid association rule R : C

⇒ C

in M G B ,

we select the candidate concept C

in the the associa-

tion rule R related to the initial concept C

∈ O where

Figure 3: Example of candidate concepts placement.

R has the greater conﬁdence among those in M G B

and having C

as premise.

The example depicted in Figure 3 illustrates the

placement of the new concepts C

et C

where con-

cept C

is removed since Con f(C

⇒ C

) = 1 is

greater than Conf(C

⇒ C

) = 0.67.

4.1.3 Step 3: Computing of C

Neighborhood

and Distance Measures

Among extracted terms as conclusions of valid asso-

ciation rules in M G B , there are some already known

terms, as they are already referenced as concepts by

the initial ontology O . In order to link only new terms

extracted with existing concepts, we proposeto deﬁne

the neighborhood of these concepts. Given a concept

in O , its neighborhood is deﬁned as follows:

Deﬁnition 5. Let C

be a concept, the neighborhood

of C

is the set of concepts in the ontology O

that can be accessed from C

by using the hierarchi-

cal link or by using one or more valid irredundant

associations rules in M G B .

The relations between a concept C

in O and its

neighborhood, ı.e., each candidate concept C

∈ N

are evaluated through a statistical measure called dis-

tance measure between C

and its neighborhood, de-

noted Dist

M G B

. It is calculated based on: (i) the

conﬁdence values of the association rules in M G B

selected for the ontology enrichment; and, (ii) simi-

larities between concepts in the original ontology O

assessed using Wu and Palmer’s similarity measure

(Wu and Palmer, 1994) (cf. Equation (7)).

In our enrichment approach, three conﬁgurations

are possible to evaluate the distance measure between

two concepts C

and C

in the enriched ontology

M G B

. For this, we present the following proposi-

tions.

Proposition 1. GivenC

a conceptof the initial ontol-

ogy O . If it exists a link between C

and a concept C

derived from an association rule in the generic basis

M G B , then:

Dist

M G B

) = Conf(R : C

⇒ C

) (8)

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

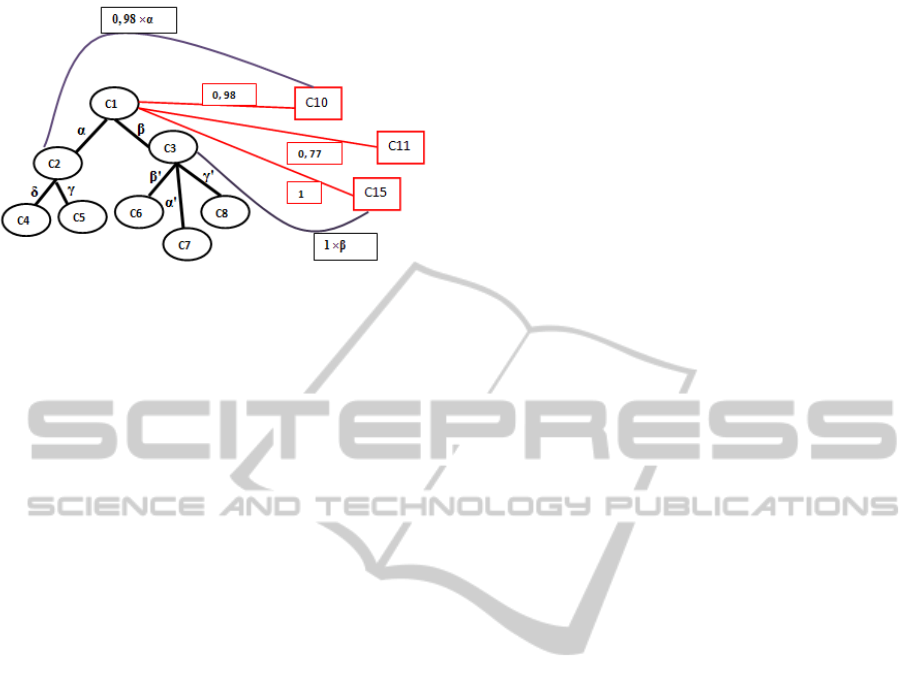
Figure 4: Examples of distance evaluation between con-

cepts in O

M G B

Proposition 2. If C

and C

belong to the initial on-

tology O then:

Dist

M G B

) = Sim

) (9)

Proposition 3. If C

is a concept added to the

enriched ontology O

M G B

and linked to C

where

Dist

M G B

) = Conf(R : C

⇒ C

) = β, then

each concept C

in O in relation with C

where

Sim

) = α, is also in relation with C

. In

this case, the distance measure is a mixte one and it

is calculated as follows:

Dist

M G B

) = α× β. (10)

Thereby, we consider that the neighborhood

N (C

) of a concept C

involves the set of k con-

cepts belonging to the conceptual proxemic network

M G B

, in relation with the concept C

, where the se-

mantic distance between them is greater than or equal

to a user-deﬁned θ. Formally, we have:

N (C

) = {C

| Dist

M G B

) ≥ θ, j ∈ [1..k]}

(11)

Example 9. The three conﬁgurations of the distance

measure evaluation are depicted in Figure 4, namely:

• Case 1 (Proposition 1): The concept C

is se-

lected from an association rule in M G B , so:

Dist

M G B

) = Conf(C

⇒ C

) = 0.98.

• Case 2 (Proposition 2): The two concepts C

and C

belong to the initial ontology O and

Dist

M G B

) = Sim

) = α.

• Case 3 (Proposition 3): A mixte distance is com-

puted betweenC

andC

sinceC

is linked toC

thanks to the valid association rule R :C

0.98

⇒ C

and an initial relation exits in O between C

and

, so: Dist

M G B

) = 0.98 × α

The generated result, i.e., the enriched ontology

M G B

, is thenexploredas a proxemicconceptuelnet-

work to represent the domain knowledge.

4.2 O

M G B

: A Proxemic Conceptuel

Network for Knowledge

Representation

In what follows, we describe an original proposal for

knowledge representation, namely a proxemic con-

ceptual network resulting from the enriched ontology

M G B

. The relationships between the concepts of

the conceptual network is quantiﬁed by the distance

measures introduced in Propositions 8, 9 and 10. The

originality of our proxemic conceptual network is its

completeness thanks to the combination, on the one

hand, of knowledge stemming from the initial ontol-

ogy, i.e., concepts and semantic relations, and, on the

other hand, implicit knowledge extracted as associa-

tion rules between terms.

Thus, a concept in our proxemic conceptual

network has three levels of semantic proximities,

namely:

1. A Referential Semantic: assignes to each con-

cept of O

M G B

an intensional reference, i.e., its

best concept sense through a disambiguation pro-

cess.

2. A Differential Semantic: associates to each con-

cept its neighbors concepts, i.e., those correlated

with it in the local context according to the Equa-

tion (11).

3. An Inferential Semantic: induced by irredun-

dant association rules between terms that asso-

ciate to each concept a inferential potential. In

our case, it will link the initial ontology concepts

to concepts contained in valid association rules

of M G B with respect to a minimum threshold

of conﬁdence mincon f and the proposed distance

measure.

Indeed, around each concept C

in O

M G B

, there is

a semantic proxemic subspace which represents the

different relations by computing distance measure

Dist

M G B

between its different neighbors concepts,

and between concepts and their extensions. This re-

sults an enriched knowledge representation.

In orderto prove that the proxemic conceptualnet-

work can have a great interest in IR and can con-

tribute to improve the retrieval effectiveness, we pro-

pose a document conceptual indexing approach based

on O

M G B

5 EVALUATION OF O

M G B

INFORMATION RETRIEVAL

Several ways of introducing additional knowledge

OntologyEnrichmentbasedonGenericBasisofAssociationRulesforConceptualDocumentIndexing

into Information Retrieval (IR) process have been

proposed in recent literature. In the last decade, on-

tologies have been widely used in IR to improve re-

trieval effectiveness (Vallet et al., 2005). Interest-

ingly enough, such ontology-based formalisms allow

a much more structured and sophisticated representa-

tion of knowledge than classical thesauri or taxonomy

(Andreasen et al., 2009). They represent knowledge

on the semantic level thanks to concepts and relations

instead of simple words.

Indeed, main contributions in document concep-

tual indexing issue are based on detecting new con-

cepts from ontologies and taxonomies and use them

to index documents instead of using simple lists of

words (Baziz et al., 2005; Andreasen et al., 2009;

Dinh and Tamine, 2011). Roughly, the indexing pro-

cess is performed in two steps, namely (i) ﬁrst detect-

ing terms in the document text by mapping document

representations to concepts in the ontology; then, (ii)

disambiguating the selected terms.

In the following, we introduce a novel concep-

tual documents indexing approach in IR, based on the

proxemic network O

M G B

which is the result of the

enrichment of an initial ontology O with the generic

basis M G B . Our strategy involves three steps de-

tailed below: (1) Identiﬁcation and weighting repre-

sentative concepts in the document through the con-

ceptual network O

M G B

; (2) Concepts disambiguation

using the enriched ontology; and, (3) Building the

document semantic kernel, denoted Doc-O

M G B

, by

selecting the best concepts-senses.

5.1 Identiﬁcation and Weighting of

Representative Concepts in the

Document

We assume that a document d is represented by a set

of terms, denoted by d = {t

, . . . , t

} and resulting

from the terms extraction stage. A term t

of a docu-

ment d, denoted t = {w

, . . . , w

} is composed of one

or more words and its length |t| is deﬁned as the num-

ber of words in t.

This step aims to identify and weight, for each in-

dex term of the document, the corresponding concept

in the proxemic conceptual proxemic O

M G B

. Thus,

the process of identiﬁcation and weighting of repre-

sentative concepts in a document d proceeds as fol-

lows:

1. Projection of the Document Index on O

M G B

It allows to identify mono-words or multi-words

concepts which correspond to index terms with re-

spect to their occurrence frequencies (Amirouche

et al., 2008). We select then the set of terms t

characterizing the document d, denoted by T(d),

namely:

T(d) = {(t

, f (t

)), . . ., (t

, f (t

))} such that t

∈ d,

(12)

where f(t

) means the occurrence frequency of t

in d.

2. Concepts Weighting. A widely used strategy in

IR for weighting terms is t f ×id f and its variants,

expressed as W(t, d) = t f(t) × id f(t, d) (Salton

and Buckely, 1988). Il this formula, t f represents

term frequency and id f is the inverse document

frequency. In (Baziz et al., 2005), authors pro-

posed, for the case of multi-word terms, a statisti-

cal weighting method named c f × id f and based

both on classical t f × id f measure and the length

of the terms. So, for an extracted concept t com-

posed of n words, its frequency in a document d is

equal to the number of occurrences of the concept

itself t, and the one of all its sub-concepts. The

frequency is calculated as follows (Baziz et al.,

2005):

cf(t) = f(t) +

∑

∈sub(t)

(

|t|

× f(t

)) (13)

where sub(x) is the set of all possible sub-sets

which can be derived from a term x, |x| represents

the number of words in x and f(t) is the occur-

rence frequency of t in d.

In this step of our conceptual indexing process,

concepts weighting assignes to each concept a

weight that reﬂects its importance and represen-

tativity in a document. We propose a new weight-

ing measure which considers both statistical and

semantic representativities of concepts in a given

document.

The key feature of the weighting way that we pro-

pose is to consider for a term t, in addition to its

weight given by cf(t) × id f (t, d), the weights of

concepts C

belonging to its neighborhood.

Hence, the statistical representativity, denoted

Stat

, is computed by using Equation (13),

namely:

Stat

(t, d) = c f(t) × id f(t, d) (14)

Moreover, while considering the proxemic con-

ceptuel network O

M G B

, we propose that the se-

mantic representativity of a term t in a document

d, denoted W

Sem

(t, d), takes into account the dif-

ferent links in O

M G B

between each occurrence of

t and other concepts in its neighborhood. This se-

mantic representativity is computed by using the

semantic distance measure Dist

M G B

as deﬁned in

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

Propositions 1, 2 and 3, between each occurrence

of a term t in O

M G B

and the concepts in its

neighborhood N (C

). It is computed as follows:

Sem

(t, d) =

∑

∈S

∑

∈N (C

)

Dist

M G B

) × f(C

)

(15)

such that S

= {C

, . . . ,C

} is the set of all con-

cepts linked to the term t, i.e., occurrences of t.

The underlying idea is that the global representa-

tivity of a term t in a document d, i.e., its weight,

further denoted W

Doc

, is formulated as the combi-

nation between the statistical representativity and

the semantic one, and is computed as:

Doc

(t, d) = W

Stat

(t, d) +W

Sem

(t, d) (16)

The document index, denoted Index(D), is then

generated by selecting only terms whose global

representativity, i.e., W

Doc

(t, D), is greater than or

equal to a minimal representativity threshold.

5.2 Concepts Disambiguation

We assume that each term t

in a document d can

have multiple senses, denoted by S

= {C

,...,C

} and

are represented by corresponding concepts in O

M G B

Thus, a term t

∈ Index(d) has |S

|=n senses, i.e., it

represents n concepts in O

M G B

Given a term t in the document index Index(d) =

, . . . ,t

}, the disambiguation aims to identify and

to assign it the appropriate sense with respect to its

context. We proposein the following an O

M G B

-based

disambiguation approach. In this regard, we consider

that each index term in Index(d) contributes to the se-

mantic representation of d with only one sense even if

a term can have different senses in the same document

(Amiroucheet al., 2008). Hence, disambiguation task

consists to select for each index term in Index(d), its

best sense in d, with respect to a computed score for

each concept-sense in O

M G B

In the literature, various methods and metrics have

been proposed for disambiguatingwords in text (Nav-

igli, 2009). In our case, we got inspired by the ap-

proach described in (Baziz et al., 2005)whichis based

on the computation of a score for every concept-sense

linked to an index term and using WordNet ontology.

Our disambiguation approach differs from that

one proposed in (Baziz et al., 2005) in the way of

calculating the score. Indeed, we believe that only

considering the semantic proximity between concepts

is insufﬁcient to detect the best sense of a term. In

(Baziz et al., 2005), the authors do not take into ac-

count the representativity of the terms in the docu-

ment context. Besides, they do notconsider local con-

text of the word in the document, i.e., the correlation

of the senses of neighbors terms, and in the concept

hierarchy.

To overcome these limits, we suggest that the best

sense to be assigned to a term t

in the document

d shall be strongly correlated with other elements,

namely:

1. The local context of the term t

in the document d:

This means that the disambiguation of t

considers

its neighbors terms in the document d. We deﬁne

the local context of a term t

as follows:

Deﬁnition 6. The local context of a term t

in a

document d, denoted Context

), is a termset in

T(d) belonging to the same sentence where ap-

pears t

2. The context of each sense in O

M G B

: The disam-

biguation of a concept C

considers its neighbor-

hood, i.e., N

3. Term representativity in the document context:

The best sense for a term t

in d is that which is

highly correlated with the most important sense

in d. To do this, we integrate the term weight

in the document, i.e., its global representativity,

computed w.r.t Equation (16).

In our disambiguation approach, we ﬁrstly deﬁne

the weight of a concept-senseC

in S

as the weight of

its associated index term t

. That is, for a term t

, the

score of its j

sense, denoted by C

, is computed as:

C Score(C

) =

∑

∈N (C

)∪C

∑

∈Context

),l6=i

Score

Doc

)×Dist(C

)

(17)

where:

Score

Doc

) = W

Doc

, d) ×W

Doc

, d) (18)

and

Dist(C

) =

∑

k∈[1..n

]

Dist

M G B

) (19)

such that n

represents the number of senses in

M G B

which is proper to each term t

, W

Doc

, d) and

Doc

, d) are the weights associated tot

and t

in the

document d.

The concept-sense C

which maximizes the score

C Score(C

) is then retained as the best sense of the

term t

. Formally, we have:

argmax

j ∈ [1..n

]

{C Score(C

)} (20)

Indeed, by performing the different formulas (17),

(18), (19) and (20), we have disambiguated the con-

ceptC

which will be a node in the proxemic semantic

network of the document d.

OntologyEnrichmentbasedonGenericBasisofAssociationRulesforConceptualDocumentIndexing

5.3 Building the Proxemic Semantic

Network Doc-O

M G B

The last step of our document conceptual indexing

process is the building of the the proxemic network

representing a document content, denoted in the se-

quel Doc-O

M G B

. To do so, we select its nodes, i.e.,

concept senses, by computing for each of them the

best score C Score. The nodes of Doc-O

M G B

are

initialized with the selected concepts in the disam-

biguation step. Then, each concept of Doc-O

M G B

declined in more intensions and extensions thanks to

the structure of O

M G B

, which are themselves linked

to other concepts of the generic basis of association

rules M G B .

Thus, around each node in Doc-O

M G B

gravitates

a three-dimensional proxemic ﬁeld synthesizing three

types of semantic, namely the referential semantic,

the differential semantic and the inferential one as ex-

plained in Sub-section 4.2.

Therefore, thanks to the obtained structure, i.e.,

Doc-O

M G B

, we move from a simple index containing

single index terms to a proxemic three-dimensional

indexing space. The expected advantage on this novel

document representation is to get a richer and more

precise meaning representation in order to obtain a

more powerful identiﬁcation of relevant documents

matching the query in an IR system.

6 EXPERIMENTAL EVALUATION

In order to evaluate our ontology enrichment ap-

proach based on the generic basis M G B , we propose

to incorporatethe generated conceptualproxemic net-

work Doc-O

M G B

into a conceptual document index-

ing framework. For this purpose, we consider the well

known medical ontology MeSH as domain ontology

(D´ıaz-Galiano et al., 2008). Indeed, in MeSH, each

concept is described by a main heading (preferred

term), one or many concept entries (non-preferred

terms), qualiﬁers, scope notes, etc. Thus, we used

main headings and qualiﬁers as indexing features in

our evaluation.

6.1 Test Collection

We used the OHSUMED test collection, which is a

MEDLINE sub-collection used for biomedical IR in

TREC9 ﬁltering Track, under the Terrier IR platform

(http://terrier.org/). Each document has been anno-

tated by human experts with a set of MeSH concepts

revealingthe subject matter(s) of the document. Some

statistical characteristics of the OHSUMED collec-

tion are depicted in Table 2.

Table 2: OHSUMED test collection statistics.

Number of documents 348, 566

Average document length 100 tokens

Number of queries 63

Average query length 12 terms

Average number of relevant docs/query 50

6.2 Experimental Setup

For measuring the IR effectiveness, we used exact

precision measures P@10 and P@20, representing re-

spectively the mean precision values at the top 10

and 20 returned documents, and MAP representing

the Mean Average Precision computed over all top-

ics. The purpose of our experimental evaluation is to

determine the utility of our ontology enrichment ap-

proach on the MeSH ontology using irredundant as-

sociation rules between terms which are derived from

the document collection OHSUMED. Hence, we pro-

pose to assess the impact of exploiting the conceptual

proxemic network O

M G B

in document indexing on

the retrieval effectiveness.

Therefore, we carried out two series of exper-

iments applied on the articles titles and abstracts.

The ﬁrst one is based on the classical document in-

dexing using the state-of-the-art weighting scheme

OKAPI BM25 (Jones et al., 2000), as the baseline, de-

noted BM25. The second one concerns our concep-

tual indexing approach and consists of four scenarios,

namely:

1. The ﬁrst one concerns the document expansion

using concepts manually assigned by human ex-

perts, denoted I

Expert

2. The second one concerns the document expansion

using only preferred concepts of the MeSH ontol-

ogy before any enrichment, denoted I

MeSH

3. The third one concerns the document expansion

based on additional terms derived from valid as-

sociation rules of the M G B generated from the

document collection OHSUMED, denoted I

M G B

Notice that we set up minimal support thresh-

old minsupp and minimal conﬁdence threshold

minconf, respectively to, 0.05 and 0.3.

4. The last one concerns the documentexpansion us-

ing concepts identiﬁed from the proxemic con-

ceptual network Doc-O M G B , denoted I

G B

which is the result of the MeSH enrichment with

the generic basis of irredundant association rules

M G B derived from OHSUMED collection.

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

6.3 Results and Discussion

We now present the experimental results of the pro-

posed document indexing strategies. We assess the

IR effectiveness using the extracted concepts and our

proposed disambiguation approach.

Table 3 depicts the IR effectiveness of the I

Expert

MeSH

and our two semantic indexing approaches

based on the generic basis of association rules M G B

and the proxemic conceptuel network O

M G B

. We ob-

serve that in an automatic setting, our best indexing

method, namely I

M G B

, provides the highest improve-

ment rate (+17.57%) while the M G B based method

only gives+4.17% in terms of MAP over the baseline

BM25. This proves the interest to take into account

both terms from association rules and the concepts

selected from enriched ontology during the concept

extraction process. Results highlight that using only

concepts extracted from the MeSH ontology lead to

a small improvement of IR effectiveness in the case

of document indexing. Furthermore, we see that the

Expert

, I

M G B

and I

M G B

methods consistently outper-

form the baseline BM25.

Although the gain of the I

M G B

method is smaller

than the I

Expert

method, which represents the best sce-

nario, in terms of MAP (23.33% vs. 17.57%) (cf.

Table 3), the former yields improvement in terms of

P@10 and P@20, which is less signiﬁcant in the other

methods, namely I

MeSH

and I

M G B

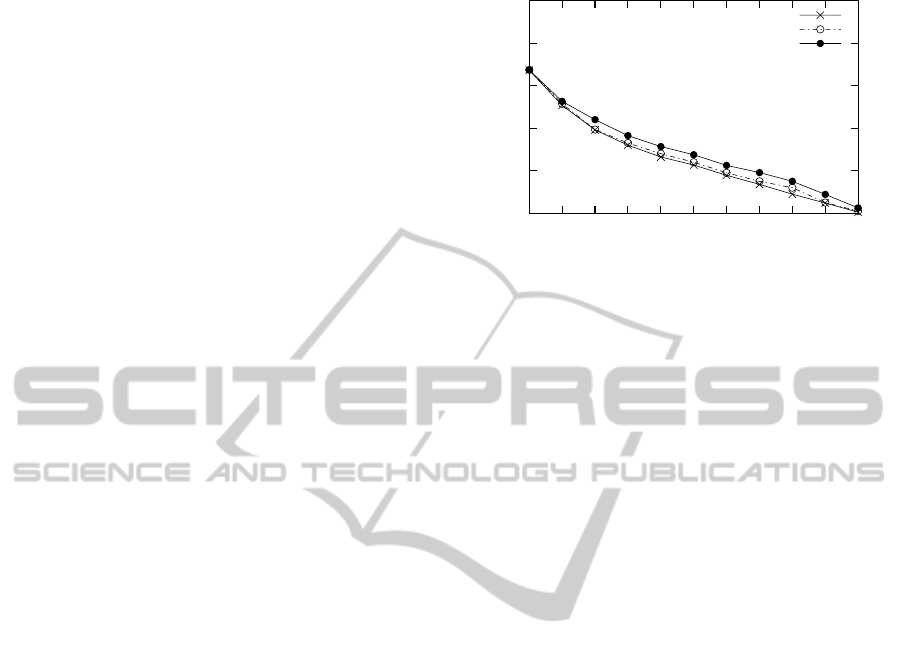
Figure 5 sheds light on the advantage of the in-

sight gained through the M G B irredundant asso-

ciation rules and the conceptual proxemic network

M G B

in the context of conceptual document index-

ing. We note that the increase of the precision at 11

points of recall with the I

M G B

method is not so im-

portant with respect to the baseline BM25. This can

be explained by the fact that OHSUMED is a scien-

tiﬁc medical collection where terms have very weak

distributions and marginally co-occur. Moreover, an

important part of the vocabulary is not used, since

it is not correctly analyzed, due to the used tagger

which does not identify speciﬁc and scientiﬁc terms

of OHSUMED. Moreover, we notice in our experi-

ments that the improvement of the average precision

is less signiﬁcant for high support values. Indeed, ex-

tracting association rules, when considering a high

support value, leads to some trivial associations be-

tween terms that are very frequent in the document

collection.

In orderto show how our indexing approachbased

on the conceptual proxemic network O

M G B

is statis-

tically signiﬁcant, we perform the Wilcoxon signed

rank test (Smucker et al., 2007) between means of

each ranking obtained by our indexing method and

0.2

0.4

0.6

0.8

0 10 20 30 40 50 60 70 80 90 100

Precision

Recall (%)

OHSUMED collection

Baseline (BM25)

Index based MGB

Index based OMGB

Figure 5: Precision-recall curves corresponding to the base-

line vs index based on M G B and O

M G B

the baseline BM25. The reason for choosing the

Wilcoxon signed rank test is that it is more powerful

and indicative test as it considers the relative magni-

tude in addition to the direction of the differences con-

sidered. Experimental results for a signiﬁcance level

α = 1%, show with the paired-sample Wilcoxon-test,

that our based O

M G B

document indexing approach is

statistically signiﬁcant (p-value < 0.01%) compared

to the baseline BM25. Thus, we conclude that con-

ceptual indexing by an enriched ontology with irre-

dundant association rules between terms, would sig-

niﬁcantly improve the biomedical IR performance.

7 CONCLUSIONS

The work developedin this paper lies within the scope

of domain ontologies enrichment and their applica-

tion in IR ﬁeld. We have introduced an automatic

enrichment approach based on a generic basis of as-

sociation rules between terms (Latiri et al., 2012) to

identify additional concepts linked to ontology con-

cepts. Interestingly enough, these association rules

are extracted from the target document collection by

means of mining mechanisms which in turn rely on

results from FCA ﬁeld (Ganter and Wille, 1999). The

placement of new concepts is carried out through the

deﬁned distance measures and the neighborhood con-

cept. The result is a proxemic conceptual network

where nodes represent disambiguated concepts and

edges are materialized by the value of distance mea-

sure between concepts. Threesemantic relations from

this network are used, namely: a referential semantic,

a differential semantic and an inferential semantic. To

evaluate the contribution of the conceptual proxemic

network in the retrieval effectiveness, we integrate it

in a conceptual document indexing. In this regard, the

conducted experiments using OHSUMED collection

OntologyEnrichmentbasedonGenericBasisofAssociationRulesforConceptualDocumentIndexing

Table 3: IR effectiveness (% change) over 63 queries.

Strategies MAP P@10 P@20

Baseline (BM25) 23.96 41.9 35.00

Expert

29.55 (+23.33) 45.08 (+7.59) 39.92 (+14.06)

MeSH

24.73 (+3.21) 41.27 (-1.50) 35.87 (+2.49)

M G B

24.96 (+4.17) 42.77(+2.08) 36.08 (+3.09)

M G B

28.17 (+17.57) 44.33 (+5.80) 38.17 (+10.86)

and MeSH ontology which highlighted an improve-

ment in the performances of the information retrieval

system, in terms of both recall and precision metrics.

As work in progress, we focus on enrichment of mul-

tilingual ontologies by means of inter-lingual associ-

ation rules between terms introduced in (Latiri et al.,

2010).

ACKNOWLEDGEMENTS

This work was partially supported by the French-

Tunisian project CMCU-UTIQUE 11G1417.

REFERENCES

Agrawal, R. and Skirant, R. (1994). Fast algorithms for

mining association rules. In Proceedings of the 20

International Conference on Very Large Databases

(VLDB 1994), pages 478–499, Santiago, Chile.

Amirouche, F. B., Boughanem, M., and Tamine, L. (2008).

Exploiting association rules and ontology for semantic

document indexing. In Proceedings of the 12

Inter-

national Conference on Information Processing and

Management of Uncertainty in Knowledge-based Sys-

tems (IPMU’08), pages 464–472, Malaga, Espagne.

Andreasen, T., Bulskov, H., Jensen, P., and Lassen, T.

(2009). Conceptual indexing of text using ontologies

and lexical resources. In Proccedings of the 8

In-

ternational Conference on Flexible Query Answering

Systems, FQAS 2009, volume 5822 of LNCS, pages

323–332, Roskilde, Denmark. Springer.

Balc´azar, J. L. (2010). Redundancy, deduction schemes,

and minimum-size bases for association rules. Logical

Methods in Computer Science, 6(2):1–33.

Bastide, Y., Pasquier, N., Taouil, R., Stumme, G., and

Lakhal, L. (2000). Mining minimal non-redundant as-

sociation rules using frequent closed itemsets. In Pro-

ceedings of the 1

International Conference on Com-

putational Logic, volume 1861 of LNAI, pages 972–

986, London, UK. Springer.

Baziz, M., Boughanem, M., Aussenac-Gilles, N., and

Chrisment, C. (2005). Semantic cores for represent-

ing documents in IR. In Proceedings of the 2005 ACM

Symposium on Applied Computing, SAC’05, pages

1011–1017, New York, USA. ACM Press.

Ben Yahia, S., Gasmi, G., and Nguifo, E. M. (2009). A

new generic basis of factual and implicative associa-

tion rules. Intelligent Data Analysis, 13(4):633–656.

Bendaoud, R., Napoli, A., and Toussaint, Y. (2008). Formal

concept analysis: A uniﬁed framework for building

and reﬁning ontologies. In Proceedings of 16

Inter-

national Conference on the Knowledge Engineering:

Practice and Patterns (EKAW 2008), volume 5268 of

LNCS, pages 156–171, Acitrezza, Italy. Springer.

Benz, D., Hotho, A., and Stumme, G. (2010). Semantics

made by you and me: Self-emerging ontologies can

capture the diversity of shared knowledge. In Pro-

ceedings of the 2

Web Science Conference (Web-

Sci10), Raleigh, NC, USA.

Cimiano, P., Hotho, A., Stumme, G., and Tane, J. (2004).

Conceptual knowledge processing with formal con-

cept analysis and ontologies. In Proceedings of the

second International Conference on Formal Concept

Analysis, ICFCA 2004, pages 189–207, Sydney, Aus-

tralia.

Di-Jorio, L., Bringay, S., Fiot, C., Laurent, A., and Teis-

seire, M. (2008). Sequential patterns for maintaining

ontologies over time. In Proceedings of the Interna-

tional Conference On the Move to Meaningful Inter-

net Systems, OTM 2008, volume 5332 of LNCS, pages

1385–1403, Monterrey, Mexico. Springer.

D´ıaz-Galiano, M. C., Garc´ıa-Cumbreras, M. A., Mart´ın-

Valdivia, M. T., Montejo-R´aez, A., and na L´opez, L.

A. U. (2008). Integrating MeSH Ontology to Improve

Medical Information Retrieval. In Proceedings of the

Workshop of the Cross-Language Evaluation Fo-

rum, CLEF 2007, Advances in Multilingual and Mul-

timodal Information Retrieval, volume 5152 of LNCS,

pages 601–606, Budapest, Hungary. Springer.

Dinh, D. and Tamine, L. (2011). Combining global and lo-

cal semantic contexts for improving biomedical infor-

mation retrieval. In Proceedings of the 33

European

Conference on IR Research, ECIR 2011, volume 6611

of LNCS, pages 375–386, Dublin, Ireland. Springer.

Faatz, A. and Steinmetz, R. (2002). Ontology enrichment

with texts from the www. In Proceedings of the

ECML/PKDD-Workshop on Semantic Web Min-

ing, pages 20–34, Helsinki, Finland.

Ganter, B. and Wille, R. (1999). Formal Concept Analysis.

Springer.

Jones, K. S., Walker, S., and Robertson, S. E. (2000). A

probabilistic model of information retrieval: develop-

ment and comparative experiments. Information Pro-

cessing and Management, 36(6):779–840.

Latiri, C., Haddad, H., and Hamrouni, T. (2012). To-

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

wards an effective automatic query expansion pro-

cess using an association rule mining approach. Jour-

nal of Intelligent Information Systems, pages DOI:

10.1007/s10844–011–0189–9.

Latiri, C., Smali, K., Lavecchia, C., and Langlois, D.

(2010). Mining monolingual and bilingual corpora.

Intelligent Data Analysis, 14(6):663–682.

Maedche, A., Pekar, V., and Staab, S. (2002). Ontology

Learning Part One - On Discovering Taxonomic Re-

lations from the Web, pages 301–322. Springer.

Navigli, R. (2009). Word sense disambiguation: A survey.

ACM Comput. Surv., 41:1–69.

Navigli, R. and Velardi, P. (2006). Ontology enrich-

ment through automatic semantic annotation of on-

line glossaries. In Proceedings of 15

International

Conference, EKAW 2006, Podebrady, Czech Republic,

volume 4248 of LNCS, pages 126–140. Springer.

Neshatian, K. and Hejazi, M. R. (2004). Text categoriza-

tion and classiﬁcation in terms of multiattribute con-

cepts for enriching existing ontologies. In Proceed-

ings of the 2

Workshop on Information Technology

and its Disciplines, WITID’04, pages 43–48, Kish Is-

land, Iran.

Parekh, V., Gwo, J., and Finin, T. W. (2004). Mining do-

main speciﬁc texts and glossaries to evaluate and en-

rich domain ontologies. In Proceedings of the In-

ternational Conference on Information and Knowl-

edge Engineering, IKE’04, pages 533–540, Las Ve-

gas, Nevada, USA. CSREA Press.

Salton, G. and Buckely, C. (1988). Term-weighting ap-

proaches in automatic text retrieval. Information Pro-

cessing and Management, 24(5):513–523.

Smucker, M. D., Allan, J., and Carterette, B. (2007). A

comparison of statistical signiﬁcance tests for infor-

mation retrieval evaluation. In Proceedings of the 16

International Conference on Information and Knowl-

edge Management, CIKM 2007, pages 623–632, Lis-

boa, Portugal. ACM Press,.

Song, M., Song, I., Hu, X., and Allen, R. B. (2007). Integra-

tion of association rules and ontologies for semantic

query expansion. Data and Knowledge Engineering,

63(1):63 – 75.

Stumme, G., Taouil, R., Bastide, Y., Pasquier, N., and

Lakhal, L. (2002). Computing Iceberg Concept Lat-

tices with Titanic. Journal on Knowledge and Data

Engineering, 2(42):189–222.

Valarakos, A., Paliouras, G., Karkaletsis, V., and Vouros,

G. (2004). A name-matching algorithm for sup-

porting ontology enrichment. In Vouros, G. and

Panayiotopoulos, T., editors, Methods and Applica-

tions of Artiﬁcial Intelligence, volume 3025 of LNCS,

pages 381–389. Springer.

Vallet, D., Fernndez, M., and Castells, P. (2005). An

ontology-based information retrieval model. In The

Semantic Web: Research and Applications, volume

3532 of LNCS, pages 103–110. Springer.

Wu, Z. and Palmer, M. (1994). Verb semantics and lexical

selection. In Proceedings of the 32

annual meet-

ing of the Association for Computational Linguistics,

pages 133–138, New Mexico, USA.

Zaki, M. J. (2004). Mining non-redundant association rules.

Data Mining and Knowledge Discovery, 9(3):223–

248.

OntologyEnrichmentbasedonGenericBasisofAssociationRulesforConceptualDocumentIndexing