User based Collaborative Filtering with Temporal Information for

Purchase Data

Maunendra Sankar Desarkar and Sudeshna Sarkar

Department of CSE, Indian Institute of Technology Kharagpur, Kharagpur, India

Keywords:

Item Recommendation, Collaborative Filtering, Temporal Recommendation.

Abstract:

User based collaborative ﬁltering algorithms are widely used for generating recommendations for users. Stan-

dard user based collaborative ﬁltering algorithms do not consider time as a factor while measuring the user

similarities and building the recommendation list. However, users’ interests often shift with time. Recom-

mender systems should therefore rely on recent purchases of the users to address this user dynamics. Items

also have their own dynamics. Most of the items in a recommender system are widely popular just after their

releases butdo not sell that well afterwards. Giving more importance to the recent purchases of the experts may

capture the item dynamics and hence result in better recommendation accuracy. We study the performances

of different time-aware user based collaborative ﬁltering algorithms on several benchmark datasets. The pro-

posed algorithms use the time-of-purchase information for calculating user similarities. The time information

is also used while combining the purchase behaviors of the experts and generating the ﬁnal recommendation.

1 INTRODUCTION

In the recommendation problem, given a set of pur-

chase records from different users, the task is to ﬁnd

a list of recommended or suggested items for the

users. This list of items would be different for dif-

ferent users, as each user has his/her own personal

choices of the items.

Users’ purchase patterns for different products

are different. For systems where a user may pur-

chase/access the same item multiple times (e.g.

music/video/article hosting systems, stores selling

household items), past purchases by a user can be

used as a basis for future recommendation. On the

other hand, there are systems where the user gener-

ally does not purchase the same item more than once.

Examples include purchases of books, music CDs,

Movie DVDs etc. In such cases, the system can con-

sider purchases or accesses made by users with sim-

ilar purchase or access behaviors. User based col-

laborative ﬁltering algorithms that use this concept of

similar tastes of users can be used for recommending

items for purchase stores where the same user does

not purchase the same item more than once.

Traditional user based collaborative ﬁltering algo-

rithms do not consider time as a factor while ﬁnding

similar users and generating the recommendation list.

The basic user based collaborative ﬁltering frame-

work may not work well if the interest proﬁle of the

user changes with time. In reality, users’ interests of-

ten shift over time. If the algorithm looks at the entire

purchase history of the user, and gives equal impor-

tance to all the items purchased in the past, the rec-

ommended list may include items that are much sim-

ilar to the ones the user liked in the past. Chances

are that the user will not like those items as his inter-

est has now shifted to different types of items. Such

situations may be addressed by focusing more on the

recent purchases of the users.

The items also have their own dynamics. Many

items are popular in a narrow time window after their

release. As the time progresses, their purchases de-

crease, and after some time, the item is not purchased

much. The length of this window (which we call pop-

ularity span) may vary from item to item. We looked

at the popularity spans of different items from sevaral

real world datasets. It was observed that, for all the

datasets, the popularity of majority of the items decay

with time. Figure 1 shows the popularity span his-

togram for sample datasets from Amazon and Netﬂix.

One can use the information regarding the current

selling trend of the items while generating the recom-

mendations. If an item is currently popular, the item

can be recommended to many users. However, if a

system recommends items by looking at the popular-

ity value only, then the recommendation will lose the

Desarkar M. and Sarkar S..

User based Collaborative Filtering with Temporal Information for Purchase Data.

DOI: 10.5220/0004134400550064

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2012), pages 55-64

ISBN: 978-989-8565-29-7

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

0.1

0.2

0.3

0.4

0.5

0.6

0.7

10 20 30 40 50 60 70 80 90 100 110 120

(a) Item popularity span histogram for Amazon Music dataset

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

10 20 30 40 50 60 70 80 90 100 110 120

(b) Item popularity span histogram for Amazon DVD dataset

0.1

0.2

0.3

0.4

0.5

0.6

10 20 30 40 50 60 70 80 90 100 110 120

0.05

0.1

0.15

0.2

0.25

0.3

0.35

10 20 30 40 50 60 70 80 90 100 110 120

(d) Item popularity span histogram for Netﬂix dataset

Figure 1: Item popularity span histograms for different datasets. For each dataset, we considered the items that were purchased

at least 20 times. If the popularity score of an item i in month m is at least 20, then we say that the product was popular in

month m. The largest popularity span of an item is the largest time window (in months) in which the item was popular. Each

graph represents the histogram of the largest popularity span for different items in a particular dataset. Y-axis shows the

fraction of items that fall in a particular bin of the histogram.

personalization aspect. The system may recommend

an item just because it is popular,but the user may not

have any interest in that item. On the other hand, for a

target user u, if an item is popular among many of the

users who have interests similar to that of u, then the

item might be of interest to u also. We try to incorpo-

rate the item dynamics in the user based collaborative

ﬁltering framework by looking at the recent purchases

of the similar users or experts.

In this work, we explore several time-aware user

based collaborativeﬁltering algorithms for the recom-

mendation problem on purchase data. We perform

experimentation on Amazon and Netﬂix datasets and

analyze the performances of the algorithms. We con-

duct experiments in a framework where the recom-

mendation algorithms are run just prior to each pur-

chase made by the user, and we see if the system is

able to include the next purchase in its recommen-

dation list. Experimental results indicate that recom-

mendation performance can be improved by giving

more importance to the recent purchases of both the

user and the experts.

2 RELATED WORK

There has been some research work on designing

time-aware collaborative ﬁltering algorithms for solv-

ing the recommendation problem. (Kawamae et al.,

2009) considers precedence information at user level

and uses it for recommendation generation. A user

who not only purchases many of the items that the

target user also purchases, but also makes those pur-

chases before the target user can be used as an expert

for recommending items to the target user. It also con-

siders other time speciﬁc factors such as launch time

of items in the recommendation model. In (Lee et al.,

KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

2008), the authors proposed an algorithm that con-

verts a purchase to an implicit rating by considering

the launch-time of the item and the time of the pur-

chase. This implicit rating is then used in collabora-

tive ﬁltering framework for recommendation. A rec-

ommender system based on tag and time information

for social tagging systems is presented in (Zheng and

Li, 2011). It uses a combination of a tag-weight ma-

trix and a time-weight matrix for this purpose. For

each user-tag pair, the tag-weight matrix stores the

fraction of times the user has used the tag. The time-

weight matrix, for a user-tag pair, stores a value that is

dependent on the time when the user entered the tag.

Temporal algorithms have also been used for solv-

ing various other types of recommendation problems.

In (Parameswaran et al., 2010), the authors propose a

precedence mining model that estimates the probabil-

ity of future consumption based on temporal patterns.

The algorithm is used for a course recommendation

application where depending on the past courses that

a student has taken new courses are suggested to the

student. There are algorithms that study temporal-

ity where there is a strict order or path followed by

the user, and the goal is to predict the next step in

that sequence. A typical example of such a task is

the next-page prediction problem in which the system

tries to predict the next web page a user will access

given a sequence of pages visited up to now ((Desh-

pande and Karypis, 2004)). In (Shani et al., 2005),

purchase sequences are viewed as states of a dynamic

system. If one sequence leads to another sequence,

then the system is considered to have made a transi-

tion to the new state. This state transition model is

described as a Markov Decision Process and is used

to generate recommendations. Algorithms based on

precedence mining may not be appropriate for solving

the recommendation problem in a more general case

where such precedence information are not much use-

ful. Two users who purchase the same set of products,

but in different order, may have similar tastes of the

items. One of these users can be used for generating

recommendations for the other. (Rendle et al., 2010)

uses a matrix factorization technique over personal-

ized Markov chains representing sequential purchase

patterns of users. This method called FPMC (Fac-

torizing Personalized Markov Chains) is used for the

next basket recommendation problem. The method

assumes that a user may purchase the same item mul-

tiple times.

A related problem where time aware algorithms

have also been used is the rating prediction problem.

Rating prediction problem is used in systems where

users give ratings to different items. In (Ding and

Li, 2005; Ding et al., 2006), the authors assign time

weights for items so that the recently rated items are

able to contribute more to the prediction. (Campos

et al., 2010) calculates the most similar users with all

the available information from the dataset. After that,

only the most recent ratings of the neighbors are used

to ﬁnd the predicted rating. (Koren, 2008) merges the

factor and neighborhood models for collaborative ﬁl-

tering to solve the task of rating prediction. A factor

model that looks at several temporal aspects from rat-

ing data is discussed in (Koren, 2009).

A combination of bias model and time weighted

similarity model is presented in (Rongfei et al., 2010).

3 PRELIMINARIES AND

PROBLEM DEFINITION

Let U and I be the set of users and items respectively.

Let D be a collection of past purchase records. Each

record in D is called a purchase or a transaction, and

is of the form (u,i,t

) which represents the fact that

user u has purchased item i at time t

Given a target user u ∈ U and past purchase data

D, the goal of a recommender system is to ﬁnd a set

⊆ I of items that the target user may want to pur-

chase in future.

4 OUR ALGORITHMS

For the systems where the same users generally do

not purchase the same items multiple times, the user

based collaborativeﬁltering frameworkis widely used

for generating the recommendations. Algorithms us-

ing this framework work in two phases: expert selec-

tion and recommendation generation. As discussed in

Section 1, giving importance to the recent purchases

of the user in the expert selection phase may address

the issues related to the users’ interest shift. Giving

more importance to the recent purchases of the ex-

perts may capture the item dynamics. For both the

target user and the experts, the system can look at

their purchase histories in three different ways: (a)

treat all items as equal, (b) consider items purchased

in a small time window, or (c) look at the entire his-

tory but with discounted importance assigned to the

items purchased long back. We explore four out of

these nine different combinations and present those

algorithms in this section.

4.1 Algorithm 1: Count (CNT)

The ﬁrst among these four algorithms does not look

at time information. We call this algorithm as Count,

UserbasedCollaborativeFilteringwithTemporalInformationforPurchaseData

or CNT in short. We use this algorithm as the base-

line. We estimate the Similarity weight of a user v for

a target user u as the number of items that both u and

v have purchased

. The top-K users according to the

similarity weights are selected as the experts. In the

second phase, the algorithm looks at the purchase his-

tories of the experts. For each item, its score is given

by the number of experts who have purchased it. The

items are then sorted in non-increasing order of their

scores, and the top N items are recommended to u.

4.2 Algorithm 2: Recent-k (RECK)

CNT looks at all the purchases made by the users in

the past and treats them equally. However, users’ in-

terests often shift over time. To handle this situation,

we do not look at the entire history of the target user’s

purchases. Our next algorithm RECK looks at a small

window (say, of size k) of his/her recent purchases.

Experts are selected based on how many of the items

from this window they have bought.

Let the set of the k most recent purchases of user

u be I

. The expert selection and recommendation

generation phases are performed as follows:

• For each user v ∈ U \ i, ﬁnd weight w

|. Select top-K experts according to sim-

ilarity weights. Let this set be E.

• For each item i /∈ I

, score s

∑

v∈E∧i∈I

. Rec-

ommend top-N items with the highest scores.

4.3 Algorithm 3: Recent-k with Weight

(RECKW)

The next algorithm, represented by RECKW, extends

RECK by adding more time-dependent factors in the

expert selection and recommendation generation pro-

cesses. RECK looks at only the most recent purchases

of the target user to ﬁnd the experts. In RECK, if v

purchased many items that the target user u has pur-

chased recently, then v gets high similarity weight for

u. However, all those purchases of v might be made

long back. If this user v is selected as an expert,

and v’s interest has shifted recently, then the system

may end up recommending many items that v has pur-

chased recently, but those items do not match u’s re-

cent taste. This observation motivated us to look at v’s

recent interest, and give more weight to v if his/her re-

cent purchases are similar to u’s recent purchases. To

calculate the item’s contribution to the user’s similar-

ity weight, we take help of a decay function that we

denote by decay(t). There are two properties that the

Please note that the it is not necessary to normalize the

similarity weights in a ﬁxed range.

function should have: (a) It should be monotonically

decreasing, and (b) for very large values oft, the value

of the function should be small but non-zero. The ﬁrst

property ensures that recent purchases are more im-

portant than old purchases. The second property sig-

niﬁes that very old purchases are not completely ig-

nored, but they have much lesser importance weight

compared to recent purchases. We use the following

decay function in our algorithms.

decay(t) =

+ λ

1+ λ

. (1)

γ and λ are constants and assume values from the

continuous interval [0,1]. It can be easily veriﬁed that

the function is monotonically decreasing. Also, for

very large t, the value of the function is

1+λ

, which is

non zero. This value can be controlled by choosing a

value of λ that is suitable for the application. Hence,

the function satisﬁes the above properties. Please note

that there are several different choices of decay func-

tions. However, our focus in this work is to show that

recommendation performances can be improved by

giving more importance on the users’ and the experts’

recent purchases. So we chose a function that satis-

ﬁes above two properties and used it for generating

recommendations. We did not do much experimenta-

tion regarding different forms of decay functions.

The steps used by RECKW for expert selection

is similar to the steps used in RECK. The only dif-

ference is that each item in C = I

now con-

tributes decay(τ − t

) to v’s similarity weight, where

τ is the current time. So, items recently purchased by

v are given more importance. In the second phase,

for each item i ∈ I

, expert v contributes a score of

∗ decay(τ − t

). The scoring rule suggests that if

there are many products that an expert has purchased,

then the ones that are purchased more recently will

get higher score. The top-N items with the highest

score are recommended to the target user. The basic

steps of the algorithm are outlined below:

• For each user v ∈ U \ u, ﬁnd the co-purchased

items C = I

• Set v’s weight w

∑

|C|

j=1

decay(τ−t

vC( j)

). Select

top-K users (E) as experts.

• For each item i /∈ I

, set score s

∑

v∈E∧i∈I

∗

decay(τ−t

). Output top-N items as recommen-

dations.

4.4 Algorithm 4: Entire History with

Discounted Weight (DISCHIST)

RECK and RECKW look at k most recent purchases of

the target user u. Though the most recent purchases

KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

of a user are perhaps the most important and represen-

tative of the user’s recent interest, the past purchases

may not be totally unimportant. For users whose in-

terests have remained the same over long periods of

time, looking at some more purchases from the past

may be useful. We wanted to see if we can im-

prove the performance of recommendation by look-

ing at all past purchases of u. However, treating all

past purchases equally may decrease the performance

of the algorithm for those users whose interests have

changed over time. To avoid such a scenario, we

use the concept of importance weight, where recent

purchases are given more weight but old purchases

are given less, but non-zero weight. The importance

weight may be characterized by a decay function as

deﬁned in Equation 1. In algorithm DISCHIST, each

purchase of user u of the form (u,i,t

) is assigned an

importance weight of decay(τ − t

), where τ is the

current time. As the decay function is monotonically

decreasing in nature, users who have purchased many

of the items that u has purchased recently get higher

weight than those who have purchased many items

that u had purchased long back. The rest of the steps

are similar to that in RECKW. A brief outline of the

steps are given below.

• For each user v ∈ U \ u, ﬁnd the co-purchased

items C = I

• Set v’s weight w

∑

|C|

j=1

decay(τ−t

uC( j)

). Select

top-K users (E) as experts.

• For each i /∈ I

, set score s

∑

v∈E∧i∈I

∗

decay(τ−t

). Output top-N items as recommen-

dations.

5 EXPERIMENTAL RESULTS

5.1 Datasets Used

We used the Amazon product co-purchase metadata

and a sample of the Netﬂix data

for comparative

evaluation of the recommendation algorithms. The

Amazon dataset contains details of different products

sold on amazon. The products are of ﬁve types: Book,

Music, DVD, Video and Toy. There were not many

products for the “Toy” and “Video” categories. We

used the data for Music, DVD and Book categories

for experimentation.

There are not many publicly available datasets

for evaluating product recommendation algorithms.

http://snap.stanford.edu/data/amazon-meta.html

http://www.netﬂixprize.com/

However, several datasets are available for evaluat-

ing rating prediction algorithms. We use one such

dataset, the Netﬂix dataset, for for our experiments.

In the Netﬂix dataset, users rate different movies that

they have rented. If a user has rated a movie in this

dataset, then it can be assumed that the user was in-

terested in watching the movie. Hence if a recom-

mender system could recommend that movie just be-

fore the user decided the watch the movie, the user

could have accepted the recommendation. Based on

this intuition, we converted the Netﬂix dataset into a

purchase dataset. If a user has rated a movie, then we

assume that the user has rented/purchased the movie.

In (Kawamae et al., 2009), the authors used the Net-

ﬂix dataset for evaluating the proposed recommenda-

tion generation algorithm.

5.2 Preprocessing the Datasets

For each product, the Amazon dataset mentions its

product type, different categories that the product be-

longs to, and a list of reviewers who have reviewed

the product. In most cases, a user reviewed a product

only once. We considered these reviews as purchases.

i.e., if user u has reviewed item i, we considered that

u has purchased i. Also, for each review, the dataset

mentions the date on which the review was entered. If

user u has entered multiple reviews for product i, then

we keep the earliest review and remove the rest from

the dataset. We separated out data for each differ-

ent product type from the dataset. So, we used three

different datasets for the Amazon data, for the three

different product categories namely Book, Music and

DVD.

For the Netﬂix dataset, the sample was taken by

considering the ﬁrst 1500movies as items and the per-

sons who have rated those movies as users. If a user

had rated a movie, we consider that the user has pur-

chased the movie. In the Netﬂix dataset, each user

rates a movie at most once.

For both Amazon and Netﬂix datasets, we re-

moved from the datasets any transaction correspond-

ing to a user with fewer than m

total purchases. This

preprocessing enabled us to remove some of the non-

proliﬁc users. Also, we removed from the dataset

transactions corresponding to users who made more

than m

purchases. This was necessary so that we

could ﬁt the co-purchase network (as mentioned in

Section 5.5) in the memory. For the Amazon datasets

(Book, Music and DVD), values of m

and m

were

set to 50 and 200 respectively. For the Netﬂix dataset,

and m

were ﬁxed at 20 and 400 respectively. For

all datasets, time information was maintained in unit

of months.

UserbasedCollaborativeFilteringwithTemporalInformationforPurchaseData

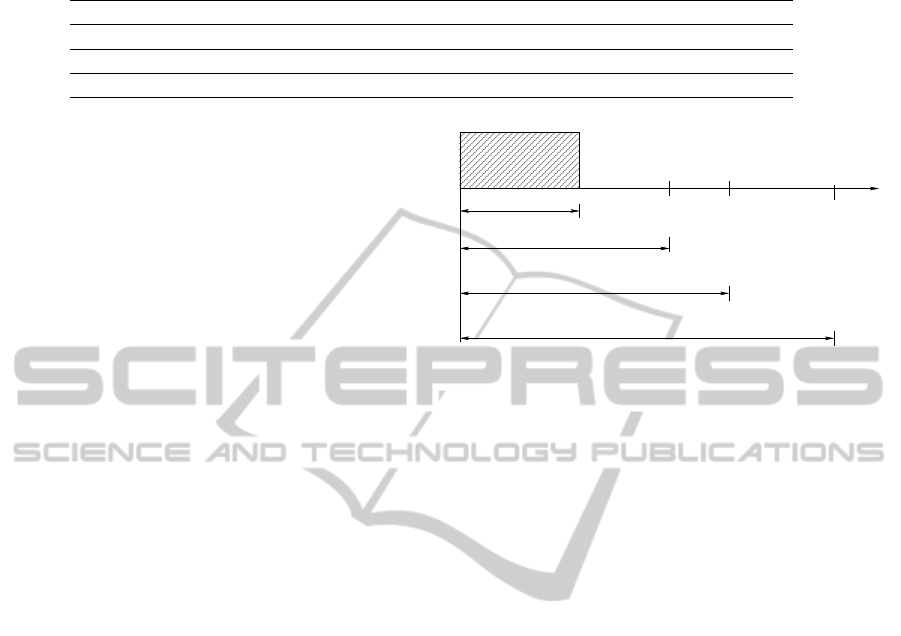
Table 1: Summary comparison of the algorithms. C is the items of importance. E is the set of experts. w

is the weight of user

v as computed during the expert selection phase. s

is the score of item i as computed in recommendation generation phase.

Algorithm CNT RECK RECKW DISCHIST

Items of interest (C) I

Contribution of i ∈ C to w

1 1 decay(τ−t

) decay(τ−t

)

Contribution of v ∈ E to s

1 w

∗ decay(τ− t

) w

∗ decay(τ− t

)

5.3 Experimental Setup

D is a dataset of product purchase transactions with

purchase timestamps. Each record in D is of the form

(u,i,t), which denotes that user u has purchased item

i at time t. We sort D in non-decreasing order of

the purchase timestamp t. The ﬁrst 20% transactions

from the dataset were kept aside initially. Let this set

be denoted by

D. Only those users who have at least

10 purchases in

D were selected as test users. The re-

maining data

D = D \

D was used for testing purpose

as follows.

For each purchase (u,i,t

) ∈

D, we wanted to

see if the algorithms were able to recommend the

item i to the user u by looking at the past purchase

records. The recommendation algorithms were al-

lowed to view purchase records from D with t < t

and were asked to come up with a list of N items as

recommendation for the test user u. We call the trans-

action (u,i,t

) as a test purchase or test transaction.

Item i is called the test item. The experimentalsetup is

shown pictorially in Figure 2. We experimented with

four different values of N: 20,50,80 and 100. We

ran the above prediction task for the ﬁrst 40 test pur-

chases of each test user. Relative performances of the

algorithms were found to be similar for the different

values of N. We report results for N = 50.

5.4 Algorithms Compared

We compared the performance of the four algorithms

described in the paper with two other algorithms from

recent literature. The algorithms suggested in (Lee

et al., 2008), (Kawamae et al., 2009) and (Zheng

and Li, 2011) use time aware collaborative ﬁltering

for recommendation. (Lee et al., 2008) divides the

items into several groups based on their launch time.

The users also were grouped according to their in-

terests in purchasing items from these different item

groups. However, the grouping and parameters as-

sociated with the groups were set in ad hoc manner.

It was not clear whether the same can be useful for

generating recommendations for other datasets. We

compare our algorithms with the algorithms proposed

in the remaining two papers, viz. the algorithm based

on Personal Innovator degree (PID) from (Kawamae

Initial training data

time

a,1

a,2

b,1

Training data to predict the purchase (a,?,t

a,1

)

Training data to predict the purchase (a,?,t

a,2

)

Training data to predict the purchase (b,?,t

b,1

)

Figure 2: The experimental setup is shown graphically. The

ﬁrst 20% of the data is used only for training. Suppose there

are only two test users a and b. a has purchased two items,

at time t

a,1

and t

a,2

. b has purchased one item at time t

b,1

We invoke the recommendation algorithm three times, at

time steps t

a,1

a,2

and t

b,1

. At time t

a,1

, the algorithms use

the entire data from the beginning to time step (t

a,1

− 1) as

observed data or training data and produce recommenda-

tions for a. We then see whether the item that a purchased

at t

a,1

is in the recommendation lists for a produced by the

algorithms. Similarly, recommendations are generated for

b (or a) at t

b,1

(or at t

a,2

) by using the data from beginning

to time step t

b,1

− 1 (or time step t

a,2

− 1) as training data.

et al., 2009) and the one based on Weighted Combina-

tion Model (WCM) from (Zheng and Li, 2011). Rec-

ommendation lists are generated by sorting the items

based on the recommendation scores assigned to them

by the algorithms.

We also considered the time-aware algorithm pro-

posed in (Ding et al., 2006). Although it is a rat-

ing prediction algorithm, we considered using it as a

baseline as it is also based on the collaborative ﬁlter-

ing framework and gives more importance to the most

recent ratings given by the users. We used it to pre-

dict the unknown ratings as the datsaets we have used

for evaluation have rating information. Top-K items

based on the predicted ratings were output as recom-

mendation. However, after some preliminary exper-

iments, we found that performance of this algorithm

was poorer than PID and WCM. So we did not use

this algorithm for detailed comparison.

5.5 Parameters and Optimizations

Algorithms RECK, RECKW and DISCHIST require

two parameters λ and γ for specifying the decay func-

tion given in Equation 1. For all the experiments, the

KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

values of λ and γ were ﬁxed at 0.1 and 0.6 respec-

tively. The length of the most recent purchase window

was set to 5. These values were selected after running

experiments on small validation sets. 40 most similar

users were selected as experts.

Early studies in user based collaborative recom-

mender systems revealed that it is common for the

target user to have highly correlated neighbors (with

high user similarity scores) that are based on a very

small number of co-purchased items. To address

this issue, it was suggested to give more signiﬁcance

weight to users who have many co-purchased items

with the target user (Herlocker et al., 2002). Follow-

ing this observation, for each test transaction, we ﬁrst

selected the top-100 users with the maximum number

of co-purchased items with the test user. We assigned

similarity weights to these 100 users. Top-40 among

these users were selected as experts. This made the

implementations faster as it was not necessary to com-

pute the similarity values for each user pair for each

test transaction. This scheme was used for all the al-

gorithms that we compared in the experimental sec-

tion. A co-purchase network of users was kept for

determining the number of co-purchased items. The

network contained an edge between two users if they

purchased at least one common item. The weight of

the edge was set to the number of items co-purchased

by them. This structure was updated in runtime after

observing each new transaction from the test set.

5.6 Evaluation Metrics

We use Hit Rate and Mean Reciprocal Rank (MRR)

metrics for comparing the performance of the algo-

rithms. Deﬁnitions of the metrics are given below.

• Hit Rate. Hit Rate of an algorithm is deﬁned as

the fraction of test transactions (

D) for which the

test item is present in the algorithm’s recommen-

dation list. Mathematically,

Hit Rate =

∑

i∈

I(i ∈ R

where R

is the recommendation list for the test

transaction i. I(p) is a boolean indicator function

that evaluates to 1 if and only if the predicate p

is true. Higher value of Hit Rate indicates better

performance.

• Mean Reciprocal Rank. We use Mean Recipro-

cal Rank (MRR) to evaluate the ability of a rec-

ommendation algorithm to place a test item near

the top of the recommendation list.

If the test item i is at rank r(i) of the recommen-

dation list, then the Reciprocal Rank (RR) of the

algorithm for i is

r(i)

. If i is not in the recommen-

dation list, then r(i) is considered as ∞. Hence the

Reciprocal Rank is 0 in that case. MRR is deﬁned

as the mean of the reciprocal ranks over all test

transactions (

D). Mathematically,

MRR =

∑

i∈

r(i)

For both Hit Rate and MRR, higher values indicate

better performance.

5.7 Comparison

For all the algorithms used for comparison, four dif-

ferent sizes (20, 50, 80, 100) of the recommenda-

tion list were considered. The ordering of the algo-

rithms according to their performances are similar for

all these list sizes. We report the results for the top-50

recommendations.

5.7.1 Amazon Music Dataset

Figure 3(a) and Figure 4(a) compare the Hit Rate

and MRR for Amazon Music dataset. According to

the results, the four algorithms deﬁned in this pa-

per perform better than the algorithms mentioned in

Section 5.4 according to both the evaluation metrics.

Among the algorithms deﬁned in this paper, the sim-

ple baseline method CNT that does not look at the

time information performs the worst. The RECK al-

gorithm that considers the last few purchases of the

target user for expert selection does better than CNT.

Algorithm RECKW that builds upon RECK by us-

ing time weighting on the experts’ purchases achieves

even better Hit Rate for this dataset. The DISCHIST

algorithm that looks at all purchases of all the users

but with discounted importance on the old purchases

achieves the highest Hit Rate.

It can be seen from ﬁgure 4(a) that RECKW has

maximum MRR, i.e. it is able to put maximum num-

ber of test items at the best (minimum) rank position

among the competitor algorithms. DISCHIST comes

next in terms of MRR. Ordering of the remaining al-

gorithms for this measure is similar to the ordering

obtained for the Hit Rate measure.

5.7.2 Amazon DVD Dataset

The results for this dataset are similar to the results

obtained for the Amazon Music dataset. Hit Rates of

the algorithms are shown in Figure 3(b). DISCHIST

gives the best performance according to this measure

and is closely followed by RECKW.

UserbasedCollaborativeFilteringwithTemporalInformationforPurchaseData

0.05

0.1

0.15

0.2

0.25

PID WCM CNT RECK RECKW DISCHIST

(a) Hit Rate for Amazon Music dataset

0.05

0.1

0.15

0.2

0.25

0.3

PID WCM CNT RECK RECKW DISCHIST

(b) Hit Rate for Amazon DVD dataset

0.05

0.1

0.15

0.2

0.25

0.3

0.35

PID WCM CNT RECK RECKW DISCHIST

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

PID WCM CNT RECK RECKW DISCHIST

(d) Hit Rate for Netﬂix dataset

Figure 3: Comparison of Hit Rate for different datasets.

Figure 4(b) compares the MRR for all the algo-

rithms. It can be seen from the ﬁgure that RECKW

achieves highest MRR. DISCHIST comes second ac-

cording to this metric. It means that ReckW and Dis-

cHist are able to put the test item near the top of the

recommended list for most of the test transactions.

5.7.3 Amazon Book Dataset

Hit Rate and MRR for the Amazon Book dataset are

shown in Figure 3(c) and Figure 4(c) respectively.

These results are somewhat different from the results

obtained for the Amazon Music dataset and Amazon

DVD dataset. Here we see that both RECKW and

RECK perform best according to Hit Rate. For MRR,

RECKW is the best algorithm and is closely followed

by RECK. DISCHIST appears at the third position for

this dataset, for both the metrics.

The results seem to indicate that for Amazon Book

dataset, it might be wise to look at only the recent

purchases of the target user. Looking at the entire

purchase history of the user, even with time weighted

discounted model as suggested in DISCHIST, might

reduce the performance of the recommendation. A

reason behind this might be that users have very fo-

cused interest for book items and this interest shifts

over time. Users purchase books belonging to only

the type(s) that they are currently interested in. As

for music and DVDs, they might have interest in sev-

eral types simultaneously and their recent purchases

are mix of items belonging to all those types.

5.7.4 Netﬂix Dataset

Experiments on the Amazon datasets showed that

the algorithms that give importance to the time-of-

purchase information achieve better performances.

This observation was corroborated by the results ob-

tained on the Netﬂix dataset.

Hit Rate comparison for the Netﬂix dataset is

shown in Figure 3(d). These results are similar to the

results observed for the Amazon Music dataset and

Amazon DVD dataset. DISCHIST performs best ac-

cording to this metric. Comparison of MRR values

KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

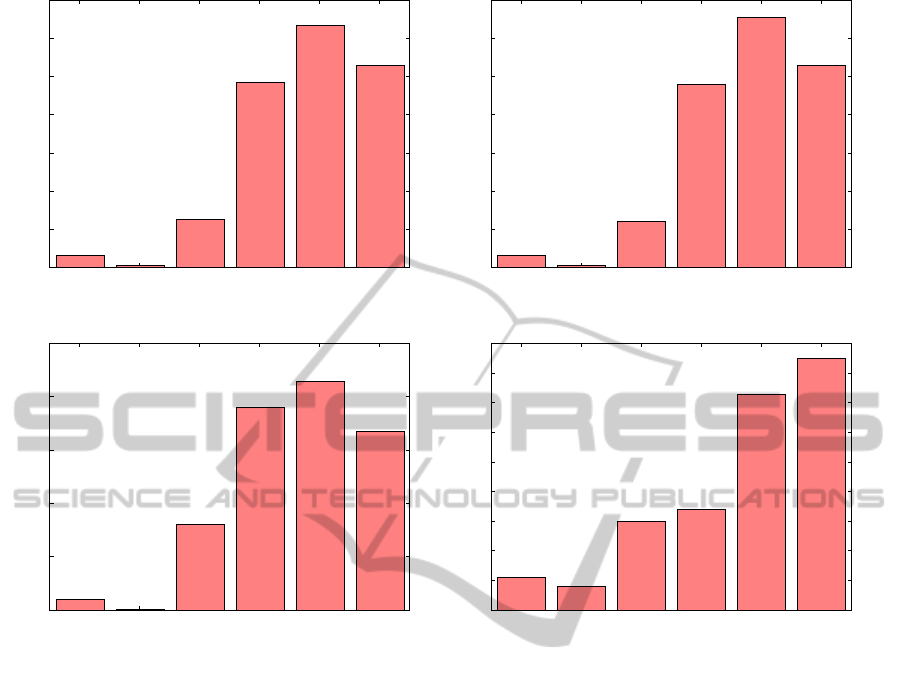
0.02

0.04

0.06

0.08

0.1

0.12

0.14

PID WCM CNT RECK RECKW DISCHIST

(a) Mean Reciprocal Rank for Amazon Music dataset

0.02

0.04

0.06

0.08

0.1

0.12

0.14

PID WCM CNT RECK RECKW DISCHIST

(b) Mean Reciprocal Rank for Amazon DVD dataset

0.05

0.1

0.15

0.2

0.25

PID WCM CNT RECK RECKW DISCHIST

0.01

0.02

0.03

0.04

0.05

0.06

0.07

0.08

0.09

PID WCM CNT RECK RECKW DISCHIST

(d) Mean Reciprocal Rank for Netﬂix dataset

Figure 4: Comparison of Mean Reciprocal Rank for different datasets.

is shown in Figure 4(d). For this dataset, DISCHIST

is the best algorithm according to MRR. Performance

of RECKW is also quite good as indicated by the ﬁg-

ure. Performances of PID and WCM algorithms are

much better for this datsaet when compared to their

performances on the other datasets mentioned above.

5.8 Discussions

Overall, DISCHIST and RECW perform the best ac-

cording to the experimental results. We consider

CNT as the baseline for our experiments. Aver-

age Hit Rates of CNT, DISCHIST and RECKW for

the test transactions over all the four datasets are

.148, .288 and .287 respectively. Hence, DISCHIST

and RECKW achieve close to 100% improvement in

Hit Rate over the baseline. Similarly, average MRR

for the three algorithms are .044,.121 and .142 re-

spectively. So, for MRR, RECW and DISCHIST

achieve close to 230% and 175% improvements re-

spectively over the baseline. Both DISCHIST and

RECKW give importance to the recent purchases of

the target user as well as the experts, and hence at-

tempt to address the issues of both user dynamics and

the item dynamics.

Looking at the individual datasets, we see that

for the Amazon Music and DVD datasets and the

Netﬂix dataset, DISCHIST performs the best accord-

ing to Hit Rate. RECKW and RECK come next in

terms of performance. According to MRR, algo-

rithms RECKW and DISCHIST perform the best. The

trend is little different for the Amazon Book dataset

where RECKW and RECK are better than DISCHIST.

It means that for this dataset, the algorithms should

only consider the most recent purchases of the test

user and use that for expert selection. This may be

due to the fact that users have very focused interest in

a very limited set of categories or sub-categories for

book items. It appears that the size of that interest set

is much smaller for book data, when compared with

the same for Music, DVD or Movie data. Hence giv-

ing importance to purchases made long back, even if

the importance weights for those items are low, act

as distraction for the recommendation algorithms. In

this work, we have used the same parameters to spec-

ify the decay function for all the datasets. However,

UserbasedCollaborativeFilteringwithTemporalInformationforPurchaseData

depending on the domain of the items or the selling

trend of the individual items, different parameters can

be used for the decay function for different datasets or

even for individual items.

6 CONCLUSIONS

In this work, we have explored a few time-aware user

based collaborativeﬁltering algorithms for the recom-

mendation problem. We have analyzed the beneﬁts

of using the time-of-purchase information in both the

phases of expert selection and recommendation gen-

eration. Giving importance to time factor in the ex-

pert selection phase tries to address the problem of the

target user’s interest shift. Giving importance to the

most recent items purchased by the experts attempts

to capture the item dynamics. Experimental results

indicate that recommendationperformancecan be im-

proved by giving more importance to the recent pur-

chases of both the user and the experts.

ACKNOWLEDGEMENTS

The ﬁrst author is supported by a PhD Fellowship

from Microsoft Research India.

REFERENCES

Campos, P. G., Bellog´ın, A., D´ıez, F., and Chavarriaga, J. E.

(2010). Simple time-biased knn-based recommenda-

tions. In Proceedings of the Workshop on Context-

Aware Movie Recommendation, CAMRa ’10, pages

20–23.

Deshpande, M. and Karypis, G. (2004). Selective markov

models for predicting web page accesses. ACM Trans.

Internet Technol., 4:163–184.

Ding, Y. and Li, X. (2005). Time weight collaborative ﬁl-

tering. In Proceedings of the 14th ACM international

conference on Information and knowledge manage-

ment, CIKM ’05, pages 485–492.

Ding, Y., Li, X., and Orlowska, M. E. (2006). Recency-

based collaborative ﬁltering. In Proceedings of the

17th Australasian Database Conference - Volume 49,

ADC ’06, pages 99–107.

Herlocker, J., Konstan, J. A., and Riedl, J. (2002). An em-

pirical analysis of design choices in neighborhood-

based collaborative ﬁltering algorithms. Inf. Retr.,

5:287–310.

Kawamae, N., Sakano, H., and Yamada, T. (2009). Per-

sonalized recommendation based on the personal in-

novator degree. In Proceedings of the third ACM con-

ference on Recommender systems, RecSys ’09, pages

329–332.

Koren, Y. (2008). Factorization meets the neighborhood:

a multifaceted collaborative ﬁltering model. In Pro-

ceeding of the 14th ACM SIGKDD international con-

ference on Knowledge discovery and data mining,

KDD ’08, pages 426–434.

Koren, Y. (2009). Collaborative ﬁltering with temporal dy-

namics. In Proceedings of the 15th ACM SIGKDD

international conference on Knowledge discovery and

data mining, KDD ’09, pages 447–456.

Lee, T. Q., Park, Y., and Park, Y.-T. (2008). A time-based

approach to effective recommender systems using im-

plicit feedback. Expert Syst. Appl., 34:3055–3062.

Parameswaran, A. G., Koutrika, G., Bercovitz, B., and

Garcia-Molina, H. (2010). Recsplorer: recommen-

dation algorithms based on precedence mining. In

Proceedings of the 2010 international conference on

Management of data, SIGMOD ’10, pages 87–98.

Rendle, S., Freudenthaler, C., and Lars, S.-T. (2010). Fac-

torizing personalized markov chains for next-basket

recommendation. In Proceedings of the 19th inter-

national conference on World wide web, WWW ’10,

pages 811–820.

Rongfei, J., Maozhong, J., and Chao, L. (2010). Using tem-

poral information to improve predictive accuracy of

collaborative ﬁltering algorithms. In Proceedings of

the 2010 12th International Asia-Paciﬁc Web Confer-

ence, APWEB ’10, pages 301–306.

Shani, G., Heckerman, D., and Brafman, R. I. (2005). An

mdp-based recommender system. J. Mach. Learn.

Res., 6:1265–1295.

Zheng, N. and Li, Q. (2011). A recommender system based

on tag and time information for social tagging sys-

tems. Expert Syst. Appl., 38:4575–4587.

KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval