
Generation of Non-redundant Summary based on Sentence
Clustering Algorithms of NSGA-II and SPEA2
Jung Song Lee
1
, Han Heeh Ham
2
, Seong Soo Chang
3
and Soon Cheol Park
1
1
Division of Electronics and Information Engineering, Chonbuk National University, Jeonju, Korea
2
Department of Archeology and Cultural Anthropology, Chonbuk National University, Jeonju, Korea
3
Department of Korean Language and Literature, Chonbuk National University, Jeonju, Korea
Keywords: Automatic Document Summarization, Sentence Clustering, Extractive Summarization, Multi-objective
Genetic Algorithm, NSGA-II, SPEA2, Normalized Google Distance.
Abstract: In this paper, automatic document summarization using the sentence clustering algorithms, NSGA-II and
SPEA2, is proposed. These algorithms are very effective to extract the most important and non-redundant
sentences from a document. Using these, we cluster similar sentences as many groups as we need and
extract the most important sentence in each group. After clustering, we rearrange the extracted sentences in
the same order as in the document to generate readable summary. We tested this technique with two of the
open benchmark datasets, DUC01 and DUC02. To evaluate the performances, we used F-measure and
ROUGE. The experimental results show the performances of these MOGAs, NSGA-II and SPEA2, are
better than those of the existing algorithms.
1 INTRODUCTION
Document summarization has become an important
technique in information retrieval system. This
technique that can assist and interpret text
information has developed with two different
techniques: extractive and abstractive ways of
summarization (Shen et al., 2007). The extractive
summarization techniques are commonly used in the
document summarization.
The extractive summarization techniques can be
classified into two groups: supervised extractive
summarization techniques regarded as two class
classification problems (positive sample and
negative sample) in the sentence level. Unsupervised
extractive summarization techniques use the
heuristic rule in order to select the sentence
providing this most important information in the
summary directly.
We applied the clustering technique which is the
unsupervised categorization techniques to reduce
redundancy on summarizing results. Redundancy
means that the selected sentences have same terms
due to the high occurrences of those terms.
Using clustering technique, the sentences in a
document are clustered into several groups. The
main sentence of each group will be a candidate of
the summarized sentences. This technique is very
effective to reduce redundancy in the summary.
Because, extracted sentences include the important
content of a document very much and the selected
the sentences without the similarity with the other
sentences in sentence cluster. Moreover, each cluster
can concern to include the main topic of the
document. Therefore, the application of clustering
can be considered as one method for solving
redundancy in the summary of the extractive
summarization. For sentence clustering, we
introduce the recently proposed Multi-Objective
Genetic Algorithms (MOGA) which is based on the
optimization problem (Lee et al., 2011).
The MOGAs was applied in document clustering
to solve the premature convergence problem of
Genetic Algorithm (GA) (Song and Park, 2009) and
the parameter dependence of Fuzzy Logic based GA
(FLGA) (Song and Park, 2010). The document
clustering using MOGAs shows the higher
performance than the other clustering algorithms.
Since, MOGAs is further applied to sentence
clustering.
This paper is organized as follows: Details of
automatic document summarization using sentence
clustering based on MOGAs are described in Section
176
Lee J., Hahm H., Chang S. and Park S..
Generation of Non-redundant Summary based on Sentence Clustering Algorithms of NSGA-II and SPEA2.
DOI: 10.5220/0004134501760182
In Proceedings of the 4th International Joint Conference on Computational Intelligence (ECTA-2012), pages 176-182
ISBN: 978-989-8565-33-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
2. Experiment results are given in Section 3.
Conclusions and future work are given in Section 4.
2 AUTOMATIC DOCUMENT
SUMMARIZATION USING
SENTENCE CLUSTERING
BASED ON MOGA
First of all, we defined sentence clustering problem
as the Multi-Objective Optimization Problem
(MOOP) (Censor, 1977) with two cluster validity
indices. MOOP is to find the optimal solutions using
several objective functions. This offers us a chance
to solve the premature convergence of GA because
when one objective function traps into the local
optimal solution, the other objective function can
interrupt it. To solve MOOP, various algorithms
were suggested. However, there are certain
limitations (Konak et al., 2006). In this paper,
NSGA-II (Deb et al., 2002) and SPEA2 (Zitzler et
al., 2002) are adopted among the MOGAs to solve
this problem of MOOP.
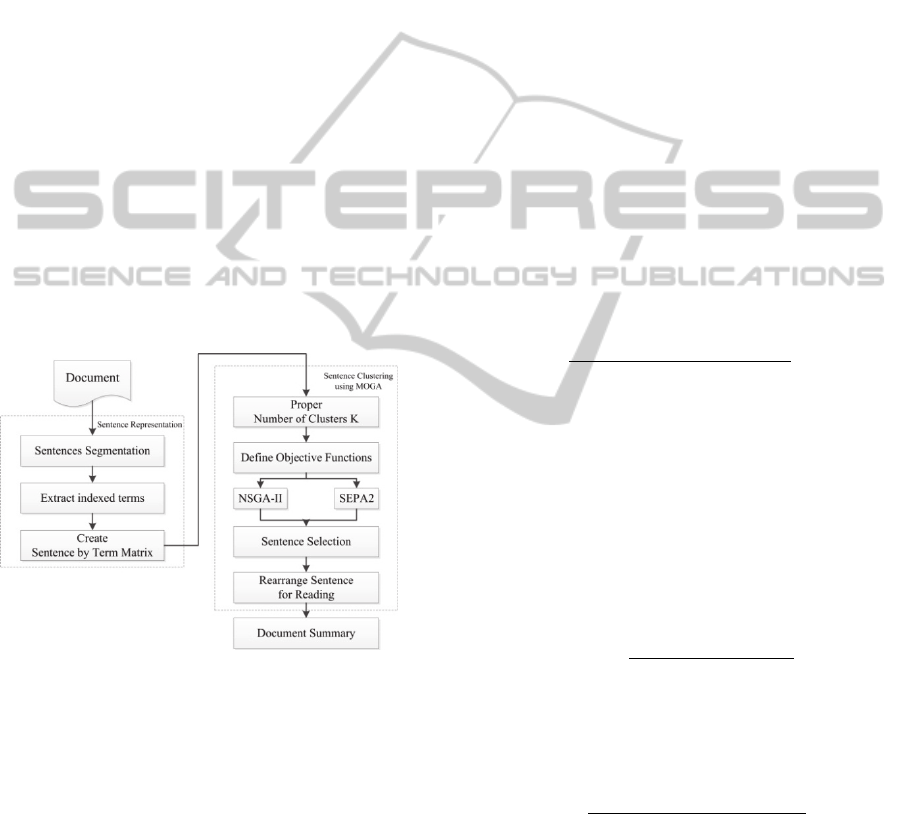
Figure 1: Procedure of automatic document summarization
using sentence clustering based on MOGAs.
The procedure of our summarization system
based on MOGAs is shown in Figure 1. First,
sentences are represented by using IR techniques
(Sentence Segmentation, Stop Word Remove,
Porter’s Stemming). Second, the sentences are
clustered by using MOGAs, NSGA-II and SPEA2,
to reduce the redundancy. Then, the sentences which
are the weightiest terms in clusters are selected.
Finally, the selected sentences are rearranged as in
the document for reading.
2.1 Sentence Representation and
Similarity Measure between
Sentences
In most existing document clustering algorithms,
documents are represented using the Vector Space
Model (VSM). The representation and similarly
using VSM is not very efficient for sentence. So, we
have applied another sentence representation and
similarly techniques. Each sentence S
n
is defined by:
S
n
= <T
n
,
1
, T
n
,
2
, …, T
n
,
m
>, where m is the number of
indexed terms in a sentence S
n
. That is, a sentence S
n
is represented as sequence of terms existing in the
document.
Next, we present a method to measure similarity
between sentences using the Normalized Google
Distance (NGD) (Cilibrasi and Vitányi, 2007). NGD
takes advantage of the number of hits returned by
Google search engine to compute the semantic
distance between two sentences.
NGD is defined the global and local similarity
measure between terms in sentences. First, the
global similarity measure between terms t
i
and t
j
is
defined by the formula:
NGD
,
max
log
,log
log
,
log
min
log
,log
,
(1)
where f
g
(t
i
) and f
g
(t
j
) denote for the numbers of web
pages containing the search terms t
i
and t
j
respectively. f
g
(t
i
, t
j
) is the number of web pages
containing both terms t
i
and t
j
. N
google
is the total
number of web pages indexed by Google search
engine.
Using the definition of global similarity measure
between terms as Equation (1), the global sentence
similarity measure between sentences S
k
and S
l
is
given by:
,
∑∑
NGD
,
∈
∈
,
(2)
where m
i
and m
j
represent the numbers of terms in
sentences S
k
and S
l
respectively.
Similarly, the local similarity measure between
terms t
i
and t
j
is defined by:
NGD
,
max
log
,log
log
,
log
min
log
,log
,
(3)
where f
l
(t
i
) and f
l
(t
j
) denote the numbers of sentences
containing terms t
i
and t
j
, respectively, in document
D. f
l
(t
i
, t
j
) is the number of sentences containing both
t
i
and t
j
, and n is the total number of sentences in
document D. Also, using Equation (3), the local
sentence similarity measure is given by:
GenerationofNon-redundantSummarybasedonSentenceClusteringAlgorithmsofNSGA-IIandSPEA2
177

,
∑∑
NGD
,
∈
∈
,
(4)
Finally, the overall sentence similarity measure
between sentences S
k
and S
l
is defined as a product
of global and local similarity measures:
NGD
,
,
,
,
(5)
2.2 Generating the Proper Number of
Clusters
The number of clusters (topics) in each document is
not given before summarization. Thus, we need to
determine the proper number of cluster a prior. For
this, we used the approach based on the distribution
of terms in the sentences which are defined as:
|
|
∑|
|
⋃
∑|
|
,
(6)
where |d| is the number of terms in document d and
n is number of sentences in d. Authors of the paper
(Aliguliyev, 2009) provide two cases in which the
numbers of clusters are bounded to the k, for
clustering n sentences. That is, we always have 1 k
n. The definition of (6) gives the interpretation of k
as the proper number of clusters in terms of average
number of terms. Once cluster number is determined
by this way, MOGAs is implemented in our study
for sentence clustering.
2.3 Define MOOP for Sentence
Clustering
MOOP for the sentence clustering is defined
as:argmax
∈
F
CH
∧F
DB
, where CH and
DB are represented as CH index (Calinski and
Harabasz, 1974) and DB index (Davies and Bouldin,
1979) for the objective functions of MOGAs. P is
the population and P = {C
1
, C
2
,…, C
i
,…, C
n
}. C
i
is a
chromosome and C
i
= {CN
1
, CN
2
,…, CN
j
,…, CN
m
}.
CN
j
is the cluster number assigned to a sentence and
1 CN
j
K, n is the number of chromosomes in a
population, m is the number of sentences and K is
the number of clusters.
2.4 Chromosome Encoding and
Evolution Principles
Each chromosome in the population is initially
encoded by a number of m genes with an integer
value in the range 1 ~ K. m is the number of
sentences in a document and K is the number of
clusters. For example, assuming that m = 9, K = 3
and C
i
= {2, 3, 1, 1, 1, 2, 3, 3, 1}, the first sentence is
allocated to the second cluster, the second sentence
to the third cluster and so on.
The time complexities of NSGA-II and SPEA2
are O(MN
2
) and O(MN
2
logN) respectively. Where,
M is the number of objective functions and N is the
population size. MOGAs using the cluster valid
indices as the objective functions require the higher
computational complexity. So, we have applied the
simple cluster validity indices CH index and DB
index for the sentence clustering using MOGAs.
And multi-point crossover and uniform mutation are
adopted in the evolution operators.
2.5 Objective Functions
When CH index is the maximum value by using
inter-group variance and between-group variance,
clustering result is good cluster. CH index is given
by:
CH
/
/
,
(7)
where B stands for Between Group Sum of Squares
and W stands for Within Group Sum of Squares. n is
the number of sentences, k is the number of clusters.
DB index is based on similarity measure of
clusters (R
ij
) whose bases are the dispersion measure
of a cluster (s
i
, s
j
) and the cluster dissimilarity
measure (d
ij
). In similarity, maximum value is
considered as the good cluster when the cluster is
evaluating with the cosine similarity. DB index
given by:
DB
∑
,
(8)
Subsequently, R
i
is:
max
,and
1⋯
. (9)
R
ij
defined as:
,
(10)
where n
c
is number of clusters. s
i
and s
j
are the
average similarities of sentences in cluster centroids,
i and j respectively. d
ij
is the dissimilarity between
the cluster centroids, i and j.
2.6 Sentence Clustering using
NSGA- II and SPEA2
Various MOGAs have been used in many
applications and their performances are tested in
several studies, i.e., PESA, NSGA-II, SPEA2 and
etc. NSGA-II and SPEA2 are easy to implement and
don’t have parameter for diversity in a population
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
178
(Konak et al., 2006). So, we applied these
algorithms to sentence clustering. In MOGAs, the
solution set contain a large number of solutions.
That is, sentence clustering using the MOGAs does
not return a single cluster solution. The
identification of promising solutions from the
solution set has been investigated in several papers
called Decision Maker (DM). But, these techniques
are very difficult. So, we manually select one of the
best cluster solutions in the Pareto optimal solution
set (Censor, 1977).
The procedure of sentence clustering using
NSGA-II and SPEA2 are given as follows.
Sentence Clustering Procedure using NSGA-II
Step
1:
Create initially a population P
0
, Set population size
N and Set generation t=0
Step
2:
Calculate the objective functions (CH and DB
index) of each solutions in P
t
Step
3:
Create offspring population Q
t
Step
4:
Set R
t
=P
t
+Q
t
Step
5:
Calculate the objective functions (CH and DB
index) of each solutions in R
t
Step
6:
Identify the non-dominated fronts F
1
,F
2
,...,F
k
in R
t
Step
7:
Calculate Crowding distance of the solutions in
each F
k
Step
8:
Apply evolution operators to P
t+1
to create
offspring population Q
t+1
Step
9:
If the stopping criterion is satisfied, stop and return
P
t
, else Set t=t+1, and go
Step
4
Sentence Clustering Procedure using SPEA2
Step
1:
Create initially a population P
0
, Set archive E
0
, Set
population size N, Set archive size N
E
and Set
generation t=0
Step
2:
Calculate the objective functions (CH and DB
index) of each solutions in P
t
+E
t
Step
3:
Calculate the fitness of each solutions in P
t
+E
t
Step
5:
Copy all non-dominated solutions in P
t
+E
t
to E
t+1
using the truncation operator
Step
6:
If the stopping criterion is satisfied, stop and return
E
t+1
, else go on
Step
7:
Select parents from E
t+1
and Apply evolution
operators to the parents to create offspring N
P
population
Step
8:
Copy offspring to P
t+1
, Set t=t+1, go
Step
2
2.7 Sentence Selection and
Rearrangement of Sentences for
Reading
To select the important sentence in a sentence
cluster, we use the weights of sentences in each
cluster proposed in the paper of Pavan and Pelillo
(2007). The Weight of Sentence S
i
in sentence
cluster C
p
will be defined by the following recursive
formula as:
1, i
f
1
∑
Φ
,
∈
,otherwise
.
(11)
Where, C
p
is nonempty sentence cluster and S
i
, S
j
are sentences in C
p
.
Subsequently,
C
p
(S
j
, S
i
) is:
Φ
,
NGD
,
.
(12)
And awdeg
C
p
(S
j
) is:
∑
NGD
,
∈
.
(13)
Consequently, top ranked sentences are selected in
sentence cluster with reversed order of WOS
C
p
value.
The summary is provided by compounding the
important sentences extracted from each sentence
cluster. But, it is needed to rearrange the sentences
for reading. Each sentence cluster has the
information of the indices of the sentences which are
the same as the sequence order as in a document.
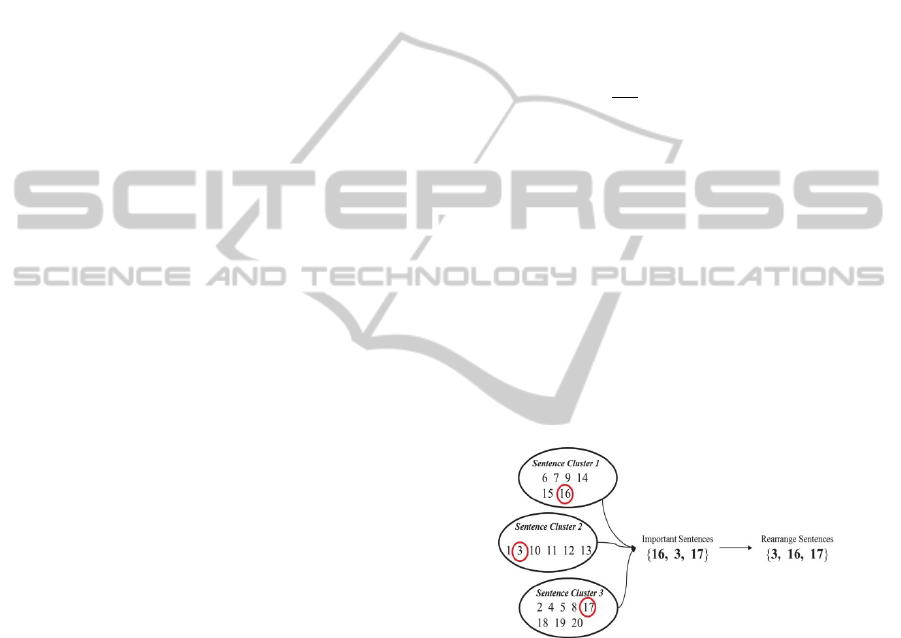
After selecting the utmost weighted sentences in
the clusters, we sort the sentences with their indices
and then return the sentences in the sorted order.
Figure 2 shows the procedure or the sentence
rearrangement.
Figure 2: Rearrangement of the sentences selected from
each cluster.
3 EXPERIMENT RESULTS
3.1 Datasets and Evaluation Metrics
We conduct our method of MOGAs for extractive
summarization on two document datasets DUC01
and DUC02 and the corresponding 100-word
summaries generated for each document. The
DUC01 and DUC02 as the most-widely adopted
benchmark datasets in the document summarization
are the open source datasets published by Document
Understanding Conference (http://duc.nist.gov). The
GenerationofNon-redundantSummarybasedonSentenceClusteringAlgorithmsofNSGA-IIandSPEA2
179

DUC01 and DUC02 contain 147 and 567
documents-summary pairs respectively. These
datasets are clustered into 30 and 59 topics,
respectively. In those document datasets, stop word
removal and the terms were stemmed using Porter’s
stemming.
To evaluate the performances of the algorithms,
we use two measurements. The first measurement is
F-measure (Fragoudis, 2005) which uses a generic
metric to evaluate the performance of IR. The
second measurement is the ROUGE toolkit (Lin et
al., 2003). It has been shown that ROUGE is very
effective for measuring document summarization
and it measures the summary quality too by counting
the overlapping units between reference summary
and candidate summary. And the number of
population in MOGAs is 300. These algorithms are
terminated when the number of generations reaches
1000 or when the iterations without improvement
consecutively reach 20.
3.2 Performance and Discussion
In this section, we compare the summary
performances of MOGAs with those of other five
methods, such as CRF (Shen et al., 2007),
Manifold–Ranking (Wan et al., 2007), NetSum
(Svore et al., 2007), QCS (Dunlavy et al., 2007), and
SVM (Yeh et al., 2004) which are widely used in the
automatic document summarization. Table 1 and
Table 2 show the results of all the methods in terms
F-measure, ROUGE-1 and ROUGE-2 metrics on
DUC01 and DUC02 datasets, respectively.
From Table 1 and Table 2, we can see that the
performances of MOGAs (NSGA-II and SPEA2) are
better than those of other five methods in terms of
F-measure, ROUGE-1 and ROUGE-2.
Table 1: Summarization performance on DUC01 dataset.
Methods F-measure ROUGE-1 ROUGE-2
NSGA-II
0.49821 0.49620 0.19878
SPEA2
0.49125 0.48072 0.19247
CRF 0.46405 0.45525 0.17665
Manifold
Ranking
0.43365 0.42865 0.16354
NetSum 0.47014 0.46231 0.16698
QCS 0.44192 0.43852 0.18457
SVM 0.44628 0.43254 0.17002
Table 2: Summarization performance on DUC02 dataset.
Methods F-measure ROUGE-1 ROUGE-2
NSGA-II
0.48312 0.47568 0.13456
SPEA2
0.47528 0.47001 0.13012
CRF 0.46003 0.44401 0.10873
Manifold
Ranking
0.41926 0.42536 0.10528
NetSum 0.46158 0.45562 0.11254
QCS 0.42116 0.45002 0.10547
SVM 0.43152 0.43785 0.10745
We also compare MOGAs with other five
methods in Table 3. In order to show the
improvements of MOGAs with other five methods,
we use relative improvement as:
othermethods
100.
Table 3: Comparison of Summarization performance.
Datasets Metrics
CRF Manifold Ranking NetSum QCS SVM
NSGA-II SPEA2 NSGA-II SPEA2 NSGA-II SPEA2 NSGA-II SPEA2 NSGA-II SPEA2
DUC01
F-measure (+)7.36% (+)5.86% (+)14.88% (+)13.28% (+)5.97% (+)4.49% (+)12.74% (+)11.16% (+)11.64% (+)10.08%
ROUGE-1 (+)9.00% (+)5.59% (+)15.76% (+)12.15% (+)7.33% (+)3.98% (+)13.15% (+)9.62% (+)14.72% (+)11.14%
ROUGE-2 (+)12.53% (+)8.96% (+)21.55% (+)17.69% (+)19.04% (+)15.27% (+)7.70% (+)4.28% (+)16.92% (+)13.20%
DUC02
F-measure (+)5.02% (+)3.32% (+)15.23% (+)13.36% (+)4.67% (+)2.97% (+)14.71% (+)12.85% (+)11.96% (+)10.14%
ROUGE-1 (+)7.13% (+)5.86% (+)11.83% (+)10.50% (+)4.40% (+)3.16% (+)5.70% (+)4.44% (+)8.64% (+)7.34%
ROUGE-2 (+)23.76% (+)19.67% (+)27.81% (+)23.59% (+)19.57% (+)15.62% (+)27.58% (+)23.37% (+)25.23% (+)21.1%
Table 4: Summarization Result of MOGAs using NGD, Cosine and Euclidean measures.
Datasets Measures
F-measure ROUGE-1 ROUGE-2
NSGA-II SPEA2 NSGA-II SPEA2 NSGA-II SPEA2
DUC01
NGD 0.49821 0.49125 0.49620 0.48072 0.19878 0.19247
Cosine 0.48544 0.48012 0.47251 0.46758 0.18254 0.18021
Euclidean 0.46581 0.46002 0.45912 0.45012 0.17096 0.16993
Improvement (Cosine)
(+)2.64% (+)2.32% (+)5.01% (+)2.81% (+)8.90% (+)6.80%
Improvement (Euclidean)
(+)6.96% (+)6.79% (+)8.08% (+)6.80% (+)16.27% (+)13.26%
DUC02
NGD 0.48312 0.47528 0.47568 0.47001 0.13456 0.13012
Cosine 0.47692 0.46993 0.46553 0.45964 0.12001 0.11936
Euclidean 0.46238 0.45863 0.45523 0.45008 0.11997 0.10988
Improvement (Cosine)
(+)1.30% (+)1.14% (+)2.18% (+)2.26% (+)12.12% (+)9.01%
Improvement (Euclidean)
(+)4.49% (+)3.63% (+)4.49% (+)4.43% (+)12.16% (+)18.42%
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
180

The positive sign (+) stands for improvement,
and the negative sign (-) stands for the opposite. In
Table 3, the performances of MOGAs are about 9%,
16%, 8%, 12% and 13% higher than CRF, Manifold
Ranking, NetSum, QCS and SVM respectively.
In Table 4, we compare the performances of
MOGAs using different similarity measures (Cosine,
Euclidean, and NGD) to test the effectiveness of the
NGD-based dissimilarity measure. Consequently,
MOGAs with NGD performs better than Cosine and
Euclidean measures.
4 CONCLUSIONS
We have presented automatic document
summarization using sentence clustering based on
MOGAs, NSGA-II and SPEA 2, to improve the
performance of summarization. These MOGAs with
the CH and DB-indexes are compared to several
existing summarization methods on the open
DUC01 and DUC01 datasets. Since the conventional
document similarity measures are not suitable for
computing similarity between sentences, a
normalized Google distance is used.
Even though the MOGAs are no novelty in the
methodology, these algorithms have been proved for
the good clustering algorithms. Also, these are not
yet been studied for the document summarization.
We tested them with various methods (five
summarization methods) and various datasets
(DUC01 contain 147 and DUC02 contain 567) to
prove their good performances. Consequently,
NSGA-II and SPEA 2 showed the higher
summarization performances than other methods.
The performances of these MOGAs are about 9%,
16%, 8%, 12% and 13% higher than CRF, Manifold
Ranking, NetSum, QCS and SVM respectively.
In the near future, we will apply semantic
analysis to sentence similarity to reduce the
redundancy problem. And more various cluster
indices as objective functions will be tested to
improve the clustering performances.
ACKNOWLEDGEMENTS
This research was supported by Basic Science
Research Program through the National Research
Foundation of Korea (NRF) funded by the Ministry
of Education, Science and Technology (No. 2012-
0002004) and partially supported by the second
stage of Brain Korea 21 Project in 2012.
REFERENCES
Shen, D., Sun, J. T., Li, H., Yang, Q., and Chen, Z. 2007.
Document summarization using conditional random
fields. In Proceedings of IJCAI. 2862-2867.
Lee, J. S., Choi, L. C., and Park, S. C., 2011. Multi-
objective genetic algorithms, NSGA-II and SPEA2,
for document clustering. Communications in
Computer and Information Science. 257:219-227.
Song, W., and Park, S. C., 2009. Genetic algorithm for
text clustering based on latent semantic indexing.
Computers and Mathematics with Applications.
57:1901-1907
Song W., and Park, S. C., 2010. Latent semantic analysis
for vector space expansion and fuzzy logic-based
genetic clustering. Knowledge and Information
Systems. 22:347-369.
Censor, Y., 1977. Pareto optimality in multiobjective
problems. Applied Mathematics and Optimization.
4:41-59.
Knonak, A., Coit, D. W and Smith, A. E., 2006. Multi-
objective optimization using genetic algorithms : A
tutorial. Reliability Engineering and System Safety.
91:992-1007.
Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T., 2002.
A fast elitist multiobjective genetic algorithm: NSGA-
II. IEEE Transaction on Evolutionary Computation.
6(2):182-197.
Zitzler, E., Laumanns, M., and Thiele, L., 2002. SPEA2:
Improving the strength pareto evolutionary algorithm.
Proceedings of the EROGEN.
Cilibrasi, R. L., Vitányi, P. M. B., 2007. The Google
similarity measure. IEEE Transaction on Knowledge
and Data Engineering. 19:370-383.
Aliguliyev, R. M., 2009. A new sentence similarity
measure and sentence based extractive technique for
automatic summarization. Expert Systems with
Applications. 36 (4):7764-7772.
Calinski, T., Harabasz, J., 1974. A dendrite method for
cluster analysis. Communucations in Statistics.
Davies, D. L., Bouldin, D. W., 1979. A cluster separation
measure. IEEE transactions on Pattern analysis and
Machine Intelligene.
Pavan, M., Pelillo, M., 2007. Dominant sets and pairwise
clustering. IEEE Transactions on Pattern Analysis and
Machine Learning. 29:167-172.
Fragoudis, D., Meretakis, D., and Likothanassis, S., 2005.
Best terms:an efficient feature-selection algorithm for
text categorization. Knowledge and Information
Systems.
Lin, C. Y., Hovy, E. H., 2003. Automatic evaluation of
summaries using N-gram co-occurrence statistics. In
Proceedings of the NAACL on HLT 2003. 1:71-78.
Wan, X., Yang, J., and Xiao, J. 2007. Manifold-ranking
based topic-focused multi-document summarization.
In Proceedings of the 20th international joint
conference on artificial intelligence. 2903-2908.
Svore, K. M., Vanderwende, L., and Burges, C. J. C. 2007.
Enhancing single-document summarization by
GenerationofNon-redundantSummarybasedonSentenceClusteringAlgorithmsofNSGA-IIandSPEA2
181

combining RankNet and third-party sources. In
Proceedings of the EMNLP-CoNLL. 448-457.
Dunlavy, D. M., O’Leary, D. P., Conroy, J. M., and
Schlesinger, J. D., 2007. QCS: A system for querying,
clustering and summarizing documents. Information
Processing and Management. 43:1588-1605.
Yeh, J. Y., Ke, H. R., Yang, W. P., and Meng, I. H., 2005.
Text summarization using a trainable summarizer and
latent semantic analysis. Information Processing and
Management. 41:75-95.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
182
