
Towards Semantic Summaries over Ontologies
Sebastian Wandelt
1
and Ralf M
¨
oller
2
1
WBI, Humboldt Universit
¨
at zu Berlin, Berlin, Germany
2
STS, Hamburg University of Technology, Hamburg, Germany
Keywords:
Ontologies, Description Logics, Semantic Summaries.
Abstract:
Industry is increasingly dependent on the gathering and processing of data to support crucial product develop-
ment activities. However, support systems for engineers or computer scientists may need to consider terabytes
of data, making it very hard to automatically extract useful information. Querying data repositories in order to
extract just the right information for the situation at hand remains a challenging problem.
We propose a notion of semantic summaries on top of description logic knowledge bases that supports query-
ing and summarizing information in large (ontological) data repositories. The idea of a semantic summary is
to characterize the result set from a broader perspective, instead of describing each domain object. We show
that our summarization approach scales for benchmark ontologies up to several million assertional axioms.
1 INTRODUCTION
Industry is increasingly dependent on the gathering
and processing of data to support decision making
and other activities critical to their business. How-
ever, support systems for engineers, including soft-
ware engineers, need to gather information from data
stores that grow up to petabyte size, making efficiency
in information retrieval increasingly difficult. Query-
ing data repositories in order to extract just the right
information for the situation at hand is a challenging
task.
When dealing with huge data sets, it can be help-
ful to compute any kind of synopses and summaries
over the data for two purposes. First, from a query
answering system point of view, it might be more ef-
ficient to answer (transformed) queries over a summa-
rization, because of reduced complexity of the input.
Second, from a user’s point of view, it can be easier
to explain/comprehend particular relations (e.g. sub-
sumptions, individual relations, etc.) in the ontology.
The underlying idea for creating synopses and sum-
marizations is closely related to notions of similarity.
First, we discuss similarity in the case of synopses.
Technically, synopses can be created in several ways:
• Spatial synopses: Given a particular snapshot
(representation of a point of time), a similarity re-
lation/function is computed, which assigns a sim-
ilarity measure for any two entities (concepts, in-
dividuals, etc.) in an ontology. For example, in a
clinical setting, two patients can be treated simi-
lar, if they share a particular amount of symptoms.
In a synopsis, these patients might be merged to-
gether and only unmerged/unfolded on further re-
quest. The scenario is depicted in Figure 1.
Figure 1: Semantic summary.
Joe and Sarah share symptoms Fever and
Headache in our example. For some queries it
might sufficient to merge Joe and Sarah into one
individual, which then has e.g. only Fever and
Headache, or, Fever, Headache, Shoulder injury
and Dry cough. The outcome after reasoning
over summarizations clearly depends on the cho-
sen strategy. Especially in a clinical setting, for
some queries, it is important to retain soundness
and completeness in a synopsis, because we do
not want to draw wrong conclusions about any of
our patients. On the other hand, there might be
queries, which do not need to distinguish details
about Joe and Sarah, e.g. assume we want to find
out all patients with Fever only.
196
Wandelt S. and Möller R..
Towards Semantic Summaries over Ontologies.
DOI: 10.5220/0004134601960201
In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2012), pages 196-201
ISBN: 978-989-8565-30-3
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

• Temporal synopses: the idea is to use similarity of
an individual over time. For example, assume the
scenario shown in the Figure 2. There we show
one possible progress of a disease for Joe. If we
want to query for people with shoulder injuries
only, we do not need to distinguish the instances
of Joe over time. On the other hand, if we have
a query to find patients with rising symptoms for
flue, it is inevitable to consider all changes of in-
formation on Joe.
Figure 2: Semantic summary.
• Diagonal synopses: Combine Spatial and Tem-
poral Synopses. This area is widely unexplored,
but seems to have high potential to analyze large
amounts of fluctuant data.
The challenges about synopses are twofold. First,
the choice of the strategy (which entities to treat sim-
ilar) is crucial to determine its reasoning and expla-
nation capabilities. Second, it is important to iden-
tify which synopses should be kept up-to-date for an
ontology. Summaries can be seen as an extension of
synopses. The idea is to get away from told instance
information in ontologies to determine a kind of ab-
straction of the stored assertional data. Going back
to our clinical example, the idea can be visualized as
shown in Figure 3.
Figure 3: Semantic summary.
For example, in a summary, we only know that
there is a patient with Chickenpox. Furthermore, we
know that there are three people who have Headache,
and possible share Fever and Shoulder Injuries. This
summary can be used to talk about the general situa-
tion, e.g. allocation of beds, in the hospital. With ex-
isting technologies this is not yet possible. Although
one can create statistics over ontologies by predefined
aggregate queries, these queries do not adapt to new
situations (e.g. new diseases).
With summaries, these statistics are just created
automatically, without the user having to define any
statistics-rules for his ontology. Differential sum-
maries can then be used to determine the recent
changes in ontologies, e.g. ”Does the hospital have
a similar allocation of beds, as it had 5 years ago?”.
We emphasize that it is not only intended to use ob-
vious and directly told information on individuals to
create summaries, but to use the locality information
to detect all possibly relevant information.
This article discusses the creation of spatial syn-
opses. For each named individual in the ABox, an
abstraction is computed, given the told ABox infor-
mation. The intuition is that the abstraction corre-
sponds to a subset of the assertional knowledge, rep-
resenting what we know about a given individual and
what is sufficient to perform reasoning with respect
to the given background knowledge. The situation is
depicted in Figure 4.
Figure 4: Semantic summary.
The abstractions for each named individual are
combined, in order to obtain asynopsis/summary of
the whole ontology. In the following, we describe
the formal foundations for computing semantic sum-
maries.
2 DESCRIPTION LOGICS
Description logics are a family of languages for
knowledge representation. Historically, description
logics are descendants of semantic nets (Quillian,
1968) and frame systems (Minsky, 1974). In Artifi-
cial Intelligence, description logics are used for for-
mal reasoning about application domains.
In the following, we recapitulate syntax and se-
mantics of the description logic SH I as far as rele-
vant for this work. Please refer to (Baader, 1999) for
further details. We assume a number of disjoint base
sets as follows: CN is a non-empty set of concept
names, RN is a non-empty set of role names, NIN
is a non-empty set of named individuals, and AIN is
a non-empty set of anonymous individuals. The set
TowardsSemanticSummariesoverOntologies
197

of individuals is IN = NIN ∪ AIN. The set of SH I
-concept descriptions is given by the following gram-
mar:
C
1
, C
2
::=>|⊥|A|¬C
1
|C
1
uC
2
|C
1
tC
2
|∀R.C
1
|∃R.C
1
where A ∈ CN and R ∈ Rol. With AtCon we denote
all atomic concepts, i.e. concept descriptions which
are concept names or negated concept names. For
the semantics of concept descriptions please refer to
(Baader et al., 2007).
A TBox T is a set of so-called generalized con-
cept inclusion axioms C
1
v C
2
. A RBox R is a set
of so-called role inclusion axioms R
1
v R
2
. An ABox
A is a set of so-called concept and role assertion ax-
ioms C(a) and R(a
1
, a
2
). An ontology O consists of
a 3-tuple hT, R, Ai. We restrict the concept assertion
axioms in A in such a way that each concept descrip-
tion is an atomic concept or a negated atomic con-
cept. This is without loss of generality, since each
non-atomic concept description can be given a name
in the TBox. The set of TBoxes (RBoxes, ABoxes,
ontologies) is denoted with ST (SR, SA, SO).
We denote with clos(C) the closure of a concept
description C. The closure of a concept description is
usually used for syntactical analysis. We assume that
a concept description C is usually in negation normal
form, i.e. for all ¬C
1
∈ clos(C), C
1
is a concept name.
Using De Morgan laws, every concept description can
be transformed into a concept description in negation
normal form. The negation normal form of a concept
description C is denoted nn f (C). Given a TBox T, the
concept closure of T, denoted clos(T), is defined as
clos(T) =
[
C
1
vC
2
∈T
(clos(¬C
1
) ∪ clos(C
2
)).
3 INDIVIDUAL ABSTRACTION
In (Wandelt and M
¨
oller, 2008), a method is proposed
to identify the relevant assertions to reason about
an individual. The main motivation is to enable in-
memory reasoning over large ontologies, i.e. ontolo-
gies with a large ABox, for traditional tableau-based
reasoning systems. More formally, given an input in-
dividual a, the proposal is to compute a set of ABox
assertions A
isl
(a subset of the source ABox A), such
that for all atomic (!) concept descriptions C, we have
hT, R, Ai C(a) iff hT, R, A
isl
i C(a).
In order to define subsets of an ABox relevant for
reasoning over an individual a, we define an opera-
tion which splits up role assertions in such a way that
we can apply graph component-based modularization
techniques over the outcome of the split.
ABox
ABox
ann
c1
teaches
ABox split
ABox
ABox
ann
c1
ann*
c1*
teaches
teaches
Figure 5: Intuition of an ABox split.
Definition 1 (ABox Split). Given
• a role description R,
• two distinct named individuals a and b,
• two distinct anonymous individuals c and d, and,
• an ABox A,
an ABox split is a function ↓
R(a,b)
c,d
: SA → SA, defined
as follows:
• If R(a, b) ∈ A and {c, d} * Ind(A), then
↓
R(a,b)
c,d
(A) =A \ {R(a, b)} ∪ {R(a, d), R(c, b)}∪
{C(c) | C(a) ∈ A}∪
{C(d) | C(b) ∈ A}
• Else
↓
R(a,b)
c,d
(A) = A.
The intuition of Definition 1 is depicted in Fig-
ure 5. The clouds in Figure 5 indicate a set of ABox
assertions. We split up a role assertion and keep the
concept assertions for each fresh individual copy. The
reason for keeping the asserted concept descriptions
is explained below. If the ABox does not contain the
role assertion in question, then the split returns an un-
changed ABox.
Definition 2 (Extended ∀-info Structure). Given a
TBox T in normal form and a RBox R, an extended
∀-info structure for T and R is a function extinfo
∀
T,R
:
Rol → ℘(Con), such that we have C ∈ extinfo
∀
T,R
(R)
if and only if there exists a role R
2
∈ Rol, such that
R R v R
2
and ∀R
2
.C ∈ clos(T).
Example 1 (Example for an Extended ∀-info Struc-
ture). Let
T
Ex1
= {
Chair v ∀headO f.Department,
∃memberO f.> v Person,
GraduateStudent v Student
}
KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment
198

Input: Ontology O = hT, R, Ai, individual a ∈
NInd(A)
Output: Individual island ISL
a
= hT, R, A
isl
, ai
Algorithm:
Let agenda = a
Let seen =
/
0
Let A
isl
=
/
0
While agenda 6=
/
0 do
Remove a
1
from agenda
Add a
1
to seen
Let A
isl
= A
isl
∪ {C(a
1
) | C(a
1
) ∈ A}
For each R(a
1
, a
2
) ∈ A
A
isl
= A
isl
∪ {R(a
1
, a
2
) ∈ A}
If R(a
1
, a
2
) ∈ A is S H I -splittable with re-
spect to O then
A
isl
= A
isl
∪ {C(a
2
) | C(a
2
) ∈ A}
else agenda = agenda ∪ ({a
2
} \ seen)
For each R(a
2
, a
1
) ∈ A
A
isl
= A
isl
∪ {R(a
2
, a
1
) ∈ A}
If R(a
2
, a
1
) ∈ A is S H I -splittable with re-
spect to O then
A
isl
= A
isl
∪ {C(a
2
) | C(a
2
) ∈ A}
else agenda = agenda ∪ ({a
2
} \ seen)
Figure 6: Naive algorithm for computation of an individual
island.
and
R
Ex1
= {headO f v memberO f},
then the TBox in normal form is
T
Ex1norm
= {
> v ¬Chair t ∀headO f.Department,
> v ∀memberO f.⊥t Person,
> v ¬GraduateStudent t Student
}
and the extended ∀-info structure for T
Ex1norm
and
R
Ex1
is:
extinfo
∀
T,R
(R) =
{Department, ⊥} if R = headO f,
{⊥} if R = memberO f,
/
0 otherwise.
The extended ∀-info structure allows us to check
which concept descriptions are (worst-case) propa-
gated over role assertions in SH I -ontologies.
Definition 3 (SH I-splittability of Role Assertions).
Given a S H I -ontology O = hT, R, Ai and a role
assertion R(a
1
, a
2
), we say that R(a
1
, a
2
) is SH I -
splittable with respect to O if
1. there exists no transitive role R
2
with respect to R,
such that R R v R
2
,
2. for each C ∈ extinfo
∀
T,R
(R)
• C = ⊥ or
• there exists a concept description C
2
, such that
C
2
(b) ∈ A and T C
2
v C or
• there exists a concept description C
2
, such that
C
2
(b) ∈ A and T C uC
2
v ⊥
and
3. for each C ∈ extinfo
∀
T,R
(R
−
)
• C = ⊥ or
• there exists a concept description C
2
, such that
C
2
(a) ∈ A and T C
2
v C or
• there exists a concept description C
2
, such that
C
2
(a) ∈ A and T C uC
2
v ⊥.
To sum up, for each named individual in the on-
tology, we use the algorithm from Figure 6, to obtain
an abstraction of the individual.
4 SEMANTIC SUMMARIES
Given an individual abstraction for each named indi-
vidual in an input ontology, it is clear that some (or
even many) abstraction are similar to each other. Due
to lack of space we do not go into the technical de-
tails of computing the similarity of individual abstrac-
tion here. However, if one looks at an abstraction as a
graph, graph homomorphisms can be used directly to
determine similar individual islands.
The key insight is that similar abstraction entail
the same set of concept descriptions for there root in-
dividual. Therefore these individuals (of similar ab-
stractions) cannot be distinguished with respect to the
given background knowledge. This is exactly what
we expect from semantic summaries. Thus, for se-
mantic summaries, we propose to look at ontologies
as a set of similar individual abstractions.
We performed some first evaluation of this idea
with respect to a benchmark ontology. The Lehigh
University Benchmark, short LUBM, is a synthetic
ontology developed to benchmark knowledge base
systems with respect to large OWL applications. The
ontology is situated in the university domain. The
background knowledge, i.e. the terminology, is de-
scribed in a schema called Univ-Bench, see (Guo
et al., 2005) for an overview over the history, different
versions and the predecessor Univ 1.0. The expressiv-
ity of the ontology is chosen to be in OWL Lite, which
corresponds to the description logic SH I F . How-
ever, the de facto expressivity is lower. For instance,
TowardsSemanticSummariesoverOntologies
199
the ontology does not introduce any cardinality/func-
tionality expressions on roles.
In Figure 7, we show the number of individu-
als in the dataset, for different numbers of universi-
ties. It can be seen that the number of individuals
increases almost linearly with the number of univer-
sities. Around 30 percent of the individuals in the
dataset are publications, another 30 percent are under-
graduate students, 10 percent are graduate students,
10 percent are courses and graduate courses. The re-
maining 20 percent of the individuals are for instance
professors, assistants and departments. For more de-
tails about the data distribution, see (Guo et al., 2005).
0
500.000
1.000.000
1.500.000
2.000.000
2.500.000
0
20
40
60
80
100
individuals
universities
Figure 7: Number of individuals in LUBM.
Next, we evaluated the number of distinct individ-
ual abstractions for different number of universities.
The result is shown in Figure 8. It can be seen that the
number of distinct individual abstactions is constant -
compared to the linear number of individuals.
Figure 8: Number of distinct individual abstractions for
LUBM.
As a second ontology, we had a look at an ontol-
ogy from the CASAM project. The CASAM project
is focused on computer-aided semantic annotation
of multimedia content. The novelty is the aggrega-
tion of human and machine knowledge. For a de-
tailed discussion of the research objectives, see (Gries
et al., 2010), (Papantoniou et al., 2010), and (Creed
et al., 2010). Within the CASAM project, there is
a need to define an expressive annotation language
which allows for typical-case reasoning systems. The
proposed annotation language is defined by the so-
called Multimedia Content Ontology, short MCO, in-
troduced in (Gries et al., 2009). Inspired by the
MPEG-7 standard, see (ISO/IEC15938-5FCD, 2002),
strictly necessary elements describing the structure of
multimedia documents are extracted. The intention
is to exploit quantitative and qualitative time informa-
tion in order to relate co-occurring observations about
events in videos. Co-occurrences are detected either
within the same or between different modalities, i.e.
text, audio and speech, regarding the video shots.
For our evaluation with respect to MCO, we have
a number of multimedia documents from the CASAM
project. The set of test ontologies contains documents
with identifiers ranging from 1 to 14. Each document
is decomposed into several so-called delta files. Each
delta represents additional information about the doc-
ument of concern. We evaluated our summarization
techniques with respect to all documents. Here we
only show the results for Document 1, since for all
the other documents we obtained very similar statis-
tics.
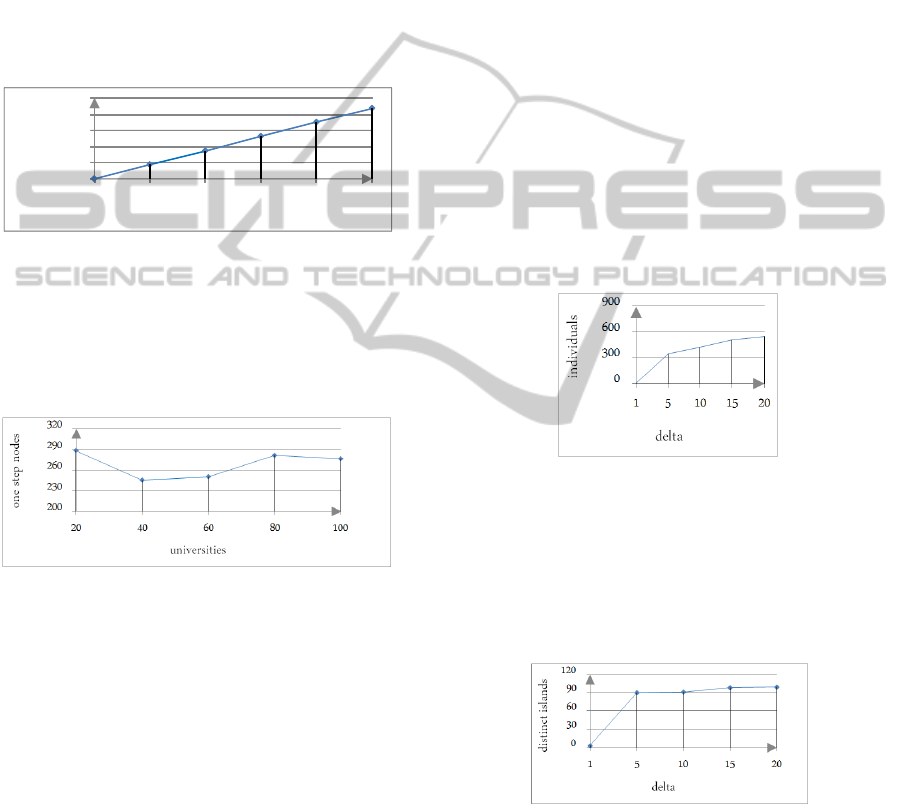
In Figure 9, we show the number of individuals in
the dataset, with an increasing delta. It can be seen
that most individuals are introduced in the first delta
files. The remaining delta files only introduce addi-
tional ABox assertions about already known individ-
uals. Please note that the number of individuals is not
linear in the number of delta.
Figure 9: Number of individuals in Document 1.
We have evaluated the number of individual ab-
stractions for different delta. The result is shown in
Figure 10. It can be seen that the number of dis-
tinct individual abstractions is relatively constant - af-
ter most individuals are introduced in the third and
fourth delta.
Figure 10: Number of distinct individual abstractions for
Document 1.
5 CONCLUSIONS AND FUTURE
WORK
We have proposed first ideas for a notion of seman-
tic summaries that supports industrial information
KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment
200

search scenarios by using (domain specific) industry-
standard vocabularies to query and summarize infor-
mation. It has been shown already that summaries
can be efficiently managed in a distributed computing
setting(Wandelt and M
¨
oller, 2010) and can be used
for reasoning over the ontology of concern (Wandelt
et al., 2010).
For Future Work, we have to evaluate our seman-
tic summary techniques with respect to additional on-
tologies. Furthermore, we would like to formally im-
plement and evaluate difference operators over ontol-
ogy summaries, in order to formally capture ontology
evolution with temporal synopses.
REFERENCES
Baader, F. (1999). Logic-Based Knowledge Representa-
tion. In Artificial Intelligence Today, pages 13–41.
Springer-Verlag.
Baader, F., Calvanese, D., McGuinness, D. L., Nardi, D.,
and Patel-Schneider, P. F. (2007). The Description
Logic Handbook. Cambridge University Press, New
York, NY, USA.
Creed, C., Lonsdale, P., Hendley, R., and Beale, R. (2010).
Synergistic annotation of multimedia content. In Pro-
ceedings of the 2010 Third International Conference
on Advances in Computer-Human Interactions, ACHI
’10, pages 205–208, Washington, DC, USA. IEEE
Computer Society.
Gries, O., M
¨
oller, R., Nafissi, A., Rosenfeld, M., Sokolski,
K., and Wessel, M. (2010). A Probabilistic Abduc-
tion Engine for Media Interpretation Based on Ontolo-
gies. In Hitzler, P. and Lukasiewicz, T., editors, RR,
volume 6333 of Lecture Notes in Computer Science,
pages 182–194. Springer.
Gries, O., M
¨
oller, R., Nafissi, A., Sokolski, K., and Rosen-
feld, M. (2009). CASAM Domain Ontology. Techni-
cal report, Hamburg University of Technology.
Guo, Y., Pan, Z., and Heflin, J. (2005). LUBM: A bench-
mark for OWL knowledge base systems. J. Web Sem.,
3(2-3):158–182.
ISO/IEC15938-5FCD (2002). Multimedia Content
Description Interface (MPEG-7). http://mpeg.
chiariglione.org/standards/mpeg-7/mpeg-7.htm.
Minsky, M. (1974). A Framework for Representing Knowl-
edge. Technical report, MIT-AI Laboratory, Cam-
bridge, MA, USA.
Papantoniou, K., Tsatsaronis, G., and Paliouras, G. (2010).
KDTA: Automated Knowledge-Driven Text Annota-
tion. In Balc
´
azar, J. L., Bonchi, F., Gionis, A., and Se-
bag, M., editors, ECML/PKDD (3), volume 6323 of
Lecture Notes in Computer Science, pages 611–614.
Springer.
Quillian, R. (1968). Semantic memory. In Semantic Infor-
mation Processing, pages 216–270. MIT Press.
Wandelt, S. and M
¨
oller, R. (2008). Island reasoning for
ALCHI ontologies. In Proceedings of the 2008 con-
ference on Formal Ontology in Information Systems,
pages 164–177, Amsterdam, The Netherlands. IOS
Press.
Wandelt, S. and M
¨
oller, R. (2010). Distributed island-based
query answering for expressive ontologies. In Bellav-
ista, P., Chang, R.-S., Chao, H.-C., Lin, S.-F., and
Sloot, P. M. A., editors, GPC, volume 6104 of Lecture
Notes in Computer Science, pages 461–470. Springer.
Wandelt, S., M
¨
oller, R., and Wessel, M. (2010). Towards
scalable instance retrieval over ontologies. Int. J. Soft-
ware and Informatics, 4(3):201–218.
TowardsSemanticSummariesoverOntologies
201
