An Efficient Strategy for Spatio-temporal Data Indexing and Retrieval
Antonio d’Acierno
1
, Marco Leone
2
, Alessia Saggese
2
and Mario Vento
2
1
Institute of Food Sciences, National Research Council, Avellino, Italy
2
Department of Electronic and Information Engineering (DIEII), University of Salerno, Salerno, Italy
Keywords:
Spatio-temporal Queries, Spatio-temporal Data Indexing, Information Retrieval.
Abstract:
Moving people’s and objects’ trajectories extracted from video sequences are increasingly assuming a key role
for detecting anomalous events and for characterizing human behaviors. Among the key related issues, there is
the need of efficiently storing a huge amount of 3D trajectories together with retrieval techniques sufficiently
fast to allow a real-time extraction of trajectories satisfying spatio-temporal requirements. Unfortunately,
while exist well established solutions for 2D trajectories, theoretical solutions proposed for 3D ones are not
widely available in commercial and free spatially enabled DBMS; the paper thus presents a novel method for
extending available 2D indexes to 3D data. In particular, starting from a redundant bi-dimensional indexing
scheme recently introduced in (d’Acierno et al., 2011), we propose a new retrieval system that, while still
using off-the-shelf solutions, avoids almost any redundancy in data to be handled; both the spatial complexity
and the retrieval efficiency for time-interval queries have been significantly improved.
1 INTRODUCTION
In the past decades we have witnessed an increase
in the number of acquisition cameras that represent
a suitable solution for their relative low cost of main-
tenance and the possibility of installing them virtually
everywhere. Once extracted moving objects’ trajecto-
ries by means of video analytic algorithms, these data
need to be efficiently indexed and properly stored, so
to optimize the final retrieval step. Since informa-
tion are usually stored in a database, we will refer to
the retrieval phase as the query processing step. All
the above mentioned steps are far from being simple
tasks: one single video sequence lasting a few hours
can contain thousands of objects of interest, with hun-
dreds of thousands of spatio-temporal displacements.
With regard to the indexing phase, aimed at opti-
mizing the retrieval operation, a widely adopted so-
lution for bidimensional problems is represented by
R-trees (Guttman, 1984), which hierarchically orga-
nize geometric data representing each object using
its Minimum Bounding Rectangle (MBR). Starting
from Guttman’s pioneering paper, many other index-
ing schemes have been proposed, most of which opti-
mize and extend R-trees to the 3D space.
(Pfoser et al., 2000), for instance, capture and in-
dex trajectory data by using STR-tree and TB-tree,
while SEB-trees have been adopted by (Song and
Roussopoulos, 2003) in order to segment trajecto-
ries with respect to space and time. Another index-
ing scheme based on R-trees, recently introduced by
(Priyadarshini et al., 2011), is R k-d trie tree, which
is able to reduce the time complexity. (Chakka et al.,
2003) present a R*-tree based indexing scheme called
SETI, which is demonstratedoutperforming the three-
dimensional R-tree; SETI’s basic idea is to partition
the space and use R*-tree on each of these parti-
tions in order to build a sparse time index. (Park
et al., 2010) present IsGrid, a grid-based indexing
scheme, which provides better performance by avoid-
ing some unnecessary visits while descending the in-
dexing structure. Other indexing structures, proposed
by (Zheng, 2011), are TPR-tree and an optimized ver-
sion of it, namely FT-tree (Full Temporal tree). As for
the low-level storage optimization, TrajStore (Cudre-
Mauroux et al., 2010) aims at minimizing the number
of disk accesses by co-locating on a disk block (or in
a collection of near blocks) trajectory segments and
by using an adaptive multi-level grid; thanks to this
method, it is possible to retrieve the desired informa-
tion by only reading a few blocks.
All the above approaches, even presenting effi-
cient solutions from different perspectives, typically
are not widely supported both in commercial and
freely available products; for instance, PostGIS (Obe
and Hsu, 2011), the well known extension of Post-
greSQL DBMS for storing spatial data, while sup-
porting three (and four)-dimensional data, does not
227
d’Acierno A., Leone M., Saggese A. and Vento M..
An Efficient Strategy for Spatio-temporal Data Indexing and Retrieval.
DOI: 10.5220/0004137102270232
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2012), pages 227-232
ISBN: 978-989-8565-29-7
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

support three-dimensional intersection and indexing
operations. As a consequence, there is a strong inter-
est in those methods which, even using off-the-shelf
solutions, allow to solve the problem in the three-
dimensional space.
In (d’Acierno et al., 2011), problems related to
3D data are solved by means of a redundant storing
method that, at the extent of an increased spatial com-
plexity, allows to index data using widely available
bidimensional strategies. In this paper we propose
a system that, even still using well-established bidi-
mensional indexes, substantially avoids any redun-
dancy in the stored data; the resulting querying time,
moreover, is substantially decreased when compared
to (d’Acierno et al., 2011) even thanks to a segmen-
tation algorithm aimed at optimizing the use of the
adopted indexes.
2 THE PROPOSED METHOD
A three dimensional trajectory is usually referred to
as a sequence of spatio-temporal points:
T
i
=< P
i
1
, P
i
2
, ..., P
i
N
>
where the generic point P
i
k
= (x
i
k
, y
i
k
,t
i
k
) represents the
spatial location (x
i
k
, y
i
k
) of an object at the time instant
t
i
k
. From now on, we will use the line segments model
(Pfoser et al., 2000), each segment being the line con-
necting two consecutive points.
0
0
0
x
max
x
x
min
y
min
y
y
max
t
t
s
t
e
Figure 1: A query box representing a TIQ.
A trajectory-based time interval query (TIQ) aims
at detecting all those objects’ trajectories passing
through a given spatial area in a given time interval.
Here, we think to the area as a rectangle with coordi-
nates (x
min
, y
min
) and (x
max
, y
max
) while [t
s
,t
e
] are the
starting and final time instants. According to this as-
sumption, each TIQ can be associated to a query box
B (Figure 1), which identifies the spatio-temporal vol-
ume possibly containing the trajectories.
To solve a TIQ, we have to verify, for each tra-
jectory, if at least one of its segments intersects the
query box. The intersection between a segment and
a box can be verified by using a clipping algorithm,
a well-known family of algorithms widely used for
identifying the portion of an image which is either
outside or inside a picture. One of the most effi-
cient is the Cohen-Sutherland Line Clipping Algo-
rithm (Newman and Sproull, 1979), which works, in
its 3D formulation, by subdividing the plane into 27
regions by extending the faces of the query box.
However, despite its simplicity, the use of a
clipping algorithm is not suited for handling large
datasets: in fact, in the worst case, arising when a
trajectory does not intersect the query box, all the
trajectory’ segments must be processed, making this
approach unfeasible for a large amount of trajectory
data. It means that, in real applications, it is necessary
to make use of more efficient approaches, as the ones
using suitable indexing strategies, known as spatial
indexing. Spatial indexes allow to efficiently perform
queries involving geometry data types such as points,
lines and polygons; a query in this case represents a
spatial relationship among these geometric entities.
In the 3D space, given a trajectory T
k
and a query
box B, it is straightforward to observe that, if T
k
inter-
sects B, then the projection of T
k
on each coordinate
plane also intersects the correspondentquery box pro-
jection; this of course represents a necessary but not
sufficient condition, as the opposite is clearly not true.
Thus, if all projections of T
k
intersect the correspon-
dent box projections, we suggest to consider T
k
as a
candidate to be clipped in the 3D space.
According to the above considerations, in
(d’Acierno et al., 2011), for each 3D trajectory T
k
,
we proposed to store three 2D trajectories obtained
by projecting T
k
on the xy plane (T
k
xy
), on the xt plane
(T
k
xt
) and on the yt plane (T
k
yt
). Given a box B repre-
senting the time interval query to be solved, we sim-
ilarly considered B
xy
, B
xt
and B
yt
. By using one of
the available bidimensional indexes, it is possible to
efficiently find, on each coordinate plane kz, the set:
Θ
kz
= {T
kz
: MBR(T
kz
) ∩B
kz
6=
/
0} (1)
The set Θ of trajectories to be clipped in the 3D space
is thus trivially defined as:
Θ = {T : T
xy
∈ Θ
xy
∧ T
xt
∈ Θ
xt
∧ Θ
yt
∈ T
yt
} (2)
This strategy, while taking advantage of widely
available efficient bidimensional indexes, still
presents two weak points. First, for a n points
trajectory, we need to redundantly store 6 · n values
(2·n for each of the three coordinate planes). Another
subtle crucial point is that the use of bidimensional
indexes is not optimized: as a matter of fact, the
MBR of each projected trajectory can easily span a
great percentage of the whole area.
KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
228

It is possible to observe that, for a given trajec-
tory T
k
, rather than storing the three different tra-
jectory projections in each coordinate plane, we can
store T
k
as the original sequence of points in the
3D space, and separately maintain three different
bidimensional MBRs: MBR
xy
(T
k
), MBR
xt
(T
k
) and
MBR
yt
(T
k
). MBR
xy
(T
k
) (respectively MBR
xt
(T
k
)
and MBR
yt
(T
k
)) is obtained by projecting on the xy
(respectively xt and yt) plane the 3D MBR of T
k
.
It is worth noting that the redundancy introduced
by the three MBR projections is not dependent on
the number of points in the trajectory and, therefore,
has only a marginal impact on the spatial complexity,
since it only requires the storage of six pairs of points.
Assuming such a scheme, on each 2D plane we
find the trajectories intersecting the corresponding 2D
query box in a very efficient manner by using one of
the available 2D indexes. Let Γ
xy
, Γ
xt
and Γ
yt
be three
sets of trajectories, each one defined as:
Γ
kz
= {T : MBR
kz
(T) ∩ B
kz
6=
/
0} (3)
where, as usual, B
xy
, B
xt
and B
yt
are the projections
of the 3D query box B. The set Θ of the trajectories
candidate to be clipped in the 3D space is therefore
now defined as:
Θ = Γ
xy
∩ Γ
xt
∩ Γ
yt
(4)
It should be clear at this point that the entire sys-
tem performancewill strongly depend on the indexing
phase and, as a consequence, on the capability to re-
duce the number of trajectories to be clipped in the
three-dimensional space. At a more detailed analysis,
the selectivity of the indexes in each plane is related
to the area of the corresponding MBR which, in turn,
only depends on the trajectory geometry,so being (ap-
parently) fixed. This is the reason why we decided to
introduce a segmentation stage, aimed at increasing
the selectivity of the indexes.
Segmentation aims at subdividing each trajectory
into consecutive smaller units, which we will refer
to as trajectory units. The proposed algorithm aims
at exploiting the characteristics of the available bidi-
mensional indexes by decreasing the area of the pro-
jected MBRs of each trajectory unit by recursively
working. Initially (that is at iteration 0), it assumes
that the trajectory T
k
is composed by a single unit
0
U
k
1
, that is split into a set of m consecutive smaller
units {
1
U
k
1
, . . . ,
1
U
k
m
}; each of the
1
U
k
i
is in turn in-
spected and, if the stop criteria are not satisfied, it is
further split.
Let us analyze how a generic unit
(i−1)
U
j
=
{P
1
, . . . , P
m
} is split into {
i
U
1
, . . . ,
i
U
n
}; we first
choose a split-dimension (sd) and a split-value (s
∗
).
Assume, as an example and without loss of generality,
that x has been chosen as the split-dimension and let
x
∗
be the split-value. In addition, assume that x
1
< x
∗
.
According to these hypotheses,
i
U
1
is the set of the
consecutive points lying on the left side of x
∗
:
i
U
1
= {P
1
, . . . , P
k
} (5)
where P
k
is thus the first point such that x
k
≥ x
∗
. Then,
the second unit will be formed by the sequence of con-
secutive points lying on the right side of x
∗
:
i
U
2
= {P
k+1
, . . . , P
l
} (6)
where P
l
is the first point such that x
k
≤ x
∗
. The in-
spection of
(i−1)
U ends when P
m
is reached.
According to the above considerations, the criteria
for the choice of sd and s
∗
play a crucial role. Since
we aim at optimizing the indexing strategy, the pro-
posed segmentation algorithm is based on the occu-
pancy percentage on each 2D coordinate plane. Thus,
with reference to the generic unit
i
U
j
to be segmented,
we calculate the three occupancy percentage values
O
xy
, O
xt
and O
yt
of as follows
1
:
O
kz
=
A(MBR
kz
(
i
U
j
))
A(V
kz
)
(7)
Without loss of generality, suppose that the maximum
occupancy percentage value is O
xy
and, consequently,
the corresponding plane is xy; let W and H be the two
dimensions of MBR
xy
(
i
U
j
), respectively along the co-
ordinates x and y; sd is defined as x if (W > H) and
as y otherwise. Given sd, s
∗
is the MBR
kz
’s average
point on the coordinate sd.
The algorithm ends when all the trajectory units
cannot be further subdivided, since at least one of
the stop conditions has been reached for each unit;
in particular, we employ two stop criteria . First,
we only segment units composed by more than PS
min
points. Furthermore, we choose not to segment trajec-
tory units whose MBR areas are smaller than a fixed
percentage of the entire scenario (PA
min
).
3 EXPERIMENTAL RESULTS
To validate the effectiveness of the proposed method,
we tested our system performing several TIQs. The
database has been implemented by storing the trajec-
tories’ data in Postgres using PostGIS; data are in-
dexed using the standard bidimensional R-tree over
GiST (Generalized Search Trees) indexes since the
specialized literature highlights that this choice guar-
antees higher performance in case of spatial queries,
1
A(·) indicates the area while V
kz
represents the projec-
tion of the volume of interest on the coordinate plane kz.
AnEfficientStrategyforSpatio-temporalDataIndexingandRetrieval
229

if compared with the PostGIS implementation of R-
trees.
We represent each trajectory’s unit as a tuple:
(ID,UID,U
xyt
, MBR
xy
, MBR
xt
, MBR
yt
)
where ID is the moving objects identifier, UID iden-
tifies the trajectory’s unit, and U
xyt
is the 3D trajec-
tory unit, represented as a sequence of segments (a
PostGIS 3D multi-line). Finally, MBR
xy
, MBR
xt
, and
MBR
yt
are the three unit’s MBRs in each coordinate
plane, represented as PostGis BOX geometries. Once
data have been indexed, PostGIS provides a very effi-
cient function to perform intersections between boxes
and MBRs in a 2D space. We conducted our experi-
ments on a PC equipped with an Intel quad core CPU
running at 2.66 GHz, using the 32 bit version of the
PostgreSQL 9.1 server and the 1.5 version of Post-
GIS.
We tested our information retrieval system with
synthetic data, which have been generated as follows.
Let W
S
and H
S
be the width and the height of our
scene and I be the time interval we are interested in.
Each trajectory starting point is randomly chosen in
our scene at a random time instant t
1
; the trajectory
length L is assumed to be fixed while the initial direc-
tions along the x axis and the y axis, respectively d
x
and d
y
, are randomly chosen. At each time step t, we
first generate the new direction, assuming that d
x
and
d
y
can vary with probability PI
x
and PI
y
respectively;
subsequently, we randomly chose the velocity along
x and y. The velocity is expressed in pixels/seconds
and is assumed to be greater than 0 and less than two
fixed maxima, V
max
x
and V
max
y
. Therefore the new po-
sition of the object can be easily derived; if it does
not belong to our scene, new values for d
x
and/or d
y
are generated. We refer to the scene populated with
trajectories as the Scenario. Table 1 reports the free
parameters and the values for the creation of the 25
different scenarios used in our experiments as well as
the parameters used to constrain the number of seg-
ments in each trajectory. Note that the worst case,
corresponding to the maximum values of L and of the
number of trajectories T, results in 10
4
trajectories
with 10
4
points, for a total of 10
8
points to be stored
and processed; this value is over and above the size of
many real world datasets publicly available.
The time needed to process a generic TIQ query
(QT) is a function of many parameters, since it surely
depends on the number of trajectories T, on the tra-
jectory length L, on the query cube dimension D
c
(ex-
pressed as percentage of the volume V = W
S
∗ H
S
∗ I),
and on the position of the query box P
c
.
In particular, P
c
strongly influences the time
needed to extract the trajectories as, in real world sce-
narios, the trajectories are not uniformly distributed.
Table 1: The parameters used in our experiments.
W
S
(pixels) 10
4
H
S
(pixels) 10
4
I (seconds) 10
5
T {1, 2,3, 5, 10}∗ 10
3
L {1, 2,3, 5, 10}∗ 10
3
PI
x
5%
PI
y
5%
V
max
x
(pixels/secs) 10
V
max
y
(pixels/secs) 10
PA
min
1%
PS
min
300
To avoid the dependence on the query cube position,
we decided to repeat the query a number of times in-
versely proportional to the query cube dimension, as
shown in row N of Table 2; finally, results are aver-
aged to obtain:
QT = f(T, L, D
c
). (8)
For the description of the experimental results on our
data, we propose three different set of experiments
obtained fixing two of the three parameters T, L and
D
c
, and showing the variation of QT with respect to
the third (free) parameter.
Table 2: Number N of times each query is repeated as D
c
varies.
D
c
1% 5% 10% 20% 30% 50%
N 200 40 20 10 7 4
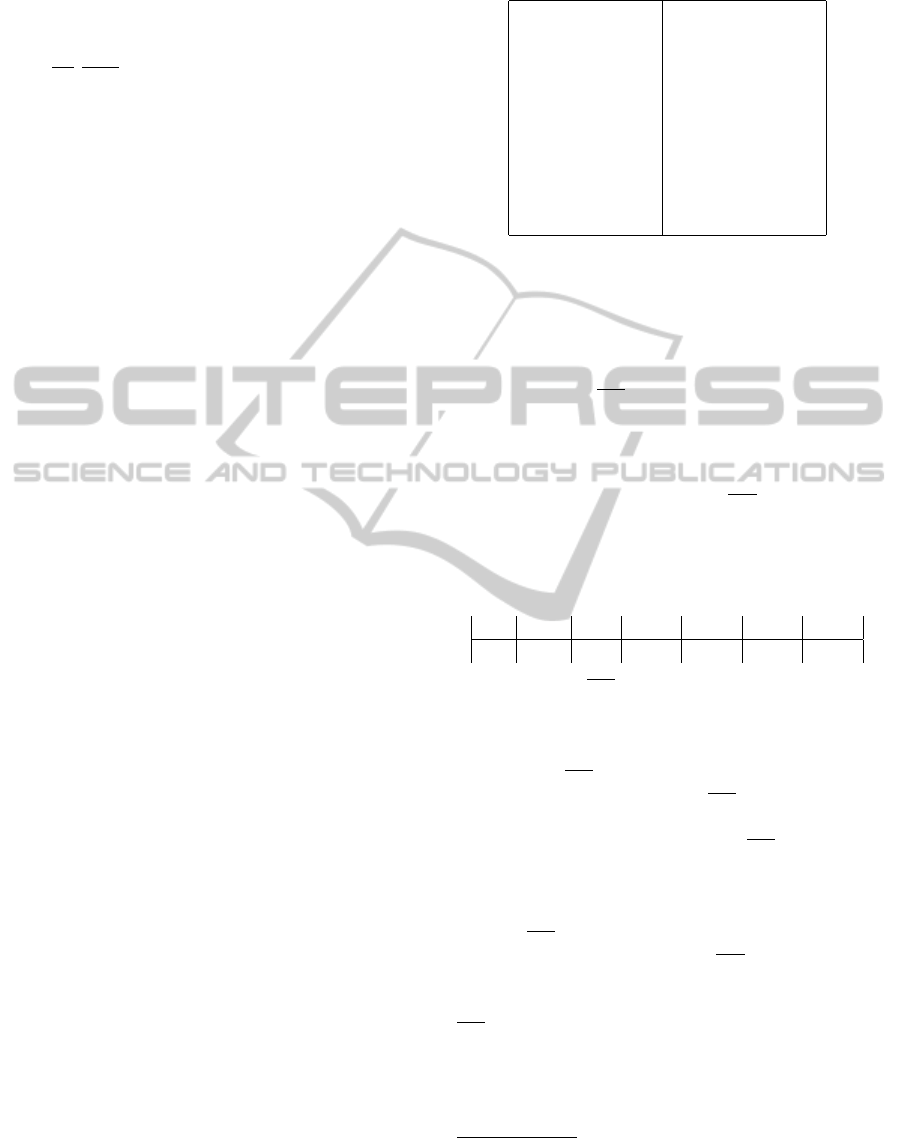
In Figure 2, QT is related to the variable number
of trajectories T, both for small (D
c
= 5%) and large
(D
c
= 30%) query boxes; the number of curves corre-
sponds to the different fixed values of L. The relation-
ship between QT and T has been analyzed by polyno-
mially approximating QT(T): QT linearly increases
with T with a very small factor of approximation
2
.
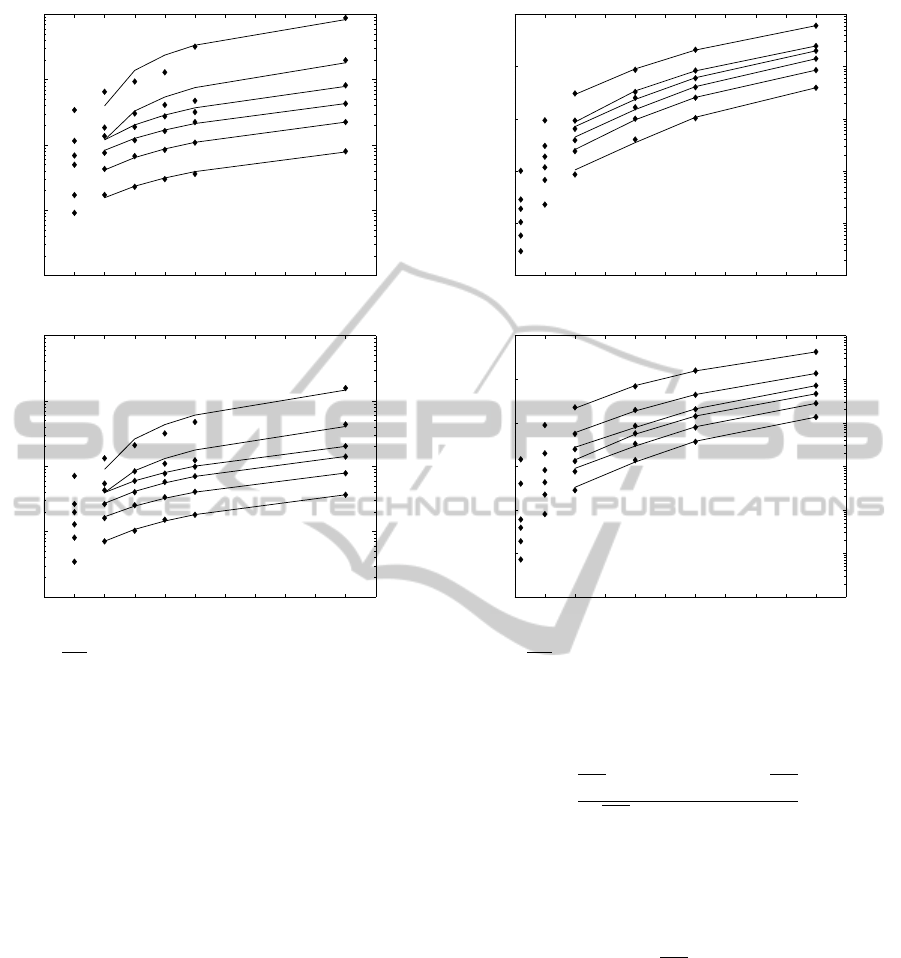
Diamond points in Figure 3 express QT in relation to
the query box dimensions D
c
and for T = 3.000 and
T = 10.000 (the number of curves again corresponds
to the different fixed values of L). In this case we ob-
tain that QT quadratically depends on D
c
. Finally, in
Figure 4 the diamonds express QT as a function of
L, for D
c
= 5% and D
c
= 30%, while the number of
curves corresponds to the different fixed values of T:
QT increases quadratically with L.
2
The semi-log scale provides a greater comprehension
of the system behavior for large values of the parameters,
even not permitting to display some of the lines interpolat-
ing small values.
KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
230

1000 5000 10000
10
−3
10
−2
10
−1
10
0
10
1
D
c
= 5%
1000 5000 10000
10
−1
10
0
10
1
10
2
10
3
D
c
= 30%
Figure 2: QT (in seconds) as T increases having L as pa-
rameter.
4 CONCLUSIONS
Motivated by the fact that many of the existing solu-
tions to index 3D data are not widely available both
in commercial and freely available products, we are
investigating the possibility of using widely available
2D indexes to deal with 3D data, and, in this paper,
we propose a possible solution.
Our strategy has been implemented using PostGIS
and the experimental results, obtained on TIQs per-
formed on synthetic data, show that, even thanks to
a segmentation algorithm we have proposed, the ob-
tained system is able to fully exploit retrieving capa-
bilities based on well established 2D indexes.
Our solution evolves the method presented
in (d’Acierno et al., 2011), where the indexing of
3D data through bidimensional structures has been
obtained using a redundant storing scheme. Spatial
complexity, in fact, has been improved through the
removal of almost any redundancy in the data to be
stored. For what concerns the time complexity, while
a careful theoretical analysis is outside the scope of
5 10 20 30 50
10
−3
10
−2
10
−1
10
0
10
1
10
2
T = 3000
5 10 20 30 50
10
−3
10
−2
10
−1
10
0
10
1
10
2
10
3
T = 10000
Figure 3: QT (in seconds) as D
c
(in percentage of the whole
volume) increases and having L as parameter.
this paper, it is possible to empirically define the im-
provement index η as follows:
η =
QT
(d
′
Aciernoet al.,2011)
− QT
QT
(d
′
Aciernoet al.,2011)
(9)
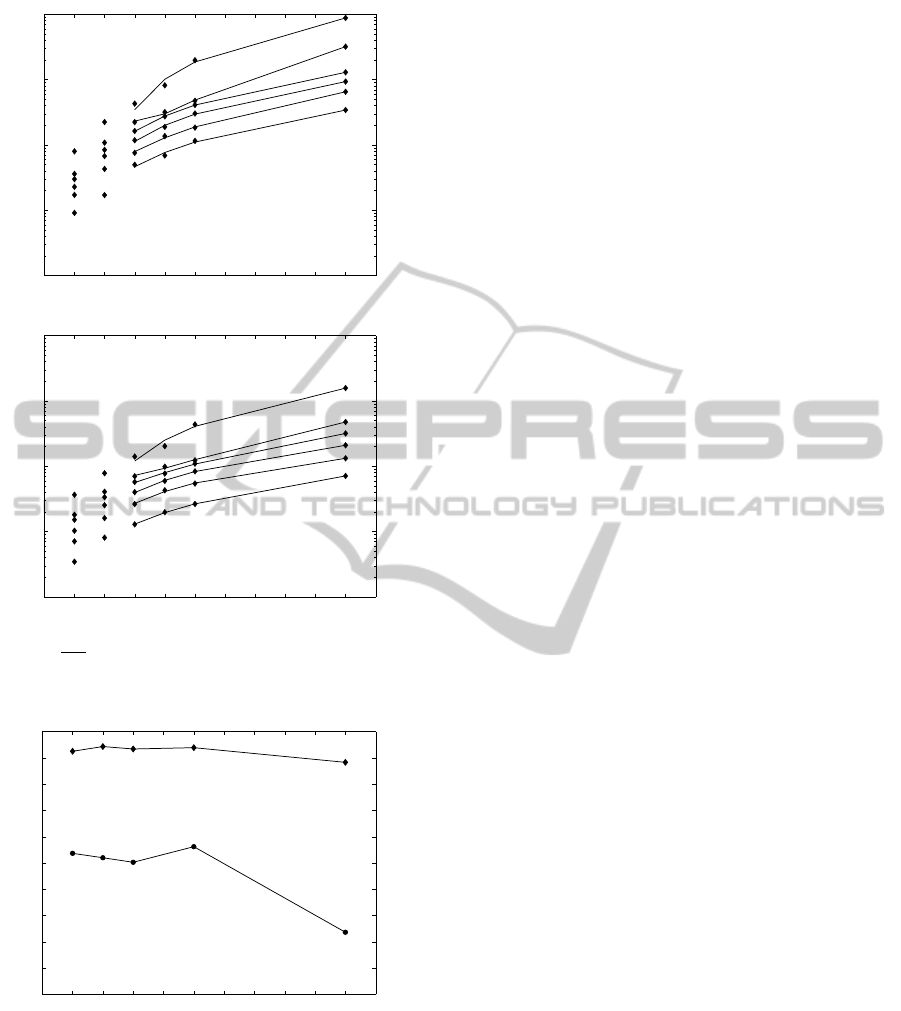
Figure 5 shows η as T increases (with L = 5000) for
small query cubes (DC = 5%, diamonds) as well as
for big query cubes (DC = 30%, circles). There is a
significant improvement for small query cubes and an
interesting improvement for large cubes. Intuitively,
this is due to the fact that QT is lower bounded by the
time needed to extract trajectories.
Further improvements in the performance will be
hopefully achieved first of all by applying the clip-
ping algorithm in parallel to each candidate trajectory
to take advantage of multi-core and multi-processors
systems. To reduce the extraction time, strategies
aiming at compressing data to be stored and retrieved
are also being considered. Moreover, we are extend-
ing our system in order to answer different query ty-
pologies as well as to handle multi-dimensional data.
AnEfficientStrategyforSpatio-temporalDataIndexingandRetrieval
231

1000 5000 10000
10
−3
10
−2
10
−1
10
0
10
1
D
c
= 5%
1000 5000 10000
10
−1
10
0
10
1
10
2
10
3
D
c
= 30%
Figure 4: QT (in seconds) as L increases and having T as
parameter.
1000 5000 10000
0
10
20
30
40
50
60
70
80
90
100
Figure 5: η as T increases for DC = 5% (diamonds) and
DC=30% (circles) (L = 5000).
ACKNOWLEDGEMENTS
This research has been partially supported by
A.I.Tech s.r.l. (a spin-off company of the Univer-
sity of Salerno, www.aitech-solutions.eu) and by the
FLAGSHIP InterOmics project (PB.P05, funded and
supported by the Italian MIUR and CNR organiza-
tions).
REFERENCES
Chakka, V. P., Everspaugh, A., and Patel, J. M. (2003). In-
dexing large trajectory data sets with seti. In First
Biennial Conference on Innovative Data Systems Re-
search (CIDR 2003), Asilomar, CA, USA.
Cudre-Mauroux, P., Wu, E., and Madden, S. (2010). Tra-
jstore: An adaptive storage system for very large tra-
jectory data sets. In Int. Conf. on Data Engineering,
pages 109–120, Los Alamitos, CA, USA. IEEE CS.
d’Acierno, A., Saggese, A., and Vento, M. (2011). A re-
dundant bi-dimensional indexing scheme for three-
dimensional trajectories. In Proc. of the 1th Conf.
on Advances in Information Mining and Management
(IMMM11), pages 73–78, Barcelona, Spain.
Guttman, A. (1984). R-trees: a dynamic index structure for
spatial searching. In Proc. of ACM SIGMOD Confer-
ence, pages 47–57, New York, NY, USA. ACM.
Newman and Sproull (1979). Principles of interactive com-
puter graphics. Mc Graw-Hill, Singapore, 2nd edi-
tion.
Obe, R. and Hsu, L. (2011). PostGIS in Action. Manning
Publications Co., Greenwich, CT, USA.
Park, Y., Seo, D., Lim, J., Lee, J., Kim, M., Bao, W., Ryu,
C. T., and Yoo, J. (2010). A new spatial index structure
for efficient query processing in location based ser-
vices. In Proc.of the 2010 IEEE Int. Conf. on Sensor
Networks, Ubiquitous, and Trustworthy Computing,
SUTC ’10, pages 434–441, Washington, DC, USA.
IEEE Computer Society.
Pfoser, D., Jensen, C. S., and Theodoridis, Y. (2000). Novel
approaches in query processing for moving object tra-
jectories. In Proc. of VLDB Conf., pages 395–406, San
Francisco, CA, USA. Morgan Kaufmann Publ. Inc.
Priyadarshini, J., AnandhaKumar, P., Aparna, M., Geetha,
J., and Shobana, N. (2011). Indexing and querying
technique for dynamic location updates using r k-d
trajectory trie tree. In Int. Conf. on Recent Trends in
Information Technology (ICRTIT), pages 1143 –1148.
Song, Z. and Roussopoulos, N. (2003). Seb-tree: An ap-
proach to index continuously moving objects. In Pro-
ceedings of the 4th International Conference on Mo-
bile Data Management, MDM ’03, pages 340–344,
London, UK, UK. Springer-Verlag.
Zheng, Y. (2011). A fast index method for moving objects
on full temporal query. In 3rd Int. Conf. on Com-
puter Research and Development (ICCRD), volume 3,
pages 205 –208.
KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
232