
Prototypes Vs Exemplars in Concept Representation
Marcello Frixione
1
and Antonio Lieto
2
1
DAFIST, University of Genova, Genoa, Italy
2
Computer Science Department, University of Turin, Turin, Italy
Keywords: Concept Representation, Formal Ontologies, Non Classical Concepts, Psychological Theories of Concepts,
Typicality Effects, Conceptual Spaces.
Abstract: Concept representation is still an open problem in the field of ontology engineering and, more in general, of
knowledge representation. In particular, it still remains unsolved the problem of representing "non classical"
concepts, i.e. concepts that cannot be defined in terms of necessary and sufficient conditions. In this paper
we review empirical evidence from cognitive psychology, which suggests that concept representation is not
an unitary phenomenon. In particular, it seems that human beings employ both prototype and exemplar
based representations in order to represent non classical concepts. We suggest that a similar, hybrid
prototype-exemplar based approach could be useful also in the field of formal ontology technology.
1 INTRODUCTION
This article deals with the problem of representing
non classical concepts in formal ontologies. By non
classical concepts we mean concepts that cannot be
represented in terms of sets of necessary and/or
sufficient conditions. After introducing the problem
(sect. 2), we review some empirical evidence from
cognitive psychology, which suggests that concept
representation is not an unitary phenomenon (sect.
3). In particular, prototype and exemplar based
models of non classical concepts are both plausible,
and can account for different aspects of human
abilities. In sect. 4 we argue that these results could
suggest the adoption of a hybrid approach in the
field of formal ontologies; in sect. 5 we sketch the
proposal of an architecture for concept
representation based on both prototypes and
exemplars. Some concluding remarks follow (sect.
6).
2 REPRESENTING NON
CLASSICAL CONCEPTS
The representation of common sense concepts is still
an open problem in ontology engineering and, more
in general, in Knowledge Representation (KR) (see
e.g. Frixione and Lieto, in press). Cognitive Science
showed the empirical inadequacy of the so-called
“classical” theory of concepts, according to which
concepts should be defined in terms of sets of
necessary and sufficient conditions. Rather, Eleanor
Rosch’s experiments (Rosch, 1975) – historically
preceded by the philosophical analyses by Ludwig
Wittgenstein (Wittgenstein, 1953) – showed that
ordinary concepts can be characterized in terms of
prototypical information.
These results influenced the early researches in
knowledge representation: the KR practitioners
initially tried to keep into account the suggestions
coming from cognitive psychology, and designed
artificial systems – such as frames and early
semantic networks – able to represent concepts in
“non classical” (prototypical) terms (for early KR
developments, see Brachman and Levesque, 1985).
However, these early systems lacked clear
formal semantics and a satisfactory meta-theoretic
account, and were later sacrificed in favour of a
class of formalisms stemmed from the so-called
structured inheritance semantic networks and the
KL-ONE system (Brachman and Schmoltze, 1985).
These formalisms are known today as description
logics (DLs, Baader et al., 2010). DLs are logical
formalisms, which can be studied by means of
traditional, rigorous metatheoretic techniques
developed by logicians. However, they do not allow
exceptions to inheritance, and the possibility to
represent concepts in prototypical terms. From this
point of view, therefore, such formalisms can be
seen as a revival of the classical theory of concepts.
226
Frixione M. and Lieto A..
Prototypes Vs Exemplars in Concept Representation.
DOI: 10.5220/0004139102260232
In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2012), pages 226-232
ISBN: 978-989-8565-30-3
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

As far as prototypical information is concerned, such
formalisms offer only two possibilities: representing
it resorting to tricks or ad hoc solutions, or,
alternatively, ignoring it. For obvious reasons, the
first solution in unsuitable: it could have disastrous
consequences for the soundness of the knowledge
base and for the performances of the entire system.
The second choice severely reduces the expressive
power of the representation. For example, in
information retrieval terms, this could severely
affect the system's recall. Let us suppose that you are
interested in documents about flying animals. A
document about birds is likely to interest you,
because most birds are able to fly. However, flying
is not a necessary condition to being a bird (there are
many birds that are unable to fly). So, the fact that
birds usually fly cannot be represented in a
formalism that allows only the representation of
concepts in classical terms, and the documents about
birds will be ignored by your query.
Nowadays, DLs are widely adopted within many
fields of application, in particular within the area of
ontology representation. For example, OWL is a
formalism in this tradition, which has been endorsed
by the World Wide Web Consortium for the
development of the Semantic Web. However, DL
formalisms leave unsolved the problems of
representing concepts in prototypical terms.
Within the field of logic oriented KR, rigorous
approaches exist, designed to make it possible the
representation of exceptions, and that therefore are,
at least in principle, suitable for dealing with (some
aspects of) “non-classical” concepts. Examples are
fuzzy and non-monotonic logics. Therefore, the
adoption of logic oriented semantics is not
necessarily incompatible with the representation of
prototypical effects. Various fuzzy and non-
monotonic extensions of DL formalisms have been
proposed. Nevertheless, such approaches pose
various theoretical and practical problems, which in
part remain unsolved (see Frixione and Lieto, 2010
for a discussion).
As a possible way out, we outline here a tentative
proposal that goes in a different direction, and that is
based on some suggestions coming from empirical
cognitive science research. Within the field of
cognitive psychology, different positions and
theories on the nature of concepts are available; all
of them are assumed to account for (some aspects
of) prototypical effects in conceptualisation (see e.g.
Murphy, 2002 and Machery, 2009). Here we shall
take into account two of such approaches, namely
prototypes and the so-called exemplar view.
According to the prototype view, knowledge
about categories is stored in terms of prototypes, i.e.
in terms of some representation of the “best”
instances of the category. For example, the concept
CAT should coincide with a representation of a
prototypical cat. In the simpler versions of this
approach, prototypes are represented as (possibly
weighted) lists of features.
According to the exemplar view, a given
category is mentally represented as set of specific
exemplars explicitly stored within memory: the
mental representation of the concept CAT is the set
of the representations of (some of) the cats we
encountered during our lifetime.
These approaches turned out to be not mutually
exclusive. Rather, they seem to succeed in
explaining different classes of cognitive phenomena,
and many researchers hold that all of them are
needed to explain psychological data (see again
Murphy, 2002 and Machery, 2009). In this
perspective, we propose to integrate some of them in
computational representations of concepts.
Prototype and exemplar based approaches to
concept representation are, as mentioned above, not
mutually exclusive, and they succeed in explaining
different phenomena. Exemplar based
representations can be useful in many situations.
According to various experiments, it can happen that
instances of a concept that are rather dissimilar from
the prototype, but are very close to a known
exemplar, are categorized quickly and with high
confidence. For example, a penguin is rather
dissimilar from the prototype of BIRD. However, if
we already know an exemplar of penguin, and if we
know that it is an instance of BIRD, it is easier for us
to classify a new penguin as a BIRD. This is
particularly relevant for concepts (such as
FURNITURE, or VEHICLE) whose members differ
significantly from one another.
Exemplar based representations are easier and
faster to acquire, when compared to prototypes. In
some situations, it can happen that there is not
enough time to extract a prototype from the
available information. Moreover, the exemplar based
approach makes the acquisition of concepts that are
not linearly separable easier (see Medin and
Schwanenflugel, 1981). In the following section we
shall review some of the available empirical
evidence concerning prototype and exemplar based
approaches to concept representation in psychology.
PrototypesVsExemplarsinConceptRepresentation
227

3 EXEMPLARS VS.
PROTOTYPES IN COGNITIVE
PSYCHOLOGY
As anticipated in the previous section, according to
the experimental evidence, exemplar models are in
many cases more successful than prototypes.
Consider the so-called “old-items advantage effect”.
It consists in the fact that already known items are
usually more easily categorized than new items that
are equally typical (see Smith and Minda, 1998 for a
review). For example: it is easier for me to classify
my old pet Fido as a dog (even supposing that he is
strongly atypical) than an unknown dog with the
same degree of typicality. This effect is not
predicted by prototype theories. Prototype
approaches assume that people abstract a prototype
from the stimuli presented during the learning phase,
and categorize old as well as new stimuli by
comparing them to it. What matters for
categorization is the typicality degree of the items,
not whether they are already known or not. By
contrast, the old-item advantage is banal to explain
in the terms of the exemplar paradigm.
This is correlated to a further kind of empirical
evidence in favour of exemplar theories. It can
happen that a less typical item can be categorized
more quickly and more accurately than a more
typical category member if it is similar to previously
encountered exemplars of the category (Medin and
Schaffer, 1978). Consider the penguin example
mentioned in the previous section: a penguin is a
rather atypical bird. However, let us suppose that
some exemplar of penguin is already stored in my
memory as an instance of the concept BIRD. In this
case, it can happen that I classify new penguins as
birds more quickly and more confidently than less
atypical birds (such as, say, toucans or
hummingbirds) that I never encountered before.
Linearly separable
categories
Non linearly separable
categories
Figure 1: Linearly separable and non separable categories.
Another important source of evidence for the
exemplar model stems from the study of linear
separable categories (see, again, Medin and
Schwanenflugel, 1981). Two categories are linearly
separable if and only if it is possible to determine to
which of them an item belongs by summing the
evidence concerning each attribute of this item. For
example, let us suppose that two categories are
characterized by two attributes, or dimensions,
corresponding to the axes in fig. 1. These categories
are linearly separable if and only if the category
membership of each item can be determined by
summing its value along the x and y axes, or, in
other terms, if a line can be drawn, which separates
the members of the categories.
According to the prototype approach, people
should find it more difficult to form a concept of a
non-linearly separable category. Subjects should be
faster at learning two categories that are linearly
separable. However, Medin and Schwanenflugel
(1981) experimentally proved that categories that are
not linearly separable are not necessarily harder to
learn. This is not a problem for exemplar based
theories, which do not predict that subjects would be
better at learning linearly separable categories. In the
psychological literature, this result has been
considered as a strong piece of evidence in favour of
the exemplar models of concept learning.
The above mentioned results seem to favour
exemplars against prototypes. However, other data
do not confirm this conclusion. Moreover, it has
been argued that many experiments favourable to the
exemplar approach rest on a limited type of
evidence, because in various experimental tasks a
very similar category structure has been employed
(Smith and Minda, 2000). Nowadays, it is
commonly accepted that prototype and exemplars
are not competing, mutually exclusive alternatives.
In fact, these two hypotheses can collaborate in
explaining different aspects of human conceptual
abilities (see e.g. Murphy, 2002 and Machery,
2009).
An empirical research supporting the hypothesis
of a multiple mental representation of categories is
in Malt (1989). This study was aimed to establish if
people categorize and learn categories using
exemplars or prototypes. The empirical data,
consisting in behavioral measures such as
categorization probability and reaction time, suggest
that subjects use different strategies to categorize.
Some use exemplars, a few rely on prototypes, and
others appeal to both exemplars and prototypes. A
protocol analysis of subjects’ descriptions of the
adopted categorization strategy confirms this
interpretation (a protocol analysis consists in
recording what the subjects of an experiment say
after the experiment about the way in which they
performed the assigned tasks). Malt (1989) writes:
KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment
228

"Three said they used only general features of
the category in classifying the new exemplars. Nine
said they used only similarity to old exemplars, and
eight said that they used a mixture of category
features and similarity to old exemplars. If reports
accurately reflect the strategies used, then the data
are composed of responses involving several
different decision processes” (p. 546-547).
These findings are consistent with other well
known studies, such as Smith et al. (1997) and Smith
and Minda (1998). Smith et al. (1997) found that the
performances of half of the subjects of their
experiments best fitted the prototype hypothesis,
while the performances of the other half were best
explained by an exemplar model. Therefore, it is
plausible that people can learn at least two different
types of representation for concepts, and that they
can follow at least two different strategies of
categorization. Smith and Minda (1998) replicated
these findings and, additionally, found that during
the learning, subjects’ performances are best fitted
by different models according to the features of the
category (e.g., its dimensions) and the phase of the
learning process, suggesting that when learning to
categorize artificial stimuli, subjects can switch from
a strategy involving prototypes to a strategy
involving exemplars. They also found that the
learning path is influenced by the properties of the
learned categories. For example, categories with
few, dissimilar members favour the use of exemplar-
based categorization strategies. Thus, psychological
evidence suggests that, in different cases, we employ
different categorization mechanisms.
Summing up, prototype and exemplar
approaches present significant differences, and have
different merits. We conclude this section with a
brief summary of such differences. First of all,
exemplar-based models assume that the same
representations are involved in such different tasks
as identification (e.g., “this is the Tower Bridge”)
and categorization (Nosofsky, 1986). This contrasts
with prototype models, which assumes that these
tasks involve different kinds of representations.
Furthermore, prototype representations synthetically
capture only some central, and cognitively relevant,
aspects of a category, while models based on
exemplars are more analytical, and represent in toto
the available knowledge concerning the instances of
a given category.
This is related to another aspect of divergence,
which pertains the categorization process. Both
prototype and exemplar models assume that the
similarity between prototypical/exemplar
representations and target representations is
computed. The decision of whether the target
belongs to some category depends on the result of
this comparison. However, important differences
exist. According to the prototype view, the
computation of similarity is usually assumed to be
linear. Indeed, since prototypes are synthetic
representations, all information stored in them is
relevant. Therefore, if some property is shared by
the target and by some prototype, this is sufficient to
increase the similarity between them, independently
from the fact that other properties are shared or not.
On the contrary, an exemplar based representation
includes information that is not relevant from this
point of view (typically, information that
idiosyncratically concerns specific individuals). As a
consequence, the computation of similarity is
assumed to be non-linear: an attribute that is shared
by the target and by some exemplar is considered to
be relevant only if other properties are also shared.
Prototypes and exemplar based approaches
involve also different assumptions concerning
processing and memory costs. According to the
exemplar models, a category is mentally represented
by storing in our long term memory many
representations of category members; according to
prototype theorists, only some parameters are stored,
which summarize the features of a typical
representative of the category. As a consequence, on
the one hand, prototypes are synthetic
representations that occupy a smaller memory space.
On the other hand, the process of creating a
prototype requires more time and computational
effort if compared to the mere storage of knowledge
about exemplars, which is computationally more
parsimonious, since no abstraction is needed.
4 HYBRID
PROTOTYPE-EXEMPLAR
REPRESENTATIONS
Given the evidence presented in the above section, it
is likely, in our opinion, that a dual, prototype and
exemplar based, representation of concepts could
turn out to be useful for the representation of non
classical concepts in ontological knowledge bases
also from a technological point of view.
In the first place, there are kinds of concepts that
seem to be more suited to be represented in terms of
exemplars, and concepts that seem to be more suited
to be represented in terms of prototypes. For
example, in the case of concepts with a small
number of instances, which are very different from
one another, a representation in terms of exemplars
PrototypesVsExemplarsinConceptRepresentation
229
should be more convenient. An exemplar based
representation could be more suitable also for non
linearly separable concepts (see the previous
section).
On the other hand, for concepts with a large
number of very similar instances, a representation
based on prototypes seems to be more appropriate.
Consider for example an artificial system that deals
with apples (for example a fruit picking robot, or a
system for the management of a fruit and vegetable
market). Since it is no likely that a definition based
on necessary/sufficient conditions is available or
adequate for the concept APPLE, then the system
must incorporate some form of representation that
exhibits typicality effects. But probably an exemplar
based representation is not convenient in this case:
the systems has to do with thousands of apples,
which are all very similar one another. A prototype
would be a much more natural solution.
In many cases, the presence of both a prototype
and an exemplar based representation seems to be
appropriate. Let us consider the concept BIRD. And
let us suppose that a certain number of individuals
b
1
, …., b
n
are known by the systems to be instances
of BIRD (i.e., the system knows for sure that b
1
, ….,
b
n
are birds). Let us suppose also that one of these
b
i
's (say, b
k
) is a penguin.
Then, a prototype P
BIRD
is extracted from
exemplars b
1
, …., b
n
, and it is associated with the
concept BIRD. Exemplar b
k
concurs to the
extraction of the prototype, but, since penguins are
rather atypical birds, it will result to be rather
dissimilar from P
BIRD
. Let us suppose now that a
new exemplar b
h
of penguin must be categorized. If
the categorization process were based only on the
comparison between the target and the prototype,
then b
h
(which in its turn is rather dissimilar from
P
BIRD
) would be categorized as a bird only with a
low degree of confidence, in spite of the fact that
penguins are birds in all respects. On the other hand,
let us suppose that the process of categorization
takes advantage also of a comparison with known
exemplars. In this case, b
h
, due to its high degree of
similarity to b
k
, will be categorized as a bird with
full confidence. Therefore, even if a prototype for a
given concept is available, knowledge of specific
exemplars should be valuable in many tasks
involving conceptual knowledge. On the other hand,
the prototype should be useful in many other
situations.
5 A HYBRID
PROTOTYPE-EXEMPLAR
ARCHITECTURE
In this section we outline the proposal of a possible
architecture for concept representation, which takes
advantage of the suggestions presented in the
sections above. It is based on a hybrid approach, and
combines a component based on a Description Logic
(DL) with a further component that implements
prototypical representations.
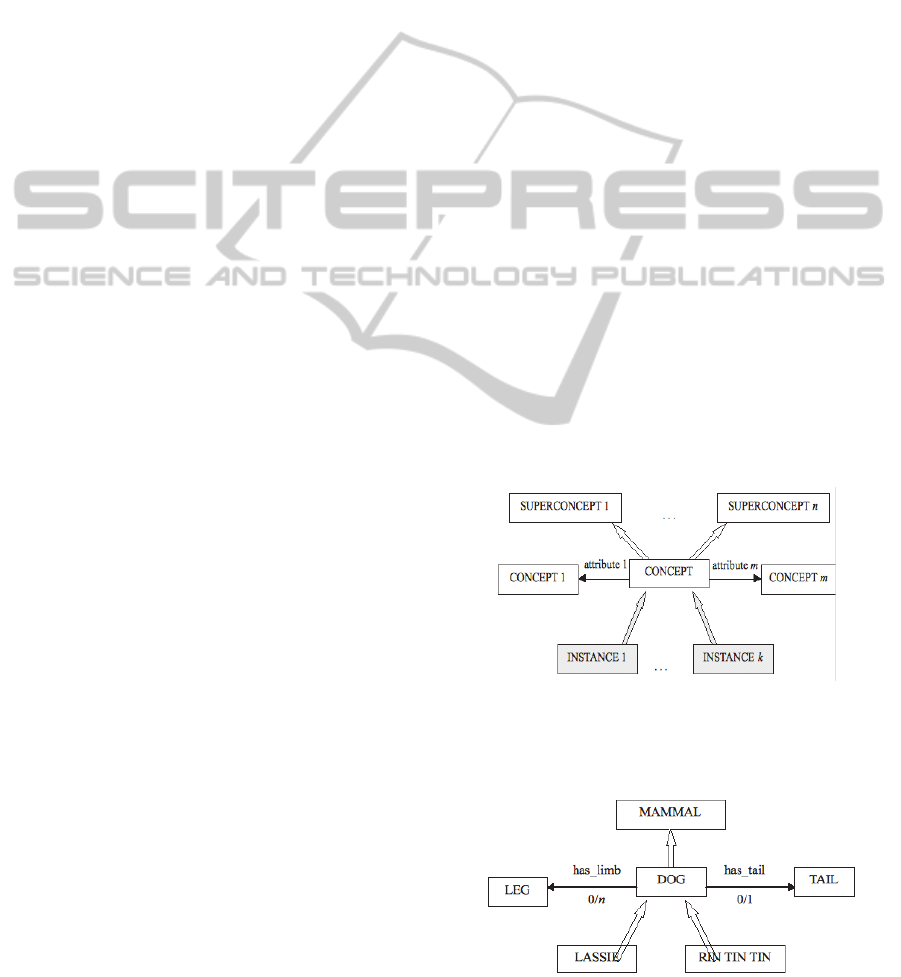
Concepts in the DL component are represented
as in fig. 2. As usual, every concept can be
subsumed by a certain number of superconcepts, and
it can be characterised by means of a number of
attributes, which relate it to other concepts in the
knowledge base. Restrictions on the number of
possible fillers can be associated to each attribute.
Given a concept, its attributes and its
concept/superconcept relations express necessary
conditions for it. DL formalisms make it possible to
specify which of these necessary conditions also
count as sufficient conditions.
Since in this component only
necessary/sufficient condition can be expressed, here
concepts can be represented only in classical terms:
no exceptions and no prototypical effects are
allowed. Concepts can have any number of
individual instances, that are represented as
individual concepts in the taxonomy.
Figure 2: A concept in the DL component.
As an example, consider the fragment of network
shown in fig. 3.
Figure 3: An example of concept.
KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment
230

Here the concept DOG is represented as a
subconcept of MAMMAL. Since DL networks can
express only necessary and/or sufficient conditions,
some details of the representation are very loose. For
example, according to fig. 3, a DOG may or may not
have a tail (this is the expressed by the number
restriction 0/1 imposed on the attribute has_tail),
and has an unspecified number of limbs (since some
dogs could have lost limbs, and teratological dogs
could have more than four legs). LASSIE and RIN
TIN TIN are represented as individual instances of
DOG (of course, concepts describing individual
instances can be further detailed, fully specifying for
example the values of the attributes inherited from
parent concepts).
Prototypes describing typical instances of
concepts are represented as data structures that are
external to the DL knowledge base. Such structures
could, for example, be lists of (possibly weighted)
attribute/value pairs that are linked to the
corresponding concept. Some attributes of the list
should correspond to attributes of the DL concept,
which value can be further specified at this level.
For example, the prototypical dog is described as
having a tail, and exactly four legs. Other attributes
of the prototype could have no counterpart in the
corresponding DL concept.
As far as the exemplar-based component of the
representations is concerned, exemplars are directly
represented in the DL knowledge base as instances
of concepts. (It may also happen that some
information concerning exemplars is represented
outside the DL component, in the form of Linked
Data. Typically, this could be the case of “non
symbolic” information, such as images, sounds,
etc.).
It must be noted that prototypical information
about concepts (either stored in the form of
prototypes or extracted from the representation of
exemplars) extends the information coded within the
DL formalism. The semantic network provides
necessary and/or sufficient conditions for the
application of concepts, as a consequence, such
conditions hold for every instance of concepts, and
cannot be violated by any specific exemplar. So,
what can be inferred on the basis of prototypical
knowledge can extend, but can in no way conflict
with what can be deduced from the DL based
component.
6 CONCLUSIONS
In conclusion, we assume that a hybrid
prototype/exemplar based representation of non
classical concepts could make ontological
representation of common-sense concepts more
flexible and realistic, thus avoiding at the same time
some frequent misuses of DL formalisms.
As a further development of the work presented
here, we are currently investigating the possibility of
adopting conceptual spaces (Gärdenfors, 2000) as an
adequate framework for representing both
prototypes and exemplars in many different
contexts. Gärdenfors (2004) and others (Adams and
Raubal, 2009) proposed conceptual spaces as a tool
for representing knowledge in the semantic web.
From our point of view, conceptual spaces could
offer a common, computational framework do
develop our proposal of representing concepts in
terms of both prototypes and exemplars.
REFERENCES
Adams B., and Raubal M., 2009. The Conceptual Space
Markup Language (CSML): Towards the Cognitive
Semantic Web. 3
rd
IEEE Int. Conf. on Semantic
Computing (ICSC 2009), Berkeley, CA, 253-260.
Baader F., D. Calvanese, D. McGuinness, D. Nardi, P.
Patel-Schneider, 2010. The Description Logic
Handbook, 2
nd
edition, CP, Cambridge, UK.
Brachman R., Levesque, H. (eds.), 1985. Readings in
Knowledge Representation, Morgan Kaufmann, Los
Altos, CA.
Brachman R., J. G. Schmolze, 1985. An overview of the
KL-ONE knowledge representation system, Cognitive
Science 9, 171-216.
Frixione, M., Lieto, A., 1910. The Computational
Representation of Concepts in Formal Ontologies:
Some General Consideration, Proc. KEOD 2010,
Valencia, Spain, 396-403.
Frixione, M., Lieto, A., in press. Representing Concepts in
Formal Ontologies: Compositionality vs. Typicality
Effects, to appear in Logic and Logical Philosophy.
Gärdenfors, P., 2000. Conceptual Spaces: The Geometry
of Thought. The MIT Press, Cambridge, MA.
Gärdenfors, P. 2004. How to make the Semantic Web
more Semantic. Proc. 3rd Int. Conf. on Formal
Ontology in Inf. Syst. (FOIS), Torino, Italy.
Machery E., 2009. Doing without Concepts. Oxford
University Press, Oxford.
Malt B. C., 1989. An on-line investigation of prototype
and exemplar strategies in classification. J. Exp. Psyc.:
Learning, Memory, and Cognition 15(4), 539-555.
Medin D. L., Schaffer M. M., 1978. Context theory of
classification learning. Psychol. Rev. 85(3), 207-238.
Medin D. L., Schwanenflugel P. J., 1981. Linear
separability in classification learning. J. Exp. Psyc.:
Human Learning and Memory 7, 355-368.
Murphy G. L., 2002. The Big Book of Concepts. The MIT
Press, Cambridge, MA.
Nosofsky R. M., 1986. Attention, similarity, and the
PrototypesVsExemplarsinConceptRepresentation
231

identification categorization relationship. J. Exp.
Psychology: General, 115, 39-57.
Rosch E., 1975. Cognitive representation of semantic
categories, J. Exp. Psychology, 104, 573-605.
Smith J. D., Minda J. P., 1998. Prototypes in the mist: The
early epochs of category learning. J. Exp. Psyc.:
Learning, Memory, & Cognition 24, 1411-1436.
Smith J. D., Minda J. P., 2000. Thirty categorization
results in search of a model. J. Exp. Psyc.: Learning,
Memory, and Cognition, 26, 3-27.
Smith J. D., Murray M. J., J. P. Minda, 1997. Straight talk
about linear separability. J. Exp. Psyc.: Learning,
Memory, and Cognition, 23, 659-68.
Wittgenstein L., 1953. Philosophische Untersuchungen,
Blackwell, Oxford, UK.
KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment
232
