FuzzyAlign

A Fuzzy Method for Ontology Alignment

Susel Fernández, Juan R. Velasco, Ivan Marsa-Maestre and Miguel A. Lopez-Carmona

Department of Computer Engineering, University of Alcalá, Alcalá de Henares, Madrid, Spain

Keywords: Semantic Web, Ontology Mapping, Fuzzy Systems, Machine Learning.

Abstract: The need of sharing information and services makes data integration as one of the most requested issues in

the Semantic Web. Ontologies are crucial for formally specifying the vocabulary and the concepts within a

domain, so, for better interoperability is important to translate data from one ontological framework to

another. Ontology matching is the process of finding correspondences between the concepts of different

ontologies. This problem is being addressed in many studies but has not managed to automate the matching

process fully considering all the complex structure of the ontologies. This paper aims to provide

mechanisms to support experts in the ontology matching process by using fuzzy logic techniques to

determine the similarity between entities from different ontologies. We propose FuzzyAlign, a Multi-Layer

fuzzy rule-based system, which obtains the alignments by taking into account both the lexical and semantic

elements of names, and the relational and the internal structures of the ontologies to obtain the alignments.

The ideas presented in this work were validated using the OAEI evaluation tests for ontology alignment

systems in which we have obtained good results.

1 INTRODUCTION

AND RELATED WORKS

At the present time the exchange of information and

services through the Web is increasingly necessary.

Due to its high degree of expressiveness the use of

ontologies are more and more widespread to

increase the interoperability in the semantic Web.

However, services produced by different developers

may use different or partially overlapping sets of

ontologies, so it is necessary to translate data from

one ontological framework to another. Ontology

matching is needed for the exchange of information

and services within the Semantic Web, finding

correspondences between the concepts of different

ontologies. The mapping or alignment should be

expressed by some rules that explain this

correspondence.

There are some previous works aimed at

ontology alignment, which have made interesting

contributions, but so far none offers a complete

matching due to the structural complexity of the

ontologies.

SMART (Noy and Musen, 1999), PROMPT

(Noy and Musen, 2003) and PROMPTDIFF (Noy

and Musen, 2002) are tools that have been

developed using linguistic similarity matches

between concepts and a set of heuristics to identify

further matches.

Other developments use probabilistic methods,

such as CODI (Noessner et al., 2010) that produces

mappings between concepts, properties, and

individuals. The system is based on the syntax and

semantics of Markov logic. GLUE (Doan et al.,

2004) employs machine learning techniques to find

mappings. In (Pan et al., 2005) a probabilistic

framework for automatic ontology mapping based

on Bayesian Networks is proposed. This approach

only takes into account the probability of occurrence

of concepts in the web, which makes it fail if two

very similar concepts have not the same level of

popularity.

There are more recent works that combine

lexical similarity with other techniques, one of them

is ASMOV (Jean-Mary et al., 2009), which

iteratively calculates the similarity by analyzing

lexical elements, relational structure, and internal

structure.

AgreementMaker (Cruz et al., 2009) comprises

several matching algorithms that can be concept-

based or structural. The concept-based matchers

support the comparison of strings and the structural

matchers include the descendants’ similarity

Fernández S., Velasco J., Marsa-Maestre I. and A. Lopez-Carmona M..

FuzzyAlign - A Fuzzy Method for Ontology Alignment.

DOI: 10.5220/0004139500980107

In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2012), pages 98-107

ISBN: 978-989-8565-30-3

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

inheritance.

In Eff2Match (Watson Wey et al., 2010) the

alignment process consists of four stages: Anchor

Generation, where entities are identified using an

exact string matching technique; Candidates

Generation, where they find for entities using a

vector space model approach; Anchor Expansion, to

identifies more equivalent pairs of entities using

terminological methods and Iterative Score Boosting

to identify more pairs of equivalent concepts using

the expanded anchor set.

GeRMeSMB (Quix et al., 2010) is the

integration of two tools; GeRoMeSuite offers a

variety of matchers which can match ontologies and

schemas in other modelling languages such as XML

or SQL; and SMB mainly works on the similarity

matrices produced by GeRoMeSuite. It improves the

clarity of the similarity values by reinforcing ‘good’

values and penalizing ‘bad’ values for increase the

precision of the match result.

SOBOM (Xu et al., 2010) deals with ontology

from two different perspectives: ontology with

hierarchical structure and ontology with other

relationships, combining the results of every step in

a sequential way. If the ontologies have regular

literals and hierarchical structures, the system can

achieve satisfactory alignments and avoid missing

alignment in many partitioning matching methods. If

the literals of concept missed, the system will get

bad results.

Our proposal focuses on the first steps of

ontology matching, using fuzzy logic techniques to

find similarities between entities, taking into account

lexical and semantic elements of names, and both

relational and internal structure of ontologies. Due to

the combination of linguistic methods with semantic

and evolutive learning on a significant number of

test ontologies we have obtained very accurate

alignments in general purpose ontologies,

outperforming most of the existing methods.

The rest of the paper is organized as follows:

Section 2 describe the main ontology elements; Then

we discuss the similarity measures. Section 4

presents the fuzzy rule-based system; Section 5 and

6 are dedicated to the evaluation measures and the

experimental results respectively. Finally the last

section summarizes our conclusions and enumerates

some future lines of research.

2 ONTOLOGY ELEMENTS

Ontology provides a common vocabulary of an area

and defines the meaning of the terms and relations

between them in different levels of formality. The

components of ontologies are classes (concepts),

relations, axioms and individuals. The classes or

concepts in the ontology represent any entity that

provides some information and contain properties.

Relations represent interactions between classes.

Among the most common relations we can find is

inheritance, which is usually called taxonomic.

Taxonomy is a class hierarchy, where each class is

also called node. Axioms are used to define the

meaning of ontological components, and individuals

are concrete instances of a particular class. So far

most of the existing systems for ontology matching

have focused primarily on calculating similarities

between the names of concepts, and properties, but

there are few studies that exploit the hierarchical

structure of classes. In the same way, to our

knowledge no process focuses on axioms and

individuals because many ontologies do not have.

3 SIMILARITY MEASURES

In this section we define our proposed similarity

measurements. These are the both semantic and

linguistic similarities (Fernández et al., 2009) and

the structural similarity, using the taxonomy of the

ontologies and the internal structure of the concepts

properties.

3.1 Semantic Similarity

The semantic similarity is calculated using the

Jaccard coefficient (Rijsberguen, 1979) that is one of

the most used binary similarity indexes. Given two

sets of data this coefficient is defined as the size of

the intersection divided by the size of the union. For

two observations i and j, the Jaccard coefficient is

calculated by:

abc





(1)

where a is the number of times that both

observations have the value 1, b is the number of

times observation i has value 1 and observation j has

value 0, and c is the number of times observation i

has value 0 and observation j has value 1.

For the semantic similarity calculation we make

successive searches of documents from the web,

specifically in (Wikipedia). In a similar way to (Pan

et al., 2005), to ensure that the search only returns

relevant documents to the entities, the search query

is formed by combining all the terms on the path

from the root to the current node in the taxonomy.

FuzzyAlign-AFuzzyMethodforOntologyAlignment

Let us assume that the set A

contains the elements

that support entity A, and the set A

contains the

elements that support the negation of A. Elements in

are obtained by searching for pages that contain

A and all A’s ancestors in the taxonomy, while

elements of A

would be those where A’s ancestors

are present but not A. For each pair of entities A and

B, three different counts are made (a) the size of

∩B

, (b) the size of A

∩B

, and (c) the size of

∩A

. Once these values are obtained for each pair

of origin and destination ontology entities their

similarity is calculated using Equation 1. For

example, if we get the semantic similarity between

concepts Book and Proceedings in the ontologies

shown in Figure 1 would be formed following

search queries:

Query(A

∩B

)=“Library”+”Publication”+

”Book”+ “Conference”+”Proceedings”.

Query(A

∩B

)=“Library”+”Publication”+”Book”+

“Conference”-”Proceedings”.

Query(B

∩A

)=“Conference”+”Proceedings”+

“Library”+”Publication”-”Book”.

Finally applying Equation 1, the semantic

similarity of these two concepts would be 0.21.

Figure 1: Parts of two ontologies for semantic similarity.

3.2 Lexical Similarity

The lexical is the strongest indicator of similarity

between entities, because usually the ontology

developers within the same domain use linguistically

related terms to express equivalent entities

(Fernández et al., 2009). In this work two types of

lexical similarity are calculated: one based on the

synonyms, and another based on the derivationally

related forms of the words. Given the concepts A

and B, the first step is to remove the meaningless

words (stop words), and then obtain lists of

synonyms and words derived from each one using

WordNet (Fellbaum, 1998).

Next, we apply the Porter stemming algorithm

(Porter, 1980) to remove the morphological ends of

the words from the lists of synonyms and derivated

words. Let L

and L

be the lists of roots obtained in

the previous step, we calculate the two lexical

similarities as the intersection of the two lists

(Equation 2):

min ,















(2)

where c

is the number of words in the list L

that are on L

, c

is the number of words in the list

that are in L

, T

is the total number of words in

the list L

, and T

is the total number of words in the

list L

3.3 Structural Similarity

The structural similarity among the entities in

ontologies is bases on two key issues: the relational

structure, which consider the taxonomic hierarchy of

concepts; and the internal structure, comprising

property restrictions of concepts.

3.3.1 Hierarchical Similarity

For the relational structure similarity, we rely on the

taxonomic hierarchy. We define the “extra”

similarity as the influence that the siblings, parents

and descendants have on the final similarity of

concepts.

We start from the idea that if two concepts A and

B are similar, and their siblings, descendants, or

parents are also similar, it is likely that A and B are

equivalents.

Figure 2 shows an example of how to calculate the

“extra” similarity of siblings. Let m be the number of

siblings of the concept A, n the number of siblings of

the concept B and let A

and B

be the i

and j

siblings of concepts A and B, respectively. The

“extra” similarity would be the average of the

maximum of the similarities between all the siblings

of A and all of B (Equation 3).



max ( , )

extra i j

Sim sim A B





(3)

Figure 2: ”Extra” similarity of the concepts A and B based

on the similarity of their siblings.

3.3.2 Property Similarity

This work also considers the internal structure of the

entities for their similarity. To do this we compute

the similarity between the properties. The similarity

between two properties is influenced by three

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

100

factors: the similarity of the classes to which they

belong (domain), the lexical similarity of their

names and the similarity of their types (range).

We consider two types of properties: Object

Properties and Data Properties. In the case of the

Object Properties because they are instances of

another class, the range similarity is directly the

similarity between those classes, while in the case of

Data Properties, being specific data (the range is its

data type), we calculate the similarities between

their data types, so we have defined an equivalence

data type table.

3.4 Improvement of Similarity

The improvement of the similarities between classes

is to use the similarities of properties to enhance or

decrease the value of the final similarity. Thus we

start from the principles that if two classes have

some degree of similarity, they have the same

number of properties and these properties are

similar, we probably dealing with the same or

equivalent classes, so we increase their similarity.

In contrast, if two classes have some

resemblance, but they have not the same number of

properties or these properties are not similar, we

decrease their similarity value. For each pair of

classes A and B we call “extra” similarity of

property to the value they bring to the final class

similarity. It is calculated as the same way as in the

taxonomic hierarchy (Equation 3).

4 A MULTI-LAYER FUZZY

RULE-BASED SYSTEM

Fuzzy Rule-based Systems constitute an extension to

classical rule-based systems. They deal with "IF-

THEN" rules whose antecedents and consequents

are composed of fuzzy logic statements instead of

classical logic ones. They have been successfully

applied to a wide range of problems in different

domains with uncertainty and incomplete knowledge

(Cordon et al., 2001). A Fuzzy Rule-based System

consists of 4 parts: the knowledge base; the

inference engine that is responsible for drawing the

conclusions from the symbolic data that have arrived

using the rules governing the system in which it

works; and the fuzzification and defuzzification

interfaces which have the function of converting a

crisp input values in a fuzzy values and the other

way around.

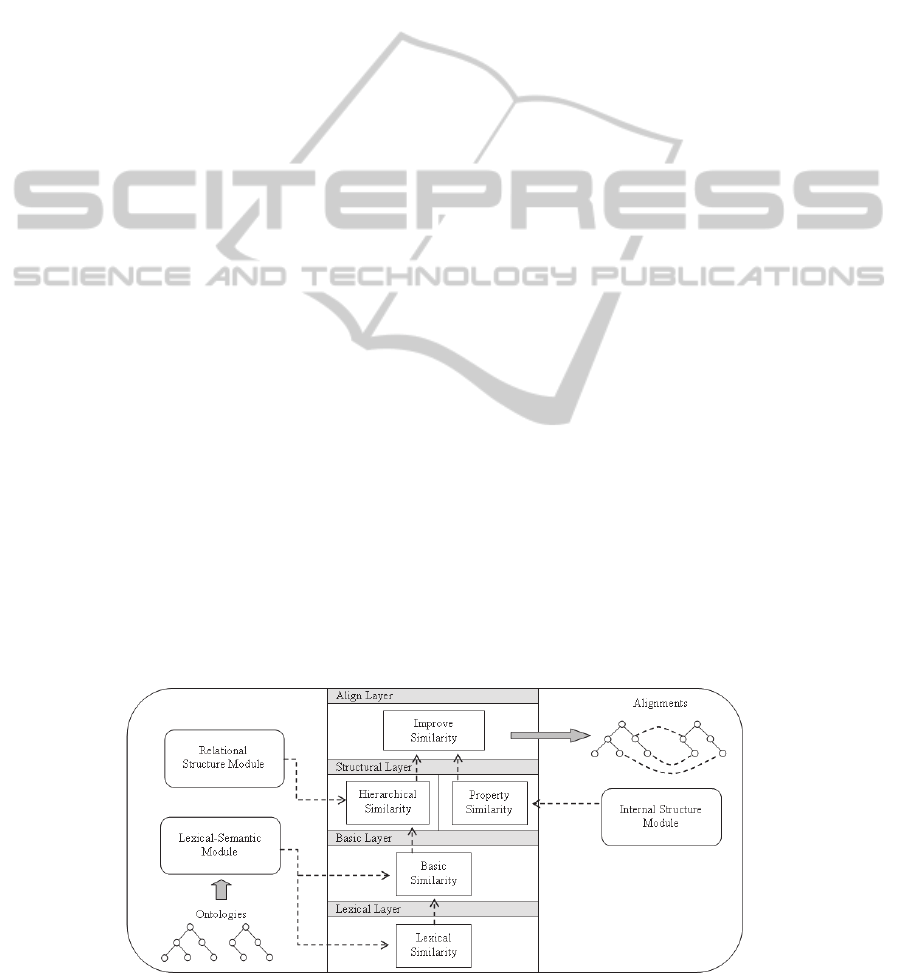
We defined FuzzyAlign, a multi-layer fuzzy

rule-based system. The system is composed by four

layers. The output values of each one serves as input

to the upper layer and each layer provides an

improvement in the calculation of the similarity: the

first one is the lexical similarity layer, the second

one is the basic similarity layer, the third is the

structural layer and the latter is the align layer.

Figure 3 shows the architecture of the system.

4.1 Lexical Layer

In the first layer of the fuzzy system, to calculate the

lexical similarity the two input variables represent

the similarities of synonyms and derivations,

respectively, and the output variable represents the

overall linguistic similarity. To achieve this we use

the Lexical-Semantic module, where lexical

similarities are calculated in the manner explained in

Section 3.2 using WordNet.

The three variables have the following linguistic

terms: D

ling

= {Low(L), Regular(R), Medium(M),

High(H), Very High(VH)}. Because of the

distribution of lexical similarity values, equally

spaced fuzzy sets were defined. The triangular

membership functions are shown in Figure 4.

Figure 3: Architecture of FuzzyAlign.

FuzzyAlign-AFuzzyMethodforOntologyAlignment

101

Figure 4: Fuzzy triangular-shaped membership functions

for linguistic similarity variables.

4.2 Basic Layer

In the second layer of the fuzzy system we defined

two input variables and one output to calculate the

basic similarity of the concepts. These variables are:

Sim_Jaccard: This input variable represents the

semantic similarity. The value of semantic similarity

is calculated in the Lexical-Semantic module using

the Jaccard coefficient on the results of successive

searches of the concepts on the web as explained in

Section 3.1. It uses the following linguistic terms:

jacc

= {Low(L), Regular(R), Medium(M), High(H),

Very High(VH)}. To define the membership

functions, it was first necessary to divide the values

into groups, so we use the quartiles of the data to

narrow the membership triangles as follows: Low: (-

0.00224168, 0, 0.00224168), Regular: (0,

0.00224168, 0.03031929), Medium: (0.00224168,

0.03031929, 0.10712543), High: (0.03031929,

0.10712543, 1), Very High: (0.10712543, 1,

1.10712543).. Membership functions are shown in

Figure 5(a).

Sim_Ling: This input variable represents the

lexical similarity. It has associated the following

linguistic terms: D

ling

= {Low(L), Regular(R),

Medium(M), High(H), Very High(VH)}. Because of

the distribution of lexical similarity values, equally

spaced fuzzy sets were defined. Membership

functions are shown in Figure 5(b).

Basic_Similarity: This variable defines the fuzzy

system layer output. It has associated the following

linguistic terms: D

Basic

= {Very Low(VL),

Figure 5: Fuzzy triangular-shaped membership functions

for: a) Sim_Jaccard, b) Sim_Ling and c) Basic_Similarity.

Low(L), Medium Low(ML), Regular(R), Medium

High(MH), High(H), Very High(VH)}. Membership

functions are shown in Figure 5(c).8

4.3 Structural Layer

The third layer of similarity fuzzy system is the

structural layer. This layer contains two fundamental

modules: The relational structure similarity module,

which uses the relational hierarchy of the ontologies;

and the internal structure similarity module.

4.3.1 Relational Structure Similarity

The relational structure module performs the

hierarchical similarity calculation. We defined four

input variables and one output. Each of them has

associated following linguistic terms: D

adv

= {Very

Low, Low, Medium Low, Regular, Medium High,

High, Very High}, whose semantics has been

represented by triangular membership functions as

in Figure 5(c). These variables are:

Sim_Basic: Represents the basic similarity value

calculated from the semantic and lexical similarities.

Extra_Siblings: Represents the “Extra” value of

the sibling’s similarity.

Extra_Parents: Represents the “Extra” value of

the parent’s similarity.

Extra_Descendants: Represents the “Extra”

value of the descendant’s similarity.

Sim_hierarchy: Represents the value of the

relational structure similarity.

The values of the “Extra” similarities provided

by the taxonomic hierarchy are calculated in the

relational structure module, in the manner explained

in Section 3.3. The rest of the input values have been

obtained from the previous layers.

4.3.2 Internal Structure Similarity

The internal structure similarity module performs

the property similarity calculation. This layer

receives the input values of the lexical similarity of

properties from previous layers, and the rest of the

input values are calculated on the internal structure

module as described in section 3.3. For the property

similarity we defined three input variables and one

output. These variables are:

Sim_ling: Represents the lexical similarity of the

property names. It has associated the following

linguistic terms set: D

ling

= {Low, Medium, High}.

Membership functions are shown in Figure 6(a).

Sim_domain: Represents the hierarchical

similarity of the classes to which they belong. It has

associated the following linguistic terms set: D

dom

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

102

{Very Low, Low, Medium Low, Regular, Medium

High, High, Very High}. Membership functions are

shown in Figure 6(b).

Sim_Range: Represents the similarity of the

range class if it is an object property, and the

similarity of the data type if it is a data property. It

has associated the following linguistic term sets:

range

= {Low, High}. Membership functions are

shown in Figure 6(c).

Sim_Prop: Represents the property similarity.

The fuzzy sets and the membership functions are the

same as in Sim_domain.

a) b)

Figure 6: Fuzzy triangular-shaped membership functions

for: a) Sim_ling, b) Sim_Domain and c) Sim_Range.

4.4 Align Layer

The align layer is for the improvement of the final

similarity. We defined three input variables and one

output. These variables are:

Sim_hierarchy: Represent the hierarchical

similarity of the two classes. It has associated the

following linguistic terms set: D

hier

= {Very Low,

Low, Medium Low, Regular, Medium High, High,

Very High}. Membership functions are the same in

Figure 6(b).

Extra_Prop: Represents the “Extra” value of

property similarity. It has associated the following

linguistic terms set: D

extra_prop

= {Low, Medium,

High}. Membership functions are the same in Figure

6(a).

Prop_number: It is a binary input variable that

represents if the two classes have the same number

of properties or not. It has associated the following

linguistic terms sets: D

PNumber

= {Low, High}.

Membership functions are the same in Figure 6(c).

Sim_final: This output variable represents the

value of the final similarity. The fuzzy sets and the

membership functions are the same as in

Sim_hierarchy.

Input values of this layer of the fuzzy system are

obtained from the structural layer. After calculating

the final similarity we proceed to formalize the

output alignments of the application. For this last

step we consider as valid those alignments whose

similarity is higher than 80%.

4.5 Evolutive Learning of the Fuzzy

Rule Bases

The rule bases of the fuzzy system were deduced

using the genetic algorithm Thrift (Thrift, 1991) for

the learning of rule bases. This method works by

using a complete decision table that represents a

special case of crisp relation defined over the

collections of fuzzy sets. A chromosome is obtained

from the decision table by going row-wise and

coding each output fuzzy set as an integer. The used

dataset has information of 40 ontologies mapped by

experts and it was partitioned with a 10-Fold Cross

Validation method. The input parameters of the

algorithm were the following: Population Size=61,

Number of Evaluations=1000, Crossover

Probability=0.6, Mutation Probability=0.1

The rule bases of the lexical and basic layers are

shown in Table 1 and Table 2 respectively. Due to

space reasons we do not show the rest of the rule

bases of the system.

Table 1: Rule Base of the lexical layer.

Synonym

Derivation

L R M H VH

L L R R M M

R R R R M H

M M M M H VH

H H H H VH VH

VH VH VH VH VH VH

Table 2: Rule Base of the basic layer.

Jacc

Ling

L R M H VH

L VL L ML R MH

R L ML R MH H

M L ML R MH H

H ML R MH H VH

VH ML MH H H VH

5 EVALUATION MEASURES

5.1 Precision

Precision is the fraction of correct instances among

FuzzyAlign-AFuzzyMethodforOntologyAlignment

103

those that the algorithm believes to belong to the

relevant subset (Rijsbergen, 1979). Given a

reference alignment R, the precision of some

alignment A is given by:

(,)

PAR







(4)

5.2 Recall

Recall (Rijsbergen, 1979) is computed as the

fraction of correct instances among all instances that

actually belong to the relevant subset. Given a

reference alignment R, the recall of some alignment

A is given by:

(,)

PAR







(5)

5.3 F-Measure

The F-measure is used in order to aggregate the

result of precision and recall (Rijsbergen, 1979).

Given a reference alignment R and a number α

between 0 and 1, the F-Measure of some alignment

A is given by:



(,) (,)

(,)

(1 ) ( , ) ( , )

PAR RAR

MAR

PAR RAR









 



(6)

The higher α, the more importance is given to

precision with regard to recall. Often, the value α =

0.5 is used. This is the harmonic mean of precision

and recall.

6 EXPERIMENTS

AND EVALUATION

We conducted several experiments with the

Ontology Alignment Evaluation Initiative (OAEI)

tests datasets. Below we show the results from the

tests and a comparison with other methods. Those

methods are: AgrMaker (Cruz et al., 2009), ASMOV

(Jean-Mary et al. 2009), CODI (Noessner et al.,

2010), Eff2Match (Watson Wey et al., 2010),

GeRMeSMB (Quix et al. 2010) and SOBOM (Xu et

al., 2010).

6.1 Benchmark Test

The domain of this first test (Euzenat et al., 2010) is

Bibliographic references. It is based on a subjective

view of what must be a bibliographic ontology. The

systematic benchmark test set is built around one

reference ontology and many variations of it. The

ontologies are described in OWL-DL and serialized

in the RDF/XML format. The reference ontology

contains 33 named classes, 24 object properties, 40

data properties, 56 named individuals and 20

anonymous individuals. The tests are organized in

three groups: Simple tests (1xx) such as comparing

the reference ontology with itself, with another

irrelevant ontology; Systematic tests (2xx) obtained

by discarding features from some reference

ontology. It aims at evaluating how an algorithm

behaves when a particular type of information is

lacking; four real- life ontologies of bibliographic

references (3xx) found on the web and left mostly

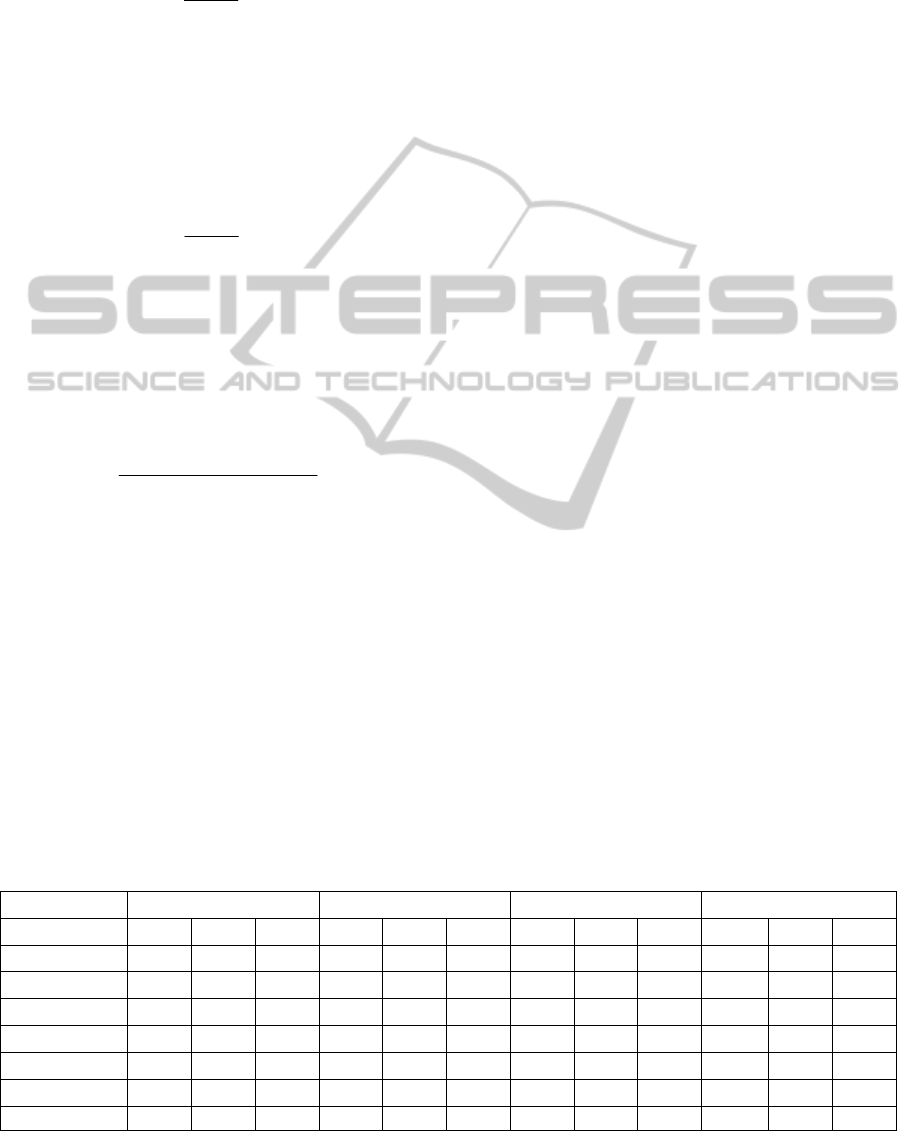
untouched. Table 3 shows the results of the

alignment methods that performed the benchmark

test by group of test.

It can be seen in the simple’s test (1xx) that the

performance of all the systems was optimal. For the

systematic tests (2xx) the FuzzyAlign system had a

high precision, surpassed only by ASMOV, however

we have obtained the best value of recall and f-

measure. For real cases (3xx) we have obtained the

same precision as AgrMaker and ASMOV, being

surpassed by Eff2Match and CODI, however we

have obtained the best recall and f-measure like

ASMOV. Finally looking at the harmonic means (H-

Mean) of precision, recall and f-measure of the three

phases, can be observed that our system achieved the

highest precision, recall and f-measure average

Table 3: Benchmark test results for the alignment methods in terms of precision, recall and F-measure.

Test 1xx 2xx 3xx H-Mean

System P R F P R F P R F P R F

AgrMaker 0.98 1.00 0.99 0.95 0.84 0.89 0.88 0.53 0.66 0.93 0.74 0.82

ASMOV 1.00 1.00 1.00 0.99 0.89 0.94 0.88 0.84 0.86 0.95 0.91 0.93

CODI 1.00 0.99 0.99 0.70 0.42 0.53 0.92 0.43 0.59 0.85 0.52 0.65

Eff2Match 1.00 1.00 1.00 0.98 0.63 0.77 0.89 0.71 0.79 0.95 0.75 0.84

GeRMeSMB 1.00 1.00 1.00 0.96 0.66 0.78 0.79 0.38 0.51 0.91 0.58 0.71

SOBOM 1.00 1.00 1.00 0.97 0.94 0.95 0.77 0.70 0.73 0.90 0.86 0.88

FuzzyAlign 1.00 1.00 1.00 0.98 0.95 0.97 0.88 0.84 0.86 0.95 0.93 0.94

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

104

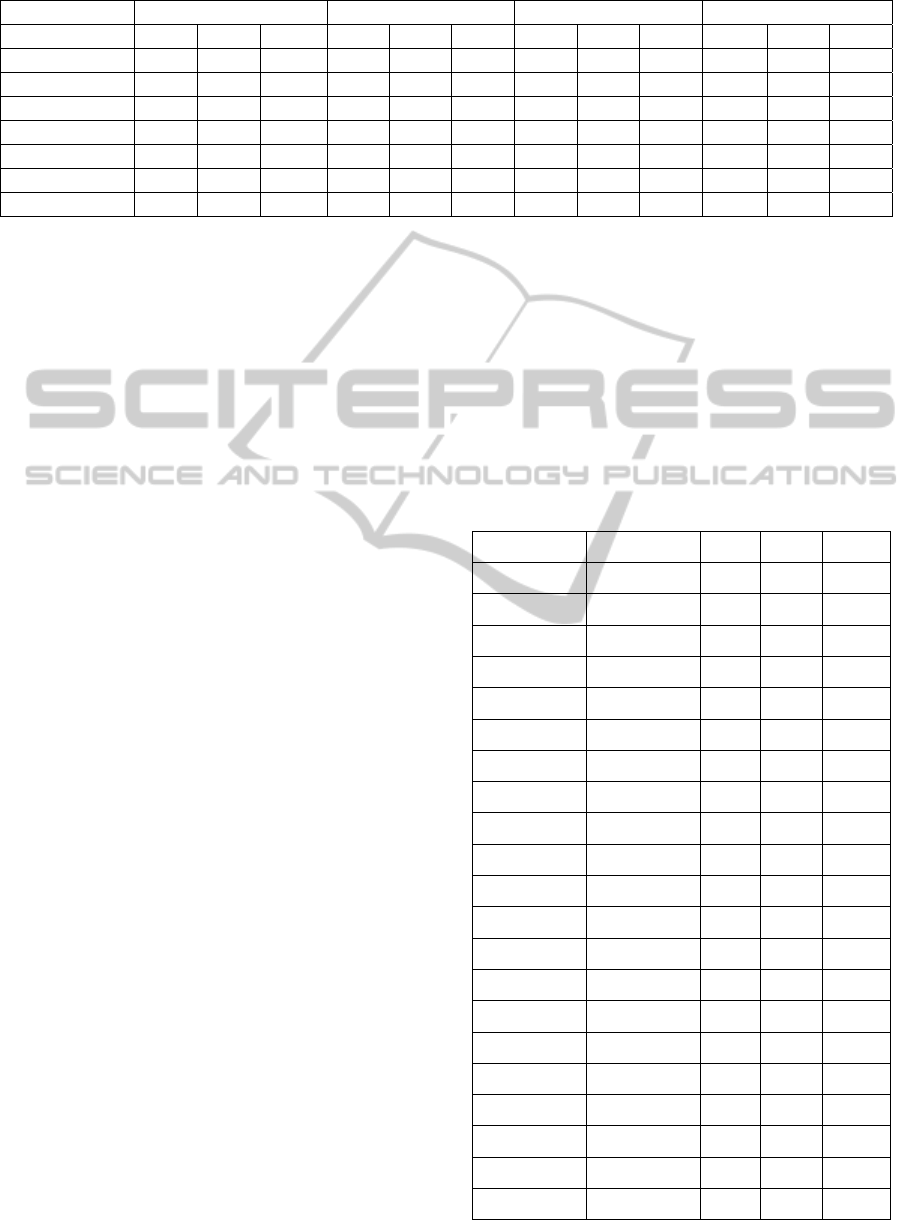
Table 4: Anatomy test results for the alignment methods in terms of precision, recall and F-measure.

Task #1 Task #2 Task #3 H-Mean

System P R F P R F P R F P R F

AgrMaker 0.90 0.85 0.87 0.96 0.75 0.84 0.77 0.87 0.82 0.87 0.82 0.84

ASMOV 0.79 0.77 0.78 0.86 0.75 0.81 0.71 0.79 0.75 0.78 0.77 0.79

CODI 0.96 0.65 0.77 0.96 0.66 0.78 0.78 0.69 0.73 0.89 0.66 0.76

Ef2Match 0.95 0.78 0.85 0.96 0.74 0.84 0.95 0.78 0.85 0.95 0.77 0.85

GeRMeSMB 0.88 0.31 0.46 0.88 0.31 0.46 0.08 0.89 0.15 0.20 0.39 0.27

SOBOM 0.95 0.78 0.86 - - - - - - - - -

FuzzyAlign 0.72 0.74 0.73 0.75 0.45 0.56 0.44 0.76 0.56 0.61 0.62 0.64

results, outperformed all the other systems. The

confidence threshold used for the selection of the

valid alignment was 0.8.

6.2 Anatomy Test

This track consists of two real world ontologies to be

matched (Euzenat et al., 2010). The source ontology

describes the Adult Mouse Anatomy (with 2744

classes) while the target ontology is the NCI

Thesaurus describing the Human Anatomy (with

3304 classes). The anatomy test consists of four

subtracks: subtrack 1, which emphasizes f-measure,

subtrack 2, which emphasizes precision, subtrack 3,

which emphasizes recall, and subtrack 4, which tests

the capability of extending a partial reference

alignment. We performed only the Tasks#1 through

#3 and use the following configuration parameters:

Task #1. The optimal solution alignment is

obtained by using the default parameter settings.

Confidence threshold value was 0.8.

Task#2. The alignment with optimal precision is

obtained by changing the threshold for valid

mappings to 0.9.

Task#3. The alignment with optimal recall is

generated by changing the threshold to 0.6.

The execution time for these tasks was

approximately 8 hours and 30 minutes. This is due

to there are too large ontologies. In Table 4 we can

observe the results of the 7 systems in the anatomy

test per track. In the case of SOBOM they have only

performed the Task#1.

The results of this test for FuzzyAlign were not

the best. This is mainly due to the fact that the

domain of ontologies are very specific and our

system is designed to map more general ontologies,

giving much weight to the lexicon. In this case the

use of WordNet instead of a medical board causes

that system not achieved optimal lexical similarities

and the lack of this information affected the overall

result.

6.3 Conference Test

Conference test (Euzenat et al., 2010) contains quite

real-case ontologies suitable because of their

heterogeneous character of origin. The goal of this

experiment is to find all correct correspondences

within a collection of ontologies describing the

domain of organizing conferences. In table 5 we

show the results of applying our system with 21

Table 5: Conference test results of FuzzyAlign in terms of

precision, recall and f-measure.

Ontology 1 Ontology 2 P R F

cmt Conference 0.85 0.85 0.85

cmt Confof 0.83 0.29 0.43

cmt Edas 0.88 0.88 0.88

cmt Ekaw 0.83 0.83 0.83

cmt Iasted 1.00 1.00 1.00

cmt Sigkdd 1.00 0.47 0.64

Conference Confof 1.00 1.00 1.00

Conference Edas 0.75 0.75 0.75

Conference Ekaw 0.80 0.70 0.85

Conference Iasted 0.97 1.00 0.99

Conference Sigkdd 1.00 1.00 1.00

Confof Edas 1.00 0.42 0.59

Confof Ekaw 1.00 0.35 0.52

Confof Iasted 1.00 1.00 1.00

Confof Sigkdd 0.66 1.00 0.80

Edas Ekaw 1.00 0.28 0.44

Edas Iasted 1.00 0.44 0.61

Edas Sigkdd 0.88 0.44 0.59

Ekaw Iasted 1.00 1.00 1.00

Ekaw Sigkdd 1.00 1.00 1.00

Iasted Sigkdd 1.00 0.86 0.92

FuzzyAlign-AFuzzyMethodforOntologyAlignment

105

reference alignments, corresponding to the complete

alignment space between 7 ontologies from the

conference data set. Table 6 shows the values of

precision, recall and f-measure obtained by the 7

systems that we compared, and the confidence

threshold set by each of them to provide the highest

average of f-measure. In the case of CODI they not

provided a confidence threshold because their results

were the same regardless of the threshold. We can

observe that with a confidence threshold of 0.8 our

system scored precision, recall and f-measure much

higher than others. This means that we are

considering as valid alignment only those mappings

whose similarity value is greater than 80%, which

shows that the system has shown better results with

a greater level of rigor in the selection of alignments.

Table 6: Conference test results for the alignment methods

in terms of confidence threshold, precision, recall and f-

measure.

System Threshold P R F

AgrMaker 0.66 0.53 0.62 0.58

ASMOV 0.22 0.57 0.63 0.60

CODI - 0.86 0.48 0.62

Ef2Match 0.84 0.61 0.58 0.60

GeRMeSMB 0.87 0.37 0.51 0.43

SOBOM 0.35 0.56 0.56 0.56

FuzzyAlign 0.80 0.93 0.74 0.83

7 CONCLUSIONS

AND FUTURE WORK

This article describes our work aimed at providing a

method to assist experts in the ontology alignment

process using fuzzy logic techniques. We propose

FuzzyAlign, a Multi-Layer Fuzzy System which

computes the similarities between entities from

different ontologies, taking into account semantic

and lexical elements and also the relational and the

internal structures of the ontologies. The system has

been tested in three of the basic tests proposed for

OAEI to evaluate the performance of ontology

alignment methods, showing better results than

others systems in general purpose ontologies and

ontologies from real life with correct lexical

constructions.

Through our experiments yield satisfactory

results, there are some limitations inherent to our

approach. Due to the importance of linguistic in the

process of matching and the use of WordNet, the

system not provides optimal results in very specific

domain ontologies. In addition the execution time of

the system increases when processing too large

ontologies due to the high amount of information.

Finally, as future work we intend to improve the

scalability of the application. We plan also to use

more linguistic tools, such as other lexical domain-

specific directories, like the Unified Medical

Language System (UMLS) metathesaurus for

medical ontologies, and thus ensure better results in

this types of ontologies. We also are interested in

extending the technique to propose an integration

model that allows matching taking into account the

use of other relations in real domains instead of just

equivalence.

ACKNOWLEDGEMENTS

This work is part of the RESULTA Project,

supported by the Spanish Ministry of Industry,

Tourism and Trade, TSI-020301-2009-31.

REFERENCES

Cordón, O., Herrera, F., Hoffman, F., Magdalena, L.

(2001): Genetic Fuzzy Systems. Evolutionary Tuning

and Learning of Fuzzy Knowledge Bases. World

Scientific, Singapore 2001.

Cruz, Isabel F., Palandri, Antonelli Flavio, and Stroe,

Cosmin. (September 2009): AgreementMaker

Efficient Matching for Large Real-World Schemas and

Ontologies. In International Conference on Very

Large Databases, Lyon, France, pages 1586-1589,

Doan A., Madhavan, J., Domingos, P., Halevy, A.,

(2004).: Ontology Matching: A Machine Learning

Approach. Handbook on Ontologies in Information

Systems. In: S. Staab and R. Studer (eds.), Invited

paper. Pp. 397-- 416. Springer-Velag

Euzenat, J., Ferrara, A., Hollink, L., Isaac, A., Joslyn, C.,

Malais´e, V., Meilicke, C., Nikolov, A., Pane, J.,

Sabou, M., Scharffe, F., Shvaiko, P., Spiliopoulos, V.,

Stuckenschmidt, H., ˇSv´ab-Zamazal, O., Sv´atek, V.,

dos Santos, C.T., Vouros, G., Wang, S. (2009) :

Results of the Ontology Alignment Evaluation

Initiative 2009. In: Proceedings of the 4th

International Workshop on Ontology Matching (OM-

2009). vol. 551. CEUR Workshop Proceedings,

http://ceur-ws.org

Euzenat, J, Shvaiko, P., Giunchiglia, F., Stuckenschmidt,

H., Mao, M., Cruz, I. (2010): Results of the Ontology

Alignment Evaluation Initiative 2010. In: Proceedings

of the 5th International Workshop on Ontology

Matching (OM-2010).

Fellbaum, C. (1998). WordNet: An Electronic Lexical

Database. MIT Press. 3.0, Cambridge, MA.

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

106

Fernández, S., Velasco, Juan R., Lopez-Carmona, Miguel

A. (2009). In: Proceedings of the 12 International

conference Priniciples of Practice in Multi-Agent

Systems (PRIMA 2009), Nagoya, Japan

Jean-Mary Y., Shironoshita E.P., Kabuka, M. (2009).

Ontology Matching with Semantic Verification.

Journal of Web Semantics. Sci. Serv. Agents World

Wide Web, doi: 10.1016/j.websem.2009.04.001

Noessner, J., Niepert, M., Meilicke, C. and

Stuckenschmidt, H. (2010). Leveraging

Terminological Structure for Object Reconciliation.

The Semantic Web: Research and Applications, p

334–348,.

Noy, N. F, Musen, M. A. (October 1999): SMART:

Automated Support for Ontology Merging and Align-

ment. In: 12th Workshop on Knowledge Acquisition,

Modelling and Management (KAW’99), Banff,

Canada.

Noy, N. F, Musen, M. A. (2003): The PROMPT suite:

Interactive tools for ontology merging and mapping.

International Journal of Human-Computer Studies,

59(6), pp. 983–1024

Noy, N. F, Musen, M. A. (August 2002): PROMPTDIFF:

A Fixed-Point Algorithm for Compar-ing Ontology

Versions. In: 18th National Conference on Artificial

Intelligence (AAAI’02), Edmonton, Alberta, Canada.

OAEI. www.oaei.ontologymatching.org

Osinski, Stanislaw, Jerzy Ste-fanowski, and Dawid Weiss.

(2004). "Lingo: Search Results Clustering Algorithm

Based on Singular Value Decom-position." In:

Proceedings of the International IIS: IIP-WMÂ´04

Conference, Zakopane, Poland. 359-68.

Pan, R., Ding, Z., Yu, Y., Peng, Y. (October 2005): A

Bayesian Network Approach to Ontology Mapping.

In: The Semantic Web –ISWC 2005, Vol. 3729/2005,

pp. 563—577. Springer Berlin/ Heidelberg

Porter, M.F. (1980) An Algorithm for Suffix Stripping,

Program, 14(3): 130–137.

Quix, C., Gal, A., Sagi, T., Kensche, D. (2010). An

integrated matching system: GeRoMeSuite and SMB–

Results for OAEI 2010. In: Proceedings of the 5th

International Workshop on Ontology Matching (OM-

2010)

Rijsbergen, V., C. J. (1979): Information Retrieval.

Butterworths. Second Edition, London

Thrift, P. (1991). Fuzzy Logic Synthesis with genetic

algorithms. In: Proceedings 4th International

Conference on Genetic Algorithms, Morgan

Kaufmann, 509-513.

UMLS. Unified Medical Language System.

http://umlsks.nlm.nih.gov/

Wang, S., Wang, G., Liu, X. (2010). Results of the

Ontology Alignment Evaluation Initiative 2010. In:

Proceedings of the 5th International Workshop on

Ontology Matching (OM-2010).

Watson Wey, K., Jun Jae, K. (2010). Eff2Match results for

OAEI 2010. In: Proceedings of the 5th International

Workshop on Ontology Matching (OM-2010).

Wikipedia. www.wikipedia.org

Xu, P., K., Wang, Y., Cheng, L., Zang, T. (2010).

Alignment Results of SOBOM for OAEI 2010. In:

Proceedings of the 5th International Workshop on

Ontology Matching (OM-2010).

FuzzyAlign-AFuzzyMethodforOntologyAlignment

107