Combining Qualitative Spatial Reasoning and Ontological Reasoning for

Supporting Robot Tasks

Lothar Hotz, Pascal Rost and Stephanie von Riegen

HITeC e.V. c/o Fachbereich Informatik, Universit

at Hamburg, Hamburg, Germany

Keywords:

Qualitative Spatial Reasoning, Ontological Reasoning, Cognitive Robotics, Knowledge-based Systems

Applications.

Abstract:

This paper presents an application of spatial and ontology reasoning technologies for mobile robot tasks. We

provide a combination of the spatial reasoning calculi RCC-8 and CDC as well as their integration with OWL-

based ontologies. An architecture that combines inference tools like Prolog, description logic reasoners, and

complex-event processing implements our approach. We illustrate the results with a mobile robot scenario

in a restaurant. In this paper, global path-ﬁnding demonstrates the use of qualitative spatial and ontological

reasoning.

1 INTRODUCTION

The research ﬁeld cognitive robotics addresses the use

of general logical representation and reasoning meth-

ods and tools for controlling robots in dynamic and in-

completely known worlds (Levesque and Lakemeyer,

2007). Following this direction, qualitative spatial

reasoning provides a mean for representing and rea-

soning about spatial occurrences like The plate is on

the table. or The robot is close to the guest. Espe-

cially the abstraction provided by qualitative repre-

sentations enables effective and short representations

about the quantitative world of robots. Such repre-

sentation support robot’s tasks like interaction ability

or path ﬁnding. Qualitative spatial reasoning enables

the explicit representation of spatial interrelations of

regions or objects. Its use for autonomous, mobile

robots is still a research topic. Especially, if all main

spatial dimensions (i.e. topology, orientation, and dis-

tance) shall be considered (Renz and Nebel, 2007).

Because typical spatial calculi focus on one dimen-

sion (e.g. Region Connection Calculus (RCC) (Ran-

dell et al., 1992) on topology and Cardinal Direction

Calculus (CDC) (Goyal, 2000) on orientation), the

combination of qualitative spatial calculi becomes im-

portant.

For representing robot’s knowledge about objects

and the environment, ontologies can be applied. By

using this approach, domain knowledge (like objects

and environments) and application knowledge (like

activities for serving a guest in a restaurant) can be

made explicit to the robot. Enhancing ontological

reasoning with qualitative spatial reasoning is a chal-

lenging task, because, if combining both, the ability to

reason about spatial knowledge and recognize incon-

sistencies gets lost, or the decidability of ontological

reasoning gets lost (Katz and Grau, 2005). Further-

more, the concrete contribution of qualitative and on-

tological reasoning for robot tasks is not ﬁnally clear.

Thus, in this paper, we present a case study about

combining two qualitative spatial calculi, i.e. RCC

and CDC, with ontological representations in a robot

scenario. We start with a concrete scenario dealing

with a robot acting in a restaurant environment and

extract requirements for the technologies (Section 2).

Then, we provide a short overview of applied rep-

resentation techniques, RCC, CDC, and ontological

reasoning (Section 3). Section 4 presents our inte-

grated approach which is evaluated by implementing

a system using Prolog, the complex event processing

ETALIS (Event Transaction Logic Inference System),

and the Web Ontology Language OWL (Antoniou and

Harmelen, 2003) (see Section 5). We conclude with a

summary in Section 6.

2 USE CASES AND

REQUIREMENTS

An interesting environment for illustrating the use

of knowledge representation techniques for service

377

von Riegen S., Hotz L. and Rost P..

Combining Qualitative Spatial Reasoning and Ontological Reasoning for Supporting Robot Tasks.

DOI: 10.5220/0004140003770380

In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2012), pages 377-380

ISBN: 978-989-8565-30-3

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

robot tasks is a restaurant environment. In such an

environment, domain-speciﬁc objects, concepts, and

rooms have to be represented. Objects might have hi-

erarchical relations and temporal or spatial relation-

ships to each other. Terminological knowledge about

dishes, drinks, meals etc. is needed. Areas which

may contain food products may be distinguished from

seating areas. For our experiments demonstrated in

this paper, we consider an artiﬁcial restaurant layout

as it is presented in Figure 1.

One requirement that have to be fulﬁlled for pro-

cessing such scenarios is that the robot shall identify

an ideal path to a table, i.e. using the spatial conﬁgu-

ration of the environment the robot shall infer, if a cer-

tain place is reachable and how the path to it is (global

path-ﬁnding, see Section 4). Another task would be to

compute if the current position of the robot is suitable

for placing a cup on the counter, i.e. to infer if the ac-

tual position is practical to interact with a target object

(interaction ability, see (Rost et al., 2012)).

3 BACKGROUND

The basic techniques we combine in our approach are

qualitative spatial reasoning and ontological reason-

ing.

Spatial calculi represent relations between objects

with ﬁnite sets of binary relations. They can de-

rive new knowledge and check if a provided knowl-

edge base is consistent. RCC enables reasoning

about topological properties of regions. Especially

RCC-8 provides eight spatial relations disconnected

(DC), externally connected (EC), tangential proper

part (TPP), non-tangential proper part (NTPP), par-

tially overlapping (PO), equal (EQ), and the inverses

T PP

and NT PP

The Cardinal Direction Calculus (CDC) enables

reasoning about relative orientation between objects

by using the eight cardinal points (N, NE, E, SE, S,

SW, W, NW) as well as one further relation for repre-

senting direct neighborhood (i.e. bounding box, B).

When using a calculus like RCC-8 or CDC the ba-

sic inference mechanism is based on a composition

operator ◦. Let D be a set of regions and R

, R

relations of the qualitative calculus: R

◦ R

{ (x R

z) | ∃y ∈ D : ((x R

y) ∧ (y R

z))}. Thus, a

composition operator computes the relation between

two regions x and z on the basis of a further region y

which is related to x and z. A composition table for a

certain calculus can be used to compute the composi-

tion operator (Goyal, 2000).

Through an ontological language like OWL it is

possible to represent knowledge about objects, activi-

ties, relations etc. of a domain. By providing a formal

representation such ontologies are exchangeable and,

more important, they can be used for inference ser-

vices (e.g. provided by Description Logic Reasoners,

(DL reasoner)). Means for representation are the sep-

aration of instances (representing individual objects)

from concepts (as set of instances), taxonomic rela-

tions between concepts, and properties as a further

type of relation between concepts. A TBox contains

all concepts and an ABox all instances.

However, the combination of OWL and qualitative

calculi is not straight forward. Especially to combine

both, RCC-8 and CDC (for topology and orientation)

with an ontology is not yet elaborated (at least to our

knowledge).

4 CONCEPTUAL APPROACH

For applying qualitative spatial reasoning in a mobile

robot environment as presented in Section 2, we de-

veloped the following approach.

For getting a representation of the domain knowl-

edge a TBox is used for representing classes occur-

ring in the environment (like cup, plate, table, room

etc.). ABox instances represent concrete individual

objects (like table1, counter1 etc.). Object properties

of OWL (Ob jectProperty) can be used for represent-

ing qualitative relations of the calculi. Object proper-

ties follow the same semantics as relations do.

For computing the consistency of the provided

facts and computing all spatial relationships of all ob-

jects in the environment, we use the introduced cal-

culi RCC-8 and CDC. Here, we apply a basic prop-

erty of OWL-ontologies, i.e. machine readability. By

automatically accessing ABox instances of the ontol-

ogy, we extract the instances and their relations from

the ABox and import them into a constraint system

which uses the composition table for the mentioned

inference tasks. The constraint system uses the path-

consistency algorithm for making implicit spatial re-

lations between domain objects (instances) explicit.

After doing so, new spatial relations can be imported

into the ABox. Thus, we combine the ontology (and

a DL reasoner) with a qualitative spatial constraint

system instead of including spatial calculi in a DL

reasoner directly. Our approach is similar to Pellet-

Spatial (Bhatt et al., 2009), however, with two spatial

calculi. In summary, using an ontology enables a cen-

tral point of interchangeable knowledge needed by a

robot for fulﬁlling its tasks, ensuring consistency of

the knowledge through its formal representation, and

making implicit knowledge (here about spatial occur-

rences) explicit by inference methods.

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

378

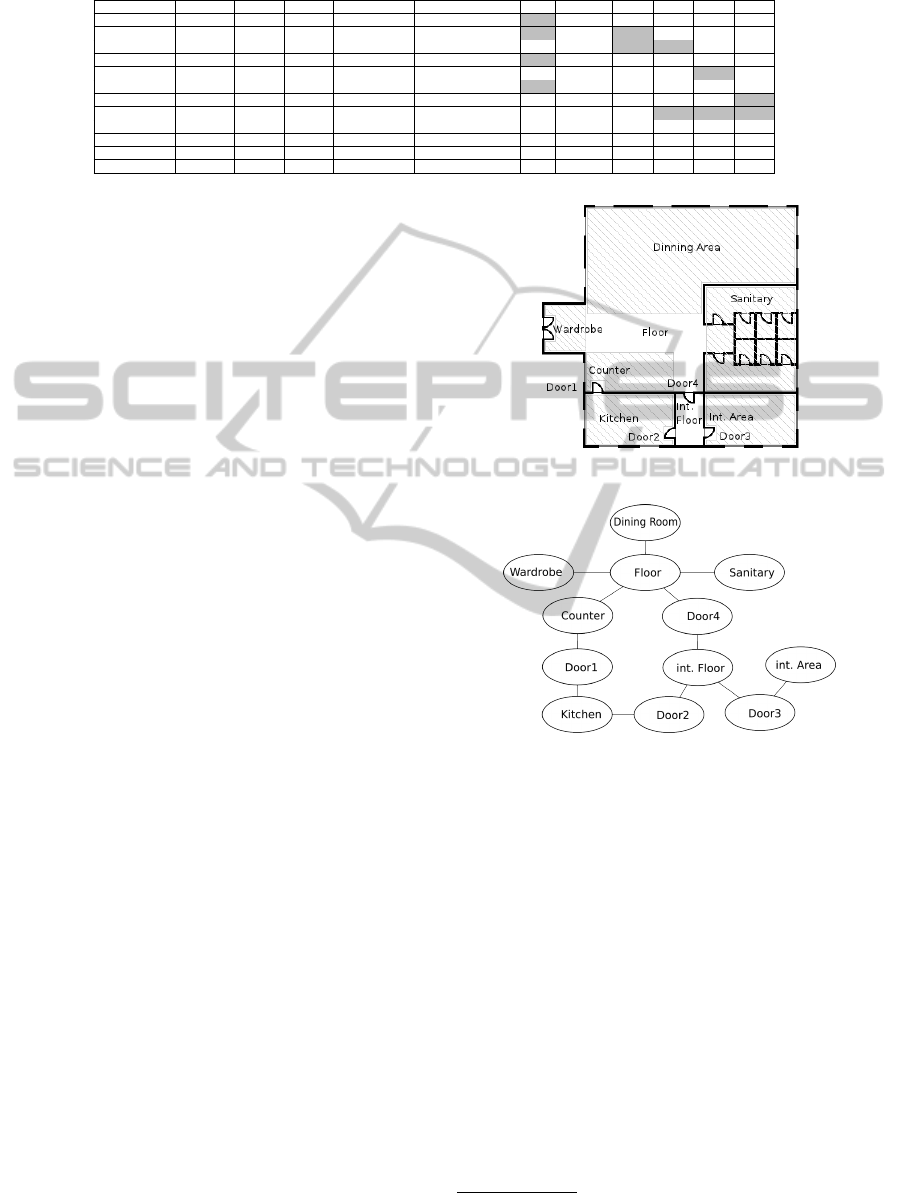
Table 1: Spatial conﬁguration of the rooms modeled with RCC-8.

Wardrobe Counter Kitchen Dining Room int. Area Sanitary Floor int. Floor Door1 Door2 Door3 Door4

Wardrobe EQ EC DC EC DC DC PO DC DC DC DC DC

Counter EQ EC DC DC DC PO DC PO DC DC DC

Kitchen EQ DC DC DC DC EC PO PO DC DC

Dining Room EQ DC EC PO DC DC DC DC DC

int. Area EQ EC DC EC DC DC PO DC

Sanitary EQ PO DC DC DC DC DC

Floor EQ EC DC DC DC PO

int. Floor EQ DC PO PO PO

Door1 EQ DC DC DC

Door2 EQ DC DC

Door3 EQ DC

Door4 EQ

Qualitative spatial reasoning with RCC and CDC

can be used for computing a path from a start to

an end point. In the following, we consider global

path-ﬁnding from a point A to B without taking ob-

stacles into account. Handling obstacles would in-

volve local path-ﬁnding algorithms. Typically applied

global path-ﬁnding algorithms represent the search

environment as an undirected, weighted graph (Dijk-

stra, 1959). For making use of this source, our ap-

proach maps qualitative representations of the envi-

ronment from the ontology into undirected graphs and

applies one of these algorithms. If the ontology is not

(manually) populated with pre-existing spatial conﬁg-

urations of the rooms in the environment, the popula-

tion process could be done with a combined SLAM

(Simultaneous Localization and Mapping) and image

processing approach. The exact procedure of auto-

matic population of spatial conﬁgurations is an ongo-

ing research topic.

Following scenario illustrates the mapping of a

spatial conﬁguration into a graph for computing a

global path. A robot needs to compute a global path

for getting from the kitchen to the dining area. From

such a scenario, we model the undirected graph by

introducing for each room a node and the relations

between rooms as edges between nodes. As edges

we use RCC-8 relations, especially the relation PO

(overlapping) is used when there exists a direct path

from a room to another room. Thus, between two

nodes in the graph there exist exactly one edge, if

between the corresponding rooms or regions a PO

relation exists. The weight of the edge models the

quantitative distance between the rooms or is equal

1, if not known. Unknown, or uncertain spatial rela-

tions between different rooms can be computed with

the previously shown reasoning techniques. Figure

1 presents a sketch of the restaurant with rooms and

doors. The ﬂoor is separated into Floor and inter-

nal Floor (int. Floor). Table 1 represents the spatial

conﬁguration modeled with RCC-8 relations. Rela-

tions of type PO are bold, the rooms can be directly

reached. Each door is represented by an own region.

Figure 2 presents the undirected graph for this con-

ﬁguration. Edges have no weights, for simplicity rea-

Figure 1: Environment of the restaurant with doors.

Figure 2: Undirected, unweighted graph for global path-

ﬁnding.

sons. Such a graph can be used as input for typical

path-ﬁnding algorithms.

5 EVALUATION OF THE

APPROACH

For evaluating our conceptual approach, we imple-

mented an architecture that combines the needed in-

ference technologies. First, we represent the system

setup and then discuss some insights we had.

As a basic system, we use ETALIS

. This sys-

tem combines complex event processing (CEP) with

Prolog. Event processing enables the processing of

continuous data streams created through the sensors

of a robot. Prolog enables the representation and

http://code.google.com/p/etalis/

CombiningQualitativeSpatialReasoningandOntologicalReasoningforSupportingRobotTasks

379

dynamic adaptation of facts of the environment of

the robot, an external database is thus not necessary.

Compared to other CEP-systems, which are imple-

mented with procedural or object-oriented languages,

ETALIS is more ﬂexible and partially with good per-

formance. Our approach combines ETALIS with the

PROLOG-OWL interface THEA2 (Vangelis Vassil-

iadis, Chris Mungall, 2012), and DL reasoners to our

system called ETALIS-Spatial.

For knowledge representation, we create an OWL

knowledge base. Objects and spatial relations are de-

ﬁned as described in Section 3. THEA2 enables the

access to the ABox for extracting spatial relations and

all instances for participating objects. Furthermore,

THEA2 allows direct access to commonly used DL

reasoners, like Pellet

. ETALIS-Spatial starts with the

composition tables and applies a path-consistency al-

gorithm typically used for solving constraint satisfac-

tion problems (Tsang, 1993).

In summary, the evaluation shows an implemen-

tation of our conceptual approach presented in Sec-

tion 4. We applied RCC-8 and CDC to cover topol-

ogy and orientation aspects of spatial reasoning. The

qualitative spatial relations can be represented in an

OWL ontology as properties. The OWL-based ontol-

ogy acts furthermore as a central place for all needed

knowledge. The knowledge can be extracted from the

ontology for processing in a separate spatial Prolog-

based reasoner. Computing new spatial relations and

consistency checks are performed by a Prolog sys-

tem based on composition tables provided by the cal-

culi in combination with path-consistency algorithms.

Thereby, we use the implicit inherent information

about paths contained in RCC-8 relations for building

an undirected unweighted graph that again is used by

typical global path-ﬁnding algorithms. By using com-

plex event processing, a continuous stream of data

could be processed.

Our implementation uses the CEP-framework

ETALIS and enhances it to ETALIS-Spatial. We im-

plemented an ontology representing parts of a restau-

rant. In principle, such an ontology can be enhanced

to cover more facets of the tasks or other domain ar-

eas. Further or other qualitative calculi which han-

dle other aspects can be integrated into the system

by modeling their composition tables and relations in

Prolog.

6 CONCLUSIONS

This paper demonstrates the application of the quali-

http://clarkparsia.com/pellet/spatial/

tative spatial calculi RCC-8 and CDC for robot tasks.

The approach combines these calculi with ontological

reasoning by modeling the relations in OWL but com-

puting spatial inferences with logical programming.

Thus, consistency checking and computation of new

spatial relations could be performed. An extension

of the complex event processing framework ETALIS

implements our approach. We demonstrate it’s use in

a restaurant scenario and could show how qualitative

spatial reasoning can support tasks of mobile robots.

ACKNOWLEDGEMENTS

This work is supported by the RACE project, grant

agreement no. 287752, funded by the EC Seventh

Framework Program theme FP7-ICT-2011-7.

REFERENCES

Antoniou, G. and Harmelen, F. V. (2003). Web Ontology

Language: OWL. In Handbook on Ontologies in In-

formation Systems, pages 67–92. Springer.

Bhatt, M., Dylla, F., and Hois, J. (2009). Spatio-

terminological inference for the design of ambient en-

vironments. In COSIT, pages 371–391.

Dijkstra, E. W. (1959). A note on two problems in connex-

ion with graphs. Numerische Mathematik, 1:269–271.

Goyal, R. K. (2000). Similarity assessment for cardinal di-

rections between extended spatial objects. PhD thesis,

The University of Maine. AAI9972143.

Katz, Y. and Grau, B. C. (2005). Representing qualitative

spatial information in owl-dl. In Proceedings of the

OWL: Experiences and Directions Workshop. Galway.

Levesque, H. and Lakemeyer, G. (2007). Cognitive

Robotics. In van Harmelen, F., Lifschitz, V., and

Porter, B., editors, Handbook of Knowledge Represen-

tation. Elsevier.

Randell, D. A., Cui, Z., and Cohn, A. G. (1992). A spatial

logic based on regions and connection. In Proceedings

3rd International Conference On Knowledge Repre-

sentation and Reasoning.

Renz, J. and Nebel, B. (2007). Qualitative spatial rea-

soning using constraint calculi. In Aiello, M., Pratt-

Hartmann, I., and van Benthem, J., editors, Handbook

of Spatial Logics, pages 161–215. Springer.

Rost, P., Hotz, L., and von Riegen, S. (2012). Support-

ing Mobile Robot‘s Tasks through Qualitative Spatial

Reasoning. In Bernard, A. e. a., editor, 9th Interna-

tional Conference on Informatics in Control, Automa-

tion and Robotics. upcoming.

Tsang, E. (1993). Foundations of Constraint Satisfaction.

Academic Press, London, San Diego, New York.

Vangelis Vassiliadis, Chris Mungall (2012). A toolbox for

Qualitative Spatial Reasoning in applications. http://

www.semanticweb.gr/thea/index.html. Date: March,

10th 2012.

KEOD2012-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

380