
Probabilistic Sequence Modeling for Recommender Systems
Nicola Barbieri
1,2
, Antonio Bevacqua
1
, Marco Carnuccio
1
, Giuseppe Manco
2
and Ettore Ritacco
2
1
Department of Electronics, Informatics and Systems, University of Calabria, via Bucci 41c, 87036 Rende (CS), Italy
2
Institute for High Performance Computing and Networks (ICAR), Italian National Research Council,
via Bucci 41c, 87036 Rende (CS), Italy
Keywords:
Recommender Systems, Collaborative Filtering, Probabilistic Topic Models, Performance.
Abstract:
Probabilistic topic models are widely used in different contexts to uncover the hidden structure in large text
corpora. One of the main features of these models is that generative process follows a bag-of-words assump-
tion, i.e each token is independent from the previous one. We extend the popular Latent Dirichlet Allocation
model by exploiting a conditional Markovian assumptions, where the token generation depends on the cur-
rent topic and on the previous token. The resulting model is capable of accommodating temporal correlations
among tokens, which better model user behavior. This is particularly significant in a collaborative filtering
context, where the choice of a user can be exploited for recommendation purposes, and hence a more re-
alistic and accurate modeling enables better recommendations. For the mentioned model we present a fast
Gibbs Sampling procedure for the parameters estimation. A thorough experimental evaluation over real-word
data shows the performance advantages, in terms of recall and precision, of the proposed sequence-modeling
approach.
1 INTRODUCTION
Probabilistic topic models, such as the popular Latent
Dirichlet Allocation (LDA) (Blei et al., 2003), assume
that each collection of documents exhibits an hidden
thematic structure. The intuition is that each docu-
ment may exhibit multiple topics, where each topic is
characterized by a probability distribution over words
of a fixed size dictionary. This representation of the
data into the latent-topic space has several advan-
tages, as topic modeling techniques have been applied
to different contexts. Example scenarios range from
traditional problems (such as dimensionality reduc-
tion and classification) to novel areas (such as the gen-
eration of personalized recommendations). In most
cases, LDA-based approaches have been shown to
outperform state-of-art approaches.
Traditional LDA-based approaches propose a data
generation process that is based on a “bag-of-words”
assumption, i.e. such that the order of the items in a
document can be neglected. This assumption fits tex-
tual data, where probabilistic topic models are able
to detect recurrent co-occurrence patterns, which are
used to define the topic space. However, there are sev-
eral real-word applications where data can be “nat-
urally” interpreted as sequences, such as biological
data, web navigation logs, customer purchase his-
tory, etc. Interpreting sequence in accordance to “ex-
changeability”, i.e., by ignoring the intrinsic sequen-
tiality of the data within, may result in poor model-
ing: according to the bag-of-word assumption, co-
occurrences is modeled independently for each word,
via a probability distribution over the dictionary in
which some words exhibit an higher likelihood to ap-
pear than others. On the other hand, sequential data
may express causality and dependency, and different
topics can be used to characterize different depen-
dency likelihoods. In practice, a sequence expresses
a context which provides valuable information for a
more refined modeling.
The above observation is particularly noteworthy
when data expresses preferences made by users, and
the ultimate objective is to model a user’s behav-
ior in order to provide accurate recommendations.
The analysis of the sequential patterns has impor-
tant applications in modern recommender systems,
which are always more focused on an accurate bal-
ance between personalization and contextualization
techniques. For example, in Internet based stream-
ing services for music or video (such as Last.fm
1
and
Videolectures.net
2
), the context of the user interaction
1
http://last.fm
2
http://videolectures.net
75
Barbieri N., Bevacqua A., Carnuccio M., Manco G. and Ritacco E..
Probabilistic Sequence Modeling for Recommender Systems.
DOI: 10.5220/0004140700750084
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2012), pages 75-84
ISBN: 978-989-8565-29-7
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

with the system can be easily interpreted by analyz-
ing the content previously requested. The assumption
here is that the current item (and/or its genre) influ-
ences the next choice of the user.
Recommender systems have greatly benefited
from probabilistic modeling techniques based on
LDA. Recent works in fact have empirically shown
that probabilistic latent topics models represent the
state-of-the art in the generation of accurate person-
alized recommendations (Barbieri and Manco, 2011;
Barbieri et al., 2011b; Barbieri et al., 2011a). Prob-
abilistic techniques offer some advantages over tra-
ditional deterministic models: notably, they do not
minimize a particular error metric but are designed to
maximize the likelihood of the model given the data
which is a more general approach; moreover, they
can be used to model a distribution over rating values
which can be used to determine the confidence of the
model in providing a recommendation; finally, they
allow the possibility to include prior knowledge into
the generative process, thus allowing a more effective
modeling of the underlying data distribution. Notably,
when preferences are implicitly modeled through se-
lection (that is, when no rating information is avail-
able), the simple LDA best models the probability that
an item is actually selected by a user (Barbieri and
Manco, 2011).
A simple approach to model sequential data
within a probabilistic framework has been proposed
in (Cadez et al., 2000). In this work, authors present
a framework based on mixtures of Markov models
for clustering and modeling of web site navigation
logs, which is applied for clustering and visualiz-
ing user behavior on a web site. Albeit simple, the
proposed model suffers of the limitation that a sin-
gle latent topic underlies all the observation in a sin-
gle sequence. This approach has been overtaken by
other methods based on latent semantic indexing and
LDA. In (Wallach, 2006; X. Wang and Wei, 2007),
for example, the authors propose extension of the
LDA model which assume a first-order Markov chain
for the word generation process. In the resulting Bi-
gram Model (BM) and Topical n-grams, the current
word depends on the current topic and the previous
word observed in the sequence. The LDA Collocation
Model (Griffiths et al., 2007) introduces a new set of
random variables (for bigram status) x which denotes
whether a bigram can be formed with the previous
word token. The bigram status adds a more realistic
than Wallach model which always generates bigrams.
Hidden Markov models (Bishop, 2006, Chapter
13) are a general reference framework for modeling
sequence data. HMMs assume that sequential data are
generated using a Markov chain of latent variables,
with each observation conditioned on the state of the
corresponding latent variable. The resulting likeli-
hood can be interpreted as an extension of a mixture
model in which the choice of mixture components for
each observation is not selected independently but de-
pends on the choice of components for the previous
observation. (Gruber et al., 2007) delve in this di-
rection, and propose an Hidden Topic Markov Model
(HTMM) for text documents. HTTM define a Markov
chain over latent topics of the document. The corre-
sponding generative process assume that all words in
the same sentence share the same topic, while succes-
sive sentences can either rely on the previous topic, or
introduce a new one. The topics in a document form
a Markov chain with a transition probability that de-
pends on a binary topic transition variable ψ. When
ψ = 1, a new topic is drawn for the n-th sentence, oth-
erwise the same previous topic is used.
Following the research direction outlined above,
in this paper we study the effects of “contextual”
information in probabilistic modeling of preference
data. We focus on the case where the context can be
inferred from the analysis of the sequence data, and
we propose a topic model which explicitly makes use
of dependency information for providing recommen-
dations. As a matter of fact, the issue has been dealt
with in similar papers (like, e.g. (Wallach, 2006)).
Here, we resume and extend the approaches in the lit-
erature. by concentrating on the effects of such mod-
eling on recommendation accuracy, as it explicitly re-
flects accurate modeling of user behavior.
In short, the contributions of the paper can be sum-
marized as follows.
1. We propose an unified probabilistic framework to
model dependency in preference data, and instan-
tiate the framework in accordance to a specific as-
sumption on the sequentiality of the underlying
generative process;
2. For the proposed instance, we provide the rela-
tive ranking function that can be used to generate
personalized and context-aware recommendation
lists;
3. We finally show that the proposed sequential mod-
eling of preference data better models the under-
lying data, as it allows more accurate recommen-
dations in terms of precision and recall.
The paper is structured as follows. In Sec. 2 we in-
troduce sequential modeling, and specify in Sec. 2.1
the corresponding item ranking functions for sup-
porting recommendations. The experimental evalu-
ation of the proposed approaches in then presented in
Sec. 3, in which we measure the performance of the
approaches in a recommendation scenario. Section 4
KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
76

Table 1: Summary of the notation used.
notation description
M # Users
N # Items
K # Topics
W Collection of users’ traces, W = {~w
1
,...,~w
M
}
n
u
# Items in the user u’s trace
~w
u
Item trace of user u, ~w
u
= {w
u,1
.w
u,2
.··· .w
u,N
u
−1
.w
u,n
u
}
w
u,n
n-th item in the trace of user u
Z Collection of topic traces for each user, Z = {~z
1
,...,~z
M
}
~z
u
Topic trace for user u,~z
u
= {z
u,1
.z
u,2
.··· .z
u,N
u
−1
.z
u,n
u
}
z
u,n
n-th topic in the trace of user u
n
k
d,i
number of times item i has been associated with
topic k for user d
n
k
(·),i. j
number of times item sequence i. j has been associated with
topic k in W
n
k
d,(·)
number of times an item has been associated with
topic k for user d
~
Θ matrix of parameters
~
θ
u
~
θ
u
mixing proportion of topics for the user u
ϑ
u,k
mixing coefficient of the topic k for the user u
~
Φ matrix of parameters
~
ϕ
k
= {ϕ
k, j.i
}
ϕ
k, j.i
mixing coefficient of the topic k for the item sequence j, i
concludes the paper with a summary of the findings
and mention to further extensions.
2 MODELING SEQUENCE DATA
Let U = {u
1
,. . ., u
M
} be a set of M users and I =
{i
1
,. . ., i
N
} a set of N items. In the general settings,
we consider a set W = {~w
1
,. . .,~w
M
} of user traces,
where ~w
u
= {w
u,1
,w
u,2
,·· · ,w
u,n
i
−1
.w
u,n
i
} is the trace
of all items selected by user u in sequence. We also
assume that each user action is characterized by a
latent factor triggering that action. That is, a latent
set Z = {~z
1
,. . .,~z
M
} is associated to the data, where,
again~z
u
= {z
u,1
,z
u,2
,·· · ,z
u,n
i
−1
.z
u,n
i
} is a latent topic
sequence, and z
d,n
∈ {1, .. . , K} is the latent topic as-
sociated with the item w
d,n
∈ I . By assuming that
~
Φ and
~
Θ are the distribution functions for W and Z
(with respective priors
~
β and
~
α, we can express the
complete likelihood as:
P(W,Z,
~
Θ,
~
Φ|
~
α,
~
β) =P(W|Z,
~
Φ)P(
~
Φ|
~
β)
· P(Z|
~
Θ)P(
~
Θ|
~
α)
(1)
where
P(W|Z,
~
Φ) =
M
∏
d=1
P(~w
d
|~z
d
,
~
Φ)
P(Z|
~
Θ) =
M
∏
d=1
P(~z
d
|
~
θ
d
)
and P(
~
Φ|
~
β) and P(
~
Θ|
~
α) are specified according to the
modeling. For example, in the standard LDA settings
where all terms are independent and exchangeable,
we have:
P(~w
d
|~z
d
,
~
Φ) =
n
d
∏
i=1
P(w
d,n
|z
d,n
,
~
Φ)
P(w|k,
~
Φ) =
N
∏
i=1
ϕ
δ
i,w
k,i
P(~z
d
|
~
θ
d
) =
n
d
∏
i=1
P(z
d,n
|
~
θ
d
)
P(z|
~
θ
d
) =
K
∏
k=1
ϑ
δ
k,z
d,k
P(
~
Θ|
~
α) =
M
∏
d=1
P(
~
θ
d
|
~
α)
P(
~
θ
d
|
~
α) =
Γ(
∑
K
k=1
α
k
)
∏
K
k=1
Γ(α
k
)
K
∏
k=1
ϑ
α
k
−1
d,k
P(
~
Φ|
~
β) =
K
∏
k=1
P(
~
ϕ
k
|
~
β
k
)
P(
~
ϕ
k
|
~
β
k
) =
Γ(
∑
N
i=1
β
k,i
)
∏
N
i=1
Γ(β
k,i
)
N
∏
i=1
ϕ
β
k,i
−1
k,i
Here, δ
h,k
represents the Kronecker delta. Figure
1(a) graphically describes the generative process. As
usual, the joint topic-data probability can be obtained
by marginalizing over the
~
Φ and
~
Θ components:
P(W,Z|
~
α,
~
β) =
Z
~
Φ
Z
~
Θ
P(W|Z,
~
Φ)P(
~
Φ|
~
β)P(Z|
~
Θ)
·P(
~
Θ|
~
α)d
~
Θd
~
Φ
In the following, we model further assumptions
on both w
d
and z
d
, which explicitly deny the ex-
changeability assumption. Several other models can
be obtained, which rely on more complex assump-
tions. However, the models delved in here subsume
the main characteristics of sequential modeling. We
observed that, in the real world, past decisions affect
future decisions. In particular we focused on the be-
havior of a user base which is used to frequently buy
items from a provider. A user tend to choose items ac-
cording her tastes, but her tastes change over the time
influenced by the purchased items. The sequence of
these items depends on the fact that nearly purchased
items are similar or share some features. For instance,
let us consider the sequence of items u.v.t: initially
the user bought the item u, then she chose v because
of its similarity to u and finally she acquired t, that
shares some features with v. Note that t should be
completely different from u, but because of the taste
change of the user they are in the same sequence. Ac-
cording to these assumptions, we choose to model the
item sequence as a stationary Markov Chain of order
1:
ProbabilisticSequenceModelingforRecommenderSystems
77

α
θ
z
1
w
2
w
1
w
Nd
z
2
z
Nd
Φ
β
M
(a) Latent Dirichlet Allocation
α
θ
z
1
w
2
w
1
w
Nd
z
2
z
Nd
Φ
β
M
. . .
(b) Token-Bigram Model
Figure 1: Graphical Models.
• we choose to use a Markov Chain because of the
sequential nature of the purchased item list, more-
over the Markov Chain can model the user’s taste
changing over the time;
• the chain is stationary because users frequently
buy items;
• the order of the chain is 1 because the probabil-
ity that two subsequent purchases share some fea-
tures or are dependent each other is higher than
that of two purchases distant in time.
All these aspects lead us to the definition of the Token-
Bigram Model, described as follows. We assume
that ~w
d
represents a first-order Markov chain, where,
each item selection w
d,n
depends on the recent history
w
d,n−1
of selections performed by the user. This is es-
sentially the same model proposed in (Wallach, 2006;
Cadez et al., 2000), and the probability of a user trace
can be expressed as
P(~w
d
|~z
d
,
~
Φ) =
N
d
∏
n=1
P(w
d,n
|w
d,n−1
,z
d,n
,
~
Φ) (2)
In practice, an item w
d,n
is generated according to
a multinomial distribution
~
φ
z
d,n
,w
d,n−1
which depends
on both the current topic z
d,n
and the previous items
w
d,n−1
. (Notice that when n = 1, the previous item
is empty and the multinomial resolves to
~
φ
z
d,n
, rep-
resenting the initial status of a Markov chain). As a
consequence, the conjugate prior has to be redefined
as:
P(
~
Φ|
~
β) =
K
∏
k=1
N
∏
m=0
P(
~
ϕ
k,m
|
~
β
k,m
)
=
K
∏
k=1
N
∏
m=0
Γ(
∑
N
n=1
β
k,m.i
)
∏
N
n=1
Γ(β
k,m.n
)
N
∏
n=1
ϕ
β
k,m.n
−1
k,m,n
Since the Markovian process does not affect the topic
sampling, both P(~z
d
|
~
θ
d
) and P(
~
Θ|
~
α) are defined as
in equation 2. The generative model, depicted in
Fig. 1(b), can be described as follows:
• For each user d ∈ {1,. . ., M} sample
user community-mixture components
~
θ
d
∼ Dirichlet(
~
α) and sequence length
n
d
∼ Poisson(ξ)
• For each user attitude k ∈ 1, . . . ,K and item v ∈
{0,. . ., N}
– Sample item selection components
~
ϕ
k,v
∼
Dirichlet(
~
β
k,v.
)
• For each user d ∈ {1, . . ., M} and n ∈ {1, .. . , n
d
}
– sample a user attitude z
d,n
∼ Discrete(ϑ
u
)
– sample an item i
d,n
∼ Discrete(
~
ϕ
z
d,n
,i
d,n−1
)
Notice that we explicitly assume the existence
of a family {
~
β
k,m
}
k=1,...,K;m=0,...,N
of Dirichlet coef-
ficients. As shown in (Wallach, 2006), different mod-
eling strategies (e.g., shared priors β
(k,m),n
= β
n
) can
affect the accuracy of the model.
KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
78

By algebraic manipulations, we obtain the follow-
ing joint item-topic distribution:
P(W,Z|α, β) =
M
∏
d=1
∆
~n
d,(·)
+
~
α
∆(
~
α)
!
·
K
∏
k=1
N
∏
m=0
∆
~n
k
(·),m.
+
~
β
k,m.
∆(
~
β
k,m.
)
(3)
The latter allows us to define a collapsed Gibbs sam-
pling procedure:
E Step: iteratively sampling of topics, according to
the probability
P(z
d,n
= k|
~
Z
−(d,n)
,
~
W ) ∝
n
k
d,(·)
+ α
k
− 1
·
n
k
(·),u.v
+ β
k,u.v
− 1
∑
N
r=1
n
k
(·),u.r
+ β
k,u.r
− 1
(4)
relative to the topic to associate with the n-th item
of the d-th document, exhibiting w
d,n−1
= u and
w
d,n
= v.
M Step: estimating both
~
Φ and
~
Θ, according to the
following equations:
ϑ
d,k
=
n
k
d,(·)
+ α
k
∑
K
k
0
=1
n
k
0
d,(·)
+ α
k
0
ϕ
k,r.s
=
n
k
(·),r.s
+ β
(k,r.s
∑
s
0
∈U
n
k
(·),r.s
0
+ β
(k,r).s
0
(5)
Log-likelihood. The data likelihood, given the
model parameters,
~
Θ,
~
Φ, is defined as follows:
P(W|
~
Θ,
~
Φ) =
M
∏
d=1
P(~w
d
|
~
θ
d
,
~
Φ) (6)
Where:
P(~w
d
|
~
θ
d
,
~
Φ) = P(w
d,n
d
,. . ., w
d,1
|
~
θ
d
,
~
Φ)
=
K
∑
k=1
P(w
d,n
d
,. . ., w
d,1
|z
d,n
d
= k,
~
θ
d
,
~
Φ)
· P(z
d,n
d
= k|
~
θ
d
)
=
K
∑
k=1
P(w
d,n
d
|z
d,n
d
= k, w
d,n
d
,
~
Φ)
· P(w
d,n
d
−1
,. . ., w
d,1
|
~
θ
d
,
~
Φ)
· P(z
d,n
d
= k|
~
θ
d
)
= P(w
d,n
d
−1
,. . ., w
d,1
|
~
Θ,
~
Φ)
·
K
∑
k=1
ϕ
k,w
d,n
d
,w
d,n
d
−1
· ϑ
d,k
(7)
This formulation triggers a recursive procedure for the
likelihood computation, whose trivial case is:
P(w
d,1
|
~
Θ,
~
Φ) =
K
∑
k=1
P(w
d,1
|,z
d,1
= k,
~
Φ)P(z
d,1
= k|
~
θ
d
)
=
K
∑
k=1
φ
k,w
d,1
,
· ϑ
d,k
(8)
Where
~
φ
k
represents the initial state probabilities, as
introduced above.
2.1 Item Ranking
The probabilistic framework is quite flexible, as it
provides in general different choices for item ranking
(Barbieri and Manco, 2011) an item for recommenda-
tion purposes. We next propose the functions relative
to each model to be tested in the experimental sec-
tion. In the following, we assume that a user can be
denoted by a unique index u, and a previous history is
given by ~w
u
of size n− 1. We are interested in provid-
ing a ranking for the n-th choice w
u,n
.
LDA. Following (Barbieri and Manco, 2011) we
adopt the following ranking function:
rank(i, u) = P(w
u,n
= i|~w
u
)
=
K
∑
k=1
P(i|z
u,n
= k)P(z
u,n
= k|
~
θ
u
)
=
K
∑
k=1
ϕ
k,i
· ϑ
u,k
(9)
It has been shows that LDA, equipped with the
above ranking function, significantly outperforms
the most significant approaches to modeling user
preferences. Hence, it is a natural baseline func-
tion upon which to measure the performance of
the other approaches proposed in this paper.
Token-bigram Model. The dependency of the cur-
rent selection from the previous history can be
made explicit, thus yielding the following upgrade
to the LDA ranking function:
rank(i, u) = P(w
u,n
= i|~w
u
)
=
K
∑
k=1
P(i|z
u,n
= k,~w
u
)P(z
u,n
= k|
~
θ
u
)
=
K
∑
k=1
P(i|z
u,n
= k, w
u,n−1
)ϑ
u,k
=
K
∑
k=1
ϕ
k, j,i
· ϑ
u,k
(10)
ProbabilisticSequenceModelingforRecommenderSystems
79

Table 2: Summary of the evaluation data.
IPTV1 IPTV2
Training Test Training Test
Users 16,237 16,153 64,334 63,878
Items 759 731 2802 2777
Evaluations 314,042 78,557 1,224,790 306,271
Avg # evals (user) 19 5 19 5
Avg # evals (item) 414 107 437 110
Min # evals (user) 4 1 4 1
Min # evals (item) 5 1 5 1
Max # evals (user) 252 15 497 17
Max # evals (item) 2284 1527 9606 3167
where j = w
u,n−1
is the last item selected by user
u in her current history.
3 EXPERIMENTAL EVALUATION
In this section we present an empirical evaluation of
the proposed models which focuses on the recom-
mendation problem. Given the past observed prefer-
ences of a users, the goal of a recommender systems
(RS) is to provide her with personalized (and con-
textualized) recommendations about previously non-
purchased items that meet her interest. Note that, al-
though usually the standard benchmarks for evaluat-
ing recommendations are Movielens and Netflix data,
they do not guarantee that the timestamp associated
with each pair huser, itemi corresponds to the times-
tamp of the effective purchase of the item, since the
timestamp refers to the rating and the user may spec-
ify ratings in a different order. Moreover, we cannot
rely on Videolectures data because, due to the pri-
vacy preserving constraints, this dataset do not pro-
vide user profiles but pooled statistics. We choose
to evaluate the performances of the proposed tech-
niques by measuring their predictive capabilities on
two datasets, namely Iptv1 and Iptv2. These data
have been collected by analyzing the pay-per-view
movies purchased by the users of two European IPTV
providers over a period of several months (Cremonesi
and Turrin, 2009; Bambini et al., 2011). The orig-
inal data have been preprocessed by firstly remov-
ing users with less of 10 purchases the items with
less then the same operation was performed over the
items. We perform a chronological split of the data
by including in the test set the last 20% purchases
of each user. The main features of the datasets are
summarized in Tab. 2. For each dataset, the users
and items, in the test data, are subsets of the users
and items within the training data. The sparseness
factors of Iptv1 are 97.5% and 99.3% for the train-
ing and test sets (resp.), while the ones for Iptv2 are
99.3% and 99.8% (training and test sets, resp.). These
values highlight the difficulty in discovering patterns
and regularities within the data, in other words it’s
hard to define a good model for the recommendation.
Fig. 2 and Fig. 3 show the distribution of the users
and the bigrams (resp.) for both the datasets. As can
be seen, these distributions exhibit the trend of power-
laws (Clauset et al., 2007).
Testing Protocol. Given an active user u and a con-
text c
u
currently under examination, the goal of a RS
is to provide u with a recommendation list R , picked
from a list C of candidates, that are expected to be of
interest to u. This clearly involves predicting the in-
terest of u into an item according to c
u
. We review
here the evaluation metrics and the testing protocols
to be used on this purpose.
In general, a recommendation list R can be gen-
erated as follows:
• Let C be a set of d candidate recommenda-
tions to arbitrary items;
• Associate each item i ∈ C with a score p
i
u,c
u
representing u’s interest into i in accordance
to context c
u
.
• Sort C in descending order of item scores
p
i
u,c
u
;
• Add the first k items from C to R and return
the latter to user u.
A common framework in the evaluation of the pre-
dictive capabilities of a RS algorithm is to split the
traces W into two subsets T and S, such that the for-
mer is used to train the RS, while the latter is used
for validation purposes. Here, for a given user, c
u
can
be defined according to the technique under examina-
tion: the set of previously unseen items for the LDA,
or the most recent preference for the Token-Bigram
model.
In the latter model, it is required that all sequences
in T precede those in S, in order to provide a fair sim-
ulation of real-life scenarios. As a consequence, for
a given user u, the trace ~w
u
can be split into ~w
(T )
u
and ~w
(S)
u
, representing the portions of the sequence
belonging to T and S, respectively. By selecting a
user u, the set C of candidate recommendations are
evaluated assuming ~w
(T )
u
part of the context. The rec-
ommendation list R for u is then formed by following
the foregoing generation process and the accuracy of
R is ultimately assessed through a comparison with
the items appearing in ~w
(S)
u
. Therein, the standard
classification-based metrics, i.e., precision and recall,
can be adopted to evaluate the recommendation accu-
KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
80

●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●●
●●
●
●
●
●
●
●
●
●
●
●●
●●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●●
●
●
●
●●
●
●
●
●
●●●
●
●
●
●●●
●●
●
●
● ●
●
●●●● ●●● ● ●● ●
IPTV1
Number of Actions
Number of Users
10 10
2
1
10 10
2
10
3
(a)
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●●
●●
●
●
●
●
●
●
●
●●
●
●●
●
●●●
●
●
●
●
●
●
●
●●
●●●●
●
●
●
●●●
●
●
●
●
●
●●
●
●
●
●●
●●
●
●●●●
●
●
●
●●
●●
●
●
●
●●
●
●●
●
●●
●
●
●
●
●
●●●●
●
●●●
●●
●●●●●●●
●
●●
●
●●●●●●●●●●●●●●●●●● ●
IPTV2
Number of Users
Number of Users
10 20 30 60 100 200 400
1
10 10
2
10
3
10
4
(b)
Figure 2: Distribution of the number of evaluation per user on both datasets.
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●●●●
●
●
●
●
●●
●
●
●●
●
●
●●
●
●
●●●●●
●
●
●●
●
●
●
●
●●●●
●
●
●
●
●●
●
●
●
●●●●●●●●●●●●
●
●●
●
●●●●● ●●●●●● ●●
●
●● ●
IPTV1 − Bigrams
Number of Occurrences
Number of Bigrams
1
10 10
2
10
3
1
10 10
2
10
3
10
4
10
5
(a)
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●●
●
●
●●
●●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●●
●●
●
●
●
●
●
●●●●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●●●
●●
●
●
●●
●●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●●
●
●●●●
●
●●●●●
●
●
●
●
●●
●
●
●
●
●
●●
●
●
●
●
●●
●
●
●
●
●●
●
●●●●●●
●
●●
●
●
●
●●●
●
●
●
●●●●●
●
●
●
●
●●
●●●
●
●●●●●
●
●
●●●●
●
●
●
●●
●
●●
●
●●●
●
●●●
●●
●●●●●●●●●●●●●●●●
●●
●●●●●●●●●●
●
●●●●●●●●●●●●●●●●●●●●●●
●
●●●●●●●●●●●●● ● ●● ●●●●●●●●
IPTV2 − Bigrams
Number of Occurrences
Number of Bigrams
1
10 10
2
10
3
1
10 10
2
10
3
10
4
10
5
(b)
Figure 3: Distribution of the number of bigrams on both datasets.
racy of R .
The latter can be defined according to an adap-
tation of the testing protocol defined in (Cremonesi
et al., 2010).
• For each user u and for each item i ≡ w
u,n
relative to a position n of ~w
(T )
u
:
– Generate the candidate list C by ran-
domly drawing from I − {i}.
– Add i to C .
– Associate each item j ∈ C with the score
rank(i,u) and sort C in descending order
of item scores.
– Consider the position of the item i in the
ordered list: if i belongs to the top-k
items, there is a hit; otherwise, there is
a miss.
By definition, recall for an item can be either 0
(in the case of a failure) or 1 (in the case case of a
hit). Likewise, precision can be either 0 (in the case
of a failure) or
1
k
(in the case of a hit). The overall
precision and recall are defined in (Cremonesi et al.,
2010) as the below averages:
Recall(k) =
#hits
|T|
Precision(k) =
#hits
k · |T|
=
recall(k)
k
A key role in the process of generating accurate
recommendation lists is played by the schemes with
which to rank items candidate for recommendation.
(Barbieri and Manco, 2011) provides a comparative
analysis of three possible such schemes, and studies
their impact in the accuracy of the recommendation
list. It is worth noting that the score rank(i, u) pro-
posed here follows the main findings in that paper.
Also, (Barbieri and Manco, 2011) shows that item
selection plays the most important role in recommen-
dation ranking. As a matter of fact, LDA turns out to
be the model that best accommodates item selection
in recommendation ranking, thus providing the best
recommendation accuracy according to the above de-
scribed protocol. It is natural hence to compare the
ProbabilisticSequenceModelingforRecommenderSystems
81
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Recall
Length of the Recommendation List
Recall on Iptv1
LDA(30) TokenBigram(30)
(a)
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Precision
Length of the Recommendation List
Precision on Iptv1
LDA(30) TokenBigram(30)
(b)
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0.55
0.6
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Recall
Length of the Recommendation List
Recall on Iptv2
LDA(30) TokenBigram(5)
(c)
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Precision
Length of the Recommendation List
Precision on Iptv2
LDA(30) TokenBigram(5)
(d)
Figure 4: Recommendation accuracy: LDA vs Sequence-based Approaches.
Token-Bigram model proposed in this paper with the
LDA approach.
Implementation Details. All the considered model
instances were run varying the number of topics
within the range [3, 20]. We perform 5000 Gibbs Sam-
pling iterations, discarding the first 1000 (burn in pe-
riod), and with a sample lag of 30.
Our implementations are based on asymmetric
Dirichlet prior over the document-topic distributions
(this modeling strategy has reported to achieve im-
portant advantages over the symmetric version (Wal-
lach et al., 2009)), while we employ a symmetric prior
over the topic distributions. For the LDA and token-
bigram models we adopted the procedure for updating
the prior
~
α as described in (Heinrich, 2008; Minka,
2000). We set the length of the candidate random list
(see the testing protocol) equal to about the 35% of
the dimension of the item sets for each test set. Pre-
cisely, these lists have 250 items for Iptv1 and 1000
items for Iptv2.
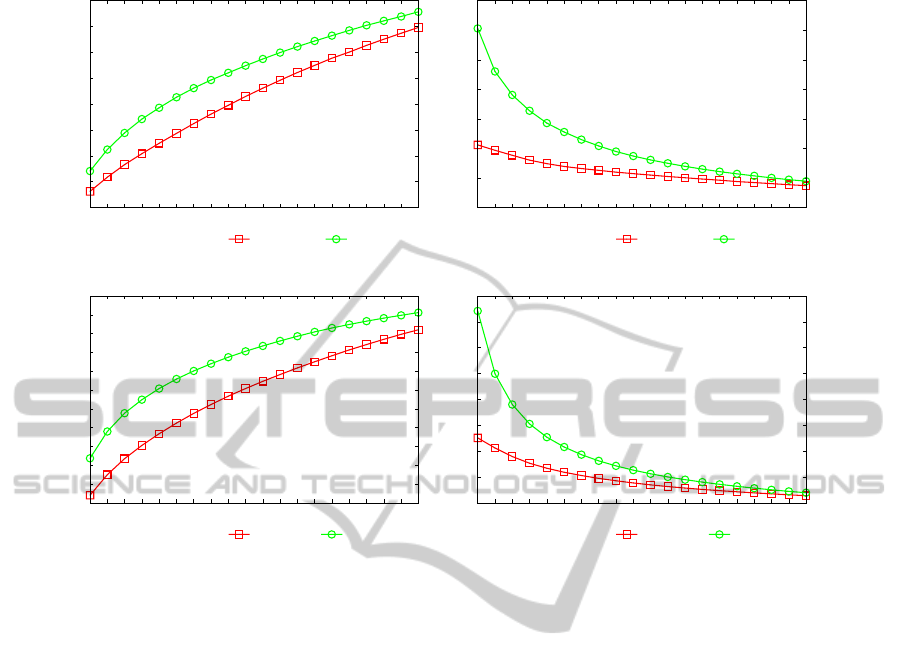
Results. In Fig. 4 we summarize the best results in
recommendation accuracy achieved by the proposed
approach, over the two considered datasets. For each
model, the number of topics which leads to the best
results is given in brackets. On both datasets, the
Token-Bigram models outperform the LDA models,
both in recall and precision. At high level, these re-
sults suggest that exploiting the previous contextual
information, the Token-Bigram Model outperforms
LDA in recommendation accuracy. While the ranking
function employed for LDA takes into account only
the probability of selecting an item given the whole
user purchase-history and the whole topic space, the
Token-Bigram approach focuses on a region of the
topic space determined by considering the previous
item, thus providing a better estimate of the selection
probabilities for the next user’s choice.
In order to assess the stability of the proposed ap-
proaches in varying the number of topics, we plot in
Fig. 5 and Fig. 6 the recall and the precision (respec-
tively) achieved when the length of the recommen-
dation list is 20. Considering Iptv1, best results are
achieved by both the techniques exploiting the largest
number of topics we used for the experimentation, 30,
with a recall of 0.347 and a precision of 0.017 for
LDA and a recall of 0.379 and a precision of 0.019
for the Token Bigram, with a difference in recall of
0.032. For Iptv2, LDA achieves its maximum one
again with 30 topics, while the proposed model has
the best quality with 5 topics. LDA achieve a recall
KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
82
0.3
0.31
0.32
0.33
0.34
0.35
0.36
0.37
0.38
3 5 7 10 20 30
Recall(20)
Number of Topics
Recall(20) on Iptv1
LDA TokenBigram
(a)
0.015
0.0155
0.016
0.0165
0.017
0.0175
0.018
0.0185
0.019
3 5 7 10 20 30
Precision(20)
Number of Topics
Precision(20) on Iptv1
LDA TokenBigram
(b)
Figure 5: Recall(20) of the considered approaches varying the number of topics on IPTV1
0.38
0.4
0.42
0.44
0.46
0.48
0.5
0.52
0.54
0.56
3 5 7 10 20 30
Recall(20)
Number of Topics
Recall(20) on Iptv2
LDA TokenBigram
(a)
0.019
0.02
0.021
0.022
0.023
0.024
0.025
0.026
0.027
0.028
3 5 7 10 20 30
Precision(20)
Number of Topics
Precision(20) on Iptv2
LDA TokenBigram
(b)
Figure 6: Precision(20) of the considered approaches varying the number of topics on IPTV2.
0
20
40
60
80
100
120
3 5 7 10 20 30
Time(mins)
Number of Topics
Learning Time on Iptv1
LDA
Token
(a)
0
50
100
150
200
250
300
350
400
3 5 7 10 20 30
Time(mins)
Number of Topics
Learning Time on Iptv2
LDA
Token
(b)
Figure 7: Learning time of the models.
and a precision of 0.512 and 0.026 (resp.), while the
Token Bigram has 0.556 for recall and 0.028 for pre-
cision, with a difference in recall of 0.044.
It’s interesting to note that the performances of the
TokenBigram do not change substantially varying the
number of topics. The results presented above exper-
imentally prove the effectiveness of sequence-based
topic models in modeling and predicting future users’
choices. However those models increase significantly
the number of parameters to be learned and this im-
plies an increase in the learning time. In Fig. 7 we plot
the learning time (5000 Gibbs Sampling iterations)
for different numbers of topics. The learning time is
consequently considerably larger. This is mainly due
to the larger number of hyperparameters (K ×K vs K)
and to the complexity of the α-update iterative proce-
dure.
ProbabilisticSequenceModelingforRecommenderSystems
83

4 CONCLUSIONS AND FUTURE
WORKS
In this paper we proposed an extension of the LDA
model. The proposed model relaxes the bag-of-words
assumption of LDA, assuming that each token, not
only depends on a number of latent factors, but also
on the previous token. The set of dependencies has
been modeled as a stationary Markov chain, which
led us to define a procedure for estimating the model
parameters, exploiting the Gibbs Sampling. This
model better suites a framework for modeling con-
text in a recommendation setting than LDA, since
it takes into account the information about the to-
ken sequence. The experimental evaluation, over two
real-world datasets expressing sequence information,
shows that the proposed model outperforms LDA at
the expense of an higher execution time when the
number of the latent topics is large, since the num-
ber of parameters to estimate is bigger than in LDA.
In the future we are going to investigate more kinds of
Markov chains expressing the sequence of the tokens,
moreover we have the intention of improving the pro-
posed model by considering side information such as
tags or comments over tokens.
REFERENCES
Bambini, R., Cremonesi, P., and Turrin, R. (2011). A
recommender system for an iptv service provider: a
real large-scale production environment. In Ricci,
F., Rokach, L., Shapira, B., and Kantor, P. B., ed-
itors, Recommender Systems Handbook, pages 299–
331. Springer.
Barbieri, N., Costa, G., Manco, G., and Ortale, R. (2011a).
Modeling item selection and relevance for accurate
recommendations: a bayesian approach. In Proc. Rec-
Sys, pages 21–28.
Barbieri, N. and Manco, G. (2011). An analysis of prob-
abilistic methods for top-n recommendation in col-
laborative filtering. In Proceedings of the 2011 Eu-
ropean conference on Machine learning and knowl-
edge discovery in databases - Volume Part I, ECML
PKDD’11, pages 172–187.
Barbieri, N., Manco, G., Ortale, R., and Ritacco, E.
(2011b). Balancing prediction and recommendation
accuracy: Hierarchical latent factors for preference
data. In Proc. SDM’12.
Bishop, C. (2006). Pattern Recognition and Machine
Learning. Springer.
Blei, D. M., Ng, A. Y., and Jordan, M. I. (2003). Latent
dirichlet allocation. The Journal of Machine Learning
Research, 3:993–1022.
Cadez, I., Heckerman, D., Meek, C., Smyth, P., and White,
S. (2000). Visualization of navigation patterns on a
web site using model-based clustering. In Proceed-
ings of the sixth ACM SIGKDD international confer-
ence on Knowledge discovery and data mining, KDD
’00, pages 280–284.
Clauset, A., Shalizi, C., and Newman, M. E. J. (2007).
Power-law distributions in empirical data. SIAM Re-
views.
Cremonesi, P., Koren, Y., and Turrin, R. (2010). Perfor-
mance of recommender algorithms on top-n recom-
mendation tasks. In ACM RecSys, pages 39–46.
Cremonesi, P. and Turrin, R. (2009). Analysis of cold-start
recommendations in iptv systems. In Proceedings of
the third ACM conference on Recommender systems,
RecSys ’09, pages 233–236. ACM.
Griffiths, T. L., Steyvers, M., and Tenenbaum, J. B. (2007).
Topics in semantic representation. Psychological Re-
view 114.
Gruber, A., Weiss, Y., and Rosen-Zvi, M. (2007). Hidden
topic markov models. Journal of Machine Learning
Research, 2:163–170.
Heinrich, G. (2008). Parameter Estimation for Text Analy-
sis. Technical report, University of Leipzig.
Minka, T. P. (2000). Estimating a Dirichlet distribution.
Technical report, Microsoft Research.
Wallach, H., Mimno, D., and McCallum, A. (2009). Re-
thinking lda: Why priors matter. In Bengio, Y., Schu-
urmans, D., Lafferty, J., Williams, C. K. I., and Cu-
lotta, A., editors, Advances in Neural Information
Processing Systems 22, pages 1973–1981.
Wallach, H. M. (2006). Topic modeling: beyond bag-of-
words. In Proceedings of the 23rd international con-
ference on Machine learning, ICML ’06, pages 977–
984.
X. Wang, A. M. and Wei, X. (2007). Topical n-grams:
Phrase and topic discovery, with an application to in-
formation retrieval. In Procs. ICDM’07, pages 697–
702.
KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
84
