
Issues of Optimization of a Genetic Algorithm for Traffic Network
Division using a Genetic Algorithm
Tomas Potuzak
Department of Computer Science and Engineering, University of West Bohemia, Univerzitni 8, Plzen, Czech Republic
Keywords: Genetic Algorithm, Traffic Network Division, Parameters Optimization.
Abstract: In this paper, we describe an approach to optimization of the genetic algorithm for division of road traffic
network, which we developed. The division of road traffic network is necessary to enable to perform the
road traffic simulation in a distributed computing environment. The optimization approach is based on a
genetic algorithm, which is employed to find best settings of the optimized genetic algorithm for road traffic
network division. Because such an optimizing genetic algorithm is expected to be extremely computation-
and time-consuming, its distributed implementation is discussed as well.
1 INTRODUCTION
Utilization of a distributed computing environment,
where combined power of multiple interconnected
computers (nodes) is utilized, is a common way how
to speed up a detailed simulation of road traffic.
Prior to the distributed simulation itself, the
simulated road traffic network must be divided into
sub-networks, which are then simulated on particular
nodes of a distributed computer. To achieve a good
speedup of the simulation, two issues should be
considered during the division – the load-balancing
of the resulting sub-networks and the minimization
of the inter-process communication.
In our previous work, we have developed a
method for division of road traffic network based on
a genetic algorithm, which considers both the
mentioned issues (Potuzak, 2011b). The method
gives good results (Potuzak, 2012). However, the
parameters of the genetic algorithm have been set
manually based on preliminary testing. Hence, it is
likely that the settings of the parameters are not
optimal and can be tuned to achieve better
performance of the division method.
In this paper, we discuss the usability of a
genetic algorithm for optimization of the parameters
of the genetic algorithm for road traffic network
division, which we developed. Because the
optimizing genetic algorithm is expected to be
extremely computation- and time-consuming, we
discuss its distributed implementation as well.
2 GENETIC ALGORITHMS
Genetic algorithms are evolutionary algorithms,
which mimic natural genetic evolution and selection
in nature in order to solve a problem. Developed by
John Holland in 1975 (Holland, 1975), they are
widely used for solving of optimization and
searching problems in many domains, including
multi-objective optimization (Farshbaf and Feizi-
Darakhshi, 2009).
2.1 Basic Notions of Genetic Algorithm
There are several basic phases and notions, which
are commonly present using a typical genetic
algorithm.
A single solution of the solved problem is
considered to be an individual (usually represented
by a vector of binary or integer values). At the start,
a set of individuals (so-called initial population) is
most often randomly generated (Menouar, 2010).
Then, the fitness function is calculated for each
individual. The fitness function represents an
objective assessment of each individual depending
on the solved problem. Then, a number of indivi-
duals with highest fitness value are selected as the
parents of a new generation. The new generation is
created using the selected individuals and the
crossover and mutation operators (Menouar, 2010).
The entire process repeats until a preset number
of generations is created or a stop condition is met.
340
Potuzak T..
Issues of Optimization of a Genetic Algorithm for Traffic Network Division using a Genetic Algorithm.
DOI: 10.5220/0004141803400343
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2012), pages 340-343
ISBN: 978-989-8565-29-7
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

3 GA NETWORK DIVISION
The method for division of road traffic network,
which we developed, is based on a genetic
algorithm. It will be briefly described in this section.
3.1 Issues of Network Division
There are two issues, which should be considered
during the road traffic network division – the load-
balancing of the resulting sub-networks and the
minimization of the inter-process communication.
The load-balancing is necessary in order to
maximally utilize the computational power of all
nodes of the distributed computer. The minimization
of the inter-process communication, which is used
for the transfer of vehicles among the sub-networks
and for the synchronization, is necessary, since it is
much slower than the reminder of the simulation
computations.
3.2 Description of Division Method
The method for road traffic network division, which
we developed, considers both the load-balancing of
the sub-networks and the minimization of the inter-
process communication. It utilizes a less-detailed
road traffic simulation for assigning of the weights
to particular traffic lanes (Potuzak, 2011a). These
weights correspond to the numbers of vehicles
moving in particular lanes of the divided road traffic
network (Potuzak, 2012).
Once the weights are assigned, the traffic
network can be considered as a weighted graph with
traffic crossroads acting as nodes and the sets of
lanes connecting particular traffic crossroads acting
as weighted edges (with weights equal to sum of
weights of particular traffic lanes of the set). The
road traffic network (i.e. weighted graph) is then
divided using a genetic algorithm (GA) into required
number of load-balanced sub-networks with minimal
number of divided traffic lanes.
An individual of the utilized genetic algorithm
represents a single assignment of the crossroads to
particular sub-networks. The fitness function
consists of two parts – the equability representing
the load-balancing and the compactness representing
the minimization of inter-process communication.
The ratio of these two parts can be changed, but is
set to 0.75 in favour of the equability by default.
Each generation has 90 individuals, from which 10
individuals with highest fitness value are selected to
be parents of the next generation. The crossover is
performed using each combination of two parents
producing two offspring. Each offspring can be
mutated using up to five random changes. The entire
process repeats for preset number (from 1000 to
100 000) of generations (Potuzak, 2011b).
4 OPTIMIZING GA USING GA
The values of particular parameters of the genetic
algorithm were set based on preliminary testing. So,
it is possible that the settings are not optimal. Hence,
we utilize another genetic algorithm for the
optimization of the particular parameters of the
genetic algorithm for road traffic network division.
The genetic algorithm for optimization of the
parameters of the genetic algorithm for road traffic
network division will be referred as optimizing
genetic algorithm or OGA further in the text.
4.1 Parameters of GA to Optimize
The most obvious parameters of the genetic
algorithm for road traffic network division, which
should be optimized, are the number of individuals
in a generation, the number of individuals selected
based on the fitness function, and the number of
generations. Another parameter, which can be
optimized, is the maximal number of mutations (i.e.
random changes), which can be applied to each
individual during the creation of a new generation.
Besides the mutation, the crossover and selection
of the parent individuals can be considered for the
optimization as well. In our genetic algorithm for
road traffic network division, only one type of
selection (simple truncation selection) and one type
of crossover (see Section 3.2) have been employed.
However, there are more types of selection and
crossover, which can be utilized as well. For
example, the fitness proportionate approach (Bäck,
1996) or the reward-based approach (Loshchilov et
al., 2011) can be used for selection. For the
crossover, one-point or two point segment approach
or the uniform crossover can be utilized (Ahmed,
2010).
The parameter, which will not be optimized, is
the ratio in the fitness function (see Section 3.2) due
to its direct influence on the quality of the road
traffic network division.
4.2 OGA Individual Representation
The representation of an individual of the OGA must
incorporate all parameters described in previous
section. All the parameters can be expressed as
IssuesofOptimizationofaGeneticAlgorithmforTrafficNetworkDivisionusingaGeneticAlgorithm
341

integer numbers but of different maximal size.
Hence, the bits of particular integer values will be
used in the individual directly. More specifically,
each individual will consist of 52 bits. First 20 bits
will be used for number of generations (i.e. 0 to
1 048 576 generations), 10 bits for number of
individuals in one generation (i.e. 0 to 1024 indivi-
duals), 10 bits for number of selected individuals
from each generation (i.e. 0 to 1024 individuals), 8
bits for maximal number of mutations per individual
(i.e. 0 to 256 mutations), 2 bits for type of selection
(i.e. up to 4 types of selection), and 2 bits for type of
crossover (i.e. up to 4 types of crossover). An
example is depicted in Fig. 1.
Figure 1: Example of an OGA individual.
The initial population will consist of 90
individuals (similar to the optimized genetic
algorithm for road traffic network division), which
will be randomly generated. Although a larger
number of individuals could be more appropriate,
we have to have in mind that the OGA will be
extremely time-consuming and the computation time
would increase with increasing number of
individuals in one generation.
4.3 OGA Fitness Function
The OGA fitness function will be calculated for all
individuals. For each OGA individual, the
parameters of the genetic algorithm for road traffic
network division will be set accordingly. Then, 3
road traffic networks (regular grids of 64, 256, and
1024 crossroads) will be divided into 2, 4, 8, and 16
sub-networks. So, 12 complete optimized genetic
algorithms will be used for each OGA individual to
keep the optimization as universal as possible.
The OGA fitness function will be then calculated
using the maximal achieved fitness values for each
combination of the divided network and the number
of sub-networks as:
12
3
1
4
1
max
ij
ij
OGA
F
F
,
(1)
where F
OGA
is the OGA fitness function,
max
ij
F is the
maximal achieved fitness function of the optimized
genetic algorithm for ith traffic network and jth
number of sub-networks.
4.4 OGA Selection
Once the fitness value will be calculated for every
individual of the current generation, 10 individuals
with highest fitness value of the 90 individuals of the
current generation (see Fig. 2) will be selected to be
parents of next generation. This selection is the same
as the one used in the optimized genetic algorithm
for road traffic network division (Potuzak, 2012).
Figure 2: Simple truncation selection used in OGA.
4.5 OGA Crossover and Mutation
Once the parents are selected, a new generation is
produced using the crossover and mutation in the
same way as in the optimized genetic algorithm for
road traffic network division (see Fig. 3).
Figure 3: Crossover of two individuals and four mutations.
Using the crossover and mutation, a new
generation is produced. The entire process then
repeats until the preset number of generations is
reached. Since the OGA is very computation- and
time-consuming (see Section 5), the number of
created generations will be limited by the
computational power and time at our disposal.
4.6 Distributed OGA
To achieve a feasible computation time, the OGA
will be performed on a distributed computer
consisting of 24 desktop PCs. Each PC incorporates
one Intel i5-2400S Quad-Core processor at 3.1 GHz,
8 GB of RAM, and 250 GB HDD.
The calculation of the fitness value is by far the
most time-consuming part of the OGA (see
Section 4.3). Hence, the individuals of an OGA
generation will be uniformly distributed among all
available processor cores where the fitness values
will be calculated by working processes. The
selection, crossover, and mutation will be then
performed by a control process.
KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
342
5 TESTS AND RESULTS
In order to predict the feasibility of the distributed
OGA and its time requirements, we have performed
a set of tests. These tests were performed directly on
one of the computers, on which the distributed OGA
is planned to be performed (see Section 4.6). On the
computer, the DUTS Editor, which is a system
containing implementation of the optimized genetic
algorithm for road traffic network division, was
installed together with the described road traffic
networks (see Section 4.3). Then, the networks were
divided into four (one of the four numbers of sub-
networks used by the OGA – see Section 4.3) sub-
networks using from 1000 to 1 000 000 generations
of the optimized genetic algorithm.
In order to test the usability of multiple cores
simultaneously, the division was performed on one
and four cores. The results are depicted in Table 1.
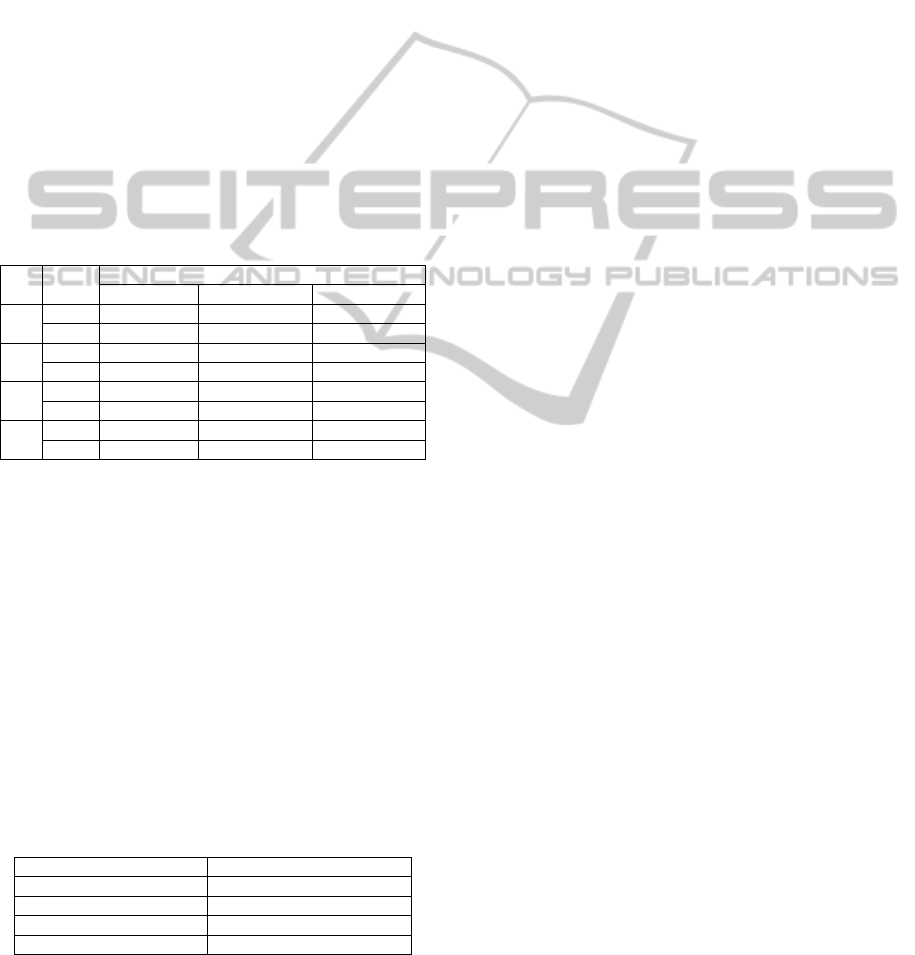
Table 1: Results of the testing.
Gen. Cores
Computation time [ms]
64 crossroads 256 crossroads 1024 crossroads
10
3
1 830 3296 15310
4 859 3631 15834
10
4
1 7982 32859 139753
4 8699 35825 149127
10
5
1 79661 320038 1396286
4 86248 348558 1492700
10
6
1 805411 3063346 12309876
4 853462 3499342 14851707
As can be seen in Table 1, the simultaneous
usage of more cores increases the computation time,
but only by roughly 7 %. Hence, it is possible to
utilize all four cores simultaneously.
The time necessary for calculation of the fitness
value of an OGA individual is the sum of the times
necessary for division of particular networks into 2,
4, 8, and 16 sub-networks (i.e. four times sum of one
row of Table 1). Considering simultaneous usage of
all cores, the total time necessary for computation of
the fitness value of one OGA individual using one
core is summarized in Table 2 in the dependency on
the number of generations of the optimized genetic
algorithm for road traffic network division.
Table 2: Computation of an OGA individual fitness value.
Number of generations Computation time [ms]
1000 81296
10000 774608
100000 7710024
1000000 76818044
6 CONCLUSIONS
In this paper, we described the OGA and its possible
distributed implementation for multi-core personal
computers. Considering usage of 24 quad-core
computers (i.e. 96 cores), the predicted computation
time of the OGA ranges from 21 to 2 · 10
6
hours
depending on the number of generations of the OGA
and the optimized genetic algorithm. Hence, only
lower numbers of generations are feasible.
In our future work, we will focus on implemen-
tation of the distributed OGA and its testing.
ACKNOWLEDGEMENTS
Author wishes to thank to Jakub Smid for the
inspiration for the main idea of this paper.
REFERENCES
Ahmed, Z. H., 2010. Genetic Algorithm for the Traveling
Salesman Problem Using Sequential Constructive
Crossover Operator. In International Journal of
Biometric and Bioinformatics, vol. 3(6), pp. 96–105.
Bäck, T., 1996. Evolutionary algorithms in theory and
practice: evolution strategies, evolutionary
programming, genetic algorithms. Oxford University
Press, New York.
Farshbaf, M., Feizi-Darakhshi, M., 2009. Multi-objective
Optimization of Graph Partitioning using Genetic
Algorithms. In: 2009 Third International Conference
on Advanced Engineering Computing and
Applications in Sciences.
Holland, J. H., 1975. Adaptation in Natural and Artificial
Systems. University of Michigan Press, Ann Arbor.
Loshchilov, I., Schoenauer, M., Sebag, M., 2011. Not all
parents are equal for MO-CMA-ES. In Evolutionary
Multi-Criterion Optimization 2011 (EMO 2011),
Springer Verlag, LNCS 6576. pp. 31–45.
Menouar, B., 2010. Genetic Algorithm Encoding
Representations for Graph Partitioning Problems. In:
2010 International Conference on Machine and Web
Intelligence (ICMWI), pp. 288–291.
Potuzak, T., 2011. Usability of Macroscopic and
Mesoscopic Road Traffic Simulations in Division of
Traffic Network for Distributed Microscopic
Simulation. In CSSim 2011, Brno, pp. 94–101.
Potuzak, T., 2011. Suitability of a Genetic Algorithm for
Road Traffic Network Division. In KDIR 2011, Paris,
pp. 448–451.
Potuzak, T., 2012. Methods for Division of Road Traffic
Networks Focused on Load-Balancing. In Advances in
Computing, submitted for publication.
IssuesofOptimizationofaGeneticAlgorithmforTrafficNetworkDivisionusingaGeneticAlgorithm
343
