
A Hybrid Solution for Imbalanced Classification Problems
Case Study on Network Intrusion Detection
Camelia Lemnaru, Andreea Tudose-Vintila, Andrei Coclici and Rodica Potolea
Technical University of Cluj-Napoca, 26-28 Barițiu Street, Cluj-Napoca, Romania
Keywords: Imbalanced Multi-class Classification, Multiple Classifier, Prediction Combination, Anomaly Detection,
KDD’99 Data.
Abstract: Imbalanced classification problems represent a current challenge for the application of data mining
techniques to real-world problems, since learning algorithms are biased towards favoring the majority
class(es). The present paper proposes a compound classification architecture for dealing with imbalanced
multi-class problems. It comprises of a two-level classification system: a multiple classification model on
the first level, which combines the predictions of several binary classifiers, and a supplementary
classification model, specialized on identifying “difficult” cases, which is currently under development.
Particular attention is allocated to the pre-processing step, with specific data manipulation operations
included. Also, a new prediction combination strategy is proposed, which applies a hierarchical decision
process in generating the output prediction. We have performed evaluations using an instantiation of the
proposed model applied to the field of network intrusion detection. The evaluations performed on a dataset
derived from the KDD99 data have indicated that our method yields a superior performance for the minority
classes to other similar systems from literature, without degrading the overall performance.
1 INTRODUCTION
In a real data mining application setting, cases of
interest are more difficult to collect, resulting in
imbalanced datasets. This represents a major issue,
since traditional classifiers expect balanced class
distributions. An imbalanced class distribution
causes the minority class to be treated as noise, the
classification process achieving little or no detection
of it (He, 2009). Several different strategies for
improving the behaviour of classifiers in imbalanced
domains have been reported. Broadly, the
approaches for dealing with imbalanced problems
are split into (Galar, 2011): data-centered based on
sampling methods, algorithm-centered and hybrid
solutions.
The strategy we propose in this paper falls into
the hybrid systems category. It comprises of a
multiple classifier system, which employs different
binary classification sub-models, sampling to obtain
the appropriate volume and class distribution for
training each sub-model, intelligent voting strategies
and an additional classification stage for the
instances which failed to be classified by the
previous steps.
The rest of the paper is organized as follows:
Section 2 presents the proposed solution, followed
by a case study on network intrusion detection in
Section 3. Section 4 discusses concluding remarks.
2 PROPOSED SOLUTION
The learning model proposed in this paper addresses
the classification of multi-class problems having
highly imbalanced class distribution, with one class
(which we further name the majority class) being
significantly better represented in comparison with
the other classes (further named minority classes).
The main goal of such problems is to obtain a high
performance in detecting the minority classes,
without degrading the overall classification rate.
The approach we propose is based on a hybrid
technique, more specifically it is a multiple classifier
system combined with a data pre-processing stage.
Multiple classification systems are designed in such
a way that the base classifiers compensate for each
other’s drawbacks. The resulting model possesses
increased robustness and generalization capabilities
348
Lemnaru C., Tudose-Vintila A., Coclici A. and Potolea R..
A Hybrid Solution for Imbalanced Classification Problems - Case Study on Network Intrusion Detection.
DOI: 10.5220/0004142803480352
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2012), pages 348-352
ISBN: 978-989-8565-29-7
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
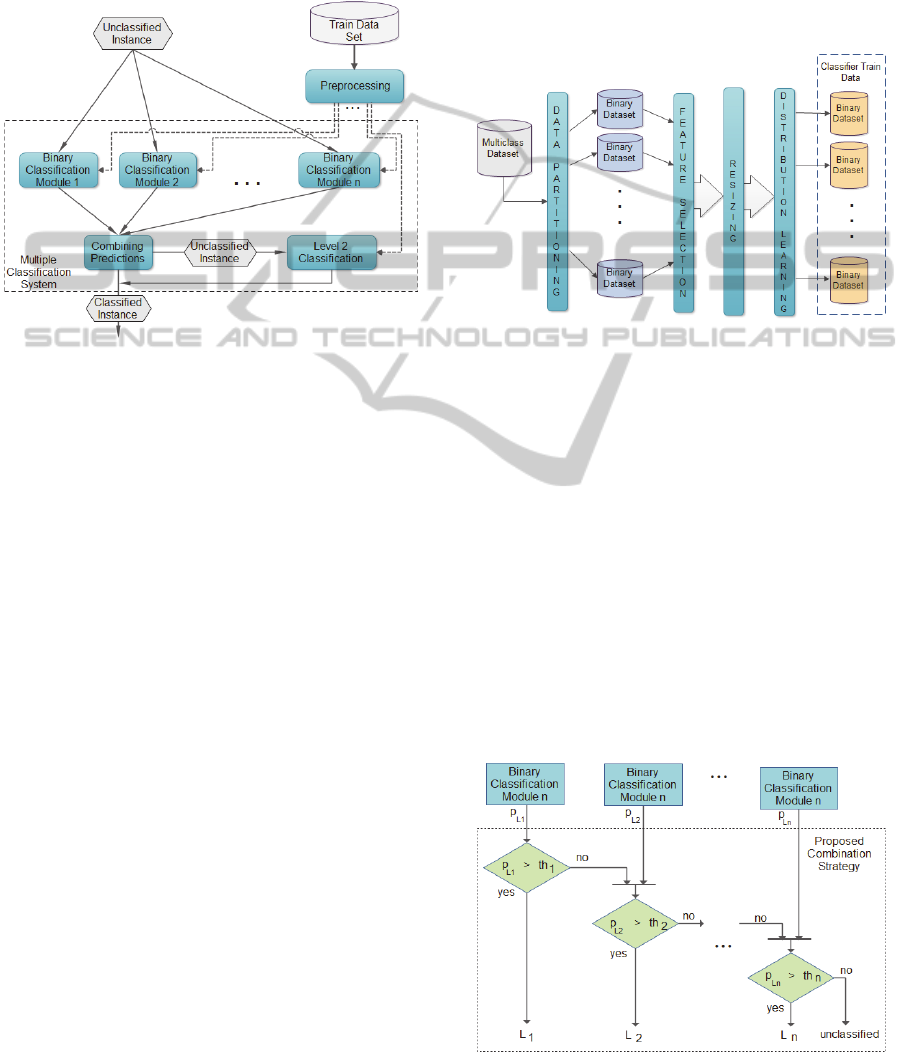
(Seni, 2010). The conceptual architecture of the
method is presented in the diagram from Figure 1.
The training flow starts with an initial data
preparation step. Each binary classification module
is specialized on correctly classifying a specific class
of interest, and possesses the highest performance
for that specific class.
Figure 1: Conceptual architecture.
The predictions obtained from the binary
classifiers are processed using a combiner module.
This module is based on a newly proposed method
for combining the individual predictions, depending
on the domain in which the problem of classification
resides. Instances which cannot be classified via this
mechanism (i.e. the voting strategy cannot indicate a
single output label) are delivered to the Level 2
classification module, which is targeted at
classifying “difficult” instances.
The pre-processing stage consists in the
successive application of a number of mechanisms
on the initial data. As shown in Figure 2, this stage
comprises of four main steps: data partitioning,
feature selection, resizing and learning the optimal
distribution. In the data partitioning step, the
available dataset is partitioned into several subsets,
each containing all the instances belonging to one
class. The one-class subsets are then merged to form
binary problems in one versus one (OvO) and one
versus all (OvA) fashion as seen in Figure 4. The
feature selection step is employed to remove
irrelevant and/or redundant attributes. It is
performed independently on each binary dataset,
thus resulting in a specialized training data for the
specific binary classification module. Each resulting
subset is expected to improve the robustness and
generalization capabilities of the subsequent learning
models.
The data resizing step applies sampling
strategies to determine the optimal volume for
training each binary classification module. It is
applied in conjunction with the optimal training
distribution learning step, which attempts to
determine the best learning distribution for each
individual binary module (Weiss, 2003). We expect
that the best learning distribution be influenced by
the performance metric employed.
Figure 2: Data pre-processing stage.
The binary classifiers training stage identifies
the best classification strategy for each individual
binary problem and performs parameter tuning for
the underlined classifier-dataset pair.
The predictions obtained from the binary
classifiers are combined by the prediction
combination module. The predictions are initially
ranked according to domain knowledge, data
distribution and the gravity of failing to identify a
specific class. Then, the instance to be classified is
presented, in turn, to each binary model, until one of
them produces a positive identification, i.e. the
probability that the instance belongs to the given
class is larger than the identification threshold value
as seen in Figure 3. The identification threshold
values are learned for each individual binary model.
Figure 3: Custom prediction combination strategy.
AHybridSolutionforImbalancedClassificationProblems-CaseStudyonNetworkIntrusionDetection
349

The Level 2 classification model is responsible
for solving difficult identification cases, more
specifically for attempting to classify instances
which have not been assigned a label by the multiple
classifier system. We propose the employment of a
one class learning approach, as the majority
instances are better represented and clustered, thus
being easier to model.
3 NETWORK INTRUSION
DETECTION CASE STUDY
(NID)
Dataset: The data employed to build the model for
the target problem is derived from the NSL-KDD
Dataset (Tavallaee, 2009), which is an improved 2-
class version of the KDD CUP ’99 Dataset
(Kristopher, 1999), having the following classes:
normal traffic and anomalous traffic. We have
grouped the dataset in the following five classes:
DoS (Denial of Service), Probe, R2L (Remote to
Local), U2R(User to Root), Normal.
The major challenge with the resulting training and
testing datasets is that they have imbalanced class
distributions. Figure 4 presents the number of
instances of each class in the training and testing
datasets. The imbalance ratio (IR) represents the
ratio between the number of instances belonging to
each of the attack classes and the normal class. We
will follow the previous design for a particular N=5,
corresponding to the 5 clases.
Evaluation: A first set of tests has been conducted
on a relabeled version of the NSL-KDD training set
in order to analyze the performance of different
classification methods on each type of attack. We
employed a 5-fold cross validation with default
parameter settings for classifiers and true positive
rate as performance metric. Although some
classifiers perform well for each binary problem, the
results have indicated that there is no single winning
classification strategy.
By comparing the number of true positives, the
following two classifiers for each binary problem
will be considered for further evaluations: REPTree
and RandomForest for DoS, Random Forest and
Naive Bayes Tree for Probe, Bayes Net and Naive
Bayes for R2L, Naive Bayes and Bayes Net for
U2R, Random Forest and Naive Bayes Tree for
Normal.
For the data resizing and distribution learning
steps, two different approaches have been explored:
simple re-sampling, by using random under-
sampling and oversampling, and smart re-sampling,
by using the SMOTE algorithm (Chawla, 2002).
Evaluations have been performed by varying the
distribution of the primary class from 10% to 90%,
with an increment of 10%, with the F
β
-measure as
evaluation metric: β=2 for the strongly represented
classes (DoS, Probe, Normal) and β=4 for the
weakly represented classes (R2L and U2R). The
results indicate that the distribution is strongly
dependent on the dataset and the learning method.
Figure 4: Data partitioning for NID data.
As smart re-sampling techniques only slightly
improve the performance of some classifiers,
considering the processing time, their employment
over simpler strategies is not justified.
Binary Model Tuning: Figure 5 presents the results
obtained for tuning the RandomForest classifier for
the Probe module. The curves in Figure 5 indicate
that selecting a small number of features increases
the recognition error for both classes involved (as
result of under-fitting). A similar effect is obtained
by considering a large number of features (as a result
of over-fitting).Thus, around 11 features is an
appropriate value for this parameter. Similarly, a
good value for the number of trees used in the
ensemble has been found to be around 16.
The best settings for the other modules are: DoS – 4
trees, 22 features for RandomForest; R2L and the
U2R –default BayesNet; Normal – 20 trees, 14
features for RandomForest.
Several different voting strategies have been
considered: majority voting (Maj), product voting
(Prod), average voting (Avg), maximum voting
(Max), median voting (Med) – all available in
WEKA (Witten , 2011) and our proposed cascading
voting strategy (Cas). The evaluation results are
presented in Table 1. Cas yields the best
identification for all attack classes, achieving an
KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
350

acceptable identification rate on the normal packets.
Figure 5: Variation of FP and FN with the number of
attributes for Random Forest, Probe module.
Table 1: TP, FN for different voting strategies.
DoS Probe R2L U2R Normal
TP FN TP FN TP FN TP FN TP FN
Maj 22587 4969 3814 3179 41 556 1 30 40401 4
Avg 22709 4847 3793 3200 43 554 1 30 40402 3
Max 27535 21 6761 232 462 135 5 26 40393 12
Med 6 0 22 0 25 0 11 0 0 40354
Prod 26869 20 3720 216 4 134 0 26 40393 11
Cas 27556 0 6981 12 593 4 28 3 39954 451
Although in our results we have not yet included
the Level 2 classifier, our preliminary experiments
indicate a Local Outlier Factor (LOF) (Breunig,
2000) approach to be the most promising. This
method is appropriate because normal points tend to
group into clusters of homogeneous density, whereas
attacks appear as outliers.
Evaluating the Overall System: All the
configurations previously identified are employed to
build the current version of our system. The results
obtained by evaluating the fully configured system
on the test dataset can be seen in the first column of
the Table 2. The results obtained by our system have
been compared to other systems evaluated on the
KDD’99 dataset. Our system yields significant
improvements in the detection of minority classes
compared to the other systems (Gogoi, 2010);
(Elkan, 2000): 90% correctly labeled instances for
the R2L class and 85% for the U2R.
Table 2: Recognition rates/classes.
Our System
KDD
Winner
Catsub FCM
SVM
+DGSOT
DoS 97% 97% 100% 99% 97%
Probe 100% 83% 37% 93% 91%
R2L 90% 8% 82% 83% 43%
U2R 85% 13% 0% 0% 23%
Normal 89% 99% 82% 96% 95%
4 CONCLUSIONS
To tackle imbalanced problems, we propose a two-
step hybrid classification model combined with a
pre-processing stage. In the first stage, a multiple
classifier which combines the predictions of several
binary base models is used. On the second one, an
additional classifier is employed, specialized on
classifying difficult instances. We also propose a
cascaded prediction combination approach, in which
the binary predictors are ranked and output their
predictions in turn, up to the point where a positive
identification is made.
We have applied our proposed system to a
network intrusion detection problem. We have
compared the results obtained by our system with
previous results on the same problem. We show that
our system achieves significantly higher
identification rates for the least represented classes
than the rest of the systems, without degrading the
identification of majority classes considerably.
REFERENCES
Breunig, M., Kriegel, H., P., Ng, R., Sander, J., 2000.
LOF: identifying density-based local outliers.
Proceedings of the 2000 ACM SIGMOD international
conference on Management of data, vol. 29, no. 2, pp.
93-104.
Chawla, N. V., Bowyer, K. W., Hall, L. O., Kegelmeyer,
W. P., 2002. SMOTE: Synthetic Minority Over-
Sampling Technique. Journal of Artificial Intelligence
Research, vol. 16, pp. 321-357.
Elkan, C., 2000. Results of the KDD’99 Clasiffier learnig.
SIGKDD Exploration, vol.1, no.2, pp. 63-64.
Galar, M., Fernandez, A., Barrenechea, E., Bustince,
Herrera, F., 2011. A Review on Ensembles for the
Class Imbalance Problem: Bagging-, Boosting-, and
Hybrid-Based Approaches. IEE transctions Systems,
Man, and Cybernetics, Part C: Applications and
Reviews, vol.42, no.4, pp. 463-484.
Gogoi, P., Borah, B., Bhattacharyya, D., K., 2010.
Anomaly Detection Analysis of Intrusion Data using
Supervised & Unsupervised Approach. Journal of
Convergence Information Technology, vol. 5, no. 1,
pp. 95-110.
He, H., Garcia, E. A., 2009. Learning from Imbalanced
Data. IEEE Transactions on Knowledge And Data
Engineering, vol. 21, no. 9, pp. 1263-1284.
Kristopher, K., 1999. A Database of Computer Attacks for
the Evaluation of Intrusion Detection Systems. Master
of Engineering on Electrical Engineering and
Computer Science, MIT.
Seni, G., Elder, J., Grossman, R., 2010. Ensemble Methods
in Data Mining: Improving Accuracy Through
AHybridSolutionforImbalancedClassificationProblems-CaseStudyonNetworkIntrusionDetection
351

Combining Predictions. Morgan & Claypool
Publishers.
Tavallaee, M,. Bagheri, M., Wei, L., Ghorbani, A. A.,
2009. A Detailed Analysis of the KDD CUP 99 Data
Set. Proceedings of the IEEE Symposium on
Computational Intalligence in Security and Defense
Applications, pp. 53-58.
Weiss, G. M., Provost, F., 2003. Learning When Training
Data are Costly: The Effect of Class Distribution on
Tree Induction. Journal of Artificial Intelligence
Research 19, pp. 315-354.
Witten, I. H., Frank, E., 2011. Data Mining: Practical
Machine Learning Tools and Techniques. Morgan
Kaufmann, San Francisco, 3
rd
edition.
KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
352
