
Fuzzy Base Predictor Outputs as Conditional Selectors
for Evolved Combined Prediction System
Athanasios Tsakonas and Bogdan Gabrys
Smart Technology Research Centre, Bournemouth University, Talbot Campus, Fern Barrow, Poole, BH12 5BB, U.K.
Keywords:
Ensemble Systems, Fuzzy Rule-based Systems, Function Approximation, Genetic Programming.
Abstract:
In this paper, we attempt to incorporate trained base learners outputs as inputs to the antecedent parts in
fuzzy rule-based construction of hybrid ensembles. To accomplish this we adopt a versatile framework for the
production of ensemble systems that uses a grammar driven genetic programming to evolve combinations of
multilayer perceptrons and support vector machines. We evaluate the proposed architecture using three real-
world regression tasks and compare it with multi-level, hierarchical ensembles. The conducted preliminary
experiments showed very interesting results indicating that given a large pool of base predictors to choose
from, the outputs of some of them, when applied to fuzzy sets, can be used as selectors for building accurate
ensembles from other more accurate and complementary members of the same base predictor pool.
1 INTRODUCTION
The popularity of ensemble systems in real-world
tasks is a natural result of their effectiveness for a
range of tasks, where single predictors or classifiers
can overfit or provide weak solutions. A primary
property in ensemble systems, contributing to their
ability to generalize better is a combination of indi-
vidual performances and diversity among individual
learners (Brown et al., 2005). Recently, fuzzy ap-
proaches have been considered in order to combine
learners within the ensemble framework. The fuzzy
inference tries to model human perception when im-
precision is encountered. As a result, the model
often achieves equally good or better performance
while at the same time maintaining human readabil-
ity. There are many ways to incorporate fuzziness
into computational intelligence models including evo-
lutionary, neural and heuristic ones. The evolutionary
fuzzy models have some additional desirable prop-
erties, such as handling multi-objective constraints
(Ishibuchi, 2007), or implicit diversity promoting,
which is desirable in ensemble building (Brown et al.,
2005).
Various evolutionary training schemes have been
proposed, both at the learner level and at the combi-
nations. Evolutionary training of learners is demon-
strated in (Chandra and Yao, 2004), where neural net-
works are trained using evolutionary algorithms, fo-
cusing on maintaining diversityamong the learner po-
ol. Training by evolutionary means at the combiner
level is shown in the GRADIENT model (Tsakonas
and Gabrys, 2012) for generating multi-level, multi-
component ensembles, using grammar driven genetic
programming. GRADIENT incorporates, among oth-
ers, multilayer perceptrons and support vector ma-
chines, and its performance is successfully compared
with other state-of-the-art algorithms. The main ad-
vantage of the aforementioned model is the versatil-
ity provided by its architecture which incorporates a
context-free grammar for the description of complex
hierarchical ensemble structures. Multi-component,
hybrid ensemble systems are most commonly built
utilising independent training phases between the in-
dividual learners and their combinations. Building a
simple combination of trained learners does not re-
quire access to the training data for the combina-
tion to be performed as only outputs of the base pre-
dictors are required. When a fuzzy rule-based sys-
tem is trained, the rule antecedents make use of the
data attributes. Consequently, a fuzzy rule-based sys-
tem that combines learners is expected to make use
of the data attributes in its antecedents which would
lead to a divide and conquer strategy, as it was il-
lustrated in one of our previous papers (Kadlec and
Gabrys, 2011) or is quite common in some of the
local learning approaches to build global predictors.
However, there can be cases where for security or
other reasons, the data are not available at the com-
bination training phase, but only base predictor out-
34
Tsakonas A. and Gabrys B..
Fuzzy Base Predictor Outputs as Conditional Selectors for Evolved Combined Prediction System.
DOI: 10.5220/0004147600340041
In Proceedings of the 4th International Joint Conference on Computational Intelligence (ECTA-2012), pages 34-41
ISBN: 978-989-8565-33-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

puts from the whole pool are accessible. The idea of
this paper, is to investigate the effectiveness of a sys-
tem that produces a fuzzy model for combining learn-
ers, but which also restricts itself to knowledge about
the underlying problem. Such a model, named here-
inafter as PROFESS (PRedictor-Output Fuzzy Evolv-
ing SyStem) uses trained learners to feed the fuzzy an-
tecedents of the rules whose consequents are evolved
combined predictors. Based on GRADIENT’s versa-
tile framework, PROFESS extends the ensemble gen-
eration ability by providing a model for the creation
of fuzzy rule-based controlled ensembles, where the
fuzzy antecedent inputs are also the learners. To ac-
complish this, a new context-free grammar is intro-
duced which enables the creation of ensembles con-
sisted of fuzzy rules having learner combinations as a
consequent part, and learners in their antecedent part.
The paper is organized as follows. Next section
describes the background on related research. Sec-
tion 3 includes a detailed description of the system.
In section 4, we present our results from synthetic
and real-world data domains, and a discussion fol-
lows. Finally, section 5 includes our conclusions and
suggestions for further research.
2 BACKGROUND
Genetic programming (GP) is a successful branch of
evolutionary computing, with a number of desirable
properties (Koza, 1992). The main advantage of GP
resides in its ability to express arbitrarily large hi-
erarchical solutions representing functional equiva-
lents. Standard GP implementations derive simple
tree structures that describe programs or mathemati-
cal formulas. Later advances incorporated grammar
systems to GP enabling the production of more com-
plex solution forms, like Mamdani fuzzy rule based
systems (Alba et al., 1996), multilayer perceptrons
(Tsakonas, 2006) or Takagi-Sugeno-Kang fuzzy rule
based systems (Tsakonas and Gabrys, 2011).
Other enhancements on GP include splitting the
evolving population into semi-independent subpopu-
lations, in the so-called island models. These sub-
populations, also called demes, evolve independently
for a requested interval and periodically exchange a
number of individuals (Fernandez et al., 2003). The
improved diversity levels apparent to island models
made them attractive means for the implementation
of ensemble building systems. Such a model is pre-
sented in (Zhang and Bhattacharyya, 2004), where
GP is used to produce base classifiers which are then
combined by majority voting. A similar approach is
proposed in (Hong and Cho, 2006), however with the
learner combination taking into account the diversity
of the classifiers. In an advanced approach (Folino
et al., 2003), a cellular GP is used to combine deci-
sion trees for classification tasks.
Incorporating fuzziness into ensembles can take
the form of fuzzy application at base level, at com-
bination level, or both. At the combination level, a
fuzzy inference engine may be used for global se-
lection of base learners or for complete ensembles
(Duin, 2002). A comparison between fuzzy and non
fuzzy ensembles is presented in (Kuncheva, 2003),
where the authors design combinations of classifiers
using boosting techniques, in the AdaBoost environ-
ment. In that work, the fuzzy ensembles are shown
to achieve better performance in most of the tasks
addressed.Combining learners using fuzzy logic has
been applied in classification tasks in (Evangelista
et al., 2005). In that work, a fuzzy system aggre-
gates the output of support vector machines for binary
classification, in an attempt to reduce the dimension-
ality of the problems. The proposed model is tested
on an intrusion detection problem, and the authors
conclude that it is promising and it can be applied
to more domains. Another work (Jensen and Shen,
2009), presents three methods to apply selection in
an ensemble system by using fuzzy-rough features.
The suggested models are shown to produce ensem-
bles with less redundant learners. Other promising
methods to apply fusion using fuzziness include fuzzy
templates and several types of fuzzy integrals (Ruta
and Gabrys, 2000).
Although extended research has been accom-
plished for incorporating fuzziness into ensemble
building, most research deals with the application of
fuzziness to either base level, or to the combination
level for global selection of base learners (Sharkey
et al., 2000). Hence, few work has been done on fuzzy
rule based selection of ensembles, and the use of base
learner output for the antecedent part of such systems
has not been investigated yet. Still, the potential of
positive findings regarding the performance of an en-
semble system that creates combinations without ex-
plicit access to the original data - but only through its
learners - is significant. This work therefore, aims to
explore this configuration. Concluding the presenta-
tion of related background, we continue in the next
section by providing the system design details.
3 SYSTEM DESIGN
Following the principles of GRADIENT, three ba-
sic elements form the architecture of PROFESS
(Tsakonas and Gabrys, 2012):
FuzzyBasePredictorOutputsasConditionalSelectorsforEvolvedCombinedPredictionSystem
35

• Base learner pool. These learners are individually
trained at the beginning of the run.
• Grammar. The grammar is responsible for the
initial generation of combinations, and the subse-
quent control during evolution, for the production
of combined prediction systems.
• Combination pool. The combination pool is im-
plemented as the genetic programming population
and evolves guided by the grammar in the second
phase of training.
Training in PROFESS includes the following steps:
1. Creation of a learner pool.
2. Training of individual learners.
3. Creation of initial population of combined predic-
tors.
4. Evolution of combined predictors until termi-
nation criterion is satisfied (combined predictor
search).
Step 1 allocates resources for the generation of the re-
quested learner pool. In Step 2, the available learners
are trained, using standard training algorithms, such
as backpropagationfor neural networks. Step 3 gener-
ates the GP population, consisted of combined predic-
tion systems. One complete combined prediction sys-
tem represents one individual in the GP population.
The final step, Step 4, evolves the population until a
specific criterion is met. Considering the importance
of the grammar as a descriptor of PROFESS, we con-
tinue this section with a presentation of the adopted
grammar. We then describe the learner settings for
this work and this section concludes with a presenta-
tion of the evolutionary environment that is applied
during the combined predictors search phase.
3.1 Grammar
The proposed grammar aims to restrict the search
space and facilitate the generation of a fuzzy rule base
for the selection of ensembles. The fuzzy rules use
the output of base learners in the antecedent parts.
The fuzzy membership functions are further tuned by
evolutionary means, using two parameters: skew S
K
and slide S
L
. The first parameter (skew) extends or
shrinks the shape of the membership function, while
the second one (slide) shifts the center of the member-
ship function. The resulting function output z
A
k
, for a
Gaussian membership function A
k
is calculated using
Eq.1-3.
z
A
k
= e
x−c
A
k
w
A
k
2
(1)
N = { RL, RULE, IF, AND, THEN}
T = { LOW, MEDIUM, HIGH, ANN1, ANN2,..,ANNn,
SVM1, SVM2,..,SVMp }
P = {
<TREE> ::= <RL> | <RULE>
<RL> ::= RL <TREE><TREE>
<RULE> ::= RULE <COND><COMB>
<COND> ::= <IF > | <AND>
<IF > ::= IF <PRED><FSET><SLIDE><SKEW>
<AND> ::= AND <COND> <COND>
<FSET > ::= LOW | MEDIUM | HIGH
<COMB> ::= <FUNC><PRED><PRED> |
<FUNC><PRED><PRED><PRED> |
<FUNC><PRED><PRED><PRED><PRED>
<FUNC> ::= MEAN | MEDIAN | QUAD
<PRED> ::=ANN1 | ANN2 |..| ANNn |
SVM1 | SVM2 |..|SVMp
<SLIDE> ::=<NUMBER>
<SKEW> ::=<NUMBER>
<NUMBER> ::= Real value in [-L,L]
}
S = { RL }
Figure 1: Context-free grammar for PROFESS.
c
A
k
= c
mf
+ α
k
S
k
(2)
w
A
L
= w
mf
+ α
L
S
L
(3)
where c
mf
∈ {0, 0.5, 1}, w
mf
= 0.25, α
L
= 0.125,
α
K
= 0.2, with the last two parameters expressing the
preferred sensitivity of tuning, their selection depend-
ing on the expressiveness preference of the resulted
fuzzy rules. As base learners, multilayer perceptrons
and support vector machines are available. The rule
is in the following form:
R
i
: if F
m
is A
k1
[and F
p
is A
k2
...]
then y = E
i
with C (4)
i = 1, ..., m, C ∈ [0, 1]
where C is the certainty factor, F
m
,F
p
are selected
predictors, E
i
is a selected ensemble, and A
kn
are
fuzzy sets characterized by the membership functions
A
kn
(F
n
) . In this work, Gaussian membership func-
tions were applied. Three fuzzy sets per attribute were
available (Low, Medium, High). A grammar is de-
fined by the quadruple N, T, P, S where N is the set of
non-terminals, T is the set of terminals, P is the set of
production rules and S is a member of N that corre-
sponds to the starting symbol. The description of the
grammar for PROFESS is shown in Fig. 1.
3.2 Learners Setup
From the available learner and pre-processing library
of GRADIENT, for illustration purposes we selected
to include in PROFESS, multilayer perceptrons and
support vector machines. The multilayer perceptrons
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
36

Table 1: Learners configuration (T : transfer function in
hidden layers).
Parameter Value
MLP-NN #predictors 100
MLP-NN #hidden layers 2
MLP-NN sigmoid T prob. 0.5
MLP-NN stepwise sigmoid T prob. 0.1
MLP-NN gaussian T prob. 0.3
MLP-NN elliot T prob. 0.1
MLP-NN Iterations 3,000
SVM #predictors 100
SVM Max. Iterations 50,000
SVM RBF γ lowest 10
−5
SVM RBF γ highest 10
15
Predictors subset size 60%
Predictors subset domain Global
consist of two hidden layers. The number of neurons
in every hidden layer N
i,i=1,2
k
of a neural network K,
is randomly set according to Equation 5:
N
i
k
= (0.5+U(1))n
k
(5)
where U(1) returns uniformly a random number in
[0, 1] and n
k
is the positive root of Equation 6 for P
k
attributes (network inputs), T
k
training rows and l hid-
den layers (here l = 2).
n
k
= (l − 1)x
2
+ (1+ P
k
)x−
T
k
2
(6)
The transfer functions in hidden layers where also
randomly set, selecting among Sigmoidal, Gaussian
and Elliot functions. The resilient backpropagation
algorithm was preferred for training. We trained a
pool of 100 multilayer perceptrons. The support vec-
tor machines incorporated a radial basis function ker-
nel, and the γ parameter was randomly selected from
[10
−5
, 10
15
]. In the learner pool, 100 support vec-
tor machines were available. The training datasets
for learners consist of randomly sub-sampled sets of
the available training data sets (Tsakonas and Gabrys,
2012). Table 1 summarizes the learner settings.
3.3 Evolutionary Setup
After the training phase of learners is completed in
PROFESS, the next stage involves creation and train-
ing of the pool of combined predictors. Individuals
in the evolutionary population are created and trained
under the constraints of the defined grammar. Each
individual corresponds to one fuzzy rule base of en-
sembles. As combiners, the arithmetic mean and the
median were available. This training makes use of
a multi-population genetic programming framework.
Table 2: Evolutionary parameters.
Parameter Value / Value range
GP System Grammar-driven GP
Subpopulations 5
Subpopulation topology Ring
Isolation time 7 generations
Migrants number 7 individuals
Migrants type Elite individuals
Total population 150 individuals
Selection Tournament
Tournament size 7
Crossover rate 0.7
Mutation rate 0.3
Max.individual size 150/500 nodes
Max.generations 50
In this work, five subpopulations are used, a value
which is typical in multi-population models (Fernan-
dez et al., 2003). These subpopulations are trained for
a period of 7 generations, and they exchange 7 indi-
viduals, under a ring scheme of migration. This pro-
cess is repeated until 50 generations are completed.
As fitness function, the mean-square-error (MSE) is
used. A summary of the parameters for the evolution-
ary training of the combined predictors is shown in
Table 2.
3.4 Data
We compared PROFESS with regression models us-
ing a synthetic data problem, and with GRADIENT
using three real-world datasets, taken from the UCI
Machine Learning repository (Frank and Asuncion,
2010). The properties of the datasets are shown in Ta-
ble 3. We created three data permutations for every
real-world problem. In all cases, we used one third of
the data as a test set. The synthetic data task was the
Jacobs data (Jacobs, 1997) that involves five indepen-
dent attributes x
1
, ..., x
5
. All attributes are uniformly
distributed at random over [0, 1]. The function output
is calculated by Equation 7.
y =
1
13
(10sin(πx
1
x
2
) + 20
x
3
−
1
2
2
+10x
4
+ 5x
5
) − 1+ ε (7)
where ε is Gaussian random noise with σ
2
ε
= 0.2. We
generated a dataset consisting of 1,500 rows.
4 RESULTS AND DISCUSSION
We applied PROFESS to the available datasets, us-
ing the configuration shown in Tables 1 and 2. Ta-
FuzzyBasePredictorOutputsasConditionalSelectorsforEvolvedCombinedPredictionSystem
37

Figure 2: Evolved combined system for the Slump test problem.
Table 3: Datasets used.
Domain Instances Attributes
Jacobs 1500 5
Slump test 103 7
CPU Performance 209 6
Boston housing 506 13
ble 4 shows a comparison with WEKA (Hall et al.,
2009) regression methods for the synthetic data prob-
lem. The results of our experiments for real world
data, as compared to GRADIENT are shown in Table
5. In this table, the results are expressed in average
mean-square-error (MSE) with 0.95% confidence in-
tervals. As it can be seen in the table, PROFESS man-
aged to achieve lower average MSE than GRADIENT
in the problems addressed. As an example of output,
the evolved solution for the first permutation of the
Slump test problem is shown in Fig.2. This solution
is corresponding to the following rule base:
R
1
: if S006 is High(−0.06219, −0.22473) then
Median(S040, N063, N019, N092, S014, N032, N080)
R
2
: if N099 is Medium(−0.46393, −0.29883) then
Median(N032, N063, N087, S061, S060, S027, S087)
R
3
: if N099 is Medium(0.94855, −0.29883) then
Median(N070, S064, N087, N092, S060, S027, S087)
R
4
: if S035 is High(−0.06219, − 0.22473) then
Median(S040, N063, N087, N092, S060, S027, S028)
where the first variable in the fuzzy set corresponds
to the slide parameter of the membership function S
L
,
and the second is the skew parameter S
K
. The evolved
membership functions are shown in Fig.3. It is worth
noting, that the most common case observed was that
learners feeding the antecedent parts were not appear-
ing in the consequent part of any rule.
Tables 6, 7 and 8 compare the best obtained results
using the proposed system to results found in the lit-
erature.
• In Slump test data, we compared the results us-
ing the Pearson correlation coefficient for com-
patibility with the results reported in the literature.
In this case, the best model resulting from PRO-
FESS was not better than the other reported mod-
els, with the best model of GRADIENT having
the higher correlation coefficient.
• In CPU performance data, the Pearson correlation
coefficient for PROFESS was the highest among
the compared approaches.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
38

Table 4: Comparative results on Jacobs data.
Model RMSE
RBF network
1
.1659
Isotonic Regression
1
.1469
Pace Regression
1
.0966
SMO Regression
1,2
.0960
PROFESS (this work) .0958
1. (Hall et al., 2009).
2. (Scholkopf and Smola, 2002).
• In Boston housing data, the best model of PRO-
FESS had lower error than the reported literature
ones.
Table 5: Results in three real-world datasets. Values are av-
erage MSE from three permutations, with 0.95% confidence
intervals.
Domain GRADIENT PROFESS
Slump test 40.33 ± 19.23 39.83 ± 9.53
CPU 9575 ± 7789 9461 ± 6267
Boston housing 13.43 ± 1.04 10.68 ± 2.97
Table 9 compares the evolved size, measured in
the number of nodes, of the solutions. The implemen-
tation of a grammar for fuzzy systems requires a large
number of intermediate functions to allow the incor-
poration of a similar number of base learners. For this
reason, we have set in our experiments the maximum
possible solution size to 500 nodes for PROFESS,
while for GRADIENT a maximum of 150 nodes was
kept since it could express similarly sized (in terms of
learner participation) ensembles.
Although the maximum size was set high, PRO-
FESS managed to evolve comparable solutions, in
terms of size, to GRADIENT’s. This resulted in
producing rule bases with a small number of rules,
which we consider is a result of the expressiveness of
PROFESS’s grammar. The latter conclusion is more
clearly depicted in Table 10, where the average num-
ber of learner instances in a solution is shown. In this
table, it is clear that PROFESS required, on average,
a significantly smaller number of learner participation
to evolve competitive results. As expected, the val-
ues shown in Table 10 concern only the learner in-
stances that appear in combined predictors, and they
don’t take into account the occurrence of the learners
in the antecedent part of PROFESS’s rules.
Table 6: Slump test data comparison on unseen data. Re-
sults for PROFESS correspond to the Pearson correlation
coefficient of best model.
Model R
2
Neural network
1
.922
P2-TSK-GP (3 MF)
2
.9127
GRADIENT(NN-30/Mean)
3
.9694
PROFESS (this work) .8257
1. (Yeh, 2008).
2. (Tsakonas and Gabrys, 2011).
3. (Tsakonas and Gabrys, 2012).
Table 7: CPU performance data comparison on unseen data.
Results for PROFESS correspond to the Pearson correlation
coefficient of best model.
Model R
2
Original Attributes
M5
1
.921
M5 (no smoothing)
1
.908
M5 (no models)
1
.803
GRADIENT (NN-30/Median)
2
.970
PROFESS (this work) .978
Transformed Attributes
Ein-Dor
3
.966
M5
1
.956
M5 (no smoothing)
1
.957
M5 (no models)
1
.853
1. (Quinlan, 1992).
2. (Tsakonas and Gabrys, 2012).
3. (Ein-Dor and Feldmesser, 1984).
Figure 3: Evolved membership functions for Slump test
problem.
5 CONCLUSIONS AND FURTHER
RESEARCH DIRECTIONS
This work presented a system for the generation of
multi-component fuzzy rule-based ensembles using
FuzzyBasePredictorOutputsasConditionalSelectorsforEvolvedCombinedPredictionSystem
39
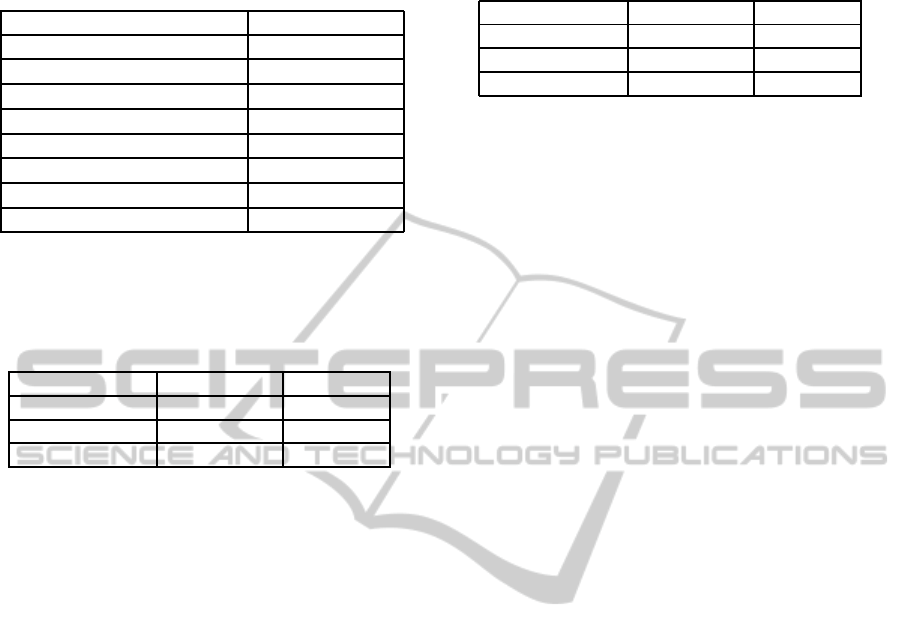
Table 8: Boston housing data comparison on unseen data.
Results for PROFESS correspond to the best model.
Model RMSE
GASEN
1
10.68
Random Forest
2
3.26
Fuzzy CART
3
3.40
Fuzzy CART + PLM
3
3.10
Fuzzy CART + Bagging
3
3.26
Fuzzy CART + Smearing
3
3.21
GRADIENT (NN-30/Mix)
4
2.66
PROFESS (this work) 2.639
1. (Zhou et al., 2001).
2. (Liaw and Wiener, 2002).
3. (Medina-Chico et al., 2001).
4. (Tsakonas and Gabrys, 2012).
Table 9: Average evolved solution size (in nodes).
Domain GRADIENT PROFESS
Slump test 106.1 181.5
CPU 101.6 165.9
Boston housing 72.6 75.0
base learners in the antecedent part of fuzzy rules.
To accomplish this, we have decided to modify the
grammar of a versatile environmentfor the production
of multi-level, multi-component ensembles, named
GRADIENT. The new proposed model, named PRO-
FESS, features a novel grammar that produces arbi-
trarily large fuzzy rule bases that enable the selection
of complete ensembles, using the output of base learn-
ers as criterion. This approach can facilitate the de-
velopment of combined predictors, in environments
were only access to the base learners is possible, and
any use of the original training dataset is restricted to
base learning level.
To examine the effectiveness of the proposed
model, we tested it on a synthetic data problem and
three real-world datasets. The results from our exper-
iments show that the model is able to provide com-
petitive performance as compared to the standard ap-
proach. This conclusion facilitates the definition of
environments were a set of trained learners may sub-
stitute the original data in tasks were the formation
of an ensemble is required. Applications of this ap-
proach can include situations where for security or
other reasons, the access to the original data is not
possible or highly restricted.
We consider that our initial findings presented in
this paper deserve further investigation. In the con-
ducted experiments we observed that, commonly, se-
lected learners in the antecedent part were not in-
cluded in consequent parts of the rules. We will there-
fore further investigate this case. It is clear that the
Table 10: Average evolved solution size (in learner in-
stances appearing in combinations).
Domain GRADIENT PROFESS
Slump test 67.6 40.4
CPU 35.2 22.6
Boston housing 71.6 54.8
complementary information resides in the whole pool
of base learners and while some of them are not ac-
curate enough to be used for prediction, they seem
to play and important role in the selection process of
ensembles consisting of a number of other predictors
from the pool. This finding is completely novel and
the analysis of the relationships between the ”selec-
tor” learners used in the antecedents of the fuzzy rules
and the ”combined predictors” which form the con-
sequent part of these rules is a fascinating subject to
follow. Finally, further tuning of the evolutionary pa-
rameters will take place, in an attempt to reduce the
required resources and increase the algorithmic effi-
ciency.
ACKNOWLEDGEMENTS
The research leading to these results has received
funding from the European Commission within the
Marie Curie Industry and Academia Partnerships and
Pathways (IAPP) programme under grant agreement
n. 251617.
REFERENCES
Alba, E., Cotta, C., and Troya, J. (1996). Evolutionary de-
sign of fuzzy logic controllers using strongly-typed
gp. In Proc. 1996 IEEE Int’l Symposium on Intelli-
gent Control. New York, NY.
Brown, G., Wyatt, J., Harris, R., and Yao, X. (2005). Di-
versity creation methods: a survey and categorisation.
Inf. Fusion, 6(1):5–20.
Chandra, A. and Yao, X. (2004). Divace: Diverse and accu-
rate ensemble learning algorithm. LNCS 3177, IDEAL
2004, 17(4):619–625.
Duin, R. (2002). The combining classifier: to train or not
to train? In Proc. of the 16th Int’l Conf. on Pattern
Recognition, pages 765–770.
Ein-Dor, P. and Feldmesser, J. (1984). Attributes of
the performance of central processing units: A rela-
tive performance prediction model. Commun. ACM,
30(30):308–317.
Evangelista, P., Bonissone, P., Embrechts, M., and Szyman-
ski, B. (2005). Unsupervised fuzzy ensembles and
their use in intrusion detection. In European Sym-
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
40

posium on Artificial Neural Networks (ESANN’05).
Bruges, Belgium.
Fernandez, F., Tommassini, M., and Vanneschi, L. (2003).
An empirical study of multipopulation genetic pro-
gramming. Genetic Programming and Evolvable Ma-
chines, 4(1).
Folino, G., Pizzuti, C., and Spezzano, G. (2003). Ensem-
ble techniques for parallel genetic programming based
classifiers. In C.Ryan, T.Soule, M.Keijzer, et al.(Eds.),
Proc. of the European Conf. Gen. Prog.(EuroGP 03),
LNCS 2610, pages 59–69. Springer.
Frank, A. and Asuncion, A. (2010). UCI Machine Learning
Repository [http://archive.ics.uci.edu/ml]. CA: Uni-
versity of California, School of Information and Com-
puter Science, Irvine.
Hall, M., Frank, E., Holmes, G., Pfahringer, B., Reutemann,
P., and Witten, I. (2009). The weka data mining soft-
ware: An update. SIGKDD Explorations, 11(1).
Hong, J. and Cho, S. (2006). The classification of cancer
based on dna microarray data that uses diverse en-
semble genetic programming. Artif. Intell. in Med.,
36(1):43–58.
Ishibuchi, H. (2007). Multiobjective genetic fuzzy systems:
Review and future research directions. In IEEE Int’l
Conf. on Fuzzy Systems (FUZZ-IEEE 2007), pages
59–69. Imperial College.
Jacobs, R. (1997). Bias-variance analyses of mixture-of-
experts architectures. Neural Computation, 0:369–
383.
Jensen, R. and Shen, Q. (2009). New approaches to fuzzy-
rough feature selection. IEEE Trans. on Fuzzy Sys-
tems, 17(4):824–838.
Kadlec, P. and Gabrys, B. (2011). Local learning-based
adaptive soft sensor for catalyst activation prediction.
AIChE Journal, 57(5):1288–1301.
Koza, J. (1992). Genetic programming - On the program-
ming of computers by means of natural selection. The
MIT Press, Cambridge, Massachussets, USA.
Kuncheva, L. (2003). Fuzzy versus nonfuzzy in combin-
ing classifiers designed by boosting. IEEE Trans. on
Fuzzy Systems, 11(6):729–741.
Liaw, A. and Wiener, M. (2002). Classification and regres-
sion by randomforest. Expert Systems with Applica-
tions (Under Review).
Medina-Chico, V., Suarez, A., and Lutsko, J. F. (2001).
Backpropagation in decision trees for regression. In
ECML 2001, LNAI 2167, pages 348–359, Springer
Verlag.
Quinlan, J. R. (1992). Learning with continuous classes. In
AI’92, Singapore: World Scientific.
Ruta, D. and Gabrys, B. (2000). An overview of classifier
fusion methods. Computing and Information Systems,
7(2):1–10.
Scholkopf, B. and Smola, A. (2002). Learning with Ker-
nels - Support Vector Machines, Regularization, Op-
timization and Beyond. The MIT Press, Cambridge,
Massachussets, USA.
Sharkey, A., Sharkey, N., Gerecke, U., and Chandroth, G.
(2000). The test and select approach to ensemble com-
bination. Multiple Classifier Systems, LNCS 1857,
pages 30–44.
Tsakonas, A. (2006). A comparison of classification accu-
racy of four genetic programming evolved intelligent
structures. Information Sciences, 17(1):691–724.
Tsakonas, A. and Gabrys, B. (2011). Evolving takagi-
sugeno-kang fuzzy systems using multi-population
grammar guided genetic programmings. In Int’l Conf.
Evol. Comp. Theory and Appl. (ECTA’11), Paris,
France.
Tsakonas, A. and Gabrys, B. (2012). Gradient:
Grammar-driven genetic programming framework
for building multi-component, hierarchical predic-
tive systems. Expert Systems with Applications,
DOI:10.1016/j.eswa.2012.05.076.
Yeh, I.-C. (2008). Modeling slump of concrete with fly
ash and superplasticizer. Computers and Concrete,
5(6):559–572.
Zhang, Y. and Bhattacharyya, S. (2004). Genetic pro-
gramming in classifying large-scale data: an ensemble
method. Information Sciences, 163(1):85–101.
Zhou, Z., Wu, J., Jiang, Y., and Chen, R. (2001). Genetic
algorithm based selective neural network ensemble.
In 17th Int’l Joint Conf. Artif. Intell., pages 797–802,
USA, Morgan Kaufmann.
FuzzyBasePredictorOutputsasConditionalSelectorsforEvolvedCombinedPredictionSystem
41
