
Alternative Analysis Networking
A Multi-characterization Algorithm
Kevin Albarado and Roy Hartfield
Department of Aerospace Engineering, Auburn University, Auburn, AL, U.S.A.
Keywords:
Particle Swarm, Neighborhooding, Unsupervised Training, Kohonen.
Abstract:
A neural network technique known as unsupervised training was coupled with conventional optimization
schemes to develop an optimization scheme which could characterize multiple “optimal” solutions. The tool
discussed in this study was developed specifically for the purposes of providing a designer with a method
for designing multiple answers to a problem for the purposes of alternative analysis. Discussion of the algo-
rithm is provided along with three example problems: unconstrained 2-dimensional mathematical problem, a
tension-compression spring optimization problem, and a solid rocket motor design problem. This algorithm
appears to be the first capable of performing the task of finding multiple optimal solutions as efficiently as
typical stochastic based optimizers.
1 INTRODUCTION
Numerous methods for optimizing constrained, com-
plex problems have been proposed and proven to be
successful in implementation (Holland, 1992; Eber-
hart and Kennedy, 1995). In 1975, John Holland
first suggested modeling optimization schemes af-
ter phenomena observed in nature such as evolution,
crossover, mutation, etc. which eventually developed
into what is now called a genetic algorithm. Eberhart
and Kennedy followed suit by developing the particle
swarm optimizer, which mimics behavior of crowd-
ing and flocking observed in birds, insects, and mam-
mals alike. Both of these concepts are population
based stochastic methods. On their own, population
based methods are very efficient at finding designs
near the global optimum, but can never be gauranteed
to find the absolute global minimum point. For that
reason, Jenkins and Hartfield (Jenkins and Hartfield,
2010) added a pattern search optimization routine to
the particle swarm routine to form a hybrid optimiza-
tion routine that can effectively move off of local op-
tima and still climb the hills to find the global optima.
This same setup has been implemented into a strat-
egy for finding multiple optimal solutions by using a
concept known as neighborhooding. Neighborhood-
ing traditionally is the limiting of information for a
which particle can access in the particle swarm opti-
mization technique. Typically, this information limi-
tation is random with no real structure or organization
(Eberhart and Kennedy, 1995). In this work it is
shown that by simply restricting the communication
topology amongst the particles, self-organized com-
munication networks can be formed, resulting in an
environment suitable for multi-characterization of lo-
cal optima. The restricting topology was formed us-
ing unsupervised training to classify the initial popu-
lation into individual clusters of particles (henceforth
called neighborhoods).
2 UNSUPERVISED TRAINING
Unsupervised Training was developed by the neural
network community as a method for classifying clus-
ters of data when no metric for classification was
available (Masters, 1993). The concept of compet-
itive learning and self organization was developed
by Tuevo Kohonen (Kohonen, 2001). Typical neural
network training updates all neuron weights through
each training iteration. For unsupervised training,
however, neurons compete for learning. The Koho-
nen network follows this same logic, however input
normalization occurs before training thereby creating
a three layer network. Kohonen training is a six step
exercise that is repeated iteratively until the network
converges to a steady state. These steps are:
1. Normalize input patterns such that inputs fall onto
an N-dimensional hypersphere where N is the
183
Albarado K. and Hartfield R..
Alternative Analysis Networking - A Multi-characterization Algorithm.
DOI: 10.5220/0004147901830188
In Proceedings of the 4th International Joint Conference on Computational Intelligence (ECTA-2012), pages 183-188
ISBN: 978-989-8565-33-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

number of inputs.
z
n
=
x
n
q
∑
N
i=1
x
2
i
(1)
where x is the initial set of inputs, and z are the
normalized inputs.
2. Randomly initialize weights, w, for the desired
number of neurons and normalize weights accord-
ing to Equation 2.
w
n
=
w
n
q
∑
N
i=1
w
2
i
(2)
3. One input pattern at a time, apply the inputs to
each neuron.
net =
N
∑
i=1
z
i
w
i
= ZW
T
(3)
4. Update neuron with the highest net value
W
k
= W
k
+ αZ (4)
where α is a learning constant
5. Renormalize new weights using Equation 2.
6. Repeat 3, 4, and 5 for each input pattern.
Two important properties of note for this classifica-
tion method are that during the training, some neu-
rons will never take part in learning, which will lead
to neighborhoods being unoccupied, and there is no
restriction on how large or small a neighborhood can
be. In a 2-dimensional sense, the Kohonen technique
divides the domain into unequally sized “slices of
pie”, and whichever slice of pie a particle falls within
dictates which neighborhood that particle belongs to.
This is demonstrated in Figure 1. From the Figure, it
is shown how seemingly unclustered data can be clus-
tered into distinct groups. These individual groups
will form neighborhoods of particles that will be ap-
plied to the optimization schemes to be discussed.
Having the ability to define the number of neighbor-
hoods desired effectively gives the user the freedom
to estimate the number of local optima to search for.
3 OPTIMIZATION
After setting up the neighborhoods, three distinct op-
timization phases take place: base level optimization
within the individual neighborhoods, a second level
optimization amongs the top performers from each
neighborhood, and a gradient based routine for solu-
tion refinement. This last point is directly inspired by
the successes demonstrated by (Jenkins and Hartfield,
2010).
3.1 Base Level Optimization
The particle swarm technique was used for base level
optimization. Particles were limited in communi-
cation to only the particles within a given neigh-
borhood. The equations of motion for a particle
were unchanged from those presented by Mishra
(Mishra, 2006) in the repulsive particle swarm opti-
mizer (RPSO).
v
i+1
= R
1
αω( ˆx
m
− x
i
) + R
2
β( ˆx
i
− x
i
)
+ ωv
i
+ R
3
γ (5)
x
i+1
= x
i
+ v
i+1
(6)
The Mishra RPSO algorithm was used due to its ro-
bustness as compared to the basic particle swarm op-
timizer. In particular, the Mishra algorithm is more
effective in especially complex design spaces, and has
been tested on a wide array of functions.
3.2 Second Level Optimization
The second level optimization was implemented so
that the neighborhoods could move throughout the
design space. Without a second level optimization
in place, each neighborhood would locate an opti-
mum within the local domain, but all collectively
could fail to find the optimal “region” in the entire
design space. The second level optimization pro-
vides a way for the neighborhoods to move as whole.
The method implemented in this study was an atomic
attraction/repulsion model. This model was cho-
sen somewhat arbitrarily but proved to be success-
ful. Future work would involve investigating other
models for this phase of optimization. The attrac-
tion/repulsion model is represented as
x
i+1
= − ( ˆx
m
− x
i
)
γ
( ˆx
m
− x
i
)
2
−
ω
( ˆx
m
− x
i
)
4
!
(7)
where ˆx
m
represents the global best member, and x
represents the positions of the neighborhood best par-
ticles. γ and ω are tuning parameters.
3.3 Gradient based Optimization
A gradient based minimization routine was added
to refine the best members of each neighborhood.
This improves the probability that true local optima
are found. The minimization scheme was the pat-
tern search method developed by Hooke and Jeeves
(Hooke and Jeeves, 1961). This method is robust
and does not require exact calculation of the gradient.
Rather, the pattern search method evaluates the gradi-
ent in each direction and performs a collective pattern
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
184
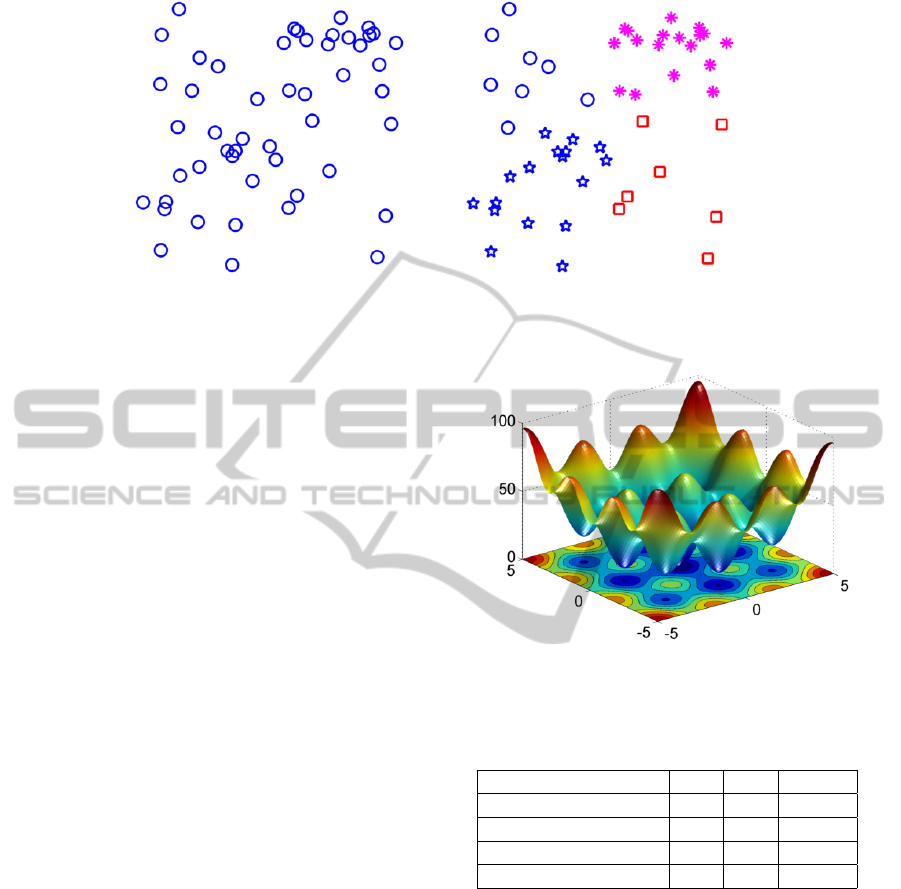
(a) Initial patterns. (b) Assigned patterns.
Figure 1: This Kohonen training example demonstrates 50 randomly distributed, unclustered particles separated into 4 distinct
groups.
move in the direction of steepest descent. The pat-
tern search method implemented into AAN based on
the results observed by Jenkins and Hartfield (Jenkins
and Hartfield, 2010). At the end of each base and sec-
ond level maneuver, a pattern search is performed on
the best performing members of each neighborhood.
4 RESULTS
Three test cases were performed with increasing com-
plexity. The first test case is a simple 2-dimensional
mathematical optimization problem that is uncon-
strained but fraught with numerous local optima. The
second test case is a constrained tension/compression
spring design problem with four input variables. The
final case is a rocket motor design problem which
presents numerous constraints, and is fraught with nu-
merous local and global optima.
4.1 Case 1: Unconstrained Math
Problem
The unconstrained math problem provides a valida-
tion that the optimization scheme works correctly.
The answer is known beforehand, and can be verified
quickly. In the case of classifying multiple optimal
solutions, the unconstrained math problem still needs
to be somewhat complex. Equation 8 results in the
surface shown in Figure 2 which is fraught with nu-
merous local minima and maxima.
z = 25
sin
2
x + sin
2
y
+ x
2
+ y
2
(8)
where x and y lie in the domain of [−5, 5]. The sur-
face has 8 local minima, 1 global minimum, 12 lo-
cal maxima, and 4 global maxima. The global min-
imum lies at the origin with the global maxima at
Figure 2: Surface/Contour for unconstrained problem z =
25(sin
2
x + sin
2
y) + x
2
+ y
2
.
Table 1: Global and local minima, locations and output val-
ues.
Minima Number X Y Output
Global Minima 0 0 0
Major Local Minima ± 3 0 9.5
Major Local Minima 0 ± 3 9.5
Minor Local Minima ± 3 ± 3 19
the corners of the domain. Table 1 gives a listing of
the global and local minima and their associated out-
put. These locations will serve as comparison mark-
ers for the optimization performance. The difference
between the major local optima and the minor local
optima is the associated function cost. The minor lo-
cal have a higher function cost than that of the ma-
jor local minima, making finding them less of a pri-
ority. The optimizer was tested with 150 members
in the population, with the desired number of optima
found to be 9. For every iteration of the optimizer,
the pattern search was performed twice on each of the
top members of the neigbhorhoods, with an inspec-
tion range of 5% of the domain in each direction. The
AlternativeAnalysisNetworking-AMulti-characterizationAlgorithm
185

Table 2: Final results for the unconstrained math problem.
Minima Found % Total Found %
2 Major 97% 5 93%
3 Major 77% 6 62%
2 Minor 62% 7 27%
3 Minor 19%
tuning parameters for the particle swarm were all set
to 0.3. The optimizer iteration limit was set to 25.
This run was repeated 100 times to gauge how well
the optimizer performs at identifying all local minima
near the global minimum. Table 2 gives the statistics
from the 100 runs. The global minimum was found
in every run. From Table 2, the minor local minima
were found less often than the major local minima.
This was expected because as the solution develops,
the major local minima draw particles at minor local
minima away due to their lower function cost. It was
expected that finding 3 of the 4 minor local minima
should not happen nearly as often as finding 3 out of
the 4 major local minima. The optimizer will always
favor local minima with a better function cost over
others because the second level optimization scheme
will draw the neighborhoods toward the global min-
imum. Also from Table 2, five minima were found
93% of the time. Although not listed, at least four
minima were found in every run, including the global
minima in every run. This example demonstrates the
optimizer’s ability to simultaneuosly seek out local
optima but also jump from minor local optima to ma-
jor local optima and global optima. Demonstrating
this ability is a major step forward from a conven-
tional optimizer, which is capable of either only find-
ing global optima or only finding local optima, toward
an optimizer that can do both, and in some cases si-
multaneously.
4.2 Case 2: Tension/Compression
Spring Design
The tension/compression spring design problem has
been optimized previously by Coello (Coello Coello,
2000) and Hu et al. (Hu et al., 2003). This problem
represents a highly constrained engineering design
problem for which the near optimal solution has been
reported already. There have been no reported local
optima to the problem. Mathematically, the spring
design problem is formalized as minimization of the
weight of a tension compression spring via Equation 9
f (X) = (N + 2) Dd
2
(9)
where D is the mean coil diameter, d is the wire diam-
eter, and N is the number of active coils. The spring
Table 3: Constrained tension/compression spring results.
Coello Hu et. al This paper
d .05148 .05146 .05000
D .35166 .35138 .34749
N 11.63 11.60 11.13
G(1) -.00333 6.84e-9 -.04163
G(2) -.07397 -.07390 -.00354
G(3) -4.026 -4.0431 -4.2216
G(4) -.7312 -.73143 -.73500
f (X) .01270 .01266 .01141
design is subject to the following constraints.
G(1) = 1 −
D
3
N
71785d
4
≤ 0
G(2) =
4D
2
− dD
12566(Dd
3
− d
4
)
+
1
5108d
2
≤ 0
G(3) = 1 −
140.45d
D
2
d
≤ 0
G(4) =
D + d
1.5
− 1 ≤ 0
Because no local optima exist for this problem, the
end goal for the optimizer should be to find the single
global optima which meets the constraints. The opti-
mizer was executed using 150 members with 150 gen-
erations with 4 neighorhoods. The final results given
by Coello and Hu et al. are presented along side the
results for this study in Table 3. The optimizer devel-
oped in this study was able to retain the ability to find
the global optimum (and as it turns out, a better an-
swer for this problem than previously reported) when
no local optima exist despite the highly constrained
design space, demonstrating the communication abil-
ity available between the neighborhoods.
4.3 Solid Rocket Motor Design Problem
The solid rocket motor design problem is associated
with a highly complex design space typical of what
would be observed in a real world engineering de-
sign scenario. The solid rocket motor program uses 9
geometric variables to describe a solid rocket motor.
The specific geometric inputs used for this study are
described in full detail in (Ricciardi, 1992; Hartfield
et al., 2004). The goal for the optimizer in this case
study was to find as many motor geometries that pro-
duces 300 psi pressure for 20 seconds exactly as pos-
sible. The performance metric for this problem is the
RMS error between the output pressure-time profile
and the neutral 300 psi-20 second curve desired. This
is a common solid rocket motor problem but presents
a number of challenges. There are a total of nine inde-
pendent variables, making the design space complex
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
186

(a) Motor 1. (b) Motor 2.
(c) Motor 3. (d) Motor 4.
Figure 3: Pressure-time profile for four distinct solutions from solid rocket motor optimization.
Figure 4: Motor geometries 1-4 based on 9 independent variables.
AlternativeAnalysisNetworking-AMulti-characterizationAlgorithm
187

and difficult to visualize. Two of the independent pa-
rameters are integers. The first integer parameter, the
number of star points, has a large effect on the pro-
file of the pressure versus time curve (progressive, re-
gressive, neutral, etc.). The second integer parame-
ter, propellant selection is a series of choices and has
no meaningful gradient, as some propellant choices
are similar and some are very different. There are
numerous geometric constraints, some of which can
be handled implicitly by nondimensionalizing some
of the independent variables in an intelligent manner.
The optimizer was executed with 100 particles for 50
generations with 6 neighborhoods. The results of the
optimization were 4 unique solutions, shown in Fig-
ures 3 and 4. While the pressure-time curves were
not perfect, it is important to remember that the op-
timizer is looking for global and local optima. The
results in Figure 3 should be considered local optima,
as they are close (10% RMS) but not exact. From Fig-
ure 4, clearly the optimizer was searching vastly dif-
ferent areas of the design space. While the fuel type
selection was the same for all four, and the number of
star points for each motor was between 7 and 9, the
lengths of each motor are drastically different. This
example effectively demonstrates the full capabilities
of the optimizer at locating unique local optima in a
complex and constrained design space.
5 CONCLUSIONS
The development of population based optimization
routines brought about the capability to locate so-
lutions in a complex and constrained design space.
These stochastic schemes typically only develop a
single solution, usually the global optimum. In most
instances, however, it is desirable to find multiple op-
timal solutions. The algorithm described in this paper
is capable of accomplishing this feat. It was shown
in this study that the algorithm developed has the fol-
lowing advantages:
• From the unconstrained mathematical problem, it
was shown that the algorithm is capable of jump-
ing from minor local optima toward major local
optima and the global optima. This fact is impor-
tant in verifying that the optimizer will not simply
find a local optima within a local neighborhood
domain, but instead will make some attempt to
improve.
• The constrained tension/compression spring ex-
ample demonstrated the algorithm’s ability to nav-
igate a complex design space and constraints as
well as the algorithm’s ability to find a global op-
tima when no local optima are known to exist.
• The solid rocket motor example proved that the
algorithm can be effective in practical real world
engineering design problems.
• The Kohonen unsupervised training technique
provides the user the ability to define the number
of desired optimal solutions to search for.
While the development thus far shows great promise,
some improvements can still be made to make the al-
gorithm more efficient. A study of optimization tech-
niques should be performed for the base level and
second level optimization phases to determine which
combination of optimization schemes are most effi-
cient for a wide range of problems. The gradient
based scheme can also be improved by switching to
a more robust and efficient hill climbing routine.
REFERENCES
Coello Coello, C. (2000). Use of self-adaptive penalty ap-
proach for engineering optimization problems. Com-
puters in Industry, 41(2):113–127.
Eberhart, R. and Kennedy, J. (1995). A new optimizer using
particle swarm theory. Proceedings Sixth Symposium
on Micro Machine Human Science.
Hartfield, R., Jenkins, R., Burkhalter, J., and Foster, W.
(2004). A review of analytical methods for predicting
grain regression in tactical solid rocket motors. AIAA
Journal of Spacecraft and Rockets, 41(4).
Holland, J. (1992). Adaptation in Natural and Artificial Sys-
tems. MIT Press.
Hooke, R. and Jeeves, T. (1961). Direct search solution of
numerical and statistical problems. Journal of Associ-
ation of Computing Machinery, 8(2).
Hu, X., Eberhart, R., and Shi, Y. (2003). Engineering opti-
mization with particle swarm. Technical report, IEEE
Swarm Intelligence Symposium.
Jenkins, R. and Hartfield, R. (2010). Hybrid particle swarm-
pattern search optimizer for aerospace applications.
Technical report, AIAA Paper 2010-7078.
Kohonen, T. (2001). Self-Organizing Maps. Springer.
Masters, T. (1993). Practical Neural Network Recipes in
C++. Academic Press.
Mishra, S. (2006). Repulsive particle swarm method on
some difficult test problems of global optimization.
Technical report, Munich Persona RePEc Archive Pa-
per No. 1742.
Ricciardi, A. (1992). Generalized geometric analysis of
right circular cylindrical star perforated and tapered
grains. AIAA Journal of Propulsion and Power, 8(1).
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
188
