Similarity of Membership Functions

A Shaped based Approach

Ana Tapia-Rosero

1,2

, Antoon Bronselaer

and Guy De Tr

FIEC, Escuela Superior Polit

ecnica del Litoral, Campus Gustavo Galindo V, Guayaquil, Ecuador

Department of Telecommunications and Information Processing, Ghent University, Ghent, Belgium

Keywords:

Membership Function, Similarity, Cluster, Fusion, Decision-making.

Abstract:

In this paper, we propose a method to group similar membership functions, each of them representing the

opinion of an expert, to obtain a resulting membership function that represents alike opinions among a group.

The similarity is based on the shape characteristics of membership functions used to represent the expert

opinions on a speciﬁc criterion. There are several applications for the proposed method which include group

decision making, suitability analysis and consensual processes. In each of these applications diverse points of

view are present. The goals of the method are to detect similar membership functions, to establish a manner

that allows the selection of representative opinions and to obtain a result membership function that represents

a speciﬁc trend or a suitable concept for a group of similar membership functions. Our approach is based on

soft computing techniques, considering expert preferences as a matter of degree, including a novel method to

process similar opinions with more ease.

1 INTRODUCTION

A decision-making problem could be solved involv-

ing several experts, each of them, with a different

perspective of the problem (technical, economic, ad-

ministrative, etc.). When there are several people in-

volved it is desired to build a consensus; but some-

times if most of the experts follow a different trend

on the criteria (optimistic, risky, etc.), this is a hard

task to pursue. However, it is possible to suggest a

solution based on the fusion of similar opinions that

follow for a speciﬁc trend or which represent a suit-

able concept.

Nowadays, using soft computing techniques, a

person could express his/her expertise or preferences

through membership functions setting his/her level of

agreement over a speciﬁc criterion. It is not neces-

sary that all of the experts have preknowledge on soft

computing techniques to represent their preferences

P(x) as a matter of degree (i.e., 0 ≤ P(x) ≤ 1, where 0

denotes a complete disagreement on the criteria and 1

denotes the highest level of agreement) as long as they

provide some values (Dujmovi

c and De Tr

e, 2011)

that will be used for deﬁning the attribute criterion in

a membership function.

For example, consider that a company has to de-

cide if a product will stay in the market or not based

on its “acceptable level of sales” (criterion). One

strategy to solve this decision-making problem is that

each expert uses a membership function to express

what he or she understands to be an acceptable sales

level. Nevertheless, we will have a number of mem-

bership functions that equals the number of experts

involved. If there is a large number of experts the de-

cision maker could be overwhelmed with all of their

opinions, and taking a ﬁnal decision will become a

complex task. But, if there are some experts with sim-

ilar opinions (each opinion represented by a member-

ship function) in the group, it is possible to build clus-

ters considering the similarity of membership func-

tions in order to allow the decision maker to decide

among a reduced amount of opinions (Figure 1).

Among different experts, using membership

functions to represent the level of agreement over a

speciﬁc criterion, three scenarios might be possible:

1) all the experts have a similar opinion and hence

give a similar representation; 2) they all give a dis-

similar representation; or 3) there are several groups

of experts with similar representations. Considering

that all the experts contribute to some extent to the

ﬁnal decision, all these scenarios deserve to be ana-

lyzed. However, this paper will focus only on the third

scenario reﬂecting the preferences of expert groups

with similar membership functions. Notice that the

402

Tapia-Rosero A., Bronselaer A. and De Tré G..

Similarity of Membership Functions - A Shaped based Approach.

DOI: 10.5220/0004148204020409

In Proceedings of the 4th International Joint Conference on Computational Intelligence (FCTA-2012), pages 402-409

ISBN: 978-989-8565-33-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

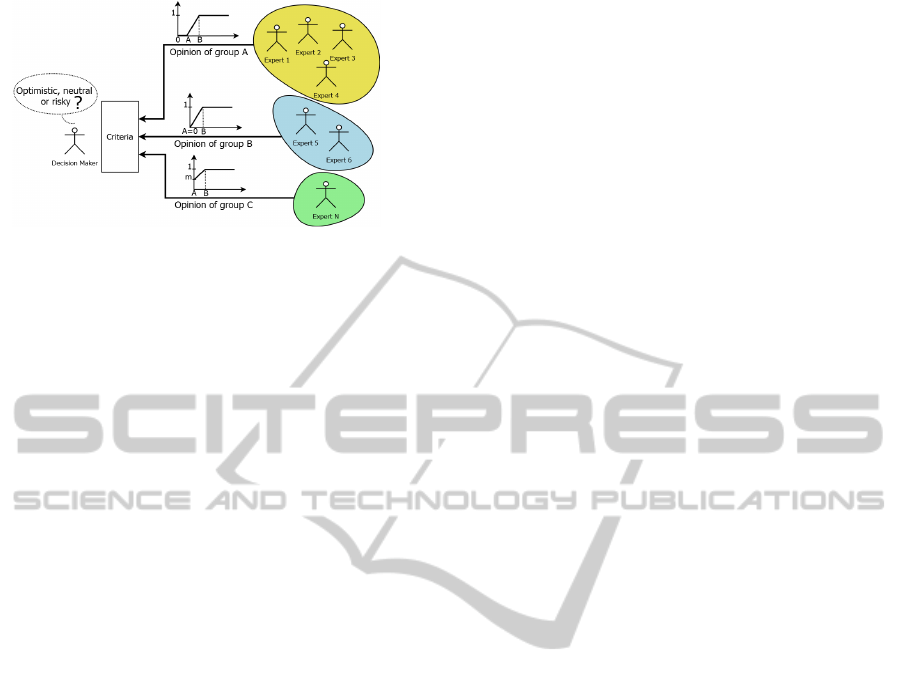
Figure 1: Representation of the opinions of multiple experts

grouped by similar membership functions.

remaining scenarios correspond to special cases of the

selected one.

A relevant question within the selected scenario

is: What happens if there exists a minority group

with a similar opinion (evaluation of the criteria) and

these experts are the most reliable among the others?

Should their opinions be considered or not? It is pos-

sible that this minority has relevant information that

should be considered related to the criteria or maybe

this minority is correct about some facts that may af-

fect the preference level.

There are several approaches to solve similar

decision-making problems. Some of them are focused

on the optimistic and the pessimistic points of view

(Rodr

ıguez et al., 2012) while others quantify the

number of experts that follow a trend (e.g., majority)

(Kacprzyk et al., 1992). Aditionally, there are various

similarity measures to compare fuzzy sets character-

ized by membership functions. This paper aims to

propose a method to group similar membership func-

tions using a shape based approach. This method al-

lows the decision-maker to select the group of opin-

ions that best suits the trend or concept of his/her

choice in order to obtain a resulting membership func-

tion that represent alike opinions among a group.

The proposed method uses a sequence of charac-

ters selected from a ﬁnite set of symbols {0, +, 1,

−, L, I, H} to annotate each membership function

considering slopes and different levels of agreement.

Within this paper, the term cluster will be used to rep-

resent a group of membership functions that have a

common shape characterized by the same character

string. As a result of the method a reduced amount

of opinions, each of them represented by a mem-

bership function, will be obtained. Several strate-

gies to fuse the membership functions, in a selected

group, could be considered; but, for illustrative pur-

poses only two basic operations are detailed within

this paper. Within the scope of this paper we will as-

sume that the decision-maker must select the cluster

of his/her preference to be analyzed taking into ac-

count that some sets of opinions could be, in some

extent, more representative than others.

The goals of the proposed method are: 1) to detect

similar membership functions, 2) to establish a man-

ner that allows the selection of representative opin-

ions and 3) to obtain a resulting membership function

that represents a speciﬁc trend or a suitable concept

of a group. This proposal is based on soft computing

techniques including the novelty of using a sequence

of characters to annotate and process similar opinions

represented by membership functions with ease.

The remainder of this paper is structured as fol-

lows. The second section includes some preliminary

concepts and related work. Section 3 provides details

on the main approach of this paper. Section 4 explains

the developed experiment. Section 5 concludes the

paper and proposes topics for further investigation.

2 PRELIMINARIES

A fuzzy set is a concept, fruitfully extended, from the

basic mathematical concept of a set (Zadeh, 1965).

According to Zadeh, a fuzzy set A on a universe X is

characterized by a membership function f

which as-

sociates each point x in X with a real number f

(x) in

the unit interval [0, 1 ] to represent its grade of mem-

bership in A. Values that are closer to the unit de-

note higher degrees of membership. Using a graph-

ical representation of the membership functions we

could identify different shape functions including the

trapezoidal membership function.

Trapezoidal membership functions, widely known

and frequently used for representing linguistic terms

(Klir and Yuan, 1995), have been selected in this pa-

per to represent the level of agreement of each expert

on the criteria. This selection has two main advan-

tages: 1) they could be built with only a few input val-

ues and 2) the deﬁnition of trapezoidal shaped func-

tions includes ﬁve intervals establishing a ﬁxed form

to represent different kinds of trapeziums.

The values used to build trapezoidal membership

functions are represented by letters (a, b, c, d) and the

relation among these values is that a≤b≤c≤d. Cases

like triangular membership functions are treated as a

special case of trapezium where b=c.

2.1 Fuzzy Similarity

This paper establishes, as a starting point, that two

membership functions are considered to be similar if

they have a similar shape. In order to detect similar

membership functions with ease, we use a sequence

of characters to represent the shape of a membership

SimilarityofMembershipFunctions-AShapedbasedApproach

403

function. One remark within this respect is that the

symbolic annotation must be done in such a way that

membership functions symbolized with the same se-

quence of characters must represent the same trend or

concept as expressed by the expert.

There are several ways to compare fuzzy sets and,

nowadays, various similarity measures have been dis-

cussed (Zwick and Carlstein, 1987; Le Capitaine,

2012). It is well known that most of the similarity

measures are either based on similarity relations, dis-

tance among fuzzy sets or set-theoretic operations.

2.1.1 Similarity Relations

The similarity relation deﬁnition was introduced by

(Zadeh, 1971) as an extension of the equivalence re-

lation concept for crisp sets. The deﬁnition states that

a similarity relation S on a universe X is a fuzzy rela-

tion that holds the following properties for all x, y, z

∈ X:

S(x,x) = 1 Reﬂexivity

S(x,y) = S(y,x) Symmetry

S(x,y) ∧ S(y, z) ≤ S(x, z) Transitivity

These properties have been considered in several

studies and we will recall the fuzzy similarity measure

for fuzzy sets deﬁned by Le Capitaine (2012):

A mapping S: F(X) x F(X) → [0, 1 ], with F(X)

denoting the powerset of all fuzzy sets that can be de-

ﬁned on X, is called a similarity measure if it satisﬁes:

P1. S(A,B) = S(B,A)

P2. S(A,A) = 1

P3. S(A,A

) = 0, A

denotes the complement of A

P4. A ⊆ B ⊆ C ⇒ S(A,C) ≤ S(A, B) ∧ S(B,C)

2.1.2 Distance among Fuzzy Sets

We found extensive literature (Xuecheng, 1992; Lee-

Kwang et al., 1994; Johany

ak and Kov

acs, 2005)

deﬁning different measures for the distance d(x, y)

between objects x and y based on known metrics

(e.g., Hausdorff, Hamming and Euclidean distances).

The notion of a distance between fuzzy sets has been

used as a measure of similarity, although some of

these similarity measures are considered theoretical

approaches because they suppose the existence of an

“ideal” fuzzy set (Merig

o and Casanovas, 2010). On

the other hand, most of the decision-making problems

do not have a given “ideal” solution considering that

we are looking for a resulting fuzzy set that better rep-

resents a trend or a concept in a given context.

To the best of our knowledge none of the dis-

tance based proposals make a distinction related to

the shape of the membership functions.

2.1.3 Set-theoretic Operations

This paper recalls the basic deﬁnitions of the

union and intersection operations proposed by Zadeh

(1965), considering two fuzzy sets A, B with respec-

tive membership functions f

and f

deﬁned on the

same universe X:

A∪B

(x) = max[f

(x), f

(x)], ∀x ∈ X (1)

A∩B

(x) = min[f

(x), f

(x)], ∀x ∈ X (2)

We must regard that other deﬁnitions based on tri-

angular norms and triangular conorms can be used

(e.g., the product and the probabilistic sum, the

Lukasiewicz t-norm and t-conorm, among others) to

combine the membership functions among a group.

There are several similarity measures based on

set-theoretic operations including Tversky (1977),

Dice (1945) and Jaccard indexes (1908). Within the

scope of this proposal, the main disadvantage on these

set-theoretic operations is that loss of information is

possible. Besides, it is feasible to consider that the

resulting membership functions could also include a

degree of conﬁdence to represent to what extent the

decision maker agrees on the resulting membership

function.

3 SIMILAR MEMBERSHIP

FUNCTIONS

This proposal is based on detecting similar member-

ship functions by comparing character strings. The

aforementioned string is easily built and it corre-

sponds to a sequence of characters that represents

the shape of a normalized membership function. Af-

ter the membership functions are clustered based on

their similarity this method incorporates two addi-

tional steps: 1) to choose a group of membership

functions that best suits the trend or concept accord-

ing to the selection of the decision-maker, and 2) to

select a strategy for fusion of the membership func-

tions that belong to the selected group.

3.1 String Representation for

Membership Functions

Bearing in mind that trapezoidal membership func-

tions have been selected, we could identify, graphi-

cally, the presence of segments in a trapezium shape.

These segments are based on the intervals of the trape-

zoidal membership function deﬁnition and all of them

belong to one of the following categories: positive

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

404

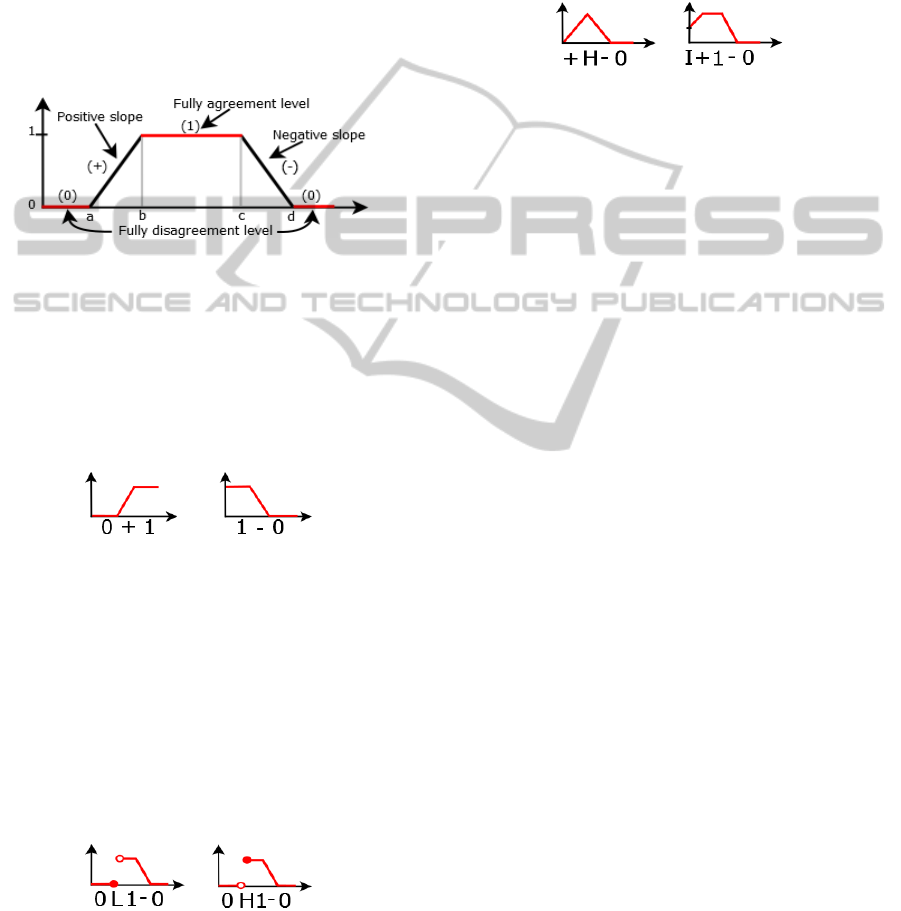
slope, negative slope, fully disagreement level, fully

agreement level, or point.

Each segment of the trapezium will use a symbol

among a sign {+, −} to represent the slope, a value

{0, 1} to represent the level of agreement (on seg-

ments without a slope) and a letter {L, I, H} to de-

note a point. The string representation of the mem-

bership function is built concatenating the character

that represents each segment considering the order in

the x-axis. Each character must correspond to a sin-

gle category. Figure 2, illustrates a trapezium and its

corresponding categories.

Figure 2: Segments of a trapezium and its categories.

The string representation of the presented trapez-

ium is “0+1−0” where each character of the string

corresponds to each segment of its function deﬁnition.

A feature that is noticeable graphically in some

trapezoidal membership functions is the absence of

segments on their shape. This case could be annotated

likewise resulting in shorter strings (Figure 3).

Figure 3: Examples of short string representations for mem-

bership functions.

The point category has a special use to depict a

speciﬁc value (on the x-axis) of non continuous func-

tions. In this case, we must represent this special

point with a letter corresponding to its level of agree-

ment. For simplicity, the letter is selected according

to the (high, intermediate or low) value of member-

ship at the mentioned point. Notice that the member-

ship functions of Figure 4, without the point category,

would be represented by the same string.

Figure 4: Examples of the string representations using the

point category in non continuous functions.

A triangular membership function is a special case

where b=c that is also annotated using a point cate-

gory. In this case we must represent the b=c point

at the highest (H) level of agreement for normalized

membership functions. In addition, the point cat-

egory allows representing different kinds of mem-

bership functions including those that have segments

with extreme values (start or end of the segment) at

intermediate levels of agreement. These membership

functions require representing the intermediate point

with the corresponding letter (Figure 5).

Figure 5: Examples of the string representation using the

point category at high and intermediate level of agreement.

The proposed string could represent different

kinds of membership functions using characters as de-

scribed before. Nevertheless, this method might be

extended in order to include other characteristics of

shapes (e.g., small core or long support based on a

threshold). Other adjustments could allow represent-

ing periodical functions and other special cases not

considered within the scope of this paper.

3.2 Similarity Measure

Within the scope of this paper, the similarity of mem-

bership functions is based on their shape characteris-

tics disregarding aspects as linear shifting. The shape

characteristics include the presence of slopes and lev-

els of agreement, components that are present in the

string representation detailed in Section 3.1.

To detect if two membership functions are similar

we need to accomplish the properties mentioned in

Section 2.1.1. This paper will use a straightforward

similarity measure based on the string representation

of the membership functions as follows:

S(A, B) =



0 , StrA 6= StrB

1 , StrA = StrB

(3)

where StrA and StrB are the string representations of

the corresponding membership functions.

The selected similarity measure will give us a

value, where 0 denotes no similarity and 1 denotes full

similarity among two fuzzy sets based on the shape of

their membership functions. Notice that the proposed

similarity measure allowed us to achieve the reﬂexiv-

ity, symmetry and transitivity properties.

3.3 Grouping Similar Membership

Functions

This proposal aims to build groups of membership

functions that represent a trend or concept in a

SimilarityofMembershipFunctions-AShapedbasedApproach

405

decision-making environment. Considering that sev-

eral experts might be involved and each expert could

suggest a membership function that represents his/her

level of agreement over a speciﬁc criterion, we should

group those membership functions that are consid-

ered similar. According to the similarity measure in

(3), two membership functions are considered simi-

lar if they have the same string representation. Within

this paper, the term cluster will be used to represent

a group of membership functions that have a com-

mon shape characterized by the same string; and it

is possible to obtain a cluster that contains a single

membership function. An important remark is that

membership functions that belong to the same cluster

or group accomplished the commutative, distributive

and associative properties to be considered similar.

3.4 Cluster Proﬁle

Considering that all experts contribute to some ex-

tent to the ﬁnal decision then all clusters deserve to

be analyzed; Furthermore, if we compare the number

of membership functions, that belongs to each clus-

ter, we could evaluate if a speciﬁc cluster represents

a majority, a minority or the same number of opin-

ions expressed by the membership functions present

in other clusters. It is achievable that some problems

could have a solution based on this number, but if we

return to the introductory questions it is possible that

other characteristics of the cluster must be taken into

account (e.g., the reliability of experts). It is possi-

ble that trying to represent the expert reliability might

become a subjective task. However, it is also possi-

ble that this reliability could be built based on some

characteristics that reﬂect the expert experience (e.g.,

number of hits on historic representations within the

same context).

3.5 Fusion of Similar Membership

Functions

When several membership functions are present to

represent a single trend or concept it is necessary to

select a strategy to obtain, as a result, the most repre-

sentative membership function. If we consider apply-

ing the set-theoretic operations to the following alter-

natives: a)the complete set of available membership

functions; b)a reduced set of membership functions

grouped by shape-similarity; then remarkable differ-

ences in the results are expected. For illustrative pur-

poses, this paper includes the results of applying the

union and intersection functions to both alternatives.

4 DEVELOPED EXPERIMENT

Considering that membership functions could be built

with some values to deﬁne the attribute criterion (Du-

jmovi

c and De Tr

e, 2011) and that several member-

ship functions were required to pursue the goals of

this paper an experiment was developed. A small

form was sent to different groups of people to col-

lect the values that will represent the agreement (of

each person) on a speciﬁc criterion. The groups were

not uniform considering different levels of knowledge

(students and profesionals), areas of expertise (engi-

neering, medicine and journalism) and personal pro-

ﬁles (single, married, parents, etc.). All the partici-

pants were adults (age≥18) with knowledge of ver-

balized terms that represent people’s age. The form

asked the participants, to suggest the range of ages

that they considered representative for different terms

like “baby”, “child” and “toddler”.

Two main cases were distinguished: 1) Some par-

ticipants expressed their preference among small val-

ues trying to represent that the term “baby” is suitable

since a boy or a girl was born until a certain age, and

2) other participants expressed their preference using

a range of values for fully agreement and fully dis-

agreement to represent the term “baby” (i.e., they use

the term “new born” for a small period).

4.1 Building the Membership Functions

A total of 74 membership functions were built using

the (a, b, c, d) values. Among participants who pre-

ferred small values, as shown in Figure 6, we distin-

guished cases where c6=d and others where c=d. The

last case depicts a non continuous function where c

represents fully agreement and values greater than d

represent fully disagreement.

Figure 6: Membership functions for preferred small values.

Among participants who preferred ranges of val-

ues we found cases where c<d and cases where c=d.

The last case represents a non continuous membership

function (Figure 7).

Figure 7: Membership functions for preferred range of val-

ues.

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

406

4.2 Detection of Similarity

The similarity is based on the shape characteristics

(slope, levels of agreement and continuity) of the

available membership functions represented by a se-

quence of characters. When the string representation

of each membership function is obtained, the similar-

ity detection based on the similarity measure stated in

(3) is performed. Equation 3 is the basis of a string

comparison where the same string represents a sim-

ilar shape. Table 1, shows the number of member-

ship functions on each group (represented by a string).

Note that two of these groups have a high number of

membership functions, which is consistent, because

“graphs of membership functions (elicited from dif-

ferent subjects) tend to have the same shape” (Klir

and Yuan, 1995).

Table 1: String representations and their corresponding fre-

quency.

String Representation Frequency

+1−0 1

+1H0 1

1−0 34

1H0 33

L1−0 1

L1H0 4

4.2.1 Selection of a Representative Opinion

To establish a manner that allows the selection of rep-

resentative opinions we prefer taking into account the

characteristics mentioned in Section 3.4. However,

within the scope of this paper we will assume that the

decision-maker will select the cluster of opinions that

best suits the trend or concept of his/her choice to be

analyzed.

In our case, we selected a cluster that represents

our preference expressed by a trapezoidal member-

ship function using small values. This selection tries

to represent that the term “baby” is suitable to rep-

resent the period starting when a boy or a girl was

born until a certain age. Our selection during the per-

formed experiment is the group represented by the

string “1−0” and we will refer to it as cluster A. Clus-

ter A corresponds to a majority, containing 34 trape-

zoidal membership functions. We will consider that

cluster A has a high reliability taking into account that

our participants have knowledge of verbalized terms

that represent ages including the term “baby”.

4.3 Fusion of Membership Functions

The union and intersection operations on fuzzy sets

were selected as basic operations to illustrate the

shape-similarity of membership functions. These set-

theoretic operations were executed over cluster A and

the entire group of membership functions. From now

on, we will refer to the entire group of membership

functions as group E.

The union and intersection operations use equa-

tions (1) and (2) respectively ∀x ∈ [0, n] where n is

greater than all the values d given by the participants.

The purpose of applying these operations is to ob-

tain as a result a reduced amount of opinions rep-

resented by a fuzzy set. For example, the group E

that contains 74 membership functions could be rep-

resented by the result of the union or the intersection

operation shown in Figure 8.

Figure 8: Result membership functions of Group E.

In an analogous form, the cluster A that con-

tains 34 similar-shaped membership functions could

be represented by the union operation or the intersec-

tion of its membership functions. Figure 9 shows the

result membership functions of these operations.

Figure 9: Result membership functions of Cluster A.

As expected, we obtain some differences between

the union and intersection operations over the com-

plete set of membership functions (Group E) and a re-

duced set of membership functions grouped by shape-

similarity (Cluster A). Graphically we could observe

that using the fusion of the membership functions of

SimilarityofMembershipFunctions-AShapedbasedApproach

407

a selected cluster will give us better results than se-

lecting the fusion of the entire group of membership

functions. This is conﬁrmed by calculating the mem-

bership function over the set-theoretic operations on

group E and cluster A. It is seen that the membership

grades in group E for small values (x≤10) are lower

than the membership grades in cluster A for the same

values.

For validation purposes, other clusters were ana-

lyzed and we obtained similar results but they are not

shown here due to space limits. Based on set-theoretic

operations, several membership functions were fu-

sioned to obtain a result membership function that

represents a trend or a suitable concept among several

opinions. Although, we have presented our results us-

ing the basic operations proposed by Zadeh, we have

evaluated our proposal with: 1) the Lukasiewicz t-

norm and t-conorm; and 2) the product and the proba-

bilistic sum. However, we obtained slightly different

results only for the t-norm over group E. More ad-

vanced fusion techniques are possible and subject to

further study. Here the use of union and intersection

operations are used to demonstrate the shape-based

similarity of membership functions.

5 CONCLUSIONS AND FURTHER

WORK

This paper proposed a novel method to annotate mem-

bership functions and build a string representation for

them. This string is used to detect similar-shaped

membership functions by string comparisons.

Similar membership functions were clustered con-

sidering that they represent a trend or a suitable con-

cept in a decision-making context. We proposed some

cluster characteristics to be taken into account for fur-

ther analysis. Additionally, for any selected cluster,

positive differences are obtained when comparing the

complete set of membership functions and a reduced

set grouped by shape-similarity.

The cluster selected for fusion is further processed

using set-theoretic operations. Other strategies are ex-

posed for further consideration.

The proposed similarity measure could be ex-

tended in order to take into account other shape char-

acteristics like the core length (e.g., a triangular mem-

bership function and a trapezoidal membership func-

tion with a tiny core).

This proposal settles some opportunities for future

work on different areas where diverse points of view

are present like group decision-making and suitability

analysis. Some application areas like fuzzy control,

based on this proposal (e.g., to ﬁnd similarities on rule

engines) among other applications could be explored.

ACKNOWLEDGEMENTS

This research is supported by Escuela Superior

Polit

ecnica del Litoral (ESPOL) and it is ﬁnanced by

Secretar

ıa de Educaci

on Superior en Ciencia y Tec-

nolog

ıa (SENESCYT) under Ph.D. studies 2012.

REFERENCES

Bouchon-Meunier, B. and Rifqi, M. (1996). Towards gen-

eral measures of comparison of objects. Fuzzy Sets

and Systems, 84:143–153.

Dice, L. R. (1945). Measures of the Amount of Ecologic

Association Between Species. Ecology, 26(3):297–

302.

Dubois, D. and Prade, H. (1980). Fuzzy Sets and Systems:

Theory and Applications. Academic Press, Inc.

Dujmovi

c, J. and De Tr

e, G. (2011). Multicriteria meth-

ods and logic aggregation in suitability maps. Inter-

national Journal of Intelligent Systems, 26(10):971–

1001.

Jaccard, P. (1908). Nouvelles recherches sur la distribution

ﬂorale. Bulletin de la Soci

ete Vaudense des Sciences

Naturelles, 44:223–270.

Johany

ak, Z. and Kov

acs, S. (2005). Distance based sim-

ilarity measures of fuzzy sets. Proceedings of SAMI,

Kacprzyk, J., Fedrizzi, M., and Nurmi, H. (1992). Group

decision making and consensus under fuzzy prefer-

ences and fuzzy majority. Fuzzy Sets and Systems,

49(1):21–31.

Klir, G. J. and Yuan, B. (1995). Fuzzy Sets and Fuzzy Logic:

Theory and Applications. Prentice Hall.

Le Capitaine, H. (2012). A relevance-based learning model

of fuzzy similarity measures. IEEE Transactions on

Fuzzy Systems, 20(1):57–68.

Lee-Kwang, H., Song, Y.-S., and Lee, K.-M. (1994). Sim-

ilarity measure between fuzzy sets and between ele-

ments. Fuzzy Sets and Systems, 62(3):291–293.

Merig

o, J. and Casanovas, M. (2010). Decision mak-

ing with distance measures and linguistic aggregation

operators. International Journal of Fuzzy Systems,

12(3):190–198.

Rodr

ıguez, R. M., Mart

ınez, L., and Herrera, F. (2012).

Hesistant Fuzzy Linguistic Term Sets for Decision

Making. IEEE Transactions on Fuzzy Systems,

20(1):109–119.

Tversky, D. (1977). Features of similarities. Psychological

Review, 84:327–352.

Xuecheng, L. (1992). Entropy, distance measure and simi-

larity measure of fuzzy sets and their relations. Fuzzy

Sets and Systems, 52(3):305–318.

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

408

Zadeh, L. (1965). Fuzzy sets. Information and control,

8(3):338–353.

Zadeh, L. (1971). Similarity relations and fuzzy orderings+.

Information sciences, 3(2):177–200.

Zwick, R. and Carlstein, E. (1987). Measures of similarity

among fuzzy concepts: A comparative analysis. In-

ternational Journal of Approximate, pages 221–242.

SimilarityofMembershipFunctions-AShapedbasedApproach

409