Multi-agent Solution for ‘8 Queens’ Puzzle

Ivan Babanin

, Ivan Pustovoj

, Elena Kleimenova

, Sergey Kozhevnikov

, Elena Simonova

Petr Skobelev

and Alexander Tsarev

Software Engineering Company «Smart Solutions», Ltd., Samara, Russia

Institution of the Russian Academy of Sciences Institute for the Control of Complex Systems of RAS, Samara, Russia

Keywords: 8 Queens Problem, Evolutionary Computing, Multi-agent Technology, Strategy of Conflict’s Resolving,

Domain Ontologies, Experimental Data.

Abstract: The problem of 8 Queens is one of the most well-known combinatorial problems. In this article multi-agent

evolutionary-based solution for ‘8 Queens’ problem is proposed. In the multi-agent solution each Queen (or

other chess-man) gets a software agent that uses a 'trial-and-error' method in asynchronous and parallel

decision making on selecting new position for queens. As the result the solution is found in distributed

manner without main control center that provides a number of benefits, for example, introducing new types

of chess-man or changing constraints in real time. Two main strategies of Queen’s decision making process

has been considered and compared in experiments: random generation of the next move and conflict-solving

negotiations between the agents. Experiments’ results show significant acceleration of the decision making

process in case of negotiation-based strategy. This solution was developed for training course for students of

Computer Science as a methodical basis for designing swarm-based multi-agent systems for solving such

complex problems as resource allocation and scheduling, pattern recognition or text understanding.

1 INTRODUCTION

Multi-agent technology could be reviewed as a new

generation of object-oriented programming

(AgentLink, 2012). Multi-agent system (MAS)

consists of agents – autonomous software objects

that can analyze the situation, make goal-driven

decisions and communicate with each other

(Wooldridge, 2009). MAS forms a new framework

for evolutionary computing and distributed problem

solving for very complex problems that can’t be

currently solved by existing mathematical methods

and tools. There are several approaches (Bonabeau,

2000) how to build multi-agent systems with direct

or indirect communications. In our paper we will

compare these two basic approaches and show that

coordination between agents helps to reach solution

faster.

In our concept agents will use ‘trial-and-error‘

method and select the first appropriate decision

(‘try‘) which allows improving the situation is being

made, but then – in case of conflicts – the decision

could be revised. Any decision of agent changes

situation for other agents triggering new decision

making process with direct or indirect

communications. In contrast to traditional

centralized, monolithic and sequential solutions

swarm-based approach requires finding right balance

of many conflicting interests of players involved

with the view that new players with new conflicting

interests can arrive at any time. In the paper we

propose to use a well-known ‘8 Queens’ puzzle as a

basis for programmer’s experincing with

methodology of evolutional computing in complex

problem’s solving. Instead of classical combinatorial

search-based method we propose to create agents of

Queens and develop strategies for solving conflicts

in real time. The results of this study are used in

solving complex problems for resource allocation,

scheduling and optimization (Skobelev, 2011).

2 ‘8 QUEENS’ PROBLEM AND

APPROACH TO ITS SOLVING

The ‘8 QUEENS’ puzzle is the problem of putting

eight chess queens on an 8×8 chessboard in such a

way that none of them is able to capture any other

using the standard chess queen's moves. It is known

that there are only 12 fundamentally different

278

Babanin I., Pustovoj I., Kleimenova E., Kozhevnikov S., Simonova E., Skobelev P. and Tsarev A..

Multi-agent Solution for ‘8 Queens’ Puzzle.

DOI: 10.5220/0004148502780281

In Proceedings of the 4th International Joint Conference on Computational Intelligence (ECTA-2012), pages 278-281

ISBN: 978-989-8565-33-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

solutions (and 92 in general) for this puzzle on 8x8

chessboard and there are a lot of classical algorithms

in literature which implement traditional

combinatorial search to find appropriate solutions.

But these methods have some restrictions, for

instance, some of them are applicable for fixed

number of Queens only, some are too complex for

computations, some are hard to modify, etc. (Eight

queens puzzle, 2012).

We will make the classical problem statement

even more complex by introduction of the following

new requirements:

 It is possible to introduce new classes of chess-

men without solution re-programming;

 Enable users to add and remove figures on board

in real-time by user interventions;

 Change preferences and constraints of any agent,

for example, putting constraints on chessmen move

direction;

 Support interactive mode for users which will be

able to re-configure queens positions at any moment

of time;

 Set time constraint on solution finding. The

system will provide intermediate solutions in case of

lack of time, with minimum of conflicts on

chessboard;

 Provide programmers the opportunity to

influence agents intelligence by modify decision

making logic.

Our approach provides a multi-agent solution for ‘8

Queens’ problem with no main ‘control’ center

which analyzes the whole situation on the board and

makes decisions for each Queen. On the contrary,

autonomous software agent is acting on behalf of

each Queen. Agents work as a state machines (in

fact, co-routines) which get control from the multi-

agent dispatcher on each step.

When all agents make their movements they find

that the solution is partial and incomplete because

solution has many unresolved conflicts. Then agents

start to improve the solution by revealing and

resolving conflicts between each other. Two main

strategies of are proposed:

 Random moving: if the agent of queen detects a

conflict (it attacks other Queen or is being attacked

by another chess-man), agent will find available free

positions to go and then select one of them

randomly;

 Conflict negotiations: at first, each Queen tries to

recognize conflicts with others; then negotiations

should help to find a coordinated decision on who

must move and where to go. Such kind of

intelligence allows finding more suitable solutions

faster.

As the result solution is being produced as a set of

trial-and-errors and trade-offs between chess-men as

it takes place in all complex problems.

3 MAS SOLUTION

A conceptual model of problem domain should be

described in the form of ontology that contains a set

of concepts and relationships (SemanticWeb, 2012).

The basic entity of our ontology ‘Queens’ is a

‘Chesspiece’ concept, with 6 successors (Figure 1).

‘Chesspiece’ is an abstract class, so the logic of

behavior should be specified in the successors.

Figure 1: Concepts and relationships of ontology.

By placing the chess-men on certain positions in

the system, the user creates a scene that could be

then executed dynamically. So the Queens are being

placed in accordance with the rules specified in

ontology. Each chesspiece has its own way of attack

that is taken into account in logics of agents.

If some chesspiece becomes a subject or an

object of an attack, it should go to another position.

Search for available positions could be executed as

follows: first, agent will try to find position where a

chesspiece will not have a conflict with any other

chesspiece; if it is impossible, chesspiece will go to

position with minimal number of conflicts, or stay

on initial place.

Logic of the agents’ behavior could be specified

by ‘Attacks’ attribute in the ontology, which is used

in agent’s methods implementation of the decision

making strategy and logic of new position search.

For example, Knight is known to attack positions

one line away horizontally from itself and two lines

away vertically. Thus, the behavior of chesspieces

could be described by the set of pairs consisting of

horizontal and vertical distances from the current

position. For Knight it is {(1, 2), (2, 1)}. Similarly,

we can describe logic of other chesspieces.

To implement generic logic of different

chesspieces just one type of agent is being used:

Multi-agentSolutionfor'8Queens'Puzzle

279

ChessmateAgent. ChessmateAgent could be ordinary

agent of chesspiece, or ‘observer’.

Observer is an agent who, in contrast to ordinary

agents, is not taking part in decision making but

collects information about conflicts from ordinary

agents and on this base can stop the scene and report

data to user.

Observer and ordinary agents independently

from the strategy of conflict’s resolving store

positions of all other chess-men in local memory.

Scene representation in agent’s local memory is

more efficient than the usage of special ‘scene’

agent which should be contacted by each agent of

chess-men on each step, from the point of view of

processor speed.

As it was mentioned above two main strategies

of conflict’s resolving were implemented in the

system. In accordance with the random move

strategy agent makes decision where to go

randomly. Let’s consider negotiations in case of

second strategy of negotiations:

1) Agent starts negotiation strategy for decision

making.

2) Agent prepares list of conflicting chess-men.

3) The first conflicting chess-men is being selected

and the message about number of conflicts is sent to

it (ConflictsCountMessage).

4) Selected chesspiece after receiving the message,

compares the number of conflicts with own number

of conflicts. If own number of conflicts is greater or

equal than received, the chesspiece goes to another

position. In other case, counter-part should make a

move.

5) Agent returns the control to dispatcher.

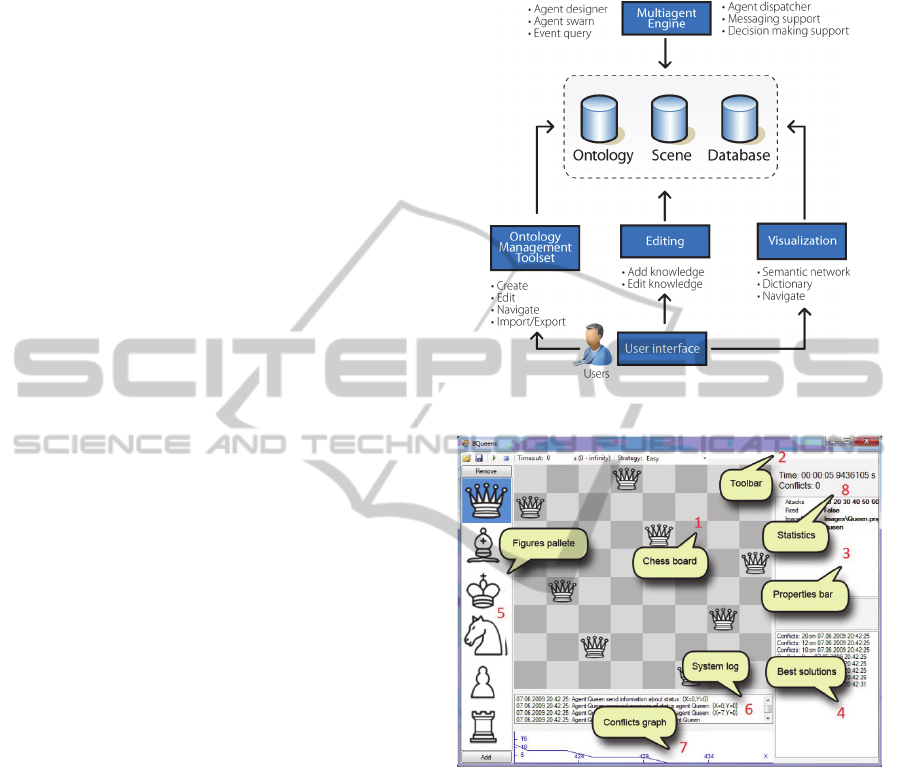
Architecture of multi-agent solution for ‘8 Queens’

problem has been shown in Figure 2. The following

components are presented in the system’s

architecture: multi-agent run-time engine including

dispatcher and messaging system; module of agent’s

construction and logic; storage of ontologies and

scenes, containing all knowledge about class and

current state of the problem being solved; database

for temporary storing of intermediate and final

solutions; visualization tools that allow users to

review the information about the problem being

solved; ontology editor and scene editor; user

interface (Figure 3).

Users can introduce new classes of chess-men,

change position of chess-men, add/delete chess-men,

set time constraints, choose strategy of decision

making, change attributes of chess-men, make step-

back to previous solution. In the process of

computations user can see the best solutions, the log

of agents’ negotiations and the diagram with number

of conflicts in scene.

Figure 2: Architecture of the system.

Figure 3: User interface.

4 EXPERIMENTS WITH

STRATEGIES

During decision making process, the intermediate

positions for scene are being evaluated in the system

– when some agents are in conflict state and others

are not.

User can fix the positions the Queens and then

create new conflicts by moving some of them. Then

start scene again. Selected Queens will be fixed, but

free Queens will find other safe positions, and

solution will be generated again.

In some cases the ‘Queens’ problem solution

needs quite a lot of time. For example, if it is

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

280

required to solve ‘9 Queens’ problem in following

initial position. For some cases there is no solution

at all, for example, for 9 queens on 8x8 chess board.

To find acceptable solution using the finite time

interval in this case, user can specify the time

constraint by special tool on the Control Panel.

After the end of the time limit specified by

constraint, the solution or the scene with the minimal

number of conflicts, i.e. partial solution, will be

shown. After restart the solution could be improved

because of possibility that some of the recently

generated scenes could have less number of conflicts

than previously processed at the preceding iteration.

After getting intermediate solution user can try to

improve it manually. This method allows avoiding

infinite loop of the positioning algorithm.

In the developed system it is also possible to play

with arbitrary number of chess-men on the board

(more than 8).

As it was mentioned above, user can change the

basic strategy interactively. Let’s compare two

strategies: random strategy and strategy with

negotiations for coordinated decision making.

Experiment was carried out on the following

hardware configuration:

 CPU: Intel Core 2 Duo T5450 @ 1.66 GHz;

 RAM: 2 Gb DDR2-667;

 OS: Windows 7 RC1.

We received the following time data for two

different strategies of conflict resolving and 7

different initial positions of 8 Queens – Table 1.

Table 1: Experimental data.

Scene

experiment

Random

selection (ms)

Simple

negotiations (ms)

1 2449 562

2 8127 390

3 1762 343

4 11419 327

5 3120 405

6 2792 795

7 2184 780

The table shows that the results based on

coordinated decision making allowed to accelerate

problem solving in 4 times in comparison to random

strategy and made the solution process more stable,

productive and efficient.

Thus, changes in the number of conflicts during

the decision making process, were studied

separately. The initial scenes for the experiments

were created randomly. The number of conflicts and

total time required (ms) was stored for each scene.

Furthermore, for the better reliability scenes with

partial fixation of chess-men positions, and scenes

with the number of chesspieces greater than 8, were

proceed additionally. As a next step we are going to

study the use of more sophisticated strategies.

5 CONCLUSIONS

Multi-agent solution for ‘8 Queens’ problem was

developed to demonstrate the important advantages

of the evolutional approach implemented by the

multi-agent technologies. The developed system is

used for the training course on Computer Science

aimed to methods of complex problems’ solving

using multi-agent technologies. The main objective

of this work is to show how ‘swarm intelligence’

formed and supported by coordinated decision

making helps to solve complex problems in more

flexible, efficient and faster way.

Future work will be focused on the development

of the agents’ logic editor, elements of self-learning

of the agents, more complex strategies of conflicts

resolving, improvement of the GUI and other

modifications – to make system more intelligent,

visual and interactive.

REFERENCES

AgentLink (2012). [online] Available at:

<http://www.agentlink.org/> [5 April 2012].

Wooldridge, M., 2009. An Introduction to Multiagent

Systems, John Wiley&Sons. London, 2

edition.

Bonabeau, E., Theraulaz, G., 2000. Swarm Smarts.

Scientific American, vol. 282, no. 3, pp. 54-61.

Skobelev, P., 2011. Multi-Agent Systems for Real Time

Resource Allocation, Scheduling, Optimization and

Controlling: Industrial Application. In HoloMAS’11,

10th International Conference on Industrial

Applications of Holonic and Multi-Agent Systems.

Springer. Berlin. pp. 1-15.

Eight queens puzzle (2012), Wikipedia. [online] Available

at: <http://en.wikipedia.org/wiki/8_queens_problem>

[10 April 2012].

SemanticWeb (2012), Wikipedia. [online] Available at:

<http://en.wikipedia.org/wiki/Semantic_web> [20

March 2012].

Multi-agentSolutionfor'8Queens'Puzzle

281