Experiments and Design of an Inference Fuzzy System
F. Benmakrouha, C. Hespel, E. Monnier and D. Quichaud
Computer Sciences INSA, Rennes, France
Keywords:
Fuzzy System, Diabetes, Datum Plane Covering.
Abstract:
The aim of this paper is to propose a criterion to estimate the design, from experimental data, of a fuzzy infer-
ence system, when data are sparse. This lack of data is important and may improve the generalisation ability
of fuzzy systems (Isao Ishibuchi, 2002).
Several methods have been proposed to obtain automatic fuzzy rules from sparse training data. In (Cruz
Vega Israel, 2010), the authors first construct fuzzy rules from collect data. Then, they use kernel regressions
for generate training data.
Another technique used when classical inference methods produce sparse fuzzy rules is a diffusion proce-
dure based on interpolation to initialize incomplete rules (Benmakrouha, 1997), (Glorennec, 1999), (Baranyi,
1996). Our method has the advantage of occuring before initialization step and therefore avoiding unfired
rules which make difficult to produce an accurate output.
1 INTRODUCTION
The lack of data is important and is pointed out by
M Lutaud-Brunet in (Lutaud, 1996). Sugeno and Ya-
sukawa underline in (Sugeno and Yasukawa, 1993)
how difficult it is to build a fuzzy model when data are
scarce and membership functions don’t sweep over all
the universe of discourse. This may improve the gen-
eralisation ability of fuzzy systems (Isao Ishibuchi,
2002).
Several methods have been proposed to obtain au-
tomatic fuzzy rules from sparse training data.
In (Cruz Vega Israel, 2010), the authors first con-
struct fuzzy rules from collect data. Then, they use
kernel regressions for generate training data.
Another technique used when classical inference
methods produce sparse fuzzy rules is a diffusion
procedure based on interpolation to initialize incom-
plete rules (Benmakrouha, 1997), (Glorennec, 1999),
(Baranyi, 1996).
The objective of this paper is to measure the im-
pact of datum plane covering on the outcome of a
fuzzy inference system. Most of optimization meth-
ods make the assumption that datum plane is suffi-
ciently covered. If this assumption no longer holds,
we will see that these methods cannot work, since it
implies that, before optimization, the fuzzy system gi-
ves acceptable results. In (Benmakrouha et al., 2010),
we analysed the relationship between learning set Ω
and labels of fuzzy inference system. In this paper,
we take into account a data density repartition, by the
measure of number of available data on intervals of
each input variable domain.
All these tecniques take place during optimisation
step when our method is used before initialization
step. This in turn allows one to isolate unfired rules
and to proceed, if necessary, to a partial remodelling
of the FIS before training and optimization.
2 THE TAGAKI-SUGENO MODEL
The model under consideration in this section is
a Tagaki-Sugeno model, which corresponds to dis-
cretized linear models of order 1, combined with non-
linear functions.
y(t) =
r
∑
i=1
h
i
(z(t))(a
i
1
.y(t −idecal)+b
i
1
.u(t −idecal))
y(t) is the output,
r is the number of linear models,
z(t) a vector which depends lineary or not on the
state,
h
i
(z(t)) >= 0 , i = 1, ··· , r nonlinear functions
verifying the convex sum property.
420
Benmakrouha F., Hespel C., Monnier E. and Quichaud D..
Experiments and Design of an Inference Fuzzy System.
DOI: 10.5220/0004148904200423
In Proceedings of the 4th International Joint Conference on Computational Intelligence (FCTA-2012), pages 420-423
ISBN: 978-989-8565-33-4
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

idecal is the time lag between input and its effect,
which is specially interesting in our application.
We have measures about every five minutes and
we admit that the effect of insulin (considered in
our application)is fast and noticeable ten (idecal=2)
minutes later, up to half an hour(idecal = 6).
The determination of unknown parameters a
i
1
and
a
i
2
is done by the algorithm of recursive least square.
3 APPLICATION TO THE
INSULIN/GLYCAEMIA
BEHAVIOR OF DIABETICS
3.1 The Available Data
The correlated data ”‘insulin infusion deliv-
ery/glycaemia”’ has been provided by the team
of Pr. Pinget, CHU of Strasbourg. They concern the
same person and the same insulin.The insulin infu-
sion has been done by an intra-peritoneal route and
the glycaemia has been checked by a subcutaneous
sensor. Measures of glycaemia have been made every
five minutes during 7 days, which corresponds to
1700 measures.
A bolus is a dose of insulin infused manually, in ad-
dition to the basic dose, since postprandial glycemia
cannot be regulated satisfactorily. The insulin file
contains crude data about basic insulin doses as well
as boluses. So, a pretraitement of the insulin file has
been necessary to produce a file of insulin delivery
for the same person every five minutes.
3.2 Experiments and Validation of the
Model
The learning set is composed of the first mea-
sures(280 points) that corresponds to insulin infusion
and blood glucose concentration of a patient during a
day. We take 7 (r = 7)linear models, considering that
each model is valid about three and half hours. The
mean square error(MSE)is calculated on the totality
of the measures(1700 points).
We make experiments by changing the parameter
idecal of the model, time lag between an input and its
effect.
The test of our modeling method shows that we
can predict the glycaemia over a long period (7 days),
by considering glycaemia and insulin delivery 15-
minute (resp 30-minute) before with an error of about
6%(resp 16%), which is a good result compared with
current results. However, we see that results obtained
Table 1: First table.
r idecal MSE
7 2 0.04
7 3 0.06
l
7 6 0.16
7 24 1.02
are not so good in the last case, when we consider
slow effect insulin (with 2-hours delay). In this case,
our model has to be refined, by increasing its order.
4 DATUM PLANE COVERING
We propose a measure used to pre-validate a fuzzy
model. We suppose that there exists a learning set
Ω = {(x
j
, d
j
)}, where x
j
is an input vector and d
j
,
the corresponding output. We also assume that the
desired function f is defined in
V = [a
1
, b
1
] × [a
2
, b
2
] × ... × [a
p
, b
p
]
Usually, to validate a fuzzy inference system, the
mean square error (MSE) is calculated on a test set.
If the MSE exceeds a threshold, then training is done,
using a gradient method. This consists in modifying
C
j
at each presentation of examples from the error
(y(x
j
) − d
j
).
Unfortunately, in case of model invalidation, we can-
not determine never learned rules that cause the gap
between the model and the real system. Moreover, if
there is an insufficient covering of datum plane, train-
ing and finer splitting of input space are inefficient
and useless. With the criterion proposed below, we
estimate the datum plane coverage and we are able
to isolate inactivated rules. Then, partial remodeling
of the fuzzy inference system is possible. The study
is investigating the relationship between a quantita-
tive variable X , number of available data for each in-
put, and a qualitative variable Y , labels of membership
functions.
When designing a fuzzy system, we attribute
to each input I r modalities (or labels) noted
y
1
, ··· y
l
, ··· y
r
. We note X
I
the variable for the input I
of average ¯x
I
and variance σ
2
X
I
. We note Ω
I
the cor-
responding learning set . Each label y
l
of I defines
a subset Ω
I
l
of Ω
I
: we obtain a partition of Ω
I
in m
classes. We note n
I
l
= card(Ω
I
l
) and n
I
= card(Ω
I
).
We have n
I
= Σ
m
l=1
n
I
l
. Then, if we consider the re-
striction de X
I
to Ω
I
l
) (l = 1, ··· , m), we may define
ExperimentsandDesignofanInferenceFuzzySystem
421

the average (noted ¯x
I
l
)and the variance (noted σ
2
X
I
l
of
X
I
on this subset:
¯x
I
l
=
∑
ω∈Ω
I
l
X(ω)
n
I
l
σ
2
X
I
l
=
∑
ω∈Ω
I
l
(X(ω) − ¯x
I
l
)
2
n
I
l
We have an index of connection between the datum
plane coverage (for an input I) and the learning set
defined by :
s
I
=
s
σ
2
E
σ
2
XI
where
σ
2
X
I
= σ
2
E
+ σ
2
R
and
σ
2
E
=
∑
r
l=1
n
I
l
∗ ( ¯x
I
l
− ¯x
I
)
2
n
I
and
σ
2
R
=
∑
r
l=1
n
I
l
∗ σ
2
X
I
l
n
I
and
¯x
I
=
∑
r
l=1
(n
I
l
∗ ¯x
I
l
)
n
I
This index of connection consists in detecting rela-
tionships between number of data of the learning set
Ω
I
and r
I
labels. This index is low if the features of
these labels are not so different (Test 1). When this
index is high, it points to that there is a bad repartition
of membership functions (Test 3). This gives an in-
formation about the repartition of data of learning set
Ω
I
between membership functions.
4.1 Experiments
We have made 3 tests for the first input (with two tri-
angular membership functions) using our application.
We give in these array the features of these functions.
We obtain for the first test a low index(0.035), the sec-
ond a medium index (0.28) and for the last test a high
index (0.84). In the third test, the first membership
function is useless and the corresponding rules are in-
actived. So, we can suppress them without affecting
results. We have made a 4th test where three (out of
four) membership functions and the associated rules
were unnecessary.
Table 2: First membership function.
Test Center Left corner Right corner
1 1.4 1.6 1.0
2 1.0 0.6 1.0
3 0.2 0.2 0.2
Table 3: Second membership function.
Test Center Left corner Right corner
1 2.6 1.0 0.9
2 2.6 1.0 0.9
3 3.0 2.8 0.5
4.2 Graphic Representation
We represent sets of data by Box & Whiskers Plots
to underline the relation between number of data and
labels of membership functions. The first figure (resp
figure 2 and figure 3) corresponds to Test1 (resp Test
2 and Test 3).
Figure 1.
5 CONCLUSIONS
We have proposed a measure for detecting useless
rules and thus pre-validating a fuzzy inference sys-
tem. When the model is not pre-validated, we have
not to carry out next steps, particularly optimization
step.
We have shown that this criterion gives useful in-
formation about datum plane coverage.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
422

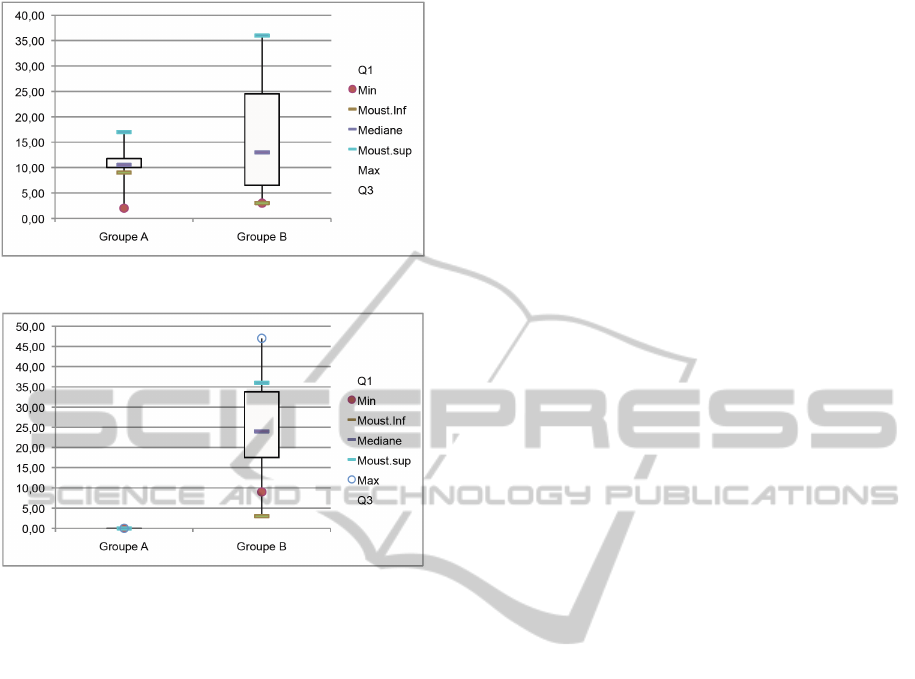
Figure 2.
Figure 3.
REFERENCES
Baranyi, P. K. (1996). A general and specialised solid cut-
ting method for fuzzy rule interpolation. J. BUSEFAL
URA-CNRS, 66:13–22.
Benmakrouha, F. (1997). Parameter identification in a fuzzy
system with insufficient data. In Sixth IEEE Inter-
national Conference on Fuzzy Systems, volume 542,
page 1:537.
Benmakrouha, F., Hespel, C., and Monnier, E. (2010). An
algorithm for rule selection on fuzzy rule-based sys-
tem applied to the treatment of diabetics and detection
fraud in electronic payment. In FUZZ-IEEE.
Cruz Vega Israel, W. Y. (2010). Multiple fuzzy neural net-
works modeling with sparse data. Neurocomputing,
pages 2446–2453.
Glorennec, P. Y. (1999). Algorithmes d’apprentissage pour
syst
`
emes d’inf
´
erence floue. Paris France Herm
`
es.
Isao Ishibuchi, T. Y. (2002). Performance evaluation of
fuzzy partitions with different fuzzification grades. In
Proceedings of the 2002 IEEE International Confer-
ence Fuzzy Systems FUZZ-IEEE’02.
Lutaud, M. (1996). Identification et Contr
ˆ
ole de proces-
sus par r
´
eseaux Neuro-Flous. PhD thesis, Universit
´
e
d’Evry Val d’Essonne.
Sugeno, M. and Yasukawa, T. (1993). A fuzzy-logic-based
approch to qualitative modeling. IEEE Trans. on
Fuzzy Systems, 1(1).
ExperimentsandDesignofanInferenceFuzzySystem
423