
Image Halftoning with Turing Patterns
Atsushi Nomura
Faculty of Education, Yamaguchi University, Yoshida 1677-1, Yamaguchi 753-8513, Japan
Keywords:
Image Processing, Halftoning, Reaction-diffusion, Turing Pattern, Long-range Inhibition, PDE Approach.
Abstract:
This paper presents an image halftoning algorithm with a reaction-diffusion system in which periodic patterns
called Turing patterns autonomously emerge. Image halftoning refers to conversion of a gray level image to
a binary image so that the human visual system can perceive the original gray level image from the converted
binary one. The reaction-diffusion system has activator and inhibitor distributions, and creates the Turing
type periodic patterns in the distributions from an initial noisy distributions under the condition of long-range
inhibition. Characteristics of the Turing patterns depend on a parameter of the reaction-diffusion system.
Thus, by modulating the parameter distribution according to an image brightness distribution, the proposed
algorithm creates Turing patterns of which characteristics distribute spatially; the human visual system can
perceive distribution of the Turing patterns as the original image. Application of the proposed algorithm to a
test image demonstrates its qualitative performance and convergence.
1 INTRODUCTION
Application of Turing patterns to computer graph-
ics and image processing is an interesting topic from
a biological point of view. Some animals have pe-
riodic patterns on their skin surface (Shoji et al.,
2002). Turing originally proposed a scenario ex-
plaining how biological systems organize stable pe-
riodic patterns (Turing, 1952). He considered a
reaction-diffusion system consisting of two diffusion
processes coupled with some reaction functions on
activation and inhibition, and showed that strong
diffusive coupling or long-range inhibition causes
the periodic patterns. The periodic patterns au-
tonomously emerge from initial noisy distributions in
the reaction-diffusionsystem under the long-range in-
hibition. Since it is possible to numerically compute
the reaction-diffusion system, Witkin and Kass pro-
posed to apply Turing type periodic patterns to com-
puter graphics for drawing patterns observed on ani-
mal skin surfaces (Witkin and Kass, 1991).
Image halftoning refers to conversion of a gray
level image to a binary image; that is a kind of image
quantization. A simple algorithm for image halfton-
ing is binarization with a fixed threshold level for im-
age brightness. However, halftoning algorithms are
required to create binary images that can be perceived
as their original gray level images by the human vi-
sual system. The simple binarization algorithm does
not satisfy this requirement. Thus, there have been
proposed many halftoning algorithms (Lau and Arce,
2008), eg pattern dithering algorithm, error diffusion
algorithm and a direct binary search algorithm. Re-
cently, Schmaltz et al. proposed a physics-based
halftoning algorithm, which utilizes an electrostatic
phenomenon (Schmaltz et al., 2010).
If focusing on nature inspired algorithms in im-
age processing, we can find interesting work on im-
age segmentation. For example, Kuhnert demon-
strated that a two-dimensional light-sensitive chemi-
cal reaction-diffusionsystem works as image segmen-
tation (Kuhnert et al., 1989). However, the chemical
reaction system did not satisfy the condition of the
long-range inhibition; it did not create stable results
of image segmentation. The segmentation result tran-
siently emerged as time proceeds. In addition, since
the image segmentation was the simple binarization,
we did not perceive the result as the original image.
The purpose of this research work is to present a
novel halftoning algorithm with Turing patterns cre-
ated by a reaction-diffusion system under the long-
range inhibition. Characteristics of periodicity and
average level on the Turing patterns depend on a pa-
rameter of the reaction-diffusion system. In two-
dimensional space, the periodic patterns appear as cir-
cular patterns. Thus, by modulating the character-
istics of periodicity and average level according to
image brightness distribution, the algorithm converts
286
Nomura A..
Image Halftoning with Turing Patterns.
DOI: 10.5220/0004149202860289
In Proceedings of the 4th International Joint Conference on Computational Intelligence (ECTA-2012), pages 286-289
ISBN: 978-989-8565-33-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

image brightness levels to different Turing type peri-
odic patterns. When a local area has pixels of higher
brightness level, it is filled with high density of larger
white circular patterns; when a local area has pix-
els of low brightness level, it is filled with low den-
sity of small white circular patterns. Spatial distri-
butions of these different periodic (circular) patterns
bring brightness perception of the original image for
the human visual system. Application of the proposed
algorithm to a test image demonstratesqualitativeper-
formance and convergence of the algorithm, in com-
parison with previous representative algorithms.
2 THE ALGORITHM
2.1 Reaction-diffusion System and
Turing Patterns
A reaction-diffusion system generally consists of
time-evolving partial differential equations of dif-
fusion equations coupled with reaction functions.
Schnakenberg proposed a reaction-diffusion system
consisting of the following set of equations with two
distributions: activator u(x,y,t) and inhibitor v(x,y,t)
defined in a two-dimensional space (x,y) and time
t (Schnakenberg, 1979), as follows:
∂u
∂t
= ∇
2
u+ γ(a− u+ u
2
v) (1)
∂v
∂t
= D∇
2
v+ γ(b− u
2
v) (2)
in which ∇
2
is a two-dimensional Laplacian operator
and D is a diffusion coefficient on v(x,y,t); a, b and
γ are constants; a diffusion coefficient on u(x,y,t) is
fixed at 1.0. The reaction-diffusion system described
with Eqs. (1) and (2) creates periodic patterns on the
two distributions u and v, when the inhibitory diffu-
sion coefficient D is much larger than the activatory
one (D ≫ 1) and their initial conditions are as fol-
lows:
u(x,y,t = 0) = a+ b+ n
1
(3)
v(x,y,t = 0) =
b
(a+ b)
2
+ n
2
(4)
in which n
1
and n
2
are random noise. Turing patterns
refer to periodic patterns emerging in the reaction-
diffusion system under the condition of D ≫ 1, that is,
under the condition of the long-rangeinhibition due to
the strong inhibitory diffusion. The noise components
n
1
and n
2
added to u = a+ b and v = b/(a+ b)
2
ini-
tiate emergence of the Turing patterns. Equations (1)
0.0
1.0
2.0
3.0
0.0 1.0 2.0 3.0
u,v
u
v
x
(b)
0.0
1.0
2.0
3.0
0.0 1.0 2.0 3.0
u,v
u
v
x
(a)
0.0
1.0
2.0
3.0
0.0 1.0 2.0 3.0
u,v
u
v
x
(c)
Figure 1: Three examples of one-dimensional Turing pat-
terns created with Eqs. (1) and (2) with (a) b = 0.50, (b) b =
1.00 and (c) b = 1.50. Solid lines indicate spatial distri-
butions of u(x,t = 5.0) and broken lines indicate those of
v(x,t = 5.0). Equations (3) and (4) provided initial con-
ditions of u and v. Other parameter settings were fixed
at a = 0.025,D = 20,γ = 1.0 × 10
3
,δh = 1.0 × 10
−2
and
δt = 1.0×10
−5
.
and (2) can be solved numerically with a finite differ-
ence method with a spatial difference δh and a tem-
poral difference δt.
Figure 1 shows three examples of one-
dimensional Turing type periodic patterns created
with Eqs. (1) and (2). Initial distributions of Eqs.(3)
and (4) became unstable and spatial periodic patterns
autonomously emerged. Interestingly, spatial wave
length of the periodic patterns depends on the param-
eter b; a lager value of b brought shorter wave length.
In addition, a smaller value of b brought a larger
value of v in comparison with a smaller value of u.
That is, it is possible to modulate the wave length and
the difference between the average levels of u and v
with modulation of the parameter b.
ImageHalftoningwithTuringPatterns
287

(a) (b) (c)
(d) (e) (f)
Figure 2: Results of halftoning for the gray level image LENA (Wakin, 2003). (a) Original image with the size of 512 ×
512 (pixels) and 256 brightness levels; (b) a distribution of u(x,y,t = 10) created by Eq. (1); (c) a distribution of v(x,y,t = 10)
created by Eq. (2); (d) a halftone image H(x, y,t = 10) created by the proposed algorithm; (e) a halftone image created by an
error diffusion algorithm; (f) a halftone image created by a pattern dithering algorithm. Parameter settings of the proposed
algorithm were a = 0.025,b
min
= 0.50,b
max
= 1.50,D = 20,γ = 1.0× 10
3
,δh = 0.05 and δt = 1.0 × 10
−5
. The results (e)
and (f) were created by an image processing software (Adobe Photoshop CS4) for comparison.
2.2 Image Halftoning
Upon the one-dimensional experimental results of
Fig. 1, this paper proposes an image halftoning algo-
rithm by employing the Schnakenberg type reaction-
diffusion system (Schnakenberg, 1979) under the
long-range inhibition. Since the characteristics of the
Turing patterns depend on the parameter b, the algo-
rithm linearly modulates the parameter value of b ac-
cording to a normalized image brightness distribution
I(x,y), as follows:
b(x,y) = b
min
+ (b
max
− b
min
)I(x, y) (5)
in which b
min
and b
max
are the minimum and maxi-
mum values of b.
The image halftoning algorithm consists of the
following three steps. In the first step, we prepare the
initial conditions of u and v described with Eqs. (3)
and (4). In the second step, we numerically compute
temporal developments of u(x,y,t) and v(x, y,t) with
the reaction-diffusion system of Eqs. (1) and (2), in
which the parameter b spatially distributes according
to Eq. (5). In the final step, after sufficient duration of
time, we create a halftoning image H(x,y,t) with
H(x,y,t) =
1 if u(x,y,t) ≥ v(x, y,t)
0 otherwise
(6)
in which H = 1 indicates a white pixel and H = 0
does a black pixel. Recall that a smaller value of b
brings a longer wave length of periodic pattern and
a larger average level of v, and thus the area having
smaller values of b filled with high density of black
pixels (see also Fig. 1).
3 EXPERIMENTAL RESULT
This section presents an example of image halfton-
ing with the proposed algorithm. Figure 2 shows a
halftone image created by the proposed algorithm for
the gray level image LENA (Wakin, 2003), in com-
parison with two other representative algorithms of
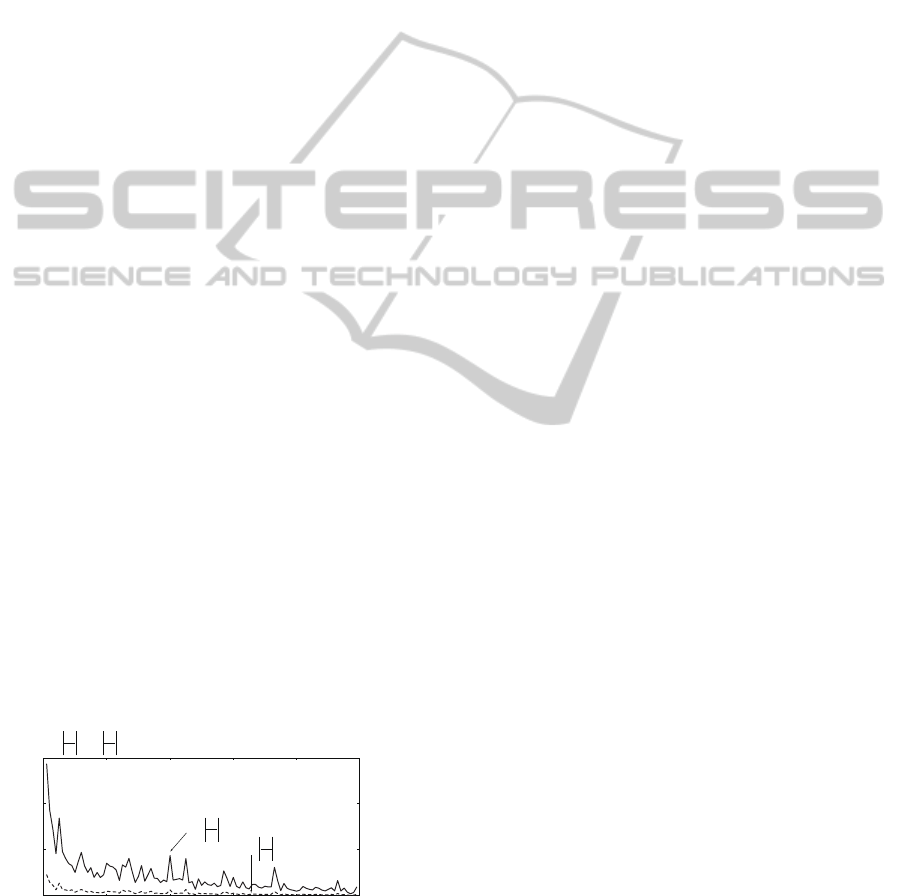
halftoning. Figure 3 shows temporal changes of u and
v in the proposed algorithm. Computation time of the
proposed algorithm was four and half hours on a stan-
dard computer system with an Intel CPU.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
288
We can roughly perceive the original image from
the halftone image created by the proposed algorithm
[Fig. 2(d)]. Thus, the proposed algorithm would be
better than a simple binarization algorithm. When
comparing the halftone image with that of the er-
ror diffusion algorithm [Fig. 2(e)], we recognize that
quality of the image created by the proposed algo-
rithm is insufficient. We can state that the proposed
algorithm roughly achieved its convergence as shown
in Fig. 3, and the algorithm needs quite longer compu-
tation time than the previous ones. The convergence
of the algorithm implies that the proposed algorithm
also has the function of image pooling.
Future research work for the proposed algorithm
is as follows. In order to evaluate quantitative per-
formance of the proposed algorithm, we need any
evaluation method for image quality. Kawasaki et
al. proposed a quantitative evaluation method for
halftone image, by modeling the human brightness
perception (Kawasaki et al., 2002). Their method is
one of candidates for quantitative evaluation of im-
age halftoning algorithms. Previous halftoning al-
gorithms were also applied to multi-level and color
halftoning. Extension of the proposed algorithm is
also an interesting topic as an image processing. A
cellular neural network (CNN) approach can imple-
ment a reaction-diffusion system with a circuit sys-
tem (Crounse et al., 1993). We can expect that the
proposed algorithm implemented with CNN performs
in real time. Stable image pooling is also one of ap-
plication areas of the proposed algorithm.
4 CONCLUSIONS
This paper presented a novel halftoning algorithm
with Turing patterns emerging in a reaction-diffusion
system. Characteristics of the Turing patterns depend
on a parameter value of the system. Thus, in order to
convert a gray level image to a binary image, the algo-
0
40
80
120
0 2 4 6 8 10
t
v
t
u
∂
∂
∂
∂
max ,max
t
u
∂
∂
max
t
v
∂
∂
max
t
Figure 3: Temporal changes of max
(x,y)
|∂u/∂t| (the solid
line) and max
(x,y)
|∂v/∂t| (the broken line) computed for the
two distributions of u and v in the process of image halfton-
ing performed for LENA (Wakin, 2003) (see also Fig. 2).
rithm modulated the parameter of the system accord-
ing to image brightness distribution. Although the hu-
man visual system can perceive the resulting halftone
image as its original image, the quality of the halftone
image was poor, in comparison with other previous
representative algorithms. As future research work,
in addition to improvement of image quality and re-
duction of computation time, it is also interesting to
consider how image is represented with a bio-inspired
reaction-diffusion system.
ACKNOWLEDGEMENTS
The present study was partly supported by a Grant-in-
Aid for Scientific Research (C), Japan Society for the
Promotion of Science (JSPS) (No. 23500278).
REFERENCES
Crounse, K. R., Roska, T., and Chua, L. O. (1993). Im-
age halftoning with cellular neural networks. IEEE
Transactions on Circuits and Systems II: Analog and
Digital Signal Processing, 40(4):267–283.
Kawasaki, J., Hayashi, A., and Iijima, T. (2002). Evalua-
tion method of picture quality by two dimensional vis-
sual model and verification of its theory using various
modulated images. IEICE Transactions on Informa-
tion and Systems, J85-D-II(2):228–241. [in Japanese].
Kuhnert, L., Agladze, K. I., and Krinsky, V. I. (1989). Im-
age processing using light-sensitive chemical waves.
Nature, 337:244–247.
Lau, D. L. and Arce, G. R. (2008). Modern Digital Halfton-
ing. CRC Press, New York, USA, second edition.
Schmaltz, C., Gwosdek, P., Bruhn, A., and Weickert, J.
(2010). Electrostatic halftoning. Computer Graphics
Forum, 29(8):2313–2327.
Schnakenberg, J. (1979). Simple chemical reaction systems
with limit cycle behaviour. Journal of Theoretical Bi-
ology, 81:389–400.
Shoji, H., Iwasa, Y., Mochizuki, A., and Kondo, S.
(2002). Directionality of stripes formed by anisotropic
reaction-diffusion models. Journal of Theoretical Bi-
ology, 214:549–561.
Turing, A. M. (1952). The chemical basis of morphogen-
esis. Philosophical Transactions of the Royal Society
of London. Series B, Biological Sciences, 237:37–72.
Wakin, M. (2003). Standard test images – Lena/Lenna.
http://www.ece.rice.edu/˜wakin/images/.
Witkin, A. and Kass, M. (1991). Reaction-diffusion tex-
tures. In Proceedings of the 18th annual conference on
Computer Graphics and Interative Techniques, pages
299–308, Las Vegas, US. ACM.
ImageHalftoningwithTuringPatterns
289
