Memetic Algorithm with Population Management

for the Two-dimensional Loading Vehicle Routing Problem

with Partial Conﬂicts

Khaoula Dhaoui, Nacima Labadie and Alice Yalaoui

LOSI-ICD-UMR-STMR-CNRS, University of Technology of Troyes, Troyes, France

Keywords:

Vehicle Routing, Bin-packing, Partial Conﬂicts, Memetic Algorithm.

Abstract:

The two-dimensional loading vehicle routing problem with partial conﬂicts combines two NP-hard problems:

the capacitated vehicle routing problem (CVRP) and the two-dimensional bin-packing problem with partial

conﬂicts (2BPPC). This problem arises for example in hazardous waste collection, where some materials

can be partially conﬂicting. In this paper, we propose a memetic algorithm with population management to

resolve this new problem. A modiﬁed SHF-D heuristic is used to obtain feasible packing in each vehicle. The

proposed approach is tested on a new benchmark, created by adding partial conﬂicts to instances from the

literature.

1 INTRODUCTION

Some recent works have been dedicated for coupling

vehicle routing and items packing in the vehicles to

obtain solutions for the two-dimensional loading ca-

pacitated vehicle routing problem (2L-CVRP). This

problem was proposed for the ﬁrst time by Iori et

al. (Iori, 2004) who developed an exact method (Iori

et al., 2007) to solve it. Several approximate methods

were proposed by Gendreau et al. (Gendreau et al.,

2008), Zachariadis et al. (Zachariadis et al., 2009),

Leung et al. (Leung et al., 2011), Fueller et al. (Fu-

ellerer et al., 2009) and Duhamel et al. (Duhamel

et al., 2011). In all previous studies, the authors

solved a basic two-dimensional bin-packing problem

for each vehicle.

Khebbache et al. (Khebbache et al., 2011) studied

the 2L-CVRP with time windows. The authors pro-

posed six heuristics and metaheuristics for this vari-

ant. The three dimensional case refereed to as 3L-

CVRP with time windows was also investigated by

Moura et al. (Moura and Oliveira, 2009) and (Moura,

2008).

The concept of distance constraint was introduced

by several authors in studies dedicated to packing

problems. In (Stoyan and Yaskov, 1998), each item

has to be separated from all the other items and from

the bin borders by a given distance, depending on

the item. Therefore, there is no contact between the

edges of all items. These authors (Stoyan and Yaskov,

1998) proposed a mathematical model and a com-

bination of a branch and bound and a reduced gra-

dient method to solve this problem. They consid-

ered both the cases where the items are either rect-

angles or circles. The problem was generalized to

the three dimensional case by Stoyan and Chugay

(Stoyan and Chugay, 2009). In this last study, items

are either cylinders or parallelepipeds and the packing

area is considered of some given shape. In (Beaumont

et al., 2010), the maximal distance between two items

packed in the same bin has to be smaller than a given

threshold.

In some industrial applications such as in Haz-

ardous Material (HazMat) transportation, residues of

HazMat are ﬁrst decanted into rectangular or circu-

lar containers at their source, then the schedule of the

containers transshipment to reprocessing plants is or-

ganized. According to HazMat classiﬁcation, some

products can be partially conﬂicting. In this case

these materials can be stored or shipped together, but

they have to be separated by a given safety distance.

Some HazMat can also be in total conﬂict, it is then

not permitted to store them in the same warehouse or

transport them in the same vehicle. In HazMAt trans-

portation legislation, one horizontal meter distance

have to be kept between any two partially conﬂicting

materials. This industrial application motivated us to

introduce the two-dimensional bin-packing problem

with partial conﬂicts (2BPPC), for which a mathemat-

ical model, several heuristics and a multi-start genetic

189

Dhaoui K., Labadie N. and Yalaoui A..

Memetic Algorithm with Population Management for the Two-dimensional Loading Vehicle Routing Problem with Partial Conﬂicts.

DOI: 10.5220/0004149501890195

In Proceedings of the 4th International Joint Conference on Computational Intelligence (ECTA-2012), pages 189-195

ISBN: 978-989-8565-33-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

algorithm were proposed (Dhaoui et al., 2012).

This paper provides a ﬁrst study for the two di-

mensional loading with partial conﬂicts capacitated

vehicle routing problem (2LPC-CVRP). The resolu-

tion approach proposed here combines a memetic al-

gorithm for the routing problem and a heuristic for

the packing. In Section 2, the two problems (vehi-

cle routing and 2-dimensional bin-packing with par-

tial conﬂicts) are presented. In Section 3, the different

components of the memetic algorithm are explained.

Section 4 is dedicated to computational results and a

conclusion ends this paper.

2 PROBLEM PRESENTATION

2.1 Vehicle Routing Problem

The capacitated vehicle routing problem can be de-

ﬁned on an undirected graph G = (V, E) with V = {0,

1,..., n} the set of vertices and E the set of edges. The

vertex 0 represents the depot, where a ﬂeet of K iden-

tical vehicles with capacity Q is provided, whereas the

other vertices represent the customers. A demand d

is associated to each customer i and a traveling cost

i j

is associated to each edge [i,j].

Given the graph G, the vehicle routing problem

consists in ﬁnding the routes satisfying the following

constraints: each route starts and ends at the depot,

each customer is visited only once by a single vehi-

cle and the total demand of customers assigned to the

same route can not exceed the vehicle capacity Q. The

aim is to minimize the total traveling cost. The objec-

tive function is deﬁned as follows:

∑

k=1

∑

i=1

∑

j=1

i j

(1)

Where x

i j

is a binary variable that takes the value 1

when the edge [i,j] is crossed by the vehicle k going

from i to j.

2.2 Two-dimensional Packing Problem

with Partial Conﬂicts

This problem has been studied for the ﬁrst time by

Dhaoui et al. (Dhaoui et al., 2012). A 2BPPC instance

consists in a set A = {1, ..., n} of items which have to

be packed in a minimum number of identical bins. A

bin is deﬁned by its height H and its width W . An

item i has a height h

and a width w

, w

∈ IN) and

may be in partial conﬂict with some other speciﬁed

items. A solution of the problem consists in assign-

ing each item i to a bin and deﬁning its position, de-

noted by (x

, y

) which corresponds to the coordinates

of its bottom left-hand corner in the bin, without over-

lapping while keeping a safety distance D between

partially conﬂicting items (Figure 1). The considered

distance is denoted d

∞

and is deﬁned as follows: let

i and j be two items inserted in the same bin and as-

sume that their positions in the bin are: (x

, y

) and

, y

). d

∞

(i, j) = max{|x

− x

|, |y

− y

|}.

In this study, the distance d

∞

is chosen because it

is the one often used in hazardous material transporta-

tion. In this sector, the guideline is to keep a preﬁxed

horizontal or vertical spacing between any two ma-

terials partially conﬂicting. For example, corrosive

material and ﬂammable solid material are in partial

conﬂict as indicated in Hazardous material classiﬁca-

tion data-base (Environment Canada, 2002). hence,

when they have to be packed within the same bin (a

storage area or a vehicle), a safety distance of 1 hori-

zontal or vertical meter must separate them. Figure 1

shows the difference on using the distance d

∞

and the

Euclidean distance d.

This study is dedicated to a new problem, the

2LPC-CVRP which is a combination of both vehi-

cle routing optimization and two-dimensional pack-

ing of items with partial conﬂicts. In this work, non-

sequential (unrestricted) packing without items rota-

tion is considered.

Figure 1: Safety distance.

In Figure 2, items 1 and 2 are conﬂicting with item

i, that is why a safety distance D is kept between them.

Figure 2: Partial conﬂicts.

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

190

3 MEMETIC ALGORITHM WITH

POPULATION MANAGEMENT

In this section, the different components of our

memetic algorithm (MA) are detailed. First, an ini-

tial population of NP chromosomes is generated. A

chromosome is coded as a sequence of n customers (a

permutation) without route delimiters, which can be

seen as a giant tour violating the capacity and pack-

ing constraints. A feasible solution of our problem is

obtained by cutting this giant tour into feasible routes

using a Cutting Procedure. The parent solutions are

selected with a binary tournament and crossed over to

obtain child solutions or offsprings. A local search is

applied with a given probability to improve the solu-

tions quality. Finally, the acceptance or rejection of

new solutions is decided by the population manage-

ment procedure. The best NP solutions constitute the

new population. This treatment is repeated NG times.

3.1 Initial Solutions

A ﬁrst solution is computed with an adaptation of

Clarke and Wright heuristic (Clarke and Wright,

1964) and is then converted to a chromosome by con-

catenating its routes. The resulting chromosome is in-

cluded in the initial population which is completed by

generating randomly the (NP -1) remaining elements.

Each chromosome in the population is evaluated us-

ing the cutting procedure explained in section 3.3.

3.2 Crossover

Parents are selected by binary tournament method:

two chromosomes are randomly selected in the popu-

lation and the best one is the ﬁrst parent. This process

is repeated to get the second parent. Then they are

combined using the classical operator OX for Order

Crossover (Goldberg, 1989). OX begins by randomly

selecting two break points i and j (1 < i ≤ j < n) in

the ﬁrst parent. Customers located between the posi-

tions i and j in the ﬁrst parent are copied into the child

chromosome in the same positions. The remaining

customers are added by browsing the second parent

from left to right and are copied in the order of their

appearance. Each crossover provides a single child.

The ﬁtness of the obtained child solution is then com-

puted using the Cutting Procedure.

3.3 Cutting Procedure

This procedure starts by applying the method called

Split proposed by Prins (Prins, 2004) for the CVRP.

Split consists in computing a shortest path in an aux-

iliary graph containing a dummy vertex 0 and a ver-

tex for each customer. The packing feasibility of the

obtained routes is checked with a modiﬁed version

of SHF-D heuristic. Infeasible routes (for the pack-

ing problem) are concatenated to obtain a new gi-

ant route (or a sub-chromosome). For this new se-

quence, a new packing heuristic is performed: cus-

tomers are assigned to routes in the order given by the

sub-chromosome. When the customer’s demand can’t

be packed in all the available vehicles, a new route is

created and this later is initialized with this customer.

A feasible solution for the 2LPC-CVRP is obtained at

the end of this procedure.

3.4 Population Management

To avoid premature convergence of the population to

a local minimum, it is possible to use a management

tool that allows to choose whether to keep or reject

a solution according to a distance criterion from the

existing solutions. Memetic algorithms with popula-

tion management have been introduced by S

orensen

and Sevaux (S

orensen and Sevaux, 2006). We con-

sider the distance computing the number of ”broken

pairs” as introduced in (Mart

ı et al., 2005). Let con-

sider two chromosomes X and Y . The customer that

occupies the position i in the chromosome X is de-

noted X

. The distance D(X,Y ) equals the number of

pairs {X

, X

i+1

} that are not adjacent in Y . The dis-

tance of a chromosome to a population P is deﬁned as

follows:

(Y ) = min{D(X,Y ) : X ∈ P} (2)

A new solution Y is accepted in the population P

if its distance from the population is greater than a

given level ∆. When ∆ equals 0, it simply consists in

eliminating copies. The management procedure starts

by sorting the chromosomes of a population P in a

decreasing order of their quality, which corresponds

to increasing order of costs. The population size is

constant, that means when a new solution is accepted,

another solution is eliminated. To maintain the best

found solutions, the solution to be eliminated is se-

lected randomly in the worst half of the population.

The level ∆ is then updated based on the rate of re-

fusal or acceptance of solutions (when more than M

solutions are accepted, ∆ is increased by one unit,

and when more than M solutions are rejected, ∆ is

decreased by one unit).

MemeticAlgorithmwithPopulationManagementfortheTwo-dimensionalLoadingVehicleRoutingProblemwithPartial

Conflicts

191

3.5 Modiﬁed Shelf Heuristic

Fill-Dynamic (SHF-D)

This heuristic was introduced by Ben Messaoud et al.

(BenMessaoud et al., 2004) and is mainly used for

guillotine cutting problems. In this kind of problems,

the cutting tool has to go from one edge of the rectan-

gle (or the strip to cut) to the other. Shelf algorithms

allow to resolve this problem. Packing is obtained by

inserting items from the left to the right side, while

forming shelfs. The ﬁrst shelf corresponds to the rect-

angle bottom. The next shelf bottom is obtained with

the horizontal line that coincide with the top of the

highest item in the previous shelf. The treatment is re-

peated for all items. The modiﬁed version presented

in this section was proposed for the 2BPPC by Dhaoui

et al. (Dhaoui et al., 2012).

In the classical version, items are sorted out in

a decreasing order of heights. In this modiﬁed ver-

sion, items are separated into sets corresponding to

their classes (as in hazardous materials classiﬁcation,

items are assigned to classes and the partial conﬂicts

are rather deﬁned between classes than items). Then

they are inserted in a way that the items of two classes

treated successively are not conﬂicting. If it is im-

possible to obtain an order that separates every pair

of conﬂicting classes, a safety distance is kept when

necessary.

The procedure that sorts out the classes starts by

assigning the ﬁrst position to the class that has the

biggest degree of conﬂicts. The degree of conﬂicts of

a class corresponds to the number of classes conﬂict-

ing with it. After adding a class to the list, the follow-

ing class is chosen among the classes non conﬂicting

with it.

The procedure sorting out the classes is described

in Algorithm 1. Classes stands for the table of classes

and represents the input of the algorithm, while List

is the output corresponding to the new order of the

classes. Nc is the number of classes and c and ind

are indexes of the classes. Degree is a table in which

are recorded the degree of the classes. Finally, Com-

patible is a boolean that takes the value true if the

considered classes are compatible, and the value false

if not.

Each item is inserted in the lowest possible po-

sition left-justiﬁed in the ﬁrst shelf where it ﬁts en-

tirely, if any. If none of the existing shelfs can contain

it, a new shelf is initialized. This heuristic is differ-

ent from other classical shelf algorithms with its ten-

dency to reuse at best the free areas in each shelf, by

inserting items on top of the others while preserving

guillotine cutting constraints.

At any stage of the heuristic, each used bin con-

Algorithm 1: Sorting out classes Procedure.

Sort out Classes in a decreasing order of Degree

c = 1

List(c) = Classes(c)

Repeat

ind = c + 1

Compatible = false

Repeat

If (Classes(ind) conﬂicts with List(c)) then

ind = ind + 1

Else Compatible = true

Until ((Compatible = true) or (ind = Nc))

If (Compatible = true) then List(c) =

Classes(ind)

Else List(c) = Classes(c+1)

c = c + 1

Until (c = Nc)

tains a set of empty spaces. These spaces are available

rectangles; each of them is deﬁned with its height,

width and coordinates of its bottom left corner. To

place an item, the method proceeds by examining

each available rectangle in turn and ﬁnding whether

the item ﬁts into it and whether it is conﬂicting with

the already packed items that surround the considered

rectangle. Rectangles are examined in an increasing

order of the ordinates of their bottom left corner. In

case of equality, abscissa is considered and the rect-

angle with lowest value of abscissa is examined ﬁrst.

In Figure 3, after the insertion of item 1, the used

available rectangle is deleted while two new available

rectangles are created: Top (W

= W, H

= H − y

) is

the available rectangle on top of the inserted item and

Right (W

= W − x

, H

= H) is the available rectan-

gle on its right.

Figure 3: Available rectangles.

The procedure Update is described in Algorithm

2. Nr is the number of available rectangles. Let p be

the index of the available rectangle where the current

item is inserted. If there is an intersection between

an existing rectangle r and the rectangle p, the di-

mensions of the rectangle r are modiﬁed in order to

eliminate the intersection area. If the new height or

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

192

width of the treated rectangle becomes null, the rect-

angle is deleted. Two new rectangles are created (Top

and right) and the rectangle p is deleted.

Algorithm 2: Procedure to update available rectangles.

Create Rectangles (Top) and (Right)

For r = 1 to Nr

If Rectangle(r) ∩ Rectangle(p) 6=

Update Rectangle(r)

If (W

= 0 or H

= 0) Delete Rectangle(r)

end for

Delete Rectangle(p)

Sort out Rectangle

In the dynamic version of the method (SHF-D), a

shelf height is not ﬁxed with the height of the ﬁrst in-

serted item. A temporary height is updated after each

insertion. Let Nr be the number of available rectan-

gles in the current bin and Ns the number of shelfs

within it. If the current item does not ﬁt in all the

Nr − 1 available rectangles and the last rectangle has

to be used (the rectangle with the biggest ordinate of

bottom-left corner), a new shelf is initialized with this

item and the height of the previous shelf is ﬁxed. In

Algorithm 3, let p be the index of the valid rectangle

and Y

its ordinate.

Algorithm 3: Fix shelf height Procedure.

If (p = Nr) then

Shelf Height(Ns) = Y

Ns = Ns + 1

Initialize Shelf(Ns) with Current Item

else

Insert Current Item in Shelf(Ns)

End if

3.6 Local Search

Three kinds of moves are used, each of them deﬁning

a neighborhood structure. For the moves that concern

two different routes, the packing feasibility is checked

with modiﬁed SHF-D and only feasible moves are

performed. The moves are sorted in increasing order

of complexity and are:

Move 1: Customer Relocation

This move type relocates a customer from his current

position to another position. The move can be used

for every possible insertion position, and can involve

only one route or two different routes.

Move 2: Position Exchange

This move type exchanges the routes that cover a

pair of customers. The two customers swap their po-

sitions in the routes too. It is employed for every

pair of routes and for every customer pair involved in

the considered routes. When the move is performed

within a single route, the customers swap their posi-

tions within this route.

Move 3: 2-opt

The move 2-opt is deﬁned by two customers a and

b. Let X be a route represented as a list of customers

containing a copy of the depot in the beginning and

at the end, X = (x

= 0, x

, ..., x

, x

t+1

= 0). Only the

case where a and b are within the same route X with

= a, x

= b and i ≤ j is considered. The move 2-opt

consists in inverting the subsequence (x

, x

i+1

, ..., x

It is replaced by the subsequence (x

, x

j−1

, ..., x

4 EXPERIMENTAL RESULTS

The used computer is a PC Pentium(R) Dual-Core

CPU T4400 2.20 GHz with an operating system Win-

dows 7. For our tests, we adapted the instances of

Iori (Iori, 2004) created for the 2L-CVRP. In these

instances, the number of items and their sizes are cre-

ated in ﬁve sets. The ﬁrst set corresponds to instances

of a capacitated vehicle routing problem (CVRP). In

the set i, with i = 1, ..., 5, the number of items assigned

to each customer ranges from 1 to i. Dimensions of

items are generated according to uniform distribution

in given intervals (Iori et al., 2007). In these instances

the number of customers ranges from 15 to 35, while

the number of items is between 15 and 114.

In order to obtain 2LPC-CVRP instances, each

item is assigned to one of 5 categories of hazardous

materials and a class index is then associated ran-

domly to each item. Partial conﬂicts are generated

randomly between some classes. The obtained in-

stances are constituted of 16 groups of instances, each

one contains ﬁve ﬁles.

For the main parameters setting, a design of exper-

iments ”Latin Square” with 9 situations and 3 levels

was used. The parameters are ﬁxed as follows: (NG,

NP, α) = (20, 20, 1), where NG is the number of gen-

erations, NP is the population size and α is the rate of

local search.

The results on the instances considering the con-

ﬂicts into account are given in the table 1. The aim is

to minimize the overall traveling cost (as in the clas-

sical CVRP) when assuming an unlimited number of

vehicles. The obtained total cost and the computing

time are reported.

The algorithm was also tested on the instances

without conﬂicts in order to estimate its performance

when compared to the best results of the literature ob-

MemeticAlgorithmwithPopulationManagementfortheTwo-dimensionalLoadingVehicleRoutingProblemwithPartial

Conflicts

193

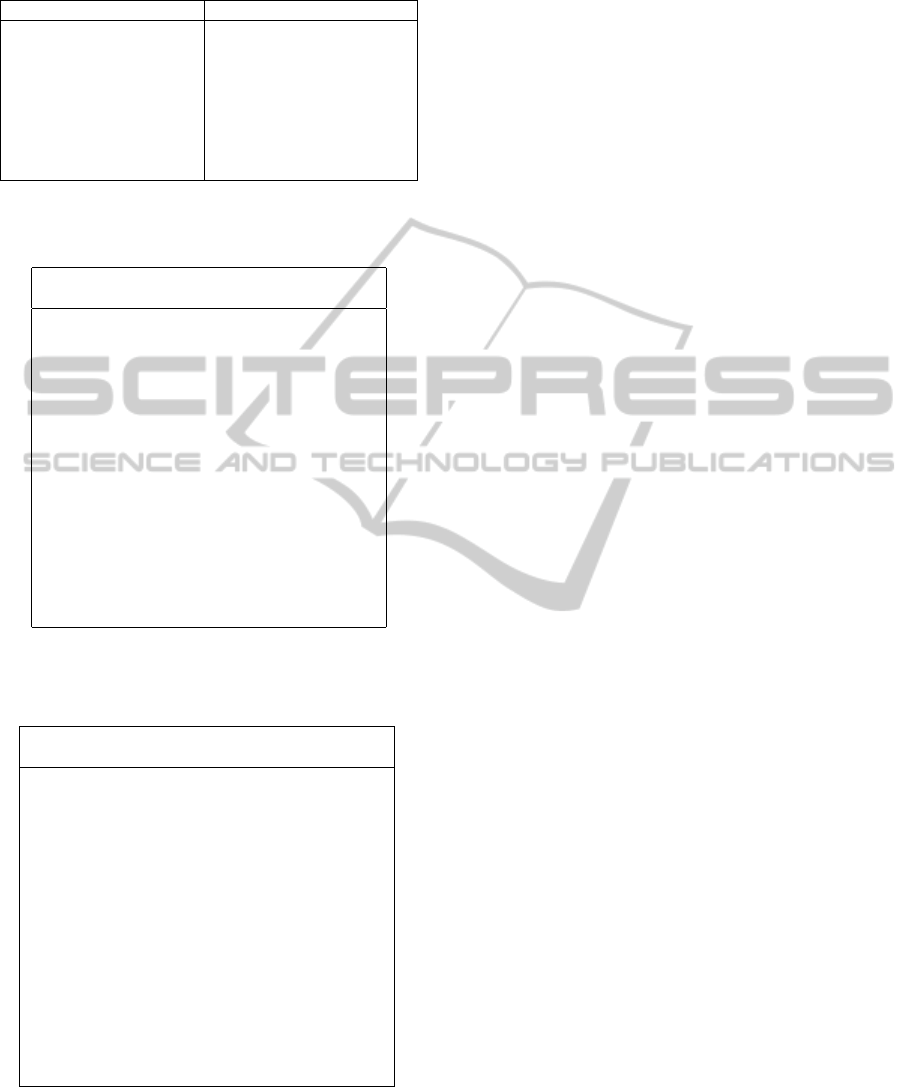
Table 1: Average results of our MA per group of instances.

Group Cost Time Group Cost Time

1 327,85 1,61 9 677,97 4,32

2 370,89 2,80 10 725,66 5,12

3 427,45 1,84 11 683,89 3,84

4 403,49 4,12 12 2232,56 5,66

5 483,41 3,94 13 1593,85 5,78

6 643,60 3,50 14 1308,52 7,14

7 687,91 3,92 15 851,64 4,96

8 848,06 4,10 16 708,10 3,50

Table 2: Average results for set 1 (CVRP) of Iori instances

(groups from 1 to 16).

Groups Best MA

Cost Time Cost Time

1 278,73 0,11 278,73 3,1

2 334,96 0,02 334,96 0,04

3 358,85 0,69 358,85 2,8

4 430,88 0,83 430,88 2,1

5 375,28 0,13 375,28 3,4

6 485,85 0,66 495,85 1.3

7 568,56 0,25 568,56 4

8 568,56 0,19 568,56 3,5

9 607,65 3,97 607,65 4,7

10 535,8 0,59 558,27 4,1

11 505,01 0,8 531,30 4,2

12 610.00 12,6 646,46 3,6

13 2006,3 0,83 2248,21 4,4

14 837,67 0,74 913,18 4,1

15 837,67 1,36 1136,70 2,3

16 698,61 22,8 708,42 4,3

Table 3: Average results for sets from 2 to 5 (2L-CVRP) of

Iori instances (groups from 1 to 16).

Groups Best MA

Cost Time Cost Time

1 284,42 0,90 286,89 1,3

2 339,26 0,10 339,26 1,40

3 376,32 0,50 381,34 2,5

4 435,01 0,20 443,25 1,1

5 379,04 0,10 401,01 5,00

6 497,04 0,40 506,13 4,00

7 691,11 1,40 720,79 3,8

8 678,84 0,80 747,32 3,9

9 612,01 0,60 625,50 1,9

10 675,79 15,10 744,65 5,6

11 705,95 11,30 771,83 5,6

12 611,26 16,90 663,18 4,3

13 2490,62 78,00 2859,10 5,9

14 984,42 79,90 1199,27 7,1

15 1144,69 257,70 1275,25 7,7

16 699,79 6,00 709,75 5,1

tained by Duhamel et al. (Duhamel et al., 2011). For

this purpose, a restriction on the number of vehicles

is added. We consider non-sequential packing with-

out items rotation. In average, our MA has a distance

of 6% from the best known solutions.

In Table 2, the results on the ﬁrst group of in-

stances are reported. this group corresponds to a pure

transportation problem. Our algorithm ﬁnds the best

known solutions for 8 out of 16 instances. The com-

putation time of our MA does not exceed 5 seconds,

while it may be much higher for some results obtained

by Duhamel et al. (Duhamel et al., 2011).

Table 3 gives the average results for sets from 2 to

5. Our algorithm ﬁnds the best known average only

for set 2. For the other sets, our results are very close

to the best known results in the literature, particularly

for instances of the ﬁrst groups (groups 1 to 6). For

8 groups out of 16, the gap is less than 4%. For 7

other groups the gap ranges from 6% to 14%. Only

the gap of the group 14 is over 20%. The average gap

obtained for all studied instances to the best known

solutions is about 6.6%.

5 CONCLUSIONS

This paper presents a ﬁrst study for the two-

dimensional loading with partial conﬂicts capacitated

vehicle routing problem. A memetic algorithm with

population management is designed to solve routing

part, while a heuristics is used to solve packing prob-

lem. The ﬁrst results are promising. Further results

would be given in the conference.

REFERENCES

Beaumont, O., Bonichon, N., and Larchev

eque, H. (2010).

Bin packing under distance constraint. Technical re-

port, Universit

e de Bordeaux, Laboratoire Bordelais

de Recherche en Informatique, INRIA Bordeaux Sud-

Ouest.

BenMessaoud, S., Chu, C., and Espinouse, M. (2004). An

approach to solve cutting stock sheets. Scottish Math-

ematical Council, 6:5109–5113.

Clarke, G. and Wright, J. (1964). Scheduling of vehicles

from a central depot to a number of delivery points.

Operations Research, 12:568–581.

Dhaoui, K., Labadie, N., and Yalaoui, A. (2012). Algo-

rithms for the two dimensional bin packing problem

with partial conﬂicts. RAIRO - Operations Reseach,

accepted.

Duhamel, C., Lacomme, P., Quilliot, A., and Toussaint,

H. (2011). A multi-start evolutionary local search

for the two dimensional loading capacitated vehicle

routing problem. Computers & Operations Research,

38(3):617–640.

Environment Canada (2002). Compliance promotion bul-

letin (compro no. 12) - regulations for the manage-

ment of hazardous waste.

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

194

Fuellerer, G., Doerner, K., Hartl, R., and Iori, M. (2009).

Ant colony optimization for the two-dimensional

loading vehicle routing. Computer & Operations Re-

search, 36(3):655–673.

Gendreau, M., Iori, M., Laporte, G., and Martello, S.

(2008). A tabu search heuristic for the vehicle routing

problem with two-dimensional loading constraints.

Networks - Special Issue In Memory of Stefano Pal-

lottino, 51:4–18.

Goldberg, D. (1989). Genetic Algorithms in Search, Op-

timization and Machine Learning. Addison-Wesley,

Reading, Massachussett, USA.

Iori, M. (2004). Metaheuristic algorithms for combinato-

rial optimization problems. PhD thesis, University of

Bologna, Italy.

Iori, M., Salazar-Gonzalez, J. J., and Vigo, D. (2007). An

exact approach for vehicle routing problem with two-

dimensional loading constraints. Transportation Sci-

ence, 41(2):253–264.

Khebbache, S., Prins, C., Yalaoui, A., and Reghioui, M.

(2011). Heuristics and memetic algorithm for the two-

dimensional loading capacitated vehicle routing prob-

lem with time windows. Central European Journal

of Operations Research, pages DOI: 10.1007/s10100–

011–0204–9.

Leung, S., Zhou, X., Zhang, D., and Zheng, J. (2011). Ex-

tended guided tabu search and a new packing algo-

rithm for the two-dimensional loading vehicle rout-

ing problem. Computers & Operations Research,

38(1):205–215.

Mart

ı, R., Laguna, M., and Campos, V. (2005). Scatter

search vs genetic algorithms: an experimental eval-

uation with permutation problems. Metaheuristic Op-

timization via Memory and Evolution: Tabu Search

and Scatter Search, Boston, Kluwer. C. Rego and B.

Alidaee, editors.

Moura, A. (2008). A multi-objective genetic algorithm for

the vehicle routing with time windows and loading

problem. Intelligent Decision Support, pages 187–

201.

Moura, A. and Oliveira, J. F. (2009). An integrated ap-

proach to the vehicle routing and container loading

problems. Operations Research Spectrum, 31(4):775–

800.

Prins, C. (2004). A simple and effective evolutionary algo-

rithm for the vehicle routing problem. Computers and

Operations Research, 31:1985–2002.

orensen, K. and Sevaux, M. (2006). MA|PM: Memetic

algorithms with population management. Computers

and Operations Research, 33(5):1214–1225.

Stoyan, Y. and Chugay, A. (2009). Packing cylinders and

rectangular parallelepipeds with distances between

them into a given region. European Journal of Op-

erational Research, 360(197):446–455.

Stoyan, Y. G. and Yaskov, G. N. (1998). Mathematical

model and solution method of optimization problem

of placement of rectangles and circles taking account

special constraints. International Transactions on Op-

erational Research, 5(1):45–57.

Zachariadis, E., Tarantilis, C., and Kiranoudis, C. (2009).

A guided tabu search for the vehicle routing problem

with two-dimensional loading constraints. European

Journal of Operational Research, 195(3):729–743.

MemeticAlgorithmwithPopulationManagementfortheTwo-dimensionalLoadingVehicleRoutingProblemwithPartial

Conflicts

195