
Evolving Art using Measures for Symmetry, Compositional Balance
and Liveliness
Eelco den Heijer
Department of Computer Science, Vrije Universiteit, Amsterdam, Netherlands
Objectivation B.V., Amsterdam, Netherlands
Keywords:
Evolutionary Art, Aesthetic Measures, Computational Aesthetics, Symmetry, Compositional Balance.
Abstract:
In this paper we present our research into the unsupervised evolution of aesthetically pleasing images using
measures for symmetry, compositional balance and liveliness. We evolve images without human aesthetic
evaluation, and use measures for symmetry, compositional balance and liveliness as fitness functions. Our
symmetry measure calculates the difference in intensity of opposing pixels around one or more axes. Our
measure of compositional balance calculates the similarity between two parts of an image using a color image
distance function. Using the latter measure, we are able to evolve images that show a notion of ‘balance’ but
are not necessarily symmetrical. Our measure for liveliness uses the entropy of the intensity of the pixels of
the image. We performed a number of experiments in which we evolved aesthetically pleasing images using
the aesthetic measures, in order to evaluate the effect of each fitness function on the resulting images. We
also performed an experiment using a combination of aesthetic measures using a multi-objective evolutionary
algorithm (NSGA-II).
1 INTRODUCTION
Symmetry is ubiquitous in everyday life; human be-
ings show bilateral (or vertical) symmetry in the build
of their bodies and faces and objects like cars, houses,
gadgets, etc. often show a reasonable degree of sym-
metry. Although most people have a notion of the
concept of symmetry, it is a concept with multiple
meanings. First of all, there is reflectional symmetry;
this is probably the most popular use of the notion of
symmetry. It refers to the property that one half of
an image is the reflection of the other part of the im-
age; one half is mirrored around an axis onto the other
half. When using a vertical axis, this form of symme-
try is known as bilateral symmetry, left/ right symme-
try, mirror symmetry or horizontal symmetry. Bilat-
eral symmetry is prevalent in design, architecture and
nature; it occurs in the design of cathedrals and other
buildings, cars, vases, but also in the human body and
in most animal bodies. In the remainder of this paper,
we will refer to these types of symmetry as bilateral
symmetry (vertical axis), top-down symmetry (hori-
zontal axis) and diagonal symmetry (diagonal axis).
Besides the aforementioned forms of symmetry, there
are several other forms of symmetry, like rotational
symmetry (symmetry around a point), translational
symmetry, radial symmetry, etc. These forms of sym-
metry are all outside the scope of this paper.
A second meaning of symmetry is the notion of
balance of proportion, or self-similarity (Weyl, 1983).
This notion of symmetry is less ‘strict’, less well-
defined than bilateral symmetry. An image is visually
balanced if an observer perceives two parts, divided
by an axis (not necessarily in the centre of the im-
age), whereby the two parts have the same ‘weight’
(Arnheim, 1988). The notion of weight in this con-
text is not clearly defined; in some cases a number
of small items on one side of the image can have the
same weight as one larger object on the other side of
the image. Or, a large group of bright items on one
side of the image may have the same weight as a small
group of darker items on the other side of the image.
In the domain of design, the notion of (vertical) bal-
ance is an important factor. White defines symmetric
balance as ‘vertically centered, and equivalent on both
sides’ (White, 2011). This raises the question; when
are two sides ‘equivalent’? The notion of balance is
used more frequently in design and the visual arts than
the use of strict symmetry (the strict use of symmetry
in paintings is quite rare). However, the notion of bal-
ance is not well defined, which makes it challenging
to formalise in an aesthetic measure. Since the no-
52
den Heijer E..
Evolving Art using Measures for Symmetry, Compositional Balance and Liveliness.
DOI: 10.5220/0004149600520061
In Proceedings of the 4th International Joint Conference on Computational Intelligence (ECTA-2012), pages 52-61
ISBN: 978-989-8565-33-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

tion of balance is difficult to formalise, and since we
evolve mainly abstract images without composition
or distinct representational elements (which makes it
even more difficult to calculate ‘balance’), we decided
to develop an aesthetic measure based on composi-
tional balance (which is related to balance, but not
the same); we calculate image feature vectors for two
parts of an image and calculate the difference between
these vectors (see Section 3).
Symmetry has often been associated with aesthe-
tic preference, although its exact relation remains un-
clear. The human visual system is very well equipped
to perceive symmetry in an image; humans can detect
whether an image is symmetric within 100ms, which
suggests that the perception of symmetry is ‘hard-
wired’ in the visual perceptive system (Locher and
Nodine, 1989). According to Reber et al aesthetic
experience of a visual stimulus is linked to the pro-
cessing fluency of that stimulus (Reber et al., 2004).
The more fluently an observer can process a stimulus,
the more positive is the aesthetic response. One of
the key variables that Reber et al determine is sym-
metry. Bauerly and Liu showed symmetric images
and asymmetric images of web pages to test persons
and measured the aesthetic response (Bauerly and
Liu, 2005, Bauerly and Liu, 2008). They found that
symmetry correlates positively with aesthetic prefer-
ence (of web pages) and bilateral symmetry correlates
higher with aesthetic preference than top-down sym-
metry. Aesthetic preference also correlates with bi-
lateral symmetry in the perception of human faces.
Symmetry is one of the most salient features that mark
personal attractiveness; but symmetry is more a nec-
essary pre-condition than a guarantee for attractive-
ness; the absence of symmetry (asymmetry) in the
human body (especially in the face) severely reduces
personal attractiveness (Dutton, 2009, Etcoff, 1999).
Aesthetic preference in art is less straightfor-
ward. In general, strict symmetric paintings are rare,
and usually considered boring (Locher and Nodine,
1989). In the visual arts, symmetry is often used on a
higher level, often in balancing elements of the com-
position (Locher and Nodine, 1989). Locher et al re-
fer to this notion as ‘dynamic symmetry’, others refer
to this as ‘balance’. We used an abstract version of
‘dynamic symmetry’ and balance, and in the remain-
der of this paper we shall refer to this notion as com-
positional balance.
The development of the aesthetic measures is
driven by our research in unsupervised evolutionary
art. In previous work we investigated the applica-
bility of Multi-Objective Evolutionary Algorithms to
evolve art using multiple aesthetic measures (den Hei-
jer and Eiben, 2011). One of the main conclusions
of that work was that MOEA is suitable for unsuper-
vised evolutionary art, but only if the aesthetic mea-
sures cooperate; we performed experiments with a
number of combinations of two aesthetic measures,
and found that some combinations work very well,
and some combinations produced disappointing re-
sults. We concluded that it is very important to use a
‘right’ combination of aesthetic measures, preferably
a combination of aesthetic measures that work on dif-
ferent aspects or ‘dimensions’ of an image. In this pa-
per we want to add aesthetic measures that act on two
aspects, dimensions that have not yet been explored
in unsupervised evolutionary art; symmetry and com-
positional balance.
Our research questions are
1. is it possible to evolve interesting symmetric aes-
thetically pleasing images using a measure for
symmetry? (and is it possible to control the
amount of symmetry in the images?)
2. is it possible to evolve interesting ‘balanced’ aes-
thetically pleasing images using a measure for
compositional balance?
3. can the measures of symmetry and composi-
tional balance be combined successfully with
other (existing) aesthetic measures to evolve aes-
thetically pleasing images; we define the combi-
nation as ‘successful’ if the resulting images are
aesthetically pleasing or interesting, and prefer-
ably ‘new’, i.e. the style of the images should be
different from images from previous experiments.
The rest of the paper is structured as follows. First
we discuss related work in Section 2, next we present
our aesthetic measures for symmetry, compositional
balance and liveliness in Section 3. We shortly de-
scribe our evolutionary art system in Section 4. Next
we describe our experiments and their results with our
aesthetic measures in single and multi-objective evo-
lutionary algorithm (MOEA) setups in Section 5. We
finish our paper with conclusions and directions for
future work in Section 6.
2 RELATED WORK
The use of methods and techniques from the field
of computational aesthetics in evolutionary art is rel-
atively new. The first attempt to evolve art in an
unsupervised manner was described by Baluja et al
(Baluja et al., 1994). Baluja et al built an unsuper-
vised evolutionary art system, and constructed a neu-
ral network to perform the aesthetic evaluation. The
authors concluded that the results were ‘not satis-
factory’. Since Baluja et al a number of other au-
EvolvingArtusingMeasuresforSymmetry,CompositionalBalanceandLiveliness
53

thors have developed unsupervised evolutionary art
systems (Machado and Cardoso, 2002, Ross et al.,
2006). The aesthetic measure described in (Machado
and Cardoso, 1998) builds on the relation between
Image Complexity (IC) and Processing Complexity
(PC). Images that are visually complex, but are pro-
cessed easily have the highest aesthetic value. As
an example, the authors refer to fractal images; they
are visually complex, but can be described by a rela-
tively simple formula. The aesthetic measure by Ross
& Ralph is based on the observation that many fine
art painting exhibit functions over colour gradients
that conform to a normal or bell curve distribution.
The authors suggest that works of art should have a
reasonable amount of changes in colour, but that the
changes in color should reflect a normal distribution
(Ross et al., 2006). The Global Contrast Factor is
an aesthetic measure that computes contrast (differ-
ence in luminance) at various resolutions. Images that
have little or few differences in luminance have low
contrast and are considered ‘boring’, and thus have a
low aesthetic value. Contrast is computed by calcu-
lating the (average) difference in luminance between
two neighbouring super-pixels. Super-pixels are rect-
angular blocks in the image. The contrast is calcu-
lated for several resolutions (2, 4, 8, 16, 25, 50, 100
and 200). For more details on the Global Contrast
Factor we refer to the original paper (Matkovic et al.,
2005). We have implemented the Global Contrast
Factor and will use it in combination with one of our
aesthetic measures in our experiment using the Non-
dominating Sorting Genetic Algorithm II (or NSGA-
II) (see Section 5.3).
In the field of Human-Computer Interaction re-
search has been done on the automatic evaluation of
web pages. Ngo et al have developed a number of
aesthetic measures to evaluate screen design (Ling
et al., 2000) and symmetry and balance are two of
the measures. The authors define symmetry as the
balanced distribution of equivalent (screen) elements
around a common line; they divide the screen in four
quadrants, assign a weight to each quadrant based
on the content of the quadrant, and define symme-
try as the summed difference between the quadrant
weights. Bauerly and Liu have developed a metric
for symmetry to measure symmetry in a design con-
text (with an emphasis on web pages) (Bauerly and
Liu, 2005, Bauerly and Liu, 2008). Their metric cal-
culates how often two pixels at the two sides of an
axis have the same value (Bauerly and Liu use bi-
nary values for pixels; black and white). The com-
parison between two pixels is multiplied by a weight
factor that depends on the distance of the pixels to the
axis; if a pixel is close to the axis, it will result in a
higher weight. Our aesthetic measure for symmetry
is similar to the one by Bauer and Liu, but there are
a few differences; we calculate the intensity value of
the pixels (256 possible values), and Bauer and Liu
convert the image to a binary image (a pixel is ei-
ther black or white). Furthermore, we do not take the
distance of the pixel to the axis into account. The
aesthetic measure for ’balance’ by Ngo et al (Ling
et al., 2000) is not applicable in our context; Ngo
et al used their aesthetic measures on user interfaces
and web pages, which have distinct compositional el-
ements. Our evolutionary art system evolves abstract
images that have no distinct compositional elements,
although one could argue that some images show dis-
tinct (non-representational) objects. This is the main
reason we chose to design and implement an aesthetic
measure that calculates compositional balance.
3 AESTHETIC MEASURES FOR
SYMMETRY,
COMPOSITIONAL BALANCE
AND LIVELINESS
In this section we describe our aesthetic measures for
symmetry, compositional balance and liveliness.
3.1 Calculating Symmetry
We have designed and implemented an aesthetic mea-
sure that computes the reflectional symmetry of an
image. The calculation of symmetry is done as fol-
lows. First, we divide the image in four quarters,
cutting the image in half across the horizontal and
vertical axis (areas A
1
, A
2
, A
3
, A
4
), see figure 1).
Left, right, top, and bottom areas are defined as
Figure 1: For the symmetry aesthetic measure we divide the
area in four quadrants.
A
le ft
= A
1
+ A
3
, A
right
= A
2
+ A
4
, A
top
= A
1
+ A
2
and
A
bottom
= A
3
+A
4
. The horizontal reflectional symme-
try of an image I is defined as the similarity between
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
54

its two area halves A
le ft
and A
right
;
S
h
(I) = s(A
le ft
, A
right
) (1)
and the vertical similarity is calculated as
S
v
(I) = s(A
top
, A
bottom
) (2)
and diagonal symmetry is defined as
S
d
(I) =
s(A
1
, A
4
) + s(A
2
, A
3
)
2
(3)
The similarity between two areas s(A
1
, A
2
) is defined
as
s(A
i
, A
j
) =
∑
w
x=0
∑
h
y=0
(sim(A
i
(x, y),A
m
j
(x, y))
w · h
(4)
where x and y are the coordinates of the pixel, w and y
are the width and height of the area (they are the same
for all the areas in the calculations), and A
m
j
is the mir-
rored area of A
j
; for horizontal symmetry we mirror
A
j
around the vertical axis, for vertical symmetry we
mirror A
j
around the horizontal axis, and for diago-
nal symmetry we mirror A
j
around both axes. Next,
we define the similarity between two opposing pixels
sim(A
i
(x, y),A
j
(x, y)) as
sim(A
i
(x, y),A
j
(x, y)) =
1 if |I(A
i
(x, y))−
I(A
m
j
(x, y))| < α,
0 otherwise
(5)
where I(A
i
(x, y)) refers to the intensity value of a
pixel (x, y) in area A
i
, and α is a difference thresh-
old. We tried a number of settings for α and chose
α = 0.05 as a setting in our experiments (where
I(x, y) ∈ [0..1]). The intensity of a 24 bit RGB pixel
I(x, y) is defined as the average of its red, green and
blue value;
I(x, y) =
r(x, y) + g(x, y) + b(x, y)
3
(6)
Note that intensity is not the same as brightness;
brightness refers to the perceived lightness, and uses
different weights for the (r, g, b) components (in fu-
ture work we intend to experiment with brightness
and luminosity instead of intensity). We define the
aesthetic measure for (strict) symmetry as
AM
sym1
(I) = S
m
(I) (7)
where m is horizontal, vertical or diagonal. For com-
binations, we calculate the average of the distinct
symmetries. For example, for combined horizontal,
vertical and diagonal symmetry (useful for evolving
tiling patterns, wallpaper etc.), we calculate the aes-
thetic value as
AM
sym1
(I) =
S
h
(I) + S
v
(I) + S
d
(I)
3
(8)
As mentioned earlier in Section 1, the relation be-
tween symmetry and aesthetic preference is not well
defined; several publications suggest that a certain
amount of symmetry in visual arts is appreciated, but
(especially in Western art) many people consider too
much symmetry or ‘complete’ symmetry (or ‘static’
symmetry) to be boring. This is consistent with the
processing fluency theory by Reber et al (Reber et al.,
2004); if there is too much symmetry in an image,
many people will process the image ‘too fluently’
since the complexity of the image is below a cer-
tain threshold. In other words; images with too much
symmetry are often considered as simple and boring.
With this observation in mind, we created an alterna-
tive version of our first measure, that rewards images
highest if they have a symmetry value of T , where T
is our ‘optimal amount of symmetry’. We did not find
a proper value in literature for this ‘optimal amount’
of symmetry, so we tried a number of settings and
found that a value of 0.8 resulted in images with am
‘agreeable’ amount of symmetry (although we did not
verify this on a group of test persons). In our adapted
version of the bilateral symmetry measure we calcu-
late the actual symmetry value of an image using the
first symmetry measure, and multiply this with a gaus-
sian function with b = 0.8 (this is our chosen ‘optimal
amount’ of symmetry) and c = 0.2 (the c variable in
a gaussian determines the width of the bell curve, and
after a number of trial experiments we decided to use
c = 0.2);
AM
sym2
(I) = e
−
(x−T )
2
2c
2
= e
−
(AM
sym1
(I)−0.8)
2
0.08
(9)
The effect of this gaussian function is that this alter-
native or ‘relaxed’ measure of symmetry rewards im-
ages highest (score 1.0) if the amount of symmetry
is 0.8. Images with a higher symmetry value (higher
than 0.8) score lower; see Figure 2.
3.2 Calculating Compositional Balance
We implemented a measure that calculates the hori-
zontal (or left-right) compositional balance of an im-
age. Our measure use the Stricker & Orengo image
distance function (Stricker and Orengo, 1995). This
distance function d
so
computes the distance between
two images I
a
and I
b
by calculating the distance be-
tween the two image feature vectors v
a
and v
b
, where
d
so
(I
a
, I
b
) =
∑
i<N
i=0
w
i
· |v
a
i
− v
b
i
|
∑
i<N
i=0
w
i
(10)
where N is the number of image features (in our im-
plementation N = 12, see Table 1 for the 12 image
EvolvingArtusingMeasuresforSymmetry,CompositionalBalanceandLiveliness
55
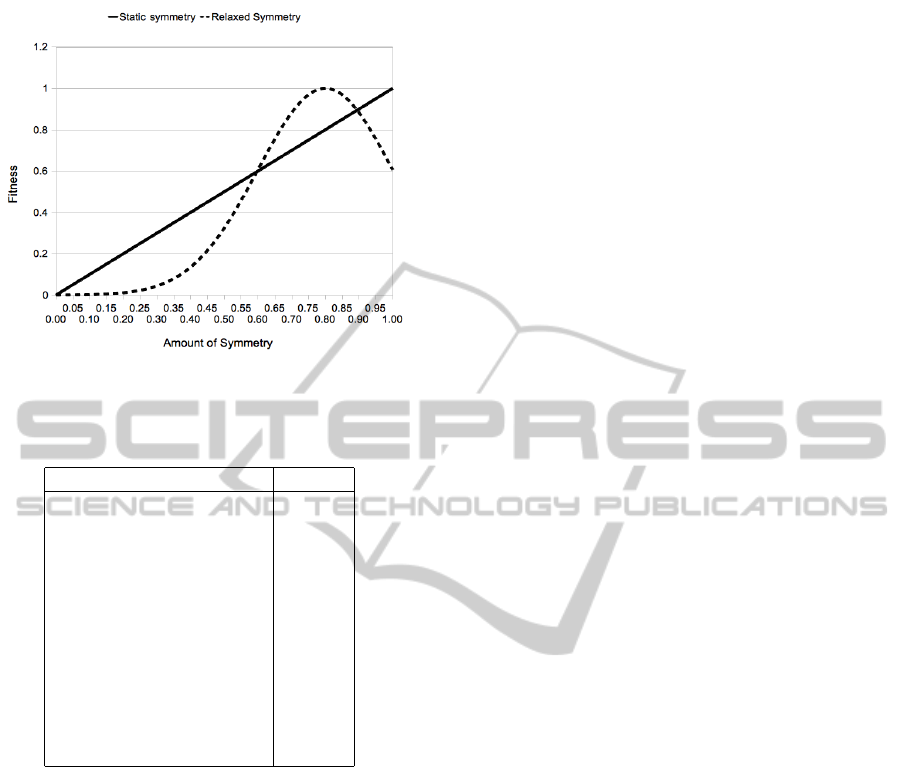
Figure 2: The relation between the amount of symmetry and
fitness for our two symmetry aesthetic measures.
Table 1: Image features and their weights used in our
Stricker & Orengo image distance function.
Image feature Weight
Hue (avg) 4
Hue (sd) 4
Hue (skewness) 4
Saturation (avg) 1
Saturation (sd) 1
Saturation (skewness) 1
Intensity (avg) 2
Intensity (sd) 2
Intensity (skewness) 2
Colourfulness (avg) 2
Colourfulness (sd) 2
Colourfulness (skewness) 2
features). For the image features we used the average,
standard deviation and skewness of the hue, satura-
tion, intensity and colourfulness of the colour pixels
of the image (in the HSV colour space). Each im-
age feature is assigned a weight w and the weights are
shown in Table 1.
The amount of compositional balance of an image
is calculated as
M
cb
(I) = 1 − d
so
(I
le f t
, I
right
) (11)
Although we calculate only the horizontal or left-right
compositional balance of an image, it should be triv-
ial to extend this measure to calculate top-down and
diagonal compositional balance (similar to our calcu-
lations of symmetry in Section 3.1).
3.3 Calculating ‘Liveliness’ using
Entropy
If we merely use a measure of symmetry as a fit-
ness function to evolve images, we would end up with
many monotonous, maybe even monochrome images.
A monotonous image is relatively easy to evolve and
often has a lot of left-right symmetry, and conse-
quently will score high on our fitness function. In or-
der to evolve ‘interesting’ symmetric images, we also
need to incorporate a calculation of ‘interestingness’,
or ‘liveliness’ of an image, and incorporate this no-
tion into the calculation of the fitness function. There
has been prior research into the calculation of com-
plexity of images; Machado and Cardoso use jpeg
compression and wavelet compression to calculate
the image complexity and processing complexity with
which they construct an aesthetic measure to evolve
images without human evaluation (Machado and Car-
doso, 1998, Machado and Cardoso, 2002). From our
own observations we have seen that images that are
interesting or lively often exhibit variation in inten-
sity across the image. With this observation in mind
we have developed a simple measure that calculates
the entropy of the intensity of the pixels of the image
(analogous to the work by Rigau et al (Rigau et al.,
2008)). Images that are very monotonous will little
variation in the intensity of the pixels and will have
low entropy, and images with a lot of different inten-
sity values will have high entropy. We calculate the
entropy for all possible intensity values, and since we
use 24 bit RGB images, we have 256 different inten-
sity values. The We define ‘liveliness’ as
M
liveliness
(I) = −
n
∑
i=1
p(x
i
)log(p(x
i
)) (12)
where x
i
∈ [0, .., 255] refers to the intensity of the pix-
els, and p(x
i
) refers to the probability of the intensity
value x
i
.
3.4 Summary of our Aesthetic Measures
With the measure of symmetry and the measure of
liveliness we construct our aesthetic measure for sym-
metry as follows;
AM
∗
sym1
(I) = AM
sym1
(I) · M
liveliness
(I) (13)
and our measure of ‘relaxed’ symmetry is defined as
AM
∗
sym2
(I) = AM
sym2
(I) · M
liveliness
(I) (14)
and our aesthetic measure for compositional balance
is defined as
AM
cb
(I) = M
cb
(I) · M
liveliness
(I) (15)
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
56

Although we use two measures to calculate a single
score, it’s not the same as multi-objective optimisa-
tion (MOO). In MOO the two scores would be stored
and optimised separately, and in our aesthetic mea-
sures we only use the product of the two separate mea-
sures.
In our first three experiments we will use the aes-
thetic measures defined in Equation 13, 14, 15 respec-
tively.
4 EVOLUTIONARY ART
Evolutionary Computation (EC) is a field within Ar-
tificial Intelligence that uses methods obtained from
evolution theory to solve problems and to perform op-
timisations (Eiben and Smith, 2008). One of the sub-
fields within EC is Genetic Programming (GP). GP
investigates how to evolve small computer programs
that perform a certain task. To this end, GP uses a
population of these programs, and one or more fit-
ness functions that evaluate the ‘fitness’ of each pro-
gram. Evolutionary art is a research field where meth-
ods from Evolutionary Computation are used to cre-
ate works of art (Bentley and Corne, 2001, Romero
and Machado, 2007). Some evolutionary art systems
use IEC or supervised fitness assignment (Rooke,
2001, Sims, 1991), and in recent years there has been
increased activity in investigating unsupervised fit-
ness assignment (Greenfield, 2003,Ross et al., 2006).
Our aesthetic measures for symmetry, compositional
balance and liveliness serve as fitness functions in
our evolutionary art system. Our system is a flexi-
ble framework built in Java that supports a number of
aesthetic measures, multi-objective optimisation us-
ing the Non-dominating Sorting Genetic Algorithm
(NSGA-II) and the Strength Pareto Evolutionary Al-
gorithm (SPEA2), with which multiple aesthetic mea-
sures can be combined. NSGA-II finds an optimal
Pareto front by using the concept of non-domination;
a solution A is non-dominated when there is no other
solution that scores higher on all of the objective
functions. Furthermore, NSGA-II uses elitism and
a mechanism to preserve diverse solution by using a
crowding distance operator. For more details, we re-
fer to (Deb et al., 2002). The system uses GP and
supports symbolic expressions (or Lisp expressions)
and Scalable Vector Graphics (SVG) as genetic rep-
resentations (we only use symbolic expressions in the
experiments in this paper). It also supports multi-
threading, whereby multiple (usually 8 on an Intel
I7 quad core machine) fitness evaluations (in unsu-
pervised evolutionary art this is probably the most
costly operation from a computational point of view)
can be performed concurrently. Many functions that
we use in our GP function set are similar to the ones
used in (Sims, 1991), (Rooke, 2001) and (Ross et al.,
2006). Table 2 summarises the used functions (in-
cluding their required number of arguments);
Table 2: Function and terminal set of our evolutionary art
system.
Terminals x,y, ephem double,
golden ratio, pi
Basic Math plus/2, minus/2, multiply/2, div/2,
mod/2
Other Math log/1, sinh/1, cosh/1, tanh/1,
atan2/2, hypot/2, log10/1, sqrt/1,
cone2/2, cone3/2, cone4/2
Relational min/2, max/2, ifthenelse/3
Bitwise and/2, or/2, xor/2
Noise perlinnoise/2, fbm/2, scnoise/2,
vlnoise/2, marble/2, turbulence/2
Boolean lessthan/4, greaterthan/4
Other parabol/2
The function set has already been described in de-
tail in previous work so refer to the original papers for
details (den Heijer and Eiben, 2010a, den Heijer and
Eiben, 2010b, den Heijer and Eiben, 2011).
5 EXPERIMENTS AND RESULTS
We performed two experiments with three different
measures; two for bilateral reflectional symmetry and
one for balance. The evolutionary parameters are
given in Table 3.
5.1 Experiments 1 and 2: Evolving
Images with Bilateral Symmetry
In our first experiment we evolved images using our
measure for bilateral symmetry (Section 3.1, Equa-
tion 13). The parameters of our experiment are given
in Table 3. We saved the 25 ‘fittest’ images from each
run (resulting in 250 images in total) and hand picked
a portfolio (representative of the 250 images) that we
show in Figure 3. From the images in the portfolio
we can conclude that all images are either perfectly
or almost perfectly bi-lateral symmetric (with respect
to the vertical axis); evolving images with (near) per-
fect bi-lateral reflectional symmetry is not difficult to
achieve using our evolutionary art system. Next, we
see that the images are diverse (not only in the port-
folio, also in the whole collection of 250 images that
was saved after the 10 runs). We think this type of
EvolvingArtusingMeasuresforSymmetry,CompositionalBalanceandLiveliness
57

Table 3: Evolutionary parameters of our evolutionary art
system used in our experiments.
Symbolic parameters
Representation Expression trees
Initialisation Ramped half-and-half (depth
between 2 and 5)
Survivor selection Tournament, Elitist (best 1)
Parent Selection Tournament
Mutation Point mutation
Recombination Subtree crossover
Fitness Aesthetic measure(s) based on
functions(s) Reflectional Symmetry
(Sec. 3.1) or Com
positional Balance (Sec. 3.2)
or a combination (NSGA-II)
Numeric parameters
Population size 200
Tournament size 3
Crossover rate 0.85
Mutation rate 0.15
Max. tree depth 8
images could be useful in graphic design, either as
background images for web pages, posters, CD cov-
ers. The static symmetric properties sometimes tend
to give the images a simplistic flavour.
A portfolio of images from experiment 2 is given
in Figure 4. In this experiment we used the ‘relaxed’
symmetry measure, that uses a gaussian function to
favour images with a symmetry of 0.8 (see Equations
9 and 15). We intended to evolve images that were
not entirely symmetrical, and from the images in Fig-
ure 4 we can see that we succeeded; the images are
more or less symmetrical from a ‘macro’ level, but
less symmetrical when looking at close range. One
could argue whether strict symmetric images are bet-
ter or worse looking than not-quite symmetric images,
but the important conclusion from this experiment is
that symmetry can be a controllable parameter in an
evolutionary art system. This notion can be built into
an automated image generation system in which the
user can specify to what degree the images should be
symmetric.
5.2 Experiment 3: Evolving Images
with Compositional Balance
We also performed an experiment with our ‘Compo-
sitional Balance’ measure (Section 3.2, Equation 15).
The configuration for this third experiment was the
same as the first two experiments (see Table 3) except
for the fitness function. Again, we saved the ‘fittest’
25 images from each run (resulting in 250 images in
total) and hand picked a representative portfolio that
we show in Figure 5.
If we look at the the portfolio in Figure 5 we see a
number of symmetric images, but we can clearly see
that not all images are symmetric. The images dif-
fer in their degree of symmetry; some are perfectly
horizontal symmetrical, whereas a number of images
show very little symmetry. We see differences be-
tween the images from experiment 3 (Figure 5) and
the first two experiments (Figures 3 and 4) but these
difference are not big. Since images with a lot of sym-
metry also display a lot of compositional balance, and
since we see a relatively large number of images with
symmetry using the aesthetic measure for composi-
tional balance, we suspect that it is ‘easier’ for our
evolutionary art system to evolve images with a lot
of symmetry that satisfy our compositional balance
fitness function than to evolve images with composi-
tional balance but without a lot of symmetry. If we
want to evolve images with balance but without sym-
metry, we will probably have to incorporate a sort of
punishment score for too much symmetry into our
aesthetic measure for compositional balance; we in-
tend to do so in future research.
5.3 Experiment 4: Combining
Symmetry with Other Aesthetic
Measures using NSGA-II
In our fourth experiment we combined three aesthe-
tic measures to evolve symmetric images. To this end
we used the well known multi-objective evolutionary
algorithm NSGA-II (Deb et al., 2002). Besides the
use of NSGA-II and the fact that we used three aes-
thetic measures instead of one, all the evolutionary
parameters were kept the same as in the previous ex-
periments, and the parameters are given in Table 3.
As the fitness functions we used the Global Contrast
Factor aesthetic measure (Matkovic et al., 2005), our
Entropy measure for liveliness (Equation 12) and our
symmetry aesthetic measure, this time set to measure
horizontal, vertical and diagonal symmetry (see Equa-
tion 8). Note that we used the strict symmetry mea-
sure from Equation 8, and not the the symmetry mea-
sure from Experiment 1 (Equation 13), since the lat-
ter aesthetic measure also incorporates the measure of
liveliness, and in our MOEA setup we want to keep
these scores separate.
The portfolio of images that we gathered from
10 runs are presented in Figure 6. From the portfo-
lio of images we can see that the measures combine
fairly well; all images show contrast and symmetry,
and most (arguably) show a fair amount of liveliness.
When we compare these images to images from pre-
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
58

Figure 3: Portfolio of images gathered from ten runs with the Bilateral Symmetry measure (Experiment 1).
Figure 4: Portfolio of images gathered from ten runs with the Bilateral Symmetry measure (Experiment 2), using a gaussian
function with µ = 0.8 and σ = 2.
Figure 5: Portfolio of images gathered from ten runs with the Compositional Balance measure (Experiment 3).
vious experiments (den Heijer and Eiben, 2010b), we
see that the images are not as dark. Experiments with
only the Global Contrast Factor as a fitness function
produced images that had very deep contrast, often
resulting a large black areas in the images. We think
that the liveliness/ entropy measure acts as an oppos-
ing force against the GCF, since the entropy mea-
sure rewards images with balanced brightness distri-
butions, and does not favour images with ‘only’ black
and white. Together they result in images that are
lively and have a fair amount of contrast. In our
fourth experiment we also used our symmetry aesthe-
tic measure, and this time we used it to evolve images
that were symmetric horizontally, vertically and diag-
EvolvingArtusingMeasuresforSymmetry,CompositionalBalanceandLiveliness
59

Figure 6: Portfolio of images gathered from ten runs with NSGA-II (Experiment 4), using Global Contrast Factor, liveliness
and symmetry (bilateral, top-down and diagonal).
onally. Some images show symmetry in all these three
directions, and almost all show symmetry in at least
two directions. We think that the first three images
in the bottom row of Figure 6 resemble tiling patterns
found in Islamic art.
6 CONCLUSIONS
Our first research question was whether it is possible
to evolve images with symmetry using an aesthetic
measure. Our first experiment confirms this. Our evo-
lutionary art systems has no problems evolving sym-
metric images. We suspect that symmetry is an image
feature that is relatively easy to satisfy using genetic
programming and our current function set.
In previous work we did experiments with an
alternative genotype representation, Scalable Vector
Graphics or SVG (den Heijer and Eiben, 2012). We
think that it will be more challenging to evolve pure
symmetric images using SVG than with symbolic ex-
pressions, but future research will have to investigate
this hypothesis. From our first and second experi-
ments we can conclude that it not only possible to
evolve symmetric images, it is also possible to con-
trol the amount of symmetry in the resulting images.
This is encouraging, since several studies have shown
that people tend to have an aesthetic preference for
symmetry, but (especially in Western art) people tend
to find too much symmetry boring, especially in an art
context. The amount of 0.8 for our ‘optimal amount
of symmetry’ was chosen by us, but we think the ac-
tual threshold value is less important in our experi-
ment; it is important to know that symmetry can be a
controllable parameter in an evolutionary art system.
Our second research question was whether it was
possible to evolve aesthetically pleasing images using
our aesthetic measure for compositional balance. Our
third experiment resulted in a number of interesting
images, but many images were ‘just symmetrical’ and
relative few were ‘balanced and not symmetrical’. We
think our aesthetic measure for balance using an im-
age distance function is a good starting point, but this
aesthetic measure would benefit from additional con-
straint, like a penalty function for having too much
symmetry. We also think that our aesthetic measure
for balance might be more useful in images with a
composition; the images that we evolved using our
symbolic expression genotype are all abstract images,
with no representational content.
We intend to do further research in the applica-
tion of this aesthetic measure in our evolutionary art
system using our SVG genotype, in which the result-
ing images have objects, composition and representa-
tional content.
Our third research question was whether it was
possible to combine our aesthetic measure for sym-
metry with other, existing aesthetic measures to pro-
duce new and surprising images. Our fourth experi-
ment confirms this. The images of the fourth experi-
ment show the effects of the different aesthetic mea-
sures. The images from Figure 6 show (in varying de-
grees) contrast, symmetry and liveliness. From these
experiments we can conclude that an aesthetic mea-
sure for symmetry combines relatively easy with ex-
isting aesthetic measures. Furthermore, we think that
aesthetic measures for symmetry and compositional
balance should be combined with other aesthetic mea-
sures; evolving images with only a measure for sym-
metry of compositional balance would most likely re-
sult in monotonous, often monochrome images.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
60

REFERENCES
Arnheim, R. (1988). The power of the center : a study of
composition in the visual arts. University of Califor-
nia Press.
Baluja, S., Pomerleau, D., and Jochem, T. (1994). Towards
automated artificial evolution for computer-generated
images. Connection Science, 6:325–354.
Bauerly, M. P. and Liu, Y. (2005). Development and val-
idation of a symmetry metric for interface aesthetics.
Proceedings of the Human Factors and Ergonomics
Society Annual Meeting, 49(5):681–685.
Bauerly, M. P. and Liu, Y. (2008). Effects of symmetry and
number of compositional elements on interface and
design aesthetics. International Journal of Human-
Computer Interaction, 24(3):275–287.
Bentley, P. J. and Corne, D. W., editors (2001). Creative
Evolutionary Systems. Morgan Kaufmann, San Ma-
teo, California.
Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T.
(2002). A fast elitist multi-objective genetic algo-
rithm: NSGA-II. IEEE Transactions on Evolutionary
Computation, 6:182–197.
den Heijer, E. and Eiben, A. (2010a). Comparing aesthe-
tic measures for evolutionary art. In Applications of
Evolutionary Computation, pages 311–320.
den Heijer, E. and Eiben, A. (2010b). Using aesthetic mea-
sures to evolve art. In IEEE Congress on Evolutionary
Computation, pages 311–320.
den Heijer, E. and Eiben, A. (2011). Evolving art using mul-
tiple aesthetic measures. In EvoApplications, LNCS
6625, 2011, pages 234–243.
den Heijer, E. and Eiben, A. (2012). Evolving pop art using
scalable vector graphics. In EvoMusart 2012, Evo-
lutionary and Biologically Inspired Music, Sound, Art
and Design, LNCS 7247, pages 48–59, Malaga, Spain.
Dutton, D. (2009). The Art Instinct. Oxford University
Press.
Eiben, A. E. and Smith, J. E. (2008). Introduction to
Evolutionary Computing (Natural Computing Series).
Springer.
Etcoff, N. (1999). Survival of the prettiest: the science of
beauty. Anchor Books.
Greenfield, G. R. (2003). Evolving aesthetic images us-
ing multiobjective optimization. In Proceedings of the
2003 Congress on Evolutionary Computation CEC
2003, pages 1903–1909. IEEE Press.
Ling, D. N. C., Samsudin, A., and Abdullah, R. (2000).
Aesthetic measures for assessing graphic screens. J.
Inf. Sci. Eng., 16(1):97–116.
Locher, P. and Nodine, C. (1989). The perceptual value of
symmetry. Computers & Mathematics with Applica-
tions, 17(4–6):475–484.
Machado, P. and Cardoso, A. (1998). Computing aesthetics.
In Proceedings of the Brazilian Symposium on Artifi-
cial Intelligence, SBIA-98, pages 219–229. Springer-
Verlag.
Machado, P. and Cardoso, A. (2002). All the truth about
nevar. Applied Intelligence, 16(2):101–118.
Matkovic, K., Neumann, L., Neumann, A., Psik, T., and
Purgathofer, W. (2005). Global contrast factor-a new
approach to image contrast. In Neumann, L., Sbert,
M., Gooch, B., and Purgathofer, W., editors, Compu-
tational Aesthetics, pages 159–168. Eurographics As-
sociation.
Reber, R., Schwarz, N., and Winkielman, P. (2004). Pro-
cessing fluency and aesthetic pleasure: is beauty in
the perceiver’s processing experience? Personality
and Social Psychology Review, 8(4):364–382.
Rigau, J., Feixas, M., and Sbert, M. (2008). Informational
aesthetics measures. IEEE Computer Graphics and
Applications, 28(2):24–34.
Romero, J. and Machado, P., editors (2007). The Art of Arti-
ficial Evolution: A Handbook on Evolutionary Art and
Music. Natural Computing Series. Springer Berlin
Heidelberg.
Rooke, S. (2001). Eons of genetically evolved algorithmic
images. In (Bentley and Corne, 2001), pages 339–365.
Ross, B., Ralph, W., and Zong., H. (2006). Evolutionary
image synthesis using a model of aesthetics. In IEEE
Congress on Evolutionary Computation (CEC) 2006,
pages 1087–1094.
Sims, K. (1991). Artificial evolution for computer graphics.
SIGGRAPH ’91: Proceedings of the 18th annual con-
ference on Computer graphics and interactive tech-
niques, 25(4):319–328.
Stricker, M. and Orengo, M. (1995). Similarity of color
images. In Storage and Retrieval of Image and Video
Databases III, Vol. 2, pages 381–392.
Weyl, H. (1983). Symmetry. Princeton University Press.
White, A. (2011). The Elements of Graphic Design (Second
Edition). Allworth Press.
EvolvingArtusingMeasuresforSymmetry,CompositionalBalanceandLiveliness
61
