Parallel Batch Pattern Training of Recirculation Neural Network

Volodymyr Turchenko

, Vladimir Golovko

and Anatoly Sachenko

Research Institute of Intelligent Computer Systems, Ternopil National Economic University,

3 Peremoga Square, 46009, Ternopil, Ukraine

Laboratory of Artificial Neural Networks, Intelligent Information Technologies Department,

Brest State Technical University, Moskowskaja 267, 224017, Brest, Belarus

Keywords: Parallel Batch Pattern Training, Recirculation Neural Network, Parallelization Efficiency.

Abstract: The development of a parallel batch pattern back propagation training algorithm of a recirculation neural

network is presented in this paper. The model of a recirculation neural network and usual sequential batch

pattern algorithm of its training are theoretically described. An algorithmic description of the parallel

version of the batch pattern training method is presented. The parallelization efficiency of the developed

parallel algorithm is investigated on the example of data compression and principal component analysis.

The results of the experimental researches show that the developed parallel algorithm provides high

parallelization efficiency on a parallel symmetric multiprocessor computer system. It allows applying the

developed parallel software for the facilitation of scientific research of neural network-based intrusion

detection system for computer networks.

1 INTRODUCTION

Artificial neural networks (NNs) have excellent

abilities to model difficult nonlinear systems. They

represent a very good alternative to traditional

methods for solving complex problems in many

fields, including image processing, predictions,

pattern recognition, robotics, optimization, etc

(Haykin, 2008). However, most NN models require

high computational load in the training phase (on a

range from several hours to several days). This is,

indeed, the main obstacle to face for an efficient use

of NNs in real-world applications. The use of

general-purpose high performance computers,

clusters and computational grids to speed up the

training phase of NNs is one of the ways to

outperform this obstacle. Therefore the research of a

parallelization efficiency of NNs parallel training

algorithms on such kind of parallel systems is still

remaining an urgent research problem.

Taking into account the parallel nature of NNs,

many researchers have already focused their

attention on NNs parallelization on specialized

computing hardware and transputers (Mahapatra et

al, 1997, Hanzalek, 1998), but these solutions

require an availability of the mentioned devices for

the use by wide scientific community. Instead

general-purpose high performance computers and

computational clusters are widely used now for

scientific experiments and modeling using remote

access.

There are developed several grid-based

frameworks for NNs parallelization (Vin et al.,

2005); (Krammer et al., 2006), however they do not

deal with parallelization efficiency issues. The

authors of (De Llano, 2010) investigate parallel

training of multi-layer perceptron (MLP) on SMP

computer, cluster and computational grid using MPI

(Message Passing Interface) parallelization. They

have researched big NN models which process huge

number of the training patterns (around 20000)

coming from Large Hadron Collider. However their

implementation of relatively small MLP architecture

16-10-10-1 (16 neurons in the input layer, two

hidden layers with 10 neurons in each layer and one

output neuron) with 270 internal connections

(number of weights of neurons and their thresholds)

does not provide positive parallelization speedup

due to large communication overhead, i.e. the

speedup is less than 1.

The development of parallel training algorithm

of Elman’s simple recurrent neural network (RNN)

based on Extended Kalman Filter on multicore

processor and Graphic Processing Unit (GPU) is

presented in (Cernansky et al., 2009). The author has

644

Turchenko V., Golovko V. and Sachenko A..

Parallel Batch Pattern Training of Recirculation Neural Network.

DOI: 10.5220/0004150206440650

In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ANNIIP-2012), pages 644-650

ISBN: 978-989-8565-21-1

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

showed a reduction of the RNN training time using a

GPU solution (4 times better performance was

achieved), however it is impossible to assess the

parallelization efficiency of this parallel algorithm

because it was not clearly stated a number of GPU

threats used for parallelization. The authors of

(Lotric et al., 2009) have presented the development

of parallel training algorithm of fully connected

RNN based on linear reward penalty correction

scheme.

The authors of (Turchenko and Grandinetti,

2010); (Turchenko et al., 2012) have researched the

problem of parallelization of NN training on the

example of feed-forward NNs with direct (MLP) and

inverse (RNN) connections. They have developed

the parallel batch pattern back propagation (BP)

training algorithm for both types of NNs and

presented their good parallelization efficiency on

general-purpose parallel computers and

computational clusters.

Meantime Recirculation Neural Networks

(RCNN) are successfully used for data compression

and decompression, image processing and Principal

Component Analysis (PCA) (Golovko et al., 2001);

(Bryliuk et al., 2001). However, the parallelization

techniques for RCNN training are not enough

addressed by the world’s scientific community yet.

Our analysis has shown a lack of research papers in

this issue.

The goal of this paper is to present the

development of a parallel training algorithm for

recirculation neural network and research its

parallelization efficiency on a general-purpose

parallel computer. The rest of this paper is ordered

as follows: Section 2 details the mathematical

description of a batch pattern back propagation

training algorithm for RCNN, Sections 3 describes

the parallel implementation of this algorithm,

Section 4 presents the obtained experimental results

and concluding remarks in Section 5 finishes this

paper.

2 BATCH PATTERN BP

TRAINING ALGORITHM OF

RECIRCULATION NN

In our previous research we have proven that the

parallelization of a batch pattern training approach is

efficient on general-purpose parallel computers and

computational clusters instead of the parallelization

on the level of neuron or synapses of neurons

(Turchenko et al., 2010); (Turchenko et al., 2009) on

the examples of MLP and RNNs. The batch pattern

training algorithm updates neurons’ weights and

thresholds at the end of each training epoch, i.e. after

processing of all training patterns, instead of

updating weights and thresholds after processing of

each pattern in the usual sequential training mode.

Therefore it is expedient to apply this parallelization

scheme to a RCNN.

Recirculation neural network (Fig. 1) performs

compression of the input pattern space

to obtain

the principal components. The principal components

are the output values

Y of the neurons of the hidden

layer. Then the RCNN restores the compressed data

(principal components) into the output vector

The output value of the RCNN can be formulated as:

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⋅

′

∑∑

iijjii

xwFwFx

(1)

where

is the number of neurons in the hidden

layer,

′

is the weight of the synapse from the

neuron

of the hidden layer to the neuron

of the

output layer,

is the number of neurons in the input

and output layers,

is the weight from the input

neuron

to neuron

in the hidden layer,

x are the

input values (Golovko et al., 2001).

Note that the principal components are

calculated by expression

⎟

⎠

⎞

⎜

⎝

⎛

∑

iijj

xwFy

. The

logistic activation function

−

)(

is used

for the neurons of the hidden (

F ) and output layers

(

F ).

′

Figure 1: The structure of a recirculation neural network.

The batch pattern BP training algorithm consists

of the following steps (Golovko et al., 2001):

1 Set the desired Sum Squared Error (SSE) to a

value

min

E and the number of training epochs

;

ParallelBatchPatternTrainingofRecirculationNeuralNetwork

645

2 Initialize the weights and the thresholds of the

neurons with values in range (-0.1…0.1) (Golovko

et al, 1999);

3 For the training pattern

3.1. Calculate the output value

)(tx

expression (1);

3.2. Calculate the errors of the output neurons

))()(()( txtxt

−=

, where

)(tx

is the

output value of the

output neuron and

)(tx

the value with index

of the input pattern of the

RCNN;

3.3. Calculate the errors of the hidden layer

neurons

∑

′

⋅

′

⋅=

iji

tSFtwtt

))(()()()(

γγ

where

)(tS

is the weighted sum of the

output

neuron,

′

is a derivative of the logistic

activation function with

)(tS

argument;

3.4. Calculate the delta weights and delta

thresholds of all neurons and add the result to the

value of the previous pattern

)())(()(

tytSFtwsws

ijiji

⋅

′

⋅+

′

Δ=

′

)())(()(

txtSFtwsws

jijij

⋅

′

⋅+Δ=Δ

, where

)(tS

and

)(ty

are the weighted sum and the

output value of the neuron

of the hidden layer

respectively;

3.5. Calculate the SSE using

()

)()(

)( txtxtE

−=

;

4 Repeat the step 3 above for all training patterns

{}

PTpt ,...,1∈ , P

is the size of the training

set;

5 Update the weights and thresholds of neurons

using expressions

jijiji

wstwPTw

′

⋅

−

′

)()0()(

and

ijijij

wstwPTw Δ⋅−= )()0()(

, where

)0(

′

and

)0(

are the values of the weights of the

hidden and output layers from the previous training

epoch,

)(

and )(

are the learning rates for the

neurons of the hidden and output layers respectively;

6 Calculate the total SSE

)(tE

on the training

epoch

using

∑

tEtE

)()( ;

7 If

)(tE

is greater than the desired error

min

then increase the number of training epochs to

and go to step 3, otherwise stop the training process.

3 PARALLEL

IMPLEMENTATION OF

BATCH PATTERN BP

TRAINING ALGORITHM OF

RCNN

Similarly to the parallel batch pattern training

algorithm of an MLP presented in (Turchenko et al.,

2012); (Turchenko et al., 2009), sequential execution

of points 3.1-3.5 above for all training patterns in the

training set could be parallelized, because the sum

operations

′

and

are independent of each

other. For the development of the parallel algorithm

all the computational work should be divided among

the Master (executing assigning functions and

calculations) and the Workers (executing only

calculations) processors.

The algorithms for Master and Worker

processors are depicted in Fig. 2. The Master starts

with definition (i) the number of patterns PT in the

training data set and (ii) the number of processors p

used for the parallel executing of the training

algorithm. The Master divides all patterns in equal

parts corresponding to the number of the Workers

and assigns one part of patterns to itself. Then the

Master sends to the Workers the numbers of the

appropriate patterns to train.

Each Worker executes the following operations

for each pattern pt of the PT/p patterns assigned to

it:

1. calculate the points 3.1-3.5 and 4, only for its

assigned number of training patterns. The values of

the partial sums of delta weights

′

and

wsΔ

are

calculated there;

2. calculate the partial SSE for its assigned number

of training patterns.

After processing all assigned patterns, only one all-

reduce collective communication operation (it

provides the summation as well) is executed.

Synchronization with other processors is

automatically provided by internal implementation

of this all-reduce operation (Turchenko et al., 2010).

However from the algorithmic point of view it is

showed as an independent operator in Fig. 2 before

the operation of data reduce. Then the summarized

values

′

and

are sent to all processors

working in parallel. Instead of three communication

messages in (De Llano et al., 2010), using only one

all-reduce collective communication message, which

also returns the reduced values back to the Workers,

allows decreasing a communication overhead in this

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

646

point. Then the summarized values

′

and

are placed into the local memory of each processor.

Each processor uses these values for updating the

weights according to the point 5 of the algorithm

above. These updated weights will be used on the

next iteration of the training algorithm. As the

summarized value of

)(tE is also received as a

result of the reducing operation, the Master decides

whether to continue the training or not.

Yes

Star

Read the in

ut data

Update

′

an d

w ,

according to p.5

Reduce and Sum

′

Δ ,

wsΔ , )(tE from all

processors and send it

back to them

min

)( EtE >

End

)

Star

Read the in

ut data

Receive PT/p patterns

from Master

Define PT and p

Send PT/p patterns to

each Worker

Calculate p.3 and p.4 for

own training patterns

Synchronization with

other Workers

Reduce and Sum

ws ′Δ ,

wsΔ , )(tE fro m all

Workers & Master

Calculate p.3 and p.4 for

assigned training patterns

Synchronization with

other Worker s & Master

Update

′

and

according to p.5

Message to

finish work?

End

Figure 2: The algorithms of the Master (a) and the Worker

(b) processors.

The software routine is developed using C

programming language with the standard MPI

functions. The parallel part of the algorithm starts

with the call of MPI_Init() function. An

MPI_Allreduce() function reduces the deltas of

weights

′

and

wsΔ

, summarizes them and

sends them back to all processors in the group.

Since the weights and thresholds are physically

located in the different matrixes of the software

routine, we have done pre-encoding of all data into

one communication message before sending and

reverse post-decoding the data to the appropriate

matrixes after message receiving in order to provide

only one physical call of the function

MPI_Allreduce() in the communication section of

the algorithm. Function MPI_Finalize() finishes the

parallel part of the algorithm.

4 EXPERIMENTAL RESULTS

The application task of data compression and PCA

within NN-based method of intrusion detection and

classification in computer networks (Vaisekhovich

et al., 2009) is used for the experimental research of

the parallelization efficiency of the developed

parallel algorithm. NN-based detector consists of

two NNs (Fig. 3): (i) recirculation neural network is

used for finding 12 principal components by

compression of input 41-element record about

network intrusion and (ii) multilayer perceptron,

which takes these 12 principal components in order

to detect whether there was an attack or not. The

choice of the 12 principal components has proven in

(Vaisekhovich et al., 2009); (Komar et al., 2011)

allowing to significantly improve the true positive

detection rate of the detector and decrease the

complexity of the MLP model. Also other

architectures of the detector are available

(Vaisekhovich et al., 2009) which consist of multiple

RCNN+MLP models, each model for separate type

of the network intrusion.

RCNN

MLP

ot attack

Attac

. . .

Figure 3: NN-based intrusion detector.

The database KDD cup 99 (KDD, 1999)

containing information about network intrusions is

used for the training and testing of this NN-based

detector. This database is very huge. Therefore only

10% part of it (500 thousand records) is used on

practice. The 6168 records of network intrusions

have been used for the NN-based detector training in

(Vaisekhovich et al., 2009). However, bigger

number of the processed record leads to the better

classification ability of the NN-based detector.

We have used only 2203 records, the content of

the file with the description of the DoS attacks, for

our experiments. We have chosen this not very big

number of the input training patterns because with

the increasing the number of input patterns the

parallelization efficiency of the batch pattern

training algorithm normally is increased (Turchenko

et al., 2012). Thus the RCNN architecture with 41

input, 12 hidden and 41 output neurons (984

connections) is used for the experiments

compressing 2203 input patterns about DoS attacks.

The RCNN was trained 10

training epochs, the SSE

= 0.087 was reached. The learning rates

)(

and

)(

were fixed to 0.05.

ParallelBatchPatternTrainingofRecirculationNeuralNetwork

647

The SMP parallel supercomputer Skopa (TYAN

Transport VX50), located in the Research Institute

for Intelligent Computer Systems, Ternopil,

Ukraine, is used for the computations. It consists of

two identical blocks VX50_1 and VX50_2. We have

used only one block which consists of four 64-bit

dual-core processors AMD Opteron 8220 with a

clock rate of 2800 MHz and 16 GB of local RAM.

Each processor has a primary data and instruction

cache of 128 Kb and the second level cache of 2 Mb.

There are 4 RAM access channels at the block. The

speed of data transfer between processors inside

block is 2.0 GT/s. The supercomputer is operating

under Linux operation system, the MPICH2 message

passing library (MPICH2, 2011) is installed for

parallelization.

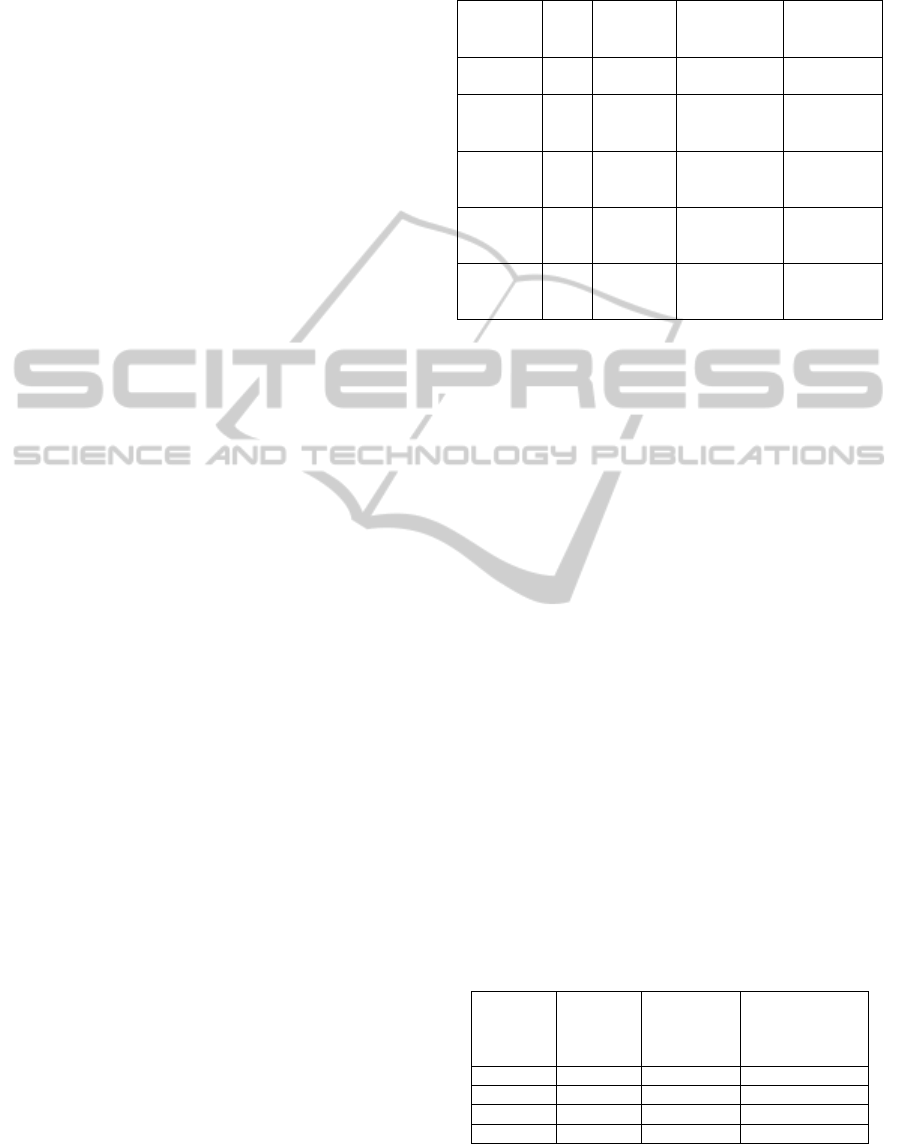
The results of sequential and parallel routine

execution are presented in Table 1. The column

“Execution time” shows the total execution time of

the routine, the column “Computation time” shows

the execution time of the computational part of the

algorithm, the column “Communication time” shows

the execution time of the communication part of the

algorithm. As we can see, the sequential routine

compiled by the standard Linux compiler cc, is

executed for 1347,18 seconds, when the parallel

version, compiled by the MPI compiler mpicc, is

executed for only 240,06 seconds on 1 processor of

the parallel computer. This behavior can be

explained by the fact, that mpicc compiler is better

designed to account the features of the parallel

machine and can produce faster execution code than

standard cc. Therefore for the research of the

parallelization efficiency we will compare the

execution time of the parallel routine on 2,4,8

processors with the execution time of the parallel

routine on 1 processor. Thus the expressions

S=Ts/Tp, (2)

E=S/p×100% (3)

are used to calculate a speedup and efficiency of

parallelization, where Ts is the time of sequential

executing the parallel routine on 1 processor, Tp is

the time of parallel executing of the same routine on

p processors of parallel computer.

The results of speedup and efficiency analysis

(Fig. 4) have shown that the developed batch pattern

parallel algorithm of RCNN training provides

practically linear speedup and high parallelization

efficiency. It allows successfully using this parallel

algorithm within developing PaGaLiNNeT library

(PaGaLiNNeT, 2011) for the intensification of

scientific research on network intrusion detection

approaches using neural networks.

Table 1: Execution results of the sequential and parallel

routines.

Routine CPUs

Execution

time, sec

Computation

time, sec

Communi-

cation time,

sec

Sequential

cc compiler

1 1347.18 n/a n/a

Parallel

mpicc

compiler

1 240.06 239.99 0.03

Parallel

mpicc

compiler

2 123.96 120.47 3.44

Parallel

mpicc

compiler

4 64.36 60.76 3.56

Parallel

mpicc

compiler

8 33.45 28.44 4.90

We have used the developed parallel batch

pattern training algorithm of RCNN for the research

of reconstruction accuracy of the input data (quality

of finding the principal components). The goal of

this research is to find the limitation values of the

training epochs and SSE which provide reasonable

(the lowest) reconstruction accuracy of the input

data in terms of execution time. The results of this

research are presented in Table 2. The average

reconstruction error of the 2203 patterns is presented

in the last column of the Table. These results were

obtained by the developed software routine on 8

processors of the Skopa supercomputer having

approximately 7-time speedup of the execution time.

The analysis of the results has shown that most

reasonable to train RCNN by 10

epochs which

provide average relative reconstruction error 14.9 %,

because 10

epochs provides 10-time bigger

execution time with just 1% decreasing of the

reconstruction error. The analysis of the numerical

results of the reconstruction error has shown that, for

the case of 10

training epochs, the 83% of the

reconstruction errors of all the 41 values of each

2203 record are less than 1% and this 14.9% result is

caused by “outliers”.

Table 2: Obtained average relative reconstruction errors

by different numbers of training epochs.

Number

of epochs

Reached

SSE

Execution

time, sec

Average

relative

reconstruction

error, %

0.087 33.45 37.0

0.078 339.83 19.0

0.052 3385.12 14.9

0.019 34412.39 13.8

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

648

2 4 8

CPUs

Times

Speedup for 984 connections, 2203 patterns

2 4 8

CPUs

Percents

Efficiency for 984 connections, 2203 patterns

Figure 4: Speedup (2) and parallelization efficiency (3) of the parallel algorithm.

Also the 7-time faster execution time of the

developed parallel routine allowed us to speed up

our research in finding the dependence between the

average reconstruction error and the number of the

principal components (the number of neurons of the

hidden layer). The results of this research at 10

training epochs on 8 processors of the Skopa

supercomputer are collected in Table 3. As we can

see, the average reconstruction error is decreasing at

the increasing the number of the principal

components. Therefore the correct number of the

principal components should be chosen on the base

of the classification results obtained by the second

NN - MLP classifier (see Fig. 3).

Table 3: Results of research the number of the principal

components.

Number of

principal

components

Reached

SSE

Execution

time, sec

Average

relative

reconstruction

error, %

6 0.0852 200.91 21.0

8 0.0850 236.67 19.7

10 0.0842 308.28 19.5

12 0.0780 339.83 19.0

14 0.0765 353.77 18.4

16 0.0749 402.42 18.1

18 0.0779 463.75 17.9

20 0.0805 504.60 17.7

24 0.0817 596.54 17.6

5 CONCLUSIONS

The development of the parallel batch pattern back

propagation training algorithm of recirculation

neural network and the research of its parallelization

efficiency on the parallel supercomputer are

presented in this paper. The algorithm is well

designed because it provides high parallelization

efficiency on the level of 97-89% on 2-8 processors

of the SMP supercomputer. The use of the

developed parallel algorithm has allowed facilitating

the scientific research on the development of neural

network-based classifiers for computer network

intrusion detection system.

The future direction of research can be

considered as investigation of the parallelization

efficiency of the developed algorithm with the use of

adaptive learning rates under a grid middleware

environment.

ACKNOWLEDGEMENTS

This research is financially supported by the Marie

Curie International Incoming Fellowship grant

(return phase) of the corresponding author Dr.

Volodymyr Turchenko, Ref. Num. 221524-908524

“PaGaLiNNeT - Parallel Grid-aware Library for

Neural Networks Training", within the 7

European

Community Framework Programme. The authors

ParallelBatchPatternTrainingofRecirculationNeuralNetwork

649

would like to acknowledge the help of Mr. Myroslav

Komar, the Research Institute of Intelligent

Computer Systems, TNEU for the providing

formatted data of KDD99 database ready for the

experiments.

REFERENCES

Haykin, S., 2008. Neural networks and learning machines.

Prentice Hall, 936 p.

Mahapatra, S., Mahapatra, R., Chatterji B., 1997. A

Parallel Formulation of Back-propagation Learning on

Distributed Memory Multiprocessors. Parallel

Computing. Vol. 22, No. 12, pp. 1661-1675.

Hanzálek, Z., 1998. A Parallel Algorithm for Gradient

Training of Feed-forward Neural Networks. Parallel

Computer. Vol. 24, No. 5-6, pp. 823-839.

Vin, T.K., Seng, P.Z., Kuan, M.N.P., Haron, F., 2005. A

Framework for Grid-based Neural Networks.

Proceedings of First International Conference on

Distributed Frameworks for Multimedia Applications.

pp. 246-250.

Krammer, L., Schikuta, E., Wanek, H., 2006. A Grid-

based Neural Network Execution Service Source.

Proceedings of 24

IASTED International Conference

on Parallel and Distributed Computations and

Networking. pp. 35-40.

De Llano, R.M., Bosque, J.L., 2010. Study of Neural Net

Training Methods in Parallel and Distributed

Architectures. Future Generation Computer Systems.

Vol. 26, Issue 2, pp. 183-190.

Cernansky M., 2009. Training Recurrent Neural Network

Using Multistream Extended Kalman Filter on

Multicore Processor and Cuda Enabled Graphic

Processor Unit. Lecture Notes in Computer Science.

Volume 5768, Part I, pp. 381-390.

Lotric, U., Dobnikar, A., 2009. Parallel Implementations

of Recurrent Neural Network Learning. M.

Kolehmainen et al. (Eds.): ICANNGA 2009, LNCS

5495. Springer-Verlag, Berlin, Heidelberg, pp. 99–

108.

Turchenko, V., Grandinetti, L., 2010. Parallel Batch

Pattern BP Training Algorithm of Recurrent Neural

Network. Proceedings of the 14th IEEE International

Conference on Intelligent Engineering Systems. Las

Palmas of Gran Canaria, Spain, pp. 25-30.

Turchenko, V., Grandinetti, L., Sachenko, A., 2012.

Parallel Batch Pattern Training of Neural Networks on

Computational Clusters. Proceedings of the 2012

International Conference on High Performance

Computing & Simulation HPCS 2012. July 2 – 6,

Madrid, Spain, in press.

Golovko, V., Galushkin A., 2001. Neural Networks:

training, models and applications, Moscow,

Radiotechnika (in Russian).

Bryliuk, D., Starovoitov, V., 2001. Application of

Recirculation Neural Network and Principal

Component Analysis for Face Recognition. The 2nd

International Conference on Neural Networks and

Artificial Intelligence. Minsk, BSUIR, pp.136-142.

Turchenko, V., Grandinetti, L., 2009. Efficiency Research

of Batch and Single Pattern MLP Parallel Training

Algorithms. Proceedings 5th IEEE International

Workshop on Intelligent Data Acquisition and

Advanced Computing Systems IDAACS2009. Rende,

Italy, pp. 218-224.

Golovko, V., Gladyschuk, V., 1999. Recirculation Neural

Network Training for Image Processing. Advanced

Computer Systems. pp. 73-78.

Turchenko, V., Grandinetti, L., Bosilca, G., Dongarra, J.,

2010. Improvement of parallelization efficiency of

batch pattern BP training algorithm using Open MPI.

Elsevier Procedia Computer Science 2010. Volume 1,

Issue 1, pp. 525-533.

Vaitsekhovich, L., Golovko, V., 2009. Intrusion Detection

in TCP/IP Networks Using Immune Systems

Paradigm and Neural Network Detectors. XI

International PhD Workshop OWD 2009. pp. 219-224.

Komar, M., Golovko, V., Sachenko, A., Bezobrazov S.,

2011. Intelligent system for detection of networking

intrusion. Proceedings of the 6th IEEE International

Conference on Intelligent Data Acquisition and

Advanced Computing Systems IDAACS-2011. Prague

(Czech Republic), V1, pp. 374-377.

KDD Cup Competition 1999. – Information on:

http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.ht

ml.

MPICH2, 2011. http://www.mcs.anl.gov/research/projects

/mpich2/

PAGaLiNNeT, 2011. http://uweb.deis.unical.it/turchenko/

research-projects/pagalinnet/

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

650