FPGA Implementation of Hodgkin-Huxley Neuron Model

Safa Yaghini Bonabi

, Hassan Asgharian

, Reyhaneh Bakhtiari

1,3

, Saeed Safari

and Majid Nili Ahmadabadi

1,3

School of Electrical and Computer Engineering, College of Engineering, University of Tehran, Tehran, Iran

Department of Computer Engineering, IUST, Tehran, Iran

School of Cognitive Sciences, Institute for Research in Fundamental Sciences (IPM), Tehran, Iran

Keywords: Hodgkin-Huxley, FPGA, VHDL, MATLAB.

Abstract: In this paper an implementation of Hodgkin-Huxley single neuron is provided. Unlike almost all of the

existing implementations, the arithmetic logics are implemented with computation techniques (i.e.

CORDIC) and look-up-tables (LUTs) are used only in few modules. This makes our design more robust and

flexible to simulate the functionality of a large network of neurons. Most of the previous works are based on

the software implementations which overshadow the parallel nature of the neural system or using LUTs for

hardware implementation which needs more space and also limited flexibility. In this paper, an FPGA is

selected as our hardware implementation platform to provide an appropriate reconfigurable platform for

simulating the functionality of a network of neurons. We validated our design based on our high level

implementation of Hodgkin-Huxley neuron in MATLAB and report our implementation results based on

Xilinx SPARTAN 3 FPGA in Xilinx ISE Design Suite.

1 INTRODUCTION

There has been a recent interested in computational

neuroscience, which tries to reveal how the brain

processes information, based on the functionality

and the relationship between different parts of the

nervous system. Neurons are considered as the basic

building blocks of the nervous system. They are

excitatory/inhibitory cells that receive electrical

signals from other neurons, combine them, and

transmit them to other neurons through their short or

long axons. To perform a specific function, up to

thousands neurons may interconnect to each other in

a neural network. It is of special interest to develop

computational tools to simulate the behaviour of

neurons, and verify the theories that were proposed

to justify the results of experiments (Kandel et al.,

2000).

Transient, as well as the steady state, response of

each neuron affects the behavior of all neurons

connected to it. This dynamic interaction among the

neurons seems to be very important in functionality

of the neural networks. Such an interaction cannot

be implemented in a serial system. Therefore,

modeling parallelism as well as dynamic interaction

of the neurons is essential.

A neuron can be modeled in two ways: software

simulation and hardware implementation. Software

simulation has a serial nature (Li et al., 2010) and, as

a result, simulation of transient interaction of the

neurons is very difficult in software simulation. In

addition, it is slower in comparison to the hardware

implementation. Moreover, due to the required large

number of interconnected neurons in a neural

network, hardware implementation provides the

results in a reasonable time. There are two different

hardware implementation approaches: analog and

digital implementations. Digital implementation is

widely used because of its lower noise sensitivity,

more flexibility, easier testability and repeatability

(Muthuramalingam et al., 2008). In addition, digital

implementation has lower design time and cost

(Gatet et al., 2009). Nevertheless, it is easier to

model dynamic interaction of the neurons in

analogue systems but the main deficiency of digital

implementation is the limited available area which

demands more optimal designs.

There are different alternatives for digital

implementation; including ASIC, DSP, and FPGA.

The ASIC-based implementation is not suitable

because it is not reconfigurable and it cannot be

changed after manufacturing (Wanhammar, 1999).

The key feature of DSP-based implementation is

522

Yaghini Bonabi S., Asgharian H., Bakhtiari R., Safari S. and Nili Ahmadabadi M..

FPGA Implementation of Hodgkin-Huxley Neuron Model.

DOI: 10.5220/0004152605220528

In Proceedings of the 4th International Joint Conference on Computational Intelligence (NCTA-2012), pages 522-528

ISBN: 978-989-8565-33-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

that, it is sequential and the neurons cannot be easily

modelled in a parallel architecture. In other words,

DSP-based systems are special purpose

implementation of processor-based system. FPGAs

benefit from reconfigurable and parallel architecture

and these properties make them the best candidate

for neuron’s implementation (Muthuramalingam et

al., 2008).

Several FPGA implementations of biological

neurons have been proposed so far (Graas et al.,

2004); (Mokhtar et al., 2008); (Rice et al., 2009);

(Pourhaj and Teng, 2010) that most of them

implemented Izhikevich models (Mokhtar et al.,

2008); (Rice et al., 2009). In this paper, we are

interested to implement a more biologically

plausible neuron model. For this purpose, the

Hodgkin-Huxley (H-H) neuron model is chosen. In

(Graas et al., 2004); (Pourhaj and Teng, 2010), the

H-H neuron model has been implemented. E. L.

Graas et al. (Graas et al., 2004) used look-up-table

(LUT) instead of implementing equations for

calculating the critical parts of the implementation.

So, this type of implementation needs a large size of

memory to pre-compute the required results (of

course with limited number of bits) and save them in

LUTs which reduces the final accuracy because of

constraints on the memory size. In addition, in

(Graas et al., 2004) a neuron was implemented using

System Generator but it is obvious that automatic

software tools cannot produce an optimal hardware.

P. Pourhaj et al. (Pourhaj and Teng, 2010) used LUT

to implement different parts, which has a side effect

on the final accuracy of the implementation. For

instance, the LUT-based implementation of some

equations with the exponential terms has not (and

also can not) enough accuracy.

In this paper the H-H neuron model is used for

implementation. We employ MATLAB for high

level design of a single neuron’s behavior and use

the results as a gold standard to check our

implementation on FPGA. The rest of the paper is

organized as follows. In Section 2 the H-H model is

briefly explained. The FPGA implementation details

are discussed in Section 3. In Section 4 experimental

results are provided and finally Section 5 concludes

the work and provides the future works.

2 HODGKIN HUXLEY MODEL

In a series of experiments carried out on the squid

giant axon, Hodgkin and Huxley introduced a model

to explain the process of action potentials generation

in the neuron, based on ionic current through the

membrane (Hodgkin and Huxley, 1952). Voltage-

dependent ion channels for potassium and sodium

control flow of these ions. All other ions (mostly

chloride ions) that flow through the neuron

membrane constitute the leak current. Concentration

and electrical potential gradients are two forces

driving ions passing through the membrane

channels. The electrical potential, in which these two

forces become equal and the net flowing currents

becomes zero, is called equilibrium rest state. It is

about -65 mV and may vary in different neurons. If

the neuron is stimulated by an external current, or

through other up-stream neurons, the potential of

neurons increases to a positive value and after a

short time falls back to the equilibrium rest potential

(Izhikevich, 2007). This abrupt change in membrane

voltage is called action potential. The Hodgkin &

Huxley proposed circuit for squid giant axon is

shown in figure 1, and equation (1) gives the relation

between input current and the membrane voltage.

Figure 1: Hodgkin & Huxley proposed circuit for squid

giant axon. g

& g

, are voltage-dependent conductance.

The complete set of H-H current’s equations

according to (Izhikevich, 2007) comes in (1) to (4).

CV = - - -

IIII

ext K Na L



(1)

Where, the potassium current,

is given by

equation (2).

=n(V-)

(2)

is the potassium current with four activation

gates which is shown by n

is the sodium current that is defined in

equation (3). It has three activation gates (m

) and

one inactivation gate (h).

=mh(V-)

aNa

(3)

is the ohmic leak current which is given in

equation (4).

FPGAImplementationofHodgkin-HuxleyNeuronModel

523

=(V-)

(4)

According to (Hodgkin and Huxley, 1952), the

values of activation and inactivation’s parameters

are updated by equation (5).

X (V)-X

(V)





(5)

Where

∈

{m, n, h} and

τ (V)

and

X(V)



are

obtained by (6).

τ (V) =

α (V) + β (V)

α (V)

(V) =

α (V) + β (V)



(6)

α and β ‘s equations are shown in (7).

0.01(V + 55)

(V) =

1- exp[-0.1(V + 55)]

0.1(V + 40)

(V) =

1-exp[-0.1(V +40)]

(V) = 0.07exp[-0.05(V + 65)]

(V) = 0.125exp[-0.0125(V + 65)]

(V) = 4.0exp[-0.0556(V + 65)]

(V) =

1+exp[-0.1(V +35)]

(7)

According to (Izhikevich, 2007), typical values of

maximal conductance and the membrane

capacitance are shown in equation (8).

= 36mS / cm , = 120mS / cm ,

KNa

=0.3mS/cm ,C=1μF/cm

(8)

The equilibrium potentials are shown in equation

(9).

= -54.402mV, = -77mV, = 50mV

EEE

LKNa

(9)

For digital implementation of these calculations, we

need to convert these floating point values and

computations to specific fixed point values and then

perform these computations with specific accuracy

in fixed point arithmetic. In the following section,

the details of our fixed point design and digital

implementation is expressed.

3 FPGA IMPLEMENTATION

According to the equations (1) - (7), the proposed

architecture which is implemented in this paper is

shown in figure 2. Each box corresponds to one or

more components. For implementing these

components, the required functionalities and

modules are addition, subtraction, multiplication,

division and exponential function. The main

constraint which should be considered in hardware

implementation is the parallelism and also optimal

hardware resource usage. In other words, the

implemented system should respond in real-time and

also have comparable accuracy with software

implementation. For this reason, addition and

multiplication are implemented by FPGA’s special

circuits (DSP Cores). We also designed the division

modules using shift registers and addition to save the

area.

One of the most important and critical parts of

our hardware implementation is exponential

function. The accuracy, speed and also logic

resource usage of this module has a direct impact on

the final result. For this reason we used the

hyperbolic CORDIC algorithm to estimate the

exponential function more accurately. According to

(Ercegovac and Lang, 2003), we used the following

equations in our design and implementation

(equation 10).

-j

x[j +1] = x[j] - 2 y[j]

-j

y[j + 1] = y[j] + 2 x[j]

-j

-1

z[j +1] = z[j] - tan (2 )

(10)

As shown in equation (10), shifter and adder are

needed for hardware implementation. The number of

bits used for intermediate value representation

should be selected carefully to provide the required

accuracy of the neuron. On the other hand we should

find the minimum number of bits to minimize the

FPGA resources. In other words, there is a trade-off

between accuracy and FPGA resources. We

determined the optimal representing bits for

implementation via high level simulation in

MATLAB and comparing the final results with low

level HDL simulations.

The other important part of equation (10) is

-j

-1

tan (2 )

function. It is implemented by static

ROMs or LUTs with limited rows. There exist more

accurate implementations of this function using

more hardware resources comparing the LUT

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

524



Figure 2: The proposed architecture for H-H neuron model implementation.

implementation. As we need limited accuracy, we

used LUT-based implementation to minimize the

required FPGA resources. The initial value of z[j] is

used as an argument to calculate the exponential

function. Simulation results show that 32 bit words

are enough to represent all intermediate values. As

CORDIC algorithm is defined for the limited inputs,

we separate the inputs into two parts. The most 12

significant bits are used as integer part, and the

remaining 20 bits show the fractional part of the

number. The higher 12 bits that presents the integer

part are used as LUT’s input, in which the

exponential value of this integer part is saved. In

other words, for integer numbers, the results of the

computation with adequate accuracy is computed

before, and saved in a LUT. In run-time a simple

search is performed instead of calculating its value.

As a result, the time complexity to compute this

function is O(1) and the fractional parts is given to

CORDIC algorithm. According to equation (11) the

output of the LUT and the output of the CORDIC

algorithm should be multiplied to produce the

exponential function results for 32-bit input.

θ =X+Y

exp(θ) = exp(X).exp(Y)

(11)

Based on equation (7) we use the same architecture

with different constant values to calculate α

and α

(see figure 3). The selected constant’s values used in

figure 3 are shown in Table 1.

According to equation (7), α

, β

and β

have

similar architecture which is shown in figure 4.

Table 2 shows the selective constant’s values used in

figure 4.

Table 1: Constant value for figure 3.

C1 C2 C3

55 -0.1 0.01

40 -0.1 0.1

Figure 3: α

and α

architecture.

Figure 4: α

, β

and β

architecture.

∞



Inte

rato

Inte

rato

Inte

rato

Inte

rato

FPGAImplementationofHodgkin-HuxleyNeuronModel

525

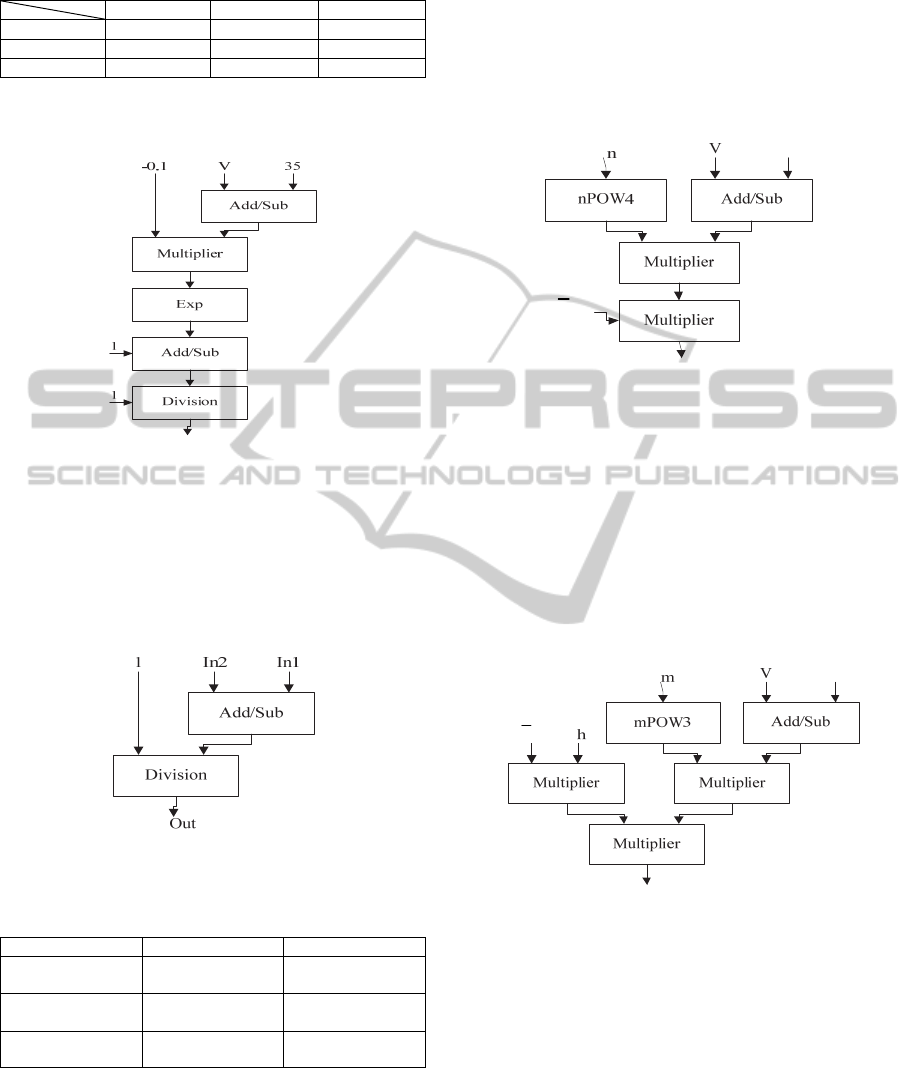
Table 2: Constant values for figure 4.

C4 C5 C6

65 -0.05 0.07

65 -0.0125 0.125

65 -0.0556 4

We used a similar architecture to calculate β

(See figure 5).

Figure 5: Proposed architecture to compute β

First of all, the results of the equation (7) have to

be computed, and the outputs should be produced.

So α

and β

are ready to be used as inputs in

equation (6). The high level implementation of

equation (6) that produces

is shown in figure 6.

Inputs and output of this module are given in Table



Figure 6: A typical implementation of



Table 3: The output and input`s values used in figure 6.

Out In1 In2



A similar architecture is used to implement X∞,

but the constant value 1 in division’s input is

replaced by the first input (In1). The outputs of these

modules which are the outputs of equation (6)

applied as inputs to equation (5). Implementation of

equation (5) is same as the architecture in figure 6,

but the first input (In1) is connected to X, and the

second input (In2) is connected to X∞ to make the

subtraction’s result and

is connected to the

division’s input which is 1 in figure 6.

The high level circuit of

implementation is

shown in figure 7.

Figure 7: The architecture of I

Another required component which is used to

calculate

is n

. This function is implemented

using three multipliers (shown as nPOW4 in figure

7).

A similar circuit is designed and implemented to

compute

. The mPOW3 (shown in figure 8)

computes m

Figure 8: The architecture of I

The last required component is I

. The

architecture of this component is shown in figure 9.

Membrane voltage in equation (1) is calculated

by the last module that is an adder with four inputs,

called I

, I

and I

ext

. Input I

ext

is an external

current that stimulates the neuron.

The new values of the n, m, h and V are

calculated using integrators with



and



inputs, respectively. To implement the integrator,

equation (12) is used by step time of 0.01 ms. This

step time is selected based on our design and also

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

526

our evaluation board which is used for prototyping.

Figure 9: The architecture of I

X(t + Δt) = X(t) + Δt*X(t)



(12)

Equation (12) is implemented using a simple MAC

(multiply and accumulate) and rounded to 32 bits. In

the following section, the experimental setup,

validation and evaluation of the proposed

architecture is described.

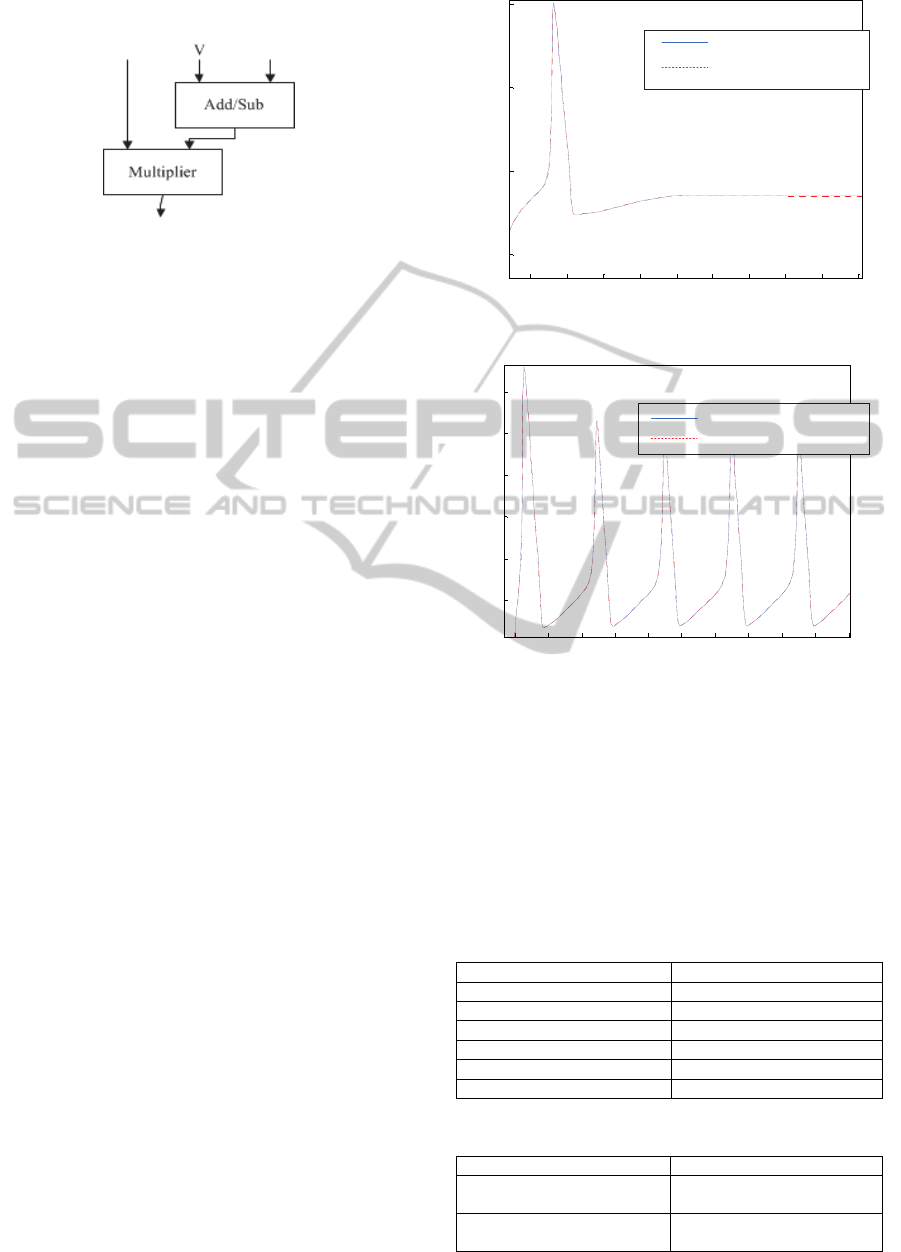
4 RESULTS

To validate the FPGA implementation results, the

implemented bit level simulation is compared with

MATLAB simulation system. For high level

simulation we use Simulink, and all hardware

components are designed and implemented using

VHDL modelling language. The main design

objective of the low level implementation is the

output accuracy. Due to the implementation

constraints, we should use the minimum number of

bits in all module implementations. The details of

implementation are given in Tables 4 and 5. We

tested the behavior of both systems for different

values of parameters, initial values, and external

currents. Here, the results for two important cases

are shown; i) no stimulation is applied (I

ext

= 0), and

the neuron goes to the rest state after a transition

time (Figure 10), ii) a strong stimulation (I

ext

30mA) is applied, and thus the neuron exhibits

periodic (tonic) spiking (Figure 11). In figure 10,

and 11, the membrane voltage (V) of the neuron

from MATLAB simulation (solid blue line), and

from FPGA implementation (dashed red line) is

shown. There are only very little differences

between the two waveforms, which are due to the

rounding error, due to the limitation of the number

of bits to 32 in FPGA implementation. This error is

in an acceptable range, and can be reduced, by

extending this number representation system.

5 10 15 20 25 30 35 40 45 50

-100

-50

Time(ms )

Voltage(mV)

Figure 10: Membrane voltage of neuron for I

ext

=0mA.

0 5 10 15 20 25 30 35 40 45 50

-60

-40

-20

Time(ms )

Voltage(mV)

Figure 11: Membrane voltage of neuron for Iext=30mA.

We implemented the neuron on a Xilinx FPGA

(Spartan3). The resource usages and critical path

delay are reported in Table 4 and Table 5. According

to the reported experimental results we are able to

implement one neuron in a Spartan FPGA working

with frequency of 37.563MHz. Also we can use

larger devices to implement more neurons in one

device.

Table 4: Device utilization summary.

Number of Slices 13273 out of 23872

Number of Slice FFs 7231 out of 47744

Number of 4 input LUTs 23514 out of 47744

Number of IOs 292

Number of bonded IOBs 292 out of 469

Number of GCLKs 24 out of 24

Number of DSP48s 99 out of 126

Table 5: Timing summary.

Minimum period 26.622ns

Minimum input arrival time

before clock

10.982ns

Maximum output required

time after clock

6.068ns

MATLAB simulation

FPGA implementation

MATLAB simulation

FPGA im

lementation

FPGAImplementationofHodgkin-HuxleyNeuronModel

527

5 CONCLUSIONS AND FUTURE

WORKS

In this paper the Hodgkin-Huxley model of a single

biological neuron has been designed and

implemented on an FPGA. Unlike previous

approaches, we used the CORDIC algorithm for

implementing the exponential functions and other

arithmetic parts. So our used logic is more compact

than previous ones. The accuracy and performance

of our proposed approach is validated by MATALB

high level implementation. Because of establishing

trade-off between used area and frequency, the

number (and also format) of representing bits of our

arithmetic parts were selected carefully and

validated and verified by high level simulation. For

instance, it was shown that the neuron spiking

frequencies in MATLAB simulation and in FPGA

implementation almost are the same. It is a very

important parameter because it codes the

information that a neuron transmits. The hierarchal

proposed design and implementation allows simple

modification of it to an equivalent small pipeline

system, which is useful in implementing a large

neural network. We plan to optimize our hardware to

make it smaller and finding the optimal bit length of

each parameter separately. Moreover, the behaviour

of the implemented neuron will be benchmarked

against the behaviour of a natural one. Furthermore,

implementing a neural network of competing

minicolumns (Bakhtiari. et al., 2012) in FPGA is the

next target of this research.

REFERENCES

Bakhtiari, R., Sepahvand, N. M., Ahmadabadi, M. N.,

Araabi, B. N., Esteky, H., 2012. Computational model

of excitatory/inhibitory ratio imbalance role in

attention deficit disorders. Computational

Neuroscience.

Ercegovac, M. D., Lang, T., 2003. Digital Arithmetic, 1st

ed. Morgan Kaufmann.

Gatet, L., Tap-Béteille, H., Bony, F., 2009. Comparison

between analog and digital neural network

implementations for range-finding applications.

Neural Networks, IEEE Transactions on 20, 460–470.

Graas, E. L., Brown, E. A., Lee, R. H., 2004. An FPGA-

based approach to high-speed simulation of

conductance-based neuron models. Neuroinformatics

2, 417–435.

Hodgkin, A. L., Huxley, A. F., 1952. A quantitative

description of membrane current and its application to

conduction and excitation in nerve. J. Physiol. (Lond.)

117, 500–544.

Izhikevich, E. M., 2007. Dynamical systems in

neuroscience: the geometry of excitability and

bursting. MIT Press.

Kandel, E. R., Schwartz, J. H., Jessell, T. M., others, 2000.

Principles of neural science. McGraw-Hill New York.

Li, G., Talebi, V., Yoonessi, A., Baker, C. L., Jr, 2010. A

FPGA real-time model of single and multiple visual

cortex neurons. J. Neurosci. Methods 193, 62–66.

Mokhtar, M., Halliday, D. M., Tyrrell, A. M., 2008.

Hippocampus-Inspired Spiking Neural Network on

FPGA, in: Proceedings of the 8th International

Conference on Evolvable Systems: From Biology to

Hardware, ICES ’08. Springer-Verlag, Berlin,

Heidelberg, pp. 362–371.

Muthuramalingam, A., Himavathi, S., Srinivasan, E.,

2008. Neural network implementation using FPGA:

Issues and application. International journal of

information technology 4, 86–92.

Pourhaj, P., Teng, D.H.., 2010. FPGA based pipelined

architecture for action potential simulation in

biological neural systems, in: Electrical and Computer

Engineering (CCECE), 2010 23rd Canadian

Conference On. pp. 1–4.

Rice, K. L., Bhuiyan, M. A., Taha, T. M., Vutsinas, C. N.,

Smith, M.C., 2009. FPGA implementation of

Izhikevich spiking neural networks for character

recognition, in: Reconfigurable Computing and

FPGAs, 2009. ReConFig’09. International Conference

On. pp. 451–456.

Wanhammar, L., 1999. DSP integrated circuits. Academic

Press.

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

528