A New Metaheuristic for Float Management in Resource-constrained

Project Scheduling

A Bi-criteria Approach

Roni Levi

and Sándor Danka

Technion Israeli Institute of Technology, Haifa, Israel

University of Pécs, Pécs, Hungary

Keywords: Project Scheduling, Resource-constrained Project, Resource-constrained Float, Heuristic Algorithm, Project

Management.

Abstract: In this paper, we present a new unified theoretical model and the conception of the corresponding heuristic

algorithm to solve several "what if" like float management problems in resource-constrained project

scheduling. The traditional time-oriented resource-constrained project scheduling model for makespan

minimization gives an optimal starting time set therefore an activity movement, may be able to destroy the

resource-feasibility. The float management, as a stating base, needs a so-called forbidden-set oriented model

(a forbidden-set oriented heuristic), which gives an optimal resource conflict repairing relation set. After

inserting the additional predecessor-successor relations, in a optimal schedule every movable activity can be

moved without destroying the resource feasibility. In the other side, when we have a forbidden-set oriented

schedule, then according to the total free float, we have some freedom to redistribute the float among

activities to answer several "what if" like questions. For example, in the planning phase we can investigate

the consequences of a delay or a longer duration which may be caused by a notorious element of the

"critical" activity subset. The unified float management as a new tool was built into the forbidden-set

oriented Sounds of Silence (SoS) metaheuristic frame (Csébfalvi et al., 2008a). From theoretical point of

view, float management is invariant to the applied heuristic frame; therefore it can be built into any other

heuristic which is developed to solve forbidden-set oriented resource-constrained project scheduling

problem (RCPSP). The toolbox can be completed by any other new element (float measure), which can be

described as a linear programming (LP) or a simple mixed integer linear programming (MILP) problem on

the set of the forbidden-set oriented (freely movable without resource-conflicts) solutions as a problem-

specific redistribution of the total free float of the project. The essence and viability of our unified approach

is illustrated by a set of examples.

1 INTRODUCTION

Critical path has long been central to the analysis of

non-resource constrained projects. This issue

becomes more crucial when resource constraints are

introduced. Even in simple resource constrained

projects, alternative resource allocations are often

possible, resulting in a choice of schedules with

identical project durations, but different critical

sequences. An activity may be critical in one

schedule, but have considerable float (flexibility) in

another. In such situations an analysis of floats plays

an important and crucial role, making the

development of new float measures a central issue in

project scheduling.

The desirability of additional float measures has

been noted in reviews of project scheduling

literature conducted by and Ragsdale (1989). As part

of this endeavor, Weist (1967) proposed the "critical

sequence" as an extension of the critical path. This

concept was employed by Bowers (1995) in the

development of a set of heuristics for determining a

resource constrained float. Raz and Marshall (1996)

explored a definition of resource constrained float

involving the generation of two different schedules.

Bowers (2000) proposed a float definition for

multiple alternative resource constrained schedules.

In a previous study (Levi, 2004) we presented a

resource constrained total project float model to for

this problem, where the resource constrained total

290

Levi R. and Danka S..

A New Metaheuristic for Float Management in Resource-constrained Project Scheduling - A Bi-criteria Approach.

DOI: 10.5220/0004152702900293

In Proceedings of the 4th International Joint Conference on Computational Intelligence (ECTA-2012), pages 290-293

ISBN: 978-989-8565-33-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

project float measure (RCTPF) was defined as the

sum of the activity floats. In the proposed primary-

secondary criteria approach, we maximized the

RCTPF value on the set of makespan minimal

resource-constrained schedules.

Theoretically, the optimal schedule searching

process was formulated as a mixed integer linear

programming (MILP) problem, which can be solved

for small-scale projects in reasonable time. A

conflict repairing harmony search metaheuristic for

the proposed primary-secondary criteria approach

was presented by Csébfalvi et al. (2008b).

The RCTPF is in essence a flexibility measure

which is geared toward enhancing the schedule

robustness by maximizing the project total float. The

greater the RCTPF is, the better the solution (the

robustness) is.

In this paper, we argue that not only the

existence of float or its amount is important, but in

many cases the distribution of the total amount of

the float within the activities is even more

significant.

In the recent study, we introduce a model family

connected directly or indirectly to the RCTPF,

which can be a useful to cope with the several "what

if" like questions.

In the proposed bi-criteria approach, a resource-

feasible schedule is characterized by the project

makespan and the current value of the selected float

measure from the measure family. In the presented

bi-criteria approach it is characterized by its Pareto

front. We have to note, that there is a "natural"

conflict between these performance measures

(makespan - float) because the longer the "playfield"

the higher the chance that we are able to reach a

good float measure value and vice-versa.

The theoretical model will be shown is Section 2.

In Section 3 we summarise the most important

elements of the heuristic algorithm which is based

on the resource conflict repairing version of Sounds

of Silence (SoS) harmony search heuristic developed

by Csébfalvi et al. (2008b) and Csébfalvi and Láng

(2011). In Section 4 we present some motivating

examples. Finally, Section 5 draws conclusions from

this study.

2 THEORETICAL MODEL

The core element of the forbidden-set oriented

mathematical model which is able to handle float

management problems is very simple. It is a

straightforward modification of the conflict repairing

model developed by Alvarez-Valdés and Tamarit

(1993) omitting unnecessary elements, replacing the

starting time variable with an early (late) starting

variable for each real activity, and rewriting the

original network and the potential conflict repairing

relations according to the early (late) starting time

variables. The free float is defined as the amount of

time that an activity can slip without delaying the

start of its successors and while maintaining

resource feasibility. The resource constrained total

free float measure (RC-TFF) is defined as the sum of

the free floats of activities.

The developed resource-constrained float model

family consists of the following approaches:

 Total free float (RC-TFF) maximization for a

given resource-feasible makespan (RC-MS).

 Uniform free float redistribution (RC-UFF)

according to the given RC-MS and RC-TFF.

 Maximization the cardinality of the floatable

(shiftable) activities (RC-CFF) for a given RC-MS.

 Makespan minimization subject to the desired

activity floats (RC-PFF) for a given "critical"

activity subset.

3 HEURISTIC APPROACH

Harmony Search (HS) algorithm was recently

developed by Lee and Geem (2005) in an analogy

with music improvisation process to obtain better

harmony. In the HS algorithm, the optimization

problem is specified as follows:

Max{ f(X) | { X | X

≤ X ≤ X

} } (1)

In the language of music, vector X is a melody,

which aesthetic value is represented by f(X). In the

band, the number of musicians is N, (X=[X

, X

, … ,

], and musician i, is responsible for sound X

. The

improvisation is driven by two parameters. (1)

Repertoire consideration rate (RCR): each musician

is choosing a sound from his/her repertoire with

probability RCR, or a totally random value with

probability (1-RCR). (2) Sound adjusting rate

(SAR): the sound, selected from his/her repertoire,

will be modified with probability SAR. The

algorithm starts with a totally random “repertoire

upload” phase, followed by improvisations. During

the improvisations, when a new melody is better

than the worst in the repertoire, it will be replaced by

the better one. The two most important parameters

of HS algorithm are the repertoire size and the

number of improvisations. The HS algorithm is an

“explicit” one, because it operates directly on the

sounds. In the case of RCPSP, we can only define an

ANewMetaheuristicforFloatManagementinResource-constrainedProjectScheduling-ABi-criteriaApproach

291

“implicit” algorithm, and without introducing a

“conductor” we can not manage the problem

efficiently.

First, we show how the original problem can be

transformed into the world of music. Here, the

resource profiles form a “polyphonic melody”. So,

assuming that in every phrase only the “high

sounds” are audible, the transformed problem will

be the following: find the shortest “Sounds of

Silence” melody by improvisation! Naturally, the

“high sound” in music is analogous to the overload

in scheduling.

In the harmony searching process, the

improvisation is fundamentally driven by the “ideas

of the musicians”, but each of the possible decisions

is made by the conductor (hierarchy is hierarchy). At

the start of an improvisation step, the conductor

selects a “promising” melody from the repertoire or

leaves the musicians to improvise freely. In our

magic world, the task of the musicians is very

simple: they only have a slider to select (modify) a

value from interval [-1, 1]. A large positive

(negative) value means that the musician wants to

enter into the melody as early (late) as possible..

Naturally, the magic conductor is able to resolve the

possible conflicts between the fighting ideas and

define the final entering order for the musicians by

solving very simple linear programming problem

which gives a scheduling order. If, the new melody

“sounds good” (it is shorter than the longest “Sounds

of Silence” melody in the repertoire) than it will be

memorized.

The forbidden set can be defined as a set of

activities that could be scheduled concurrently, and

if activities of the set scheduled in parallel, they

would violate the resource constraints. To resolve

the resource conflicts caused by minimal forbidden

sets, it needs to introduce explicit resource conflict

repairing relationships. It is important to note that

the introduction of an explicit conflict repairing

relation might resolve (correct) more than one

forbidden set implicitly.

In the traditional time-oriented model, according

to the explicit resource conflict handling an activity

shift might destroy the schedule. In the presented

model the resource feasibility is not affected by the

feasible activity moves, because of the implicit

resource conflict handling.

In the SoS algorithm, the conductor uses a

simple (but fast and effective) “thumb rule” to

decrease the time requirement of the forbidden set

computation:

 In the forward-backward list scheduling process

the conductor (without explicit forbidden set

computation) inserts a precedence relation i→j

between an already scheduled activity i and the

currently scheduled activity j whenever they are

connected without lag. The result will be schedule

without “visible” conflicts.

 After that, the conductor (in exactly one step)

repairs all of the hidden (invisible) conflicts,

inserting always the “best” conflict repairing relation

for each forbidden set. In this context “best” means a

relation i→j between two forbidden set members for

which the lag is maximal.

The result of the conflict repairing process will be a

resource-feasible solution set, in which every

movable activity can be shifted without affecting the

resource feasibility. It is well-known that the crucial

point of conflict repairing model is the forbidden set

computation. In the improved algorithm we

combined the "hidden conflict repairing step" with a

pre-processing step to decrease the time requirement

of the forbidden set computation and to speed up the

problem solving process. The essence of the pre-

processing step is very simple: In a cyclically

repairable process, we select the incompatible

activity pairs (triplets) which have exactly one

conflict repairing relation and insert the precedence

relations. The process is terminated when the

relation set will be empty (Csébfalvi and Szendrői,

2012).

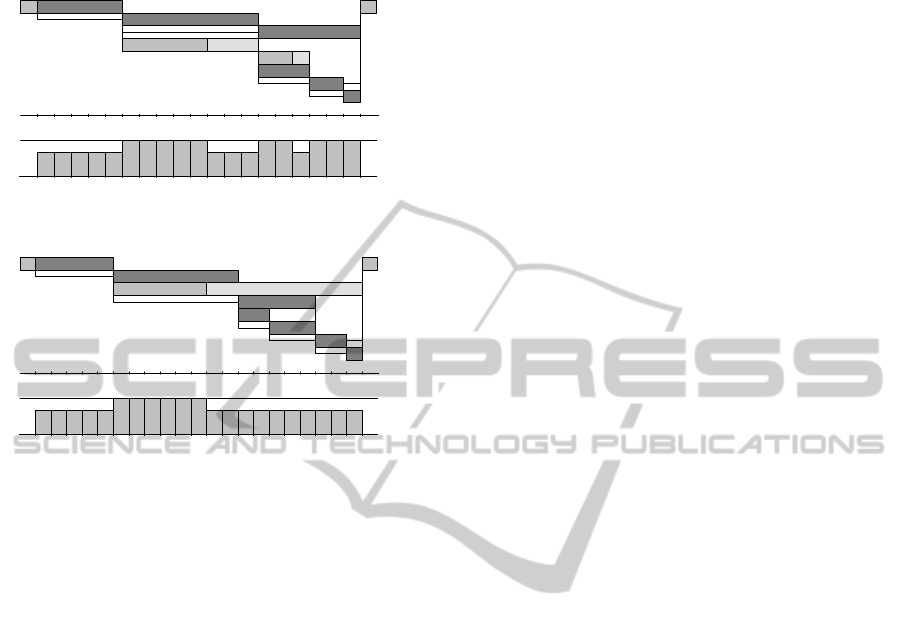
4 MOTIVATING EXAMPLES

In this section we show the answers for two "what

if" like questions for a very simple project with one

resource and eight real activities, to demonstrate its

usefulness. Figure 1 shows the makespan minimal

solution with "distributed" floats. Dark grey

background colour means critical activity, the lighter

grey means "freely movable" activity, and light grey

describes its "playfield". When we assume that our

uncertainty about the real duration of activity 3 is

large enough (it is a notorious one) then it would be

good to know, how we can schedule activity 3 more

safely in the price of a two periods longer project

makespan (in the makespan minimal solution,

activity 3 is critical, so from the project manager

point of view, the schedule is a terrible bad

nightmare). In Figure 2 we show the "conformist"

solution.

In each case, SoS reached the optimal solution

very quickly, using a repertoire consisting of only

ten melodies. The number improvisation cycles was

also ten (a cycle means repertoire size

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

292

improvisations). We run SoS, in each case, with

"frozen" golden numbers (tunable parameters).

0 1

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

Figure 1: A makespan minimal solution.

0 1

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1

18 19 20 21

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

Figure 2: A "conformist" solution for activity 3.

5 CONCLUSIONS

In this paper, a new unified theoretical model and

the conception of the corresponding heuristic

algorithm were presented to solve "what if" like float

management problems in RCPSP. The unified float

management as a new tool was built into the SoS

metaheuristic frame. From theoretical point of view,

the float management is invariant to the applied

heuristic frame; therefore it can be built into any

other heuristic which is developed to solve

forbidden-set oriented RCPSP. The toolbox can be

complete by any new element (float measure), which

can be described as an LP on the set of the

forbidden-set oriented solutions as a problem-

specific redistribution of the total free float. The

essence and viability of our unified approach was

illustrated by simple motivating examples. The test

of the new float-oriented elements of SoS is under

progress using the J30 subset of PSPLIB (Kolisch

and Sprecher, 1996) varying the maximal allowed

makespan increase. The algorithm was programmed

in Compaq Visual FORTRAN 6.5. To solve the

benchmark problems to optimality, as a MILP

solver, the callable version of Cplex 12.2 was used.

The benchmark results for J30 will be presented in a

forthcoming paper.

REFERENCES

Alvarez-Valdés, R., Tamarit, J. M., 1993. The project

scheduling polyhedron: Dimension, facts and lifting

theorems, European Journal of Operational Research,

96, 204-220.

Bowers, J. A., 1995. Criticality in Resource Constrained

Networks, Journal of Operational Research Society,

46, 80-91.

Bowers, J. A., 2000. Interpreting Float in Resource

Constrained Projects, International Journal of Project

Management, 18, 385-392.

Csébfalvi A., Láng, B., 2011. An improved hybrid method

for the resource-constrained project scheduling

problem with discounted cash flows. Pollack

Periodica: An International Journal For Engineering

and Information Sciences, 6 (3), 1-12.

Csébfalvi, A., Szendrői, E., 2012. An improved hybrid

method for the multi-mode resource-constrained

project scheduling problem. In Tooping, B.H.V. (Ed.),

Proceedings of the Eight International Conference on

Engineering Computational Technology, (ECT

2012/00036).

Csébfalvi, G., Eliezer, O., Láng, B., Levi, R., 2008a. A

conflict repairing harmony search metaheuristic and its

application for bi-objective resource-constrained

project scheduling problems, Project Management and

Scheduling 2008, Istanbul, Turkey, 60-63, 2008.

Csébfalvi, G., Csébfalvi, A., Szendrői, E., 2008b. A

harmony search metaheuristic for the resource-

constrained project scheduling problem and its multi-

mode version, Project Management and Scheduling

2008, Istanbul, Turkey, 56-59.

Kolisch, R., Sprecher, A., 1996. PSPLIB – a project

scheduling library. European Journal of Operational

Research, 96, 205-216.

Lee K. S., Geem Z. W., 2005. A new meta-heuristic

algorithm for continuous engineering optimization:

harmony search theory and practice, Computer

Methods in Applied Mechanics and Engineering, 194,

3902-3933

Levi, R., 2004. Criticality in Resource Constrained

Projects, PhD Dissertation, University of Pécs,

Hungary.

Ragsdale, C., 1989. The Current State of Network

Simulation in Project Theory and Practice, Omega, 17,

21-25.

Raz, T., Marshall, B., 1996. Effect of Resource

Constraints on Float Calculation in Project Networks,

International Journal of Project Management, 14,

241-248.

Weist, J. D., 1967. Heuristic Model for Scheduling Large

Projects with Limited Resources, Management

Science, 13, 359-377.

ANewMetaheuristicforFloatManagementinResource-constrainedProjectScheduling-ABi-criteriaApproach

293