
The Brain in a Box
An Encoding Scheme for Natural Neural Networks
Martin Pyka
1
, Tilo Kircher
1
, Sascha Hauke
2
and Dominik Heider
3
1
Section BrainImaging, Department of Psychiatry, University of Marburg, Marburg, Germany
2
Telecooperation Group, Technische Universit
¨
at Darmstadt, Darmstadt, Germany
3
Department of Bioinformatics, University of Duisburg-Essen, Duisburg and Essen, Germany
Keywords:
Neural Networks, Artificial Development, CPPN.
Abstract:
To study the evolution of complex nervous systems through artificial development, an encoding scheme for
modeling networks is needed that reflects intrinsic properties similiar to natural encodings. Like the ge-
netic code, a description language for simulations should indirectly encode networks, be stable but adaptable
through evolution and should encode functions of neural networks through architectural design as well as sin-
gle neuron configurations. We propose an indirect encoding scheme based on Compositional Pattern Produc-
ing Networks (CPPNs) to fulfill these needs. The encoding scheme uses CPPNs to generate multidimensional
patterns that represent the analog to protein distributions in the development of organisms. These patterns
form the template for three-dimensional neural networks, in which dendrite- and axon cones are placed in
space to determine the actual connections in a spiking neural network simulation.
1 INTRODUCTION
If evolutionary development, i.e., the stepwise im-
provement through mutation and crossover, is seen as
a means of understanding natural networks, two open
questions in particular present themselves. First, how
must a description language for neural networks (e.g.
complex nervous systems) look like? And second,
what are appropriate fitness functions to evolve com-
plex networks? In this article, we propose an answer
to the first question.
Because such a description language has to be ca-
pable of developing natural neural networks, it is im-
perative to know the intrinsic properties of the net-
works that should be modeled. In neuroscientific dis-
ciplines, numerous properties of natural neural net-
works are well-accepted that, in our opinion, should
receive considerably more attention in those disci-
plines that try to model networks by evolutionary
means.
For instance, the cortex of the brain consists of
layers of different neuron types interconnected with
each other. The connections are a side-effect of the
position of the neurons within the layer, their anatom-
ical form and their intersection with other neurons
(Wolpert, 2001). Connections between neurons can
be either specific (a clear and precise determination
of connections, e.g. as it can be found in the thalamus
(Basso et al., 2005)) or driven by side effects (e.g.
adjacent regions are interconnected with each other).
Furthermore, the (genetic) encoding scheme for
natural organisms itself has certain properties that
should be considered in simulations. In biological
organisms, comparatively few genes (e.g., the hu-
man genome consists of circa 22,000 genes) encode
complex structures by using highly indirect mecha-
nisms. The encoding involves local interactions be-
tween cells, diffusion of substrates and gene regu-
latory networks. One purpose of these mechanisms
is to generate global patterns from local interactions
between genes that serve as axes for the organiza-
tion and refinement of (cellular) structures (Mein-
hardt, 2008; Raff, 1996; Curtis et al., 1995). From this
notion, it can be concluded that an encoding scheme
for the evolutionary exploration of neural networks
should work in a highly indirect manner as well and
serve as a pattern generator for subsequent structural
elements. If the network architectures should be im-
provable via evolutionary mechanisms, the encoding
scheme must fulfill requirements for generating stable
network architectures across generations, but should
also facilitate alterations in the network that can im-
pact (and improve) their functionality.
In the following, we propose an encoding scheme,
196
Pyka M., Kircher T., Hauke S. and Heider D..
The Brain in a Box - An Encoding Scheme for Natural Neural Networks.
DOI: 10.5220/0004152801960201
In Proceedings of the 4th International Joint Conference on Computational Intelligence (ECTA-2012), pages 196-201
ISBN: 978-989-8565-33-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

which we call Brain In a Box (BIB), that aims to gen-
erate networks with the outlined properties via pattern
generation. It comprises three steps which will be de-
scribed in detail in the following sections: i) Generate
global patterns of protein densities, representing po-
tential neuron locations and their properties; ii) Con-
vert these patterns into a 3D-representation of neurons
where axon- and dendrite-cones are used to determine
connections between neurons; iii) Run a neural net-
work simulation using the inferred network configura-
tion. We think, that this encoding scheme is not only
useful in the evolutionary exploration of network ar-
chitectures, but can also serve as a model to describe
real neural networks.
2 STEP 1: GLOBAL PATTERN
GENERATION
In a BIB, network architectures are inferred from neu-
rons placed in a three-dimensional space. Each neu-
ron can be characterized by several properties im-
pacting their potential connections to other neurons.
These properties include, for instance, its position and
its orientation in space. Potential axons and dendrites
are indicated through cones projecting away from the
neuron (Fig. 4). The length of the cone and its width
(defined by its angle) determine a volume that may
intersect with cones of other neurons. In case of an
intersection, a density parameter of the neuron deter-
mines the chance for a potential connection. In a bi-
ological sense, different types of proteins form – de-
pending on its concentration, location and combina-
tion with other proteins – the structure of a neuron.
Connections between neurons are just a subsequent,
probabilistic side-effect of their properties and place-
ment in space.
BIBs are generated by mapping the three space co-
ordinates, a distance and a bias value to several output
values, representing the above mentioned properties
of the neuron (Fig. 1). The mapping is computed by
Compositional Pattern Producing Networks (CPPNs)
which model how gene regulatory networks (GRNs)
generate global patterns, while exploiting computa-
tional shortcuts in the simulated world (Stanley, 2007)
(Fig. 2). An additional output node encodes whether
a neuron is built at a given location. Intermediate
genes are activated either by the (initial) input values
or by other genes and generate density distributions
that modulate, for instance, axon length and orienta-
tion of the neuron. Thus, a single gene may have a
modulating influence on either one or several prop-
erties of neurons. This means, the functional role of
neurons is controlled by genes influencing the struc-
x y z d b
n nx ny nz aa al ad da dl dd
Compositional Pattern Producing Network
normal vector axon parameter dendrite parameterneuron
Figure 1: Structure of a CPPN for a BIB. The axes of the
three-dimensional space (x, y, z) a bias value (b) and a dis-
tance value indicating the distance for a given point to the
center of the volume (d (Stanley, 2007)), are mapped via a
CPPN (see also fig. 2) on various parameters of the neu-
ron. The output values encode, whether a neuron should be
placed (n), the orientation of the neuron (nx, ny, nz), and
the angle, length and density of the axon and dendrite cones
(aa, al, ad, da, dl, dd).
tural properties of the neurons.
x y z
Figure 2: Example of a Compositional Pattern Producing
Network. Global axes serve as input for concatenated func-
tions generating two- or three-dimensional patterns. The
functions represent the analog to density distributions of
genes which activate other genes.
TheBraininaBox-AnEncodingSchemeforNaturalNeuralNetworks
197

Figure 3: 3D-representation of a neural network using a res-
olution of 20 × 20 × 20 neurons. For clarity’s sake, cones
for axon and dendrite connections are not displayed. In the
lower left corner, the volume generated by the CPPN is de-
picted in a higher resolution.
3 STEP 2: CONVERSION OF THE
NETWORK INTO 3D
The patterns generated in the previous step are used
to generate a 3D-representation of the neural network
(fig. 3). Only at this stage, it is necessary to spec-
ify the spatial resolution in which the neural network
should be generated. A routine calls the CPPN with
all coordinate values in the given resolution and deter-
mines, whether or not a neuron should be placed at a
given location, and if yes, which properties the axon-
and dendrite cones have (Fig. 4). If axon- and den-
drite cones intersect, density parameters of the cones
provided by the CPPN (ranging from 0.0 to 1.0) are
multiplied and used as probability for a directed con-
nection generated between both neurons.
Since BIBs can also be used to model real (bio-
logical) neural systems, such as cortex layers, the 3D-
representation provides a means to obtain face valid-
ity upon a given anatomical structure. Here, again the
role of genes within the model can be characterized
and validated against the potential role of biological
candidate genes.
4 STEP 3: SPIKING NEURAL
NETWORK SIMULATION
The network information obtained from the pre-
vious step can subsequently be used in any type
of neural network simulations to simulate and test
Figure 4: Three-dimensional representation of a neuron. A
neuron is characterized by its location in space, its orienta-
tion and some parameters describing the cones for potential
axons and dendrites. The green cone represents potential
axon-connections and the blue cone potential dendrite con-
nections.
the network. In our BIB-code, we chose Brian
(www.briansimulator.org, (Goodman and Brette,
2008)) as framework for implementing a spiking neu-
ral network system. For each 3D-neuron generated
in the second step, a neuron was generated in Brian
and connected with other neurons as determined in
the 3D-representation. The time-course of each neu-
ron was defined as
dV
dt
=
−(V − E
L
)
τ
, (1)
where V is the activity of a neuron for a certain point
t in time. E
L
can be regarded as an attractor or resting
state of the neuron and τ is a time-scaling factor. If
V exceeds a threshold V
t
, the neuron sends a spike
through the axon and V is set to a reset-level V
r
, from
which it approximates E
L
as described in Eq. (1).
5 SIMULATION
In the following, we will demonstrate that BIBs might
be a valuable framework for two purposes: On the
one hand, BIBs can be used to develop networks
with evolutionary means. This implies, however, a
well-defined fitness-function that reflects somehow
the function of a dedicated region in a brain. On the
other hand, BIBs can be used as a model to imitate bi-
ological relationships between genotype and pheno-
type of brain structures.
Having said this, we argue that, in principle, con-
troller networks can be evolved and BIBs can gener-
ate networks, in which groups of neurons on different
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
198

scales can be altered in a semantical meaningful man-
ner.
5.1 Proof of Principle
In a first test, we show that the evolutionary algo-
rithm implemented in NeuroEvolution of Augment-
ing Topologies (NEAT) (Stanley, 2002) also works for
BIBs. This is achieved via a simulation, in which an
organism, controlled by a network of sensors, neurons
and motors, can navigate on a 2D-plane with different
concentrations of a notional substrate called “feed”.
The plane is represented by a 10x10 raster, in which
the center of each field has a different concentration
of the substrate. The “feed” concentration of any in-
termediate point in the continuous space is the inter-
polated value of the four adjacent centers (Fig. 5a).
The fitness value of the organism increases by har-
vesting the “feed” of the raster field on which it is lo-
cated. At the same time, the “feed” volume decreases
on the field when it is harvested. Thus, the organ-
ism has to move to other fields in order to “consume”
more “feed”. Additionally, the fitness of the organism
is decreased by the number of neurons (divided by
100). Thus, a solution with less neurons is regarded
as more efficient.
To interact with the environment, we amended the
BIB-model by sensors and motors, which represent
special types of neurons. Sensors are able to measure
the “feed”-concentration at their location. Motor neu-
rons can generate an impulse for a movement. The
direction of the movement is determined by the rela-
tive direction between the center of the neural net and
the position of the motor neuron in the network. As
we used spiking neurons for the transition of informa-
tion, the “feed” concentration was converted into a se-
quence of spikes originating from the sensor neurons.
A higher concentration of “feed” leads to a higher fir-
ing rate. Likewise, a higher firing rate of a motor neu-
ron generates a stronger impulse for a movement into
a certain direction. The CPPN of a BIB was extended
by two output nodes encoding the existence of sen-
sor and motor neurons for a given location. A BIB,
converted to a neural network, was simulated for 5
seconds (simulation time) in intervals of 250ms.
The evolutionary algorithm of NEAT was used to
improve the network configuration. 100 individuals
per generation were tested and the four best individu-
als of each species were used to create the next gener-
ation. Crossover was always applied in order to gen-
erate a new genome. New genes were added with a
probability of 0.1, new connections between genes
with a probability of 0.2 and continuous changes
of the connection weights with a probability of 0.2.
Figure 5: Some elements of the simulation. a) The organ-
ism moves on a 2D-plane with different concentrations of
a fictive substrate called “feed”. The concentration of any
point on this plane is the interpolated value of the centers
of each field. b) The frequency of a spiking motor neuron
determines the strength of a movement impulse towards its
direction. The cumulated sum of movement impulses is the
direction in which the organism moves.
Three-dimensional networks were created with a res-
olution of five neurons per axis.
The whole evolutionary search was repeated ten
times. In all runs, networks were found in which sen-
sors forwarded information to motor neurons in or-
der to move the organisms towards higher concentra-
tions of “feed”. In some solutions, normal neurons
were completely avoided to transport sensory infor-
mation to the motor neurons. Figure 6 shows some
of the networks that have been generated. The evo-
lutionary search revealed that those BIBs that have
wider axon cones in order to reach more motor neu-
rons, show increased fitness because they can move
faster towards higher concentrations of “feed”. This
example provides evidence that changes in the BIB
can lead to abstract alterations in the neural model
(such as axon cone width) that can influence the fit-
ness of the model.
As the network is generated from a CPPN,
changes in the expression intensity of a gene can
have a global influence on the anatomy of the net-
work, when they are directly or indirectly (via gene-
TheBraininaBox-AnEncodingSchemeforNaturalNeuralNetworks
199
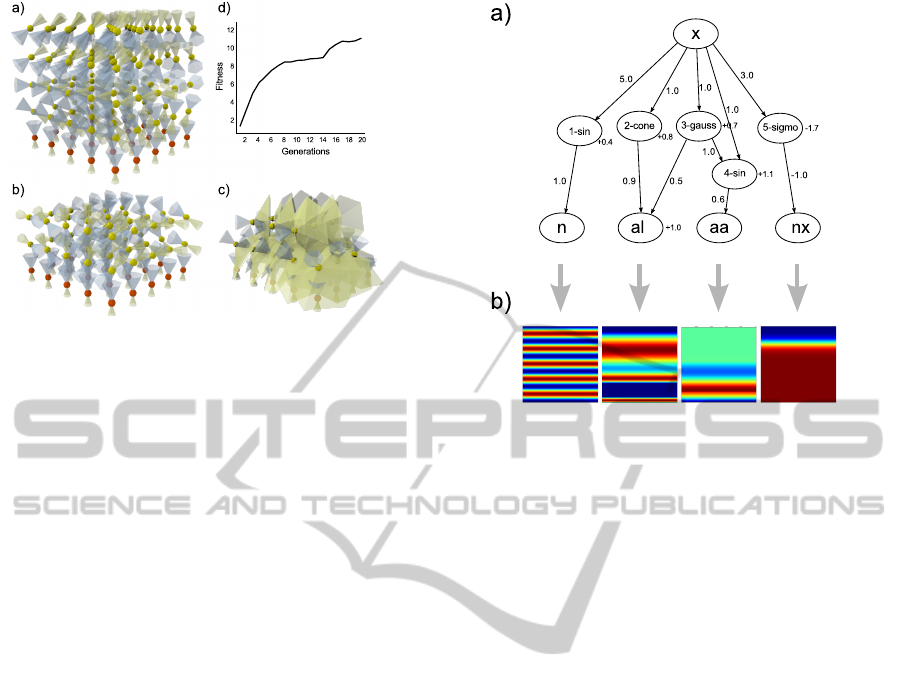
Figure 6: Some networks generated by the evolutionary
search for BIBs. Yellow spheres represent sensor neurons,
red spheres represent motor neurons. Cones indicate axon-
and dendrite areas of the neurons. a) One of the first net-
works, that successfully controlled the organism towards
more “feed”. b) and c) are more sophisticated versions of a)
with less neurons and wider axon-cones leading to a faster
movement of the organism and less energy consumption. d)
depicts the averaged fitness for one run over 20 generations.
interactions) involved in the activation of certain neu-
ral parameters. However, continuous changes of
gene-values cause continuous changes in the net-
work architecture. Thus, an evolution-driven search
can gradually improve fitness by altering the weights
of the cis-regulatory elements. New genes or cis-
elements can have a stronger influence of the network
architecture leading to new innovations.
5.2 BIBs as a Model for Complex
Nervous Systems
A BIB does not model a developmental growth pro-
cess in terms of local interactions, cell division or cell
movement but encodes the properties of a given lo-
cation directly. However, this does not mean that a
BIB does not reflect the outcome of a growth process.
As already argued for CPPNs (Stanley, 2007), genes
and their corresponding proteins are involved in a cas-
cade of local interactions and diffusion processes that
generate gradients of various protein concentrations
(Meinhardt, 2008; Raff, 1996; Curtis et al., 1995).
These gradients serve as local axes for subsequent lo-
cal reactions with other genes. From this perspective,
genes, not directly involved in building structural ele-
ments, can be regarded as density functions activating
or inhibiting other genes and thereby facilitating coor-
dination on various spatial scales. Therefore, CPPNs
(and BIBs) implicitly model the chronology of devel-
opmental events and cell interactions by concatenat-
ing functions with each other as depicted in Fig. 2.
Figure 7: BIB as model for cortical layers. a) A CPPN
with five genes generates patterns along the x-axis for cer-
tain properties of the neurons. b) 2D-Slides of the output
values modulated by the genes.
The BIB-scheme amends the properties of CPPNs by
modeling connections between neurons as side-effect
of their location, orientation, anatomical structure and
coincidental intersections with other neurons. This
means that, like in biological systems, genes control
global properties of the anatomy, single connections
between neurons are derived from that as side-effect.
The BIB-approach might be therefore a valuable
tool to combine gene interactions, single neuron prop-
erties and large-scale cortical and subcortical struc-
tures in one model. Rudimentary examples for this
are given in figure 3 and 7. Figure 7a shows a CPPN
for generating cortical layers. Using one coordinate
axis, eight genes contribute to the formation of neu-
ronal elements and the length and angle of the axon
and dendrite cones. The density distribution of the
output genes controlling the properties of the neurons
are depicted in fig. 7b. Like MRI- or diffusion tensor
imaging (DTI) data, the pictures show the anatomical
properties of the network in one slice (for instance,
neuron locations, projections) in a color encoding.
These data can be sampled in any resolution to gen-
erate the three-dimensional representation of the cor-
tical layers (fig. 8). In future work, such models can
serve as a model to better understand the relation be-
tween certain genes and their phenotypic influence on
the neural network.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
200

Figure 8: The neural network generated from the CPPN de-
picted in fig. 7. Neurons with axon and dendrite cones are
placed in space according to the local properties generated
by the CPPN a). These cones are used to detect connections
between neurons, depicted in b).
6 DISCUSSION
In this paper, we proposed a model for generating
complex neural networks based on an indirect encod-
ing scheme for three-dimensional patterns, which we
call Brain in a Box, or BIB. Connections between
neurons are only affected indirectly, as their position,
orientation, axon and dendrite parameters determine
the connection to other neurons. In this regard, sin-
gle genes in a BIB modify abstract properties of the
network, such as the thickness of neuronal layers, the
degree of branching or the proximity of neural groups.
Thus, BIBs reflect a way of modeling networks that,
to our mind, corresponds more to biological mech-
anisms for the emergence of complex nervous sys-
tems originating from gene regulatory networks. In
this context, BIBs might also be a valuable tool to de-
scribe structural properties of real biological networks
through gene interactions. By exploiting properties of
CPPNs, BIBs show an inherent stability across gener-
ations and but also the ability to change global prop-
erties of the network architecture to increase fitness.
Future research will focus on defining appropri-
ate fitness-functions to model certain functional prop-
erties of areas in complex nervous systems through
BIBs. These functions may include short- and long-
term plasticity for the storage of information, learning
of patterns / sequences for motor control or the detec-
tion of errors between perceived and expected infor-
mation.
REFERENCES
Basso, M. a., Uhlrich, D., and Bickford, M. E. (2005). Cor-
tical Function: A View from the Thalamus. Neuron,
45(4):485–488.
Curtis, D., Apfeld, J., and Lehmann, R. (1995). nanos
is an evolutionarily conserved organizer of anterior-
posterior polarity. Development (Cambridge, Eng-
land), 121(6):1899–910.
Goodman, D. and Brette, R. (2008). Brian: a simulator
for spiking neural networks in python. Frontiers in
neuroinformatics, 2:5.
Meinhardt, H. (2008). Models of biological pattern forma-
tion: from elementary steps to the organization of em-
bryonic axes. Current topics in developmental biol-
ogy, 81:1–63.
Raff, R. A. (1996). The Shape of Life: Genes, Develop-
ment, and the Evolution of Animal Form. University
Of Chicago Press.
Stanley, K. (2002). Evolving neural networks through aug-
menting topologies. Evolutionary computation.
Stanley, K. (2007). Compositional pattern producing net-
works: A novel abstraction of development. Genetic
Programming and Evolvable Machines, 8(2):131–
162.
Wolpert (2001). Principles of Development. Oxford Higher
Education.
TheBraininaBox-AnEncodingSchemeforNaturalNeuralNetworks
201
