
Contradiction Resolution for Foreign Exchange Rates Estimation
Ryotaro Kamimura
IT Education Center, 1117 Kitakaname, Hiratsuka, Kanagawa 259-1292, Japan
Keywords:
Self-evaluation, Outer-evaluation, Contradiction Resolution, Information-theoretic Learning, Free Energy,
SOM.
Abstract:
In this paper, we propose a new type of information-theoretic method called ”contradiction resolution.” In this
method, we suppose that a neuron should be evaluated for itself (self-evaluation) and by all the other neurons
(outer-evaluation). If some difference or contradiction between two types of evaluation can be found, the
contradiction should be decreased as much as possible. We applied the method to the self-organizing maps
with an output layer, which is a kind of combination of the self-organizing maps with the RBF networks. When
the method was applied to the dollar-yen exchange rates, prediction and visualization performance could be
improved simultaneously.
1 INTRODUCTION
In this paper, we propose a new information-theoretic
method called ”contradiction resolution,” aiming to
improve prediction and visualization performance. In
the method, a neuron is evaluated differently. If con-
tradiction between different types of evaluation can
be observed, this contradiction is decreased as much
as possible. We here consider only two types of eval-
uation, namely, self and outer-evaluation. In the self-
evaluation, a neuron’s output is evaluated for itself,
meaning that the output is determined by consider-
ing the neuron itself. On the other hand, in the outer-
evaluation, a neuron’s output is evaluated by consid-
ering all possible neighboring neurons. Then, if the
outputs from the self and outer-evaluation are differ-
ent from each other, this difference or contradiction
should be minimized.
In neural networks, no attempts have been made to
consider different types of evaluation. Some methods
have been exclusively concerned with self-evaluation.
More concretely, neurons have been forced to be as
independent as possible (Comon, 1994). On the other
hand, neurons have been forced to cooperate with
each other as much as possible in the self-organizing
maps (Kohonen, 1995), (Kohonen, 1990), (Kohonen,
1982). In the self-organizing maps, much attention
has been paid to the outer-evaluation for coopera-
tion. In our method, we can separate self and outer-
evaluation, meaning that we can examine the influ-
ence of the other neurons on a neuron. Then, we can
control this influence depending upon given objec-
tives. In this paper, we aim to improve prediction as
well as visualization performance. This improvement
is expected to be realized only when we can flexibly
control self and outer-evaluation.
2 THEORY AND
COMPUTATIONAL METHODS
2.1 Self and Outer Evaluation
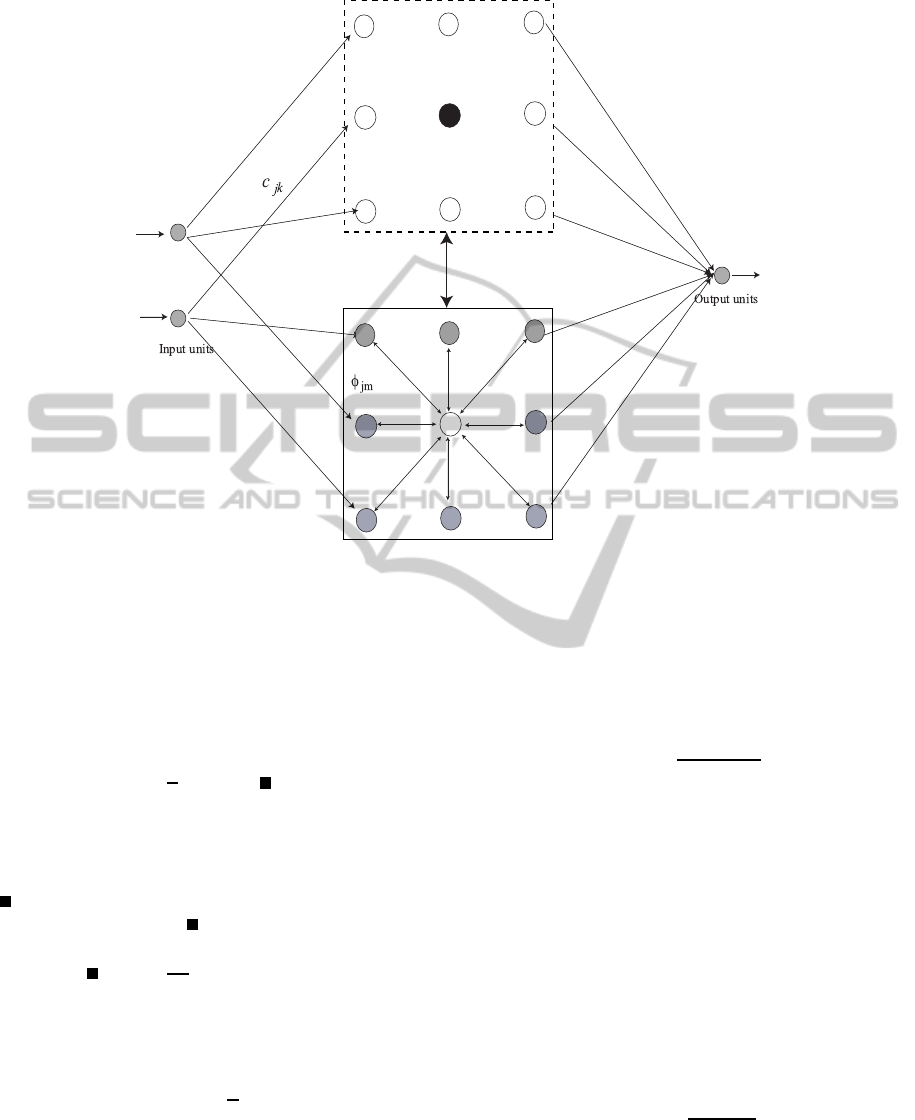
We distinguish between self- and outer-evaluation
for neurons. Figure 1(a) shows an example of self-
evaluation, where a neuron in the center produces its
output, independently of its neighbors. This is called
”self-evaluation,” because the output can be obtained
only by evaluating its own activity. In other words,
neurons respond to input patterns individually. A self-
evaluated neuron responds to input patterns without
considering the outputs of the neighboring neurons.
On the other hand, a neuron’s output is determined by
considering all neighboring neurons except the neu-
ron itself, as shown in Figure 1(b). Thus, the neu-
ron’s output is determined by evaluating all neighbor-
ing neurons’ outputs except the output from the neu-
ron itself. This situation is called ”outer-evaluation.”
529
Kamimura R..
Contradiction Resolution for Foreign Exchange Rates Estimation.
DOI: 10.5220/0004152905290535
In Proceedings of the 4th International Joint Conference on Computational Intelligence (NCTA-2012), pages 529-535
ISBN: 978-989-8565-33-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
Competitive unit
p(j|s)
x
s
k
q(j|s)
(a) Self-evaluation
Competitive units
(b) Outer-evaluation
Figure 1: Two types of evaluation, namely, self (a) and outer (b) evaluation.
2.2 Self and Outer-evaluated Outputs
Let us explain how to compute outputs by self and
outer-evaluation shown in Figure 1. The jth competi-
tive unit output can be computed by
v
s
j
= exp
−
1
2
(x
s
− c
j
)
T
(x
s
− c
j
)
, (1)
where x
s
and c
j
are supposed to represent L-
dimensional input and weight column vectors, where
L denotes the number of input units. The L×L matrix
is called a ”scaling matrix,” and the klth element of
the matrix denoted by ( )
kl
is defined by
(
)
kl
= δ
kl
1
σ
2
β
, k, l = 1, 2, · ·· , L. (2)
where σ
β
is a spread parameter. In our experiments,
the spread parameter is computed by
σ
β
=
1
β
, (3)
where β is larger than zero. The output is increased
when connection weights become closer to input pat-
terns. Now, suppose that the jth neuron is related to
the mth neuron by φ
jm
. In order to demonstrate how
our method of contradiction resolution can be used,
we applied them to self-organizing maps. For this ap-
plication, all we have to do is to replace the relation
function φ
jm
by the SOM’s neighborhood function.
The neighborhood function is defined by
φ
jc
∝ exp
kr
j
− r
c
k
2
2σ
2
γ
!
, (4)
where r
j
and r
c
denote the position of the jth and
the cth unit on the output space, and σ
γ
is a spread
parameter.
Then, the output from the jth neuron by the self-
evaluation is defined by
y
s
j
=
M
∑
m=1
δ
jm
φ
jm
v
s
m
, (5)
where M is the number of competitive units and δ
jm
is one only if j = m, and zero for all the other cases.
Thus, the output y
s
j
is equivalent to the output v
s
j
. The
normalized output can be defined
p( j | s) =
v
s
j
∑
M
m=1
v
s
m
. (6)
Then, we consider outer-evaluation, which is defined
by
z
s
j
=
M
∑
m=1
(1− δ
jm
)φ
jm
v
s
m
. (7)
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
530

The output by the outer-evaluation is the sum of all
neighboring neurons’ outputs except the jth neuron.
The normalized output is defined by
q( j | s) =
y
s
j
∑
M
m=1
y
s
m
. (8)
2.3 Contradiction Resolution
Our objective is to minimize contradiction between
the self- and outer-evaluation. To represent the con-
tradiction, we introduce the Kullback-Leibler diver-
gence between two types of neurons
KL =
S
∑
s=1
p(s)
M
∑
j=1
p( j | s)log
p( j | s)
q( j | s)
, (9)
where S is the number of input patterns. When the
KL divergence is minimized, supposing that errors
between patterns and weights are fixed, we have
p
∗
( j | s) =
q( j | s)v
s
j
∑
M
m=1
q(m | s)v
s
m
. (10)
By puting this optimal firing probability into the KL
divergence, we have the free energy function:
F = −2σ
2
S
∑
s=1
p(s)
×log
M
∑
j=1
exp
−
1
2
(x
s
− c
j
)
T
(x
s
− c
j
)
.
(11)
This equation can be expanded as
F =
S
∑
s=1
p(s)
M
∑
j=1
p( j | s)kx
s
− w
j
k
2
+2σ
2
β
S
∑
s=1
p(s)
M
∑
j=1
p( j | s)log
p( j | s)
q( j | s)
.
(12)
Thus, the free energy can be used to decrease KL di-
vergence as well as quantization errors. By differenti-
ating the free energy, we can realize the re-estimation
formula
w
j
=
∑
S
s=1
p
∗
( j | s)x
s
∑
S
s=1
p
∗
( j | s)
. (13)
3 RESULTS AND DISCUSSION
In computing the experimental results, attention was
paid to the easy reproduction and evaluation of the
final results. For easy reproduction, we used the
well-known SOM toolbox of Vesanto et al. (Vesanto
et al., 2000) because the final results of the SOM have
been very different, given the small changes in im-
plementation such as initial conditions. We have con-
firmed the reproduction of stable final results by using
this package. In addition, we used the RBF network
learning to obtain connection weight from competi-
tive units to output units without any regularization
terms, because we did not obtain favorable results by
using the regularization. For comparison, we used the
results by the conventional RBF networks in which
regularization parameters were controlled to produce
the best possible results.
3.1 Dollar-Yen Exchange Rates
We used the dollar-yen exchange rate fluctuation of
2011 for the purpose of visualization and prediction.
The two-thirds of the data were used for training and
the remaining data was for testing. We tried to exam-
ine how the prediction and visualization performance
could be improved. For example, in terms of visual
performance, we tried to extract features we could
intuitively infer from the exchange rates. Figure 2
shows the exchange rates during 2011. The period
was divided into three main periods, with an addi-
tional one showing the highest and lowest peaks. In
the first period, relatively high rates are observed. Be-
tween the first and the second period, the rates fluc-
tuated greatly, reaching the highest and lowest points.
In the second period, the rates gradually decreased.
Finally, in the third period, the rates became lowerand
more stable. We must examine how our intuition for
the exchange rates can be realized by the conventional
self-organizing maps and contradiction resolution.
3.1.1 Prediction Performance
First, we examined how our method could improve
prediction performance for the testing and training
data. Table 1 shows the summary of errors and in-
formation when the map size is 10 by 5. The mean
squared errors between outputs and targets for the
testing data were 0.240 when the parameter β was
one. Then the errors decreased gradually and reached
their lowest point of 0.054 when the parameter β was
ten. On the other hand, by the conventional SOM and
the RBF with the Ridge regression, the errors were
0.056 and 0.062, respectively. Thus, the contradiction
resolution showed the lowest errors for the MSE. Cor-
relation coefficient between targets and outputs in-
creased gradually from 0.736 (β = 1) to the lowest
of 0.933 (β = 10). On other hand, the SOM and RBF
produced 0.929 and 0.919, respectively. The correla-
ContradictionResolutionforForeignExchangeRatesEstimation
531
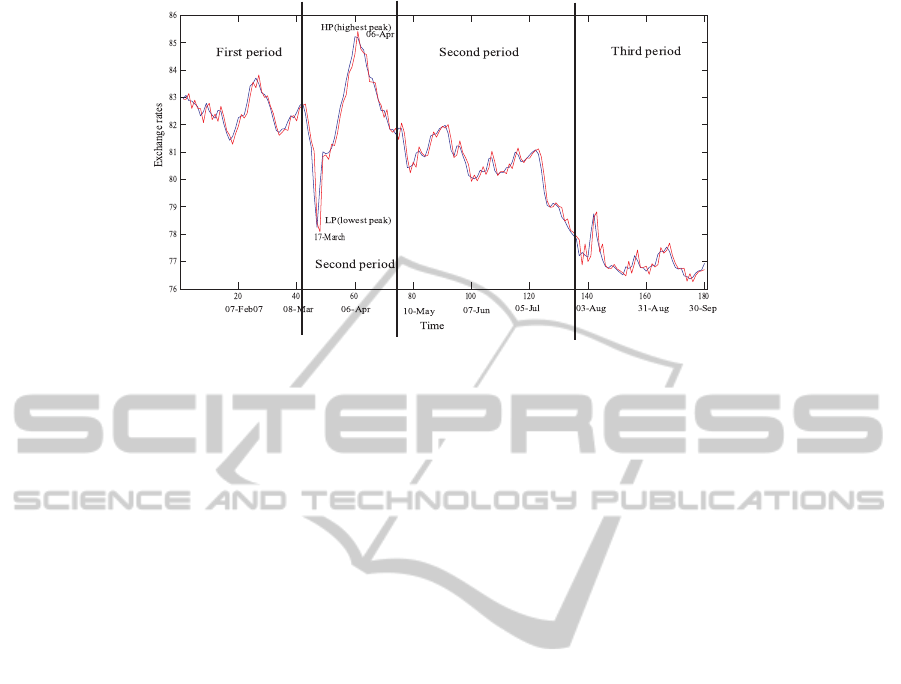
Figure 2: Training data of dollar-yen exchange rates during 2011.
tion coefficient by the contradiction was higher than
that by the conventional two methods.
Then, we computed quantization and topographic
errors for the training data. The quantization errors
decreased gradually and reached the final point of
0.437 when the spread parameter β was increased
from one to 20. By the conventional SOM, the quan-
tizatoin error was 0.505. The topographic error in-
creased from zero ((β = 1) to the maximum value
of 0.206 (β = 10). Then, the topographic error de-
creased gradually and reached the lowest point of
0.039. The topographic error by the SOM was 0.211.
Finally, mutual information between input patterns
and competitive units increased gradually when the
parameter β was increased. We could see that the
correlation coefficient between information and MSE
was -0.947. When information increased, the MSE
between outputs and targets for the testing data de-
creased. The correlation coefficient between infor-
mation and the coefficient coefficient between outputs
and targets was 0.874. When mutual information be-
tween input patterns and competitive units increased,
the correlation coefficient between outputs and targets
increased. We could also see that the correlation co-
efficient between information and quantization errors
was -0.992, meaning that quantization errors decease
when mutual information or organization increased.
This means that mutual information increase or in-
crease in organization in networks is closely related
to prediction and visualization performance except to-
pographic errors.
3.1.2 Visual Performance
Figure 3 shows the U-matrices by SOM and our
method. Figure 3 (a) shows the U-matrix by the con-
ventional SOM where we could not see clear class
boundaries. On the other hand, when the parame-
ter β was three in Figure 3(b), one straight bound-
ary in brown could be detected in the middle of
the U-matrix. When the parameter was increased to
five in Figure 3(c), the straight boundary deteriorated
slightly on the right hand side of the line. When the
parameter was further increase from 10 in Figure 3(d)
to 20 in Figure 3(f), class boundaries in warmer colors
became more complicated. Figures 4(a) and (b) show
the U-matrices and the corresponding labels by the
conventional SOM (b) and by the contradiction reso-
lution (a) when the network size was 10 by 5 and the
parameter β was ten. We can infer from these figures
that the entire period was divided into three periods,
namely, first, second and third period. In addition, the
highest and lowest peaks were separately treated as
shown in Figure 2(a). On the other hand, by the con-
ventional SOM in Figure 2(b), class boundaries on the
U-matrix and the labels were weaker.
3.2 Discussion
We here discuss visual and prediction performance
with some remarks on the possibility of our method.
First, our method could be applied to the self-
organizing maps to improve visualization perfor-
mance. In self-organizing maps, neurons are treated
equally, having no individual characteristics. The
main objective is to make neurons as similar as possi-
ble to each other. The self-organizing maps’ property
of cooperation has the effect to weaken class bound-
aries. Thus, many methods on the visualization of
SOM knowledge have been accumulated (Sammon,
1969), (Ultsch and Siemon, 1990), (Ultsch, 2003),
(Vesanto, 1999), (Kaski et al., 1998), (Yin, 2002), (Su
and Chang, 2001), (Xu et al., 2010), to cite a few. Our
contradiction resolution, as shown in the experimen-
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
532

Table 1: MSE between outputs and targets, correlation coefficient (CC) between outputs and targets, quantization errors (QE),
topographic errors (TE) and mutual information by our method and SOM for 10 by 5 map. The symbol CC
∗
represents
correlation coefficients between information (INF) and the other measures. The symbol RR represents the RBF networks
with Ridge regression.
β MSE CC QE TE INF
1 0.240 0.736 3.960 0.000 0.000
3 0.068 0.914 0.999 0.100 0.117
5 0.072 0.908 0.670 0.200 0.129
10 0.054 0.933 0.581 0.206 0.130
15 0.055 0.932 0.504 0.072 0.132
20 0.055 0.932 0.437 0.039 0.135
SOM 0.056 0.929 0.505 0.211 0.134
CC
∗
-0.947 0.874 -0.992 0.255
RR 0.062 0.919
Figure 3: U-matrices by the conventional SOM (a) and our method with 10 by 5 map whose parameter β ranged between 3
an 20 for the dollar-yen exchange rate.
tal results, can control cooperation so as to minimize
contradiction between individual and collective char-
acteristics of neurons. Experimental results showed
that this control of cooperation was effective in pro-
ducing produce clearer class boundaries.
Second, our method could improve prediction per-
formance. Compared with the results by the RBF with
the Ridge regression, our method showed better per-
ContradictionResolutionforForeignExchangeRatesEstimation
533

Figure 4: U-matrix and labels for 10 by 5 map by contradiction resolution (a) and SOM (b) for the dollar-yen exchange rate.
formance in terms of MSE and correlation coefficient
between outputs and targets for the testing data as in
Table 1. When visual performance, for example, in
terms of the U-matrix, was improved, prediction per-
formance seemed to be improved as in Table 1. In
neural learning, one of the most serious problems is
that we cannot interpret and explain why and how
neural networks can produce outputs. Internal repre-
sentations obtained by learning is so complex that it is
impossible to interpret them. In addition, we can say
that interpretation is not necessarily related to the im-
proved prediction performance. We must improve the
prediction performance, scarifying interpretation per-
formance. The present results suggest that prediction
and interpretation performance are closely related and
both types of performance can be improved simulta-
neously.
Finally, contradiction resolution can be extended
to a variety of relations between neurons. Because we
used self-organizing maps, relations between neurons
were estimated by distance between neurons on the
map. However, we can imagine a variety of relations
between neurons. One possibility is that even if two
neurons are far from each other in terms of distance
on the map, they can be considered to be close to each
other if they respond quite similarly to input patterns.
By incorporating different types of relations between
neurons, we can create different types of neural net-
work for different objectives.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
534

4 CONCLUSIONS
In this paper, we have proposed a new type of
information-theoretic method called ”contradiction
resolution.” In this method, a neuron is evaluated for
itself (self-evaluation) and by all the other neurons
(outer-evaluation). If some difference or contradic-
tion between two types of evaluation can be found, it
should be decreased as much as possible. We applied
the method to the dollar-yen exchange rate fluctua-
tion. Our method showed better performance in terms
of visualization and prediction performance. For ex-
ample, the prediction performance for the testing data
was better than that by the conventional SOM and the
RBF with ridge regression. The U-matrices obtained
by our method showed much clearer class boundaries
by which we could classify the dollar-yen exchange
rates into three periods. In addition, quantization and
topographic errors could be decreased to a level lower
than that by the conventional SOM. This means that
the prediction performance could be improved, keep-
ing fidelity to input patterns. Thus, our method shows
a possibility that prediction performance and visual-
ization performance can be improved simultaneously.
REFERENCES
Comon, P. (1994). Independent component analysis: a new
concept. Signal Processing, 36:287–314.
Kaski, S., Nikkila, J., and Kohonen, T. (1998). Methods
for interpreting a self-organized map in data analysis.
In Proceedings of European Symposium on Artificial
Neural Networks, Bruges, Belgium.
Kohonen, T. (1982). Self-organized formation of topo-
logical correct feature maps. Biological Cybernetics,
43:59–69.
Kohonen, T. (1990). The self-organization map. Proceed-
ings of the IEEE, 78(9):1464–1480.
Kohonen, T. (1995). Self-Organizing Maps. Springer-
Verlag.
Sammon, J. W. (1969). A nonlinear mapping for data struc-
ture analysis. IEEE Transactions on Computers, C-
18(5):401–409.
Su, M.-C. and Chang, H.-T. (2001). A new model of self-
organizing neural networks and its application in data
projection. IEEE Transactions on Neural Networks,
123(1):153–158.
Ultsch, A. (2003). U*-matrix: a tool to visualize clusters in
high dimensional data. Technical Report 36, Depart-
ment of Computer Science, University of Marburg.
Ultsch, A. and Siemon, H. P. (1990). Kohonen self-
organization feature maps for exploratory data anal-
ysis. In Proceedings of International Neural Network
Conference, pages 305–308, Dordrecht. Kulwer Aca-
demic Publisher.
Vesanto, J. (1999). SOM-based data visualization methods.
Intelligent Data Analysis, 3:111–126.
Vesanto, J., Himberg, J., Alhoniemi, E., and Parhankan-
gas, J. (2000). SOM toolbox for Matlab. Technical
report, Laboratory of Computer and Information Sci-
ence, Helsinki University of Technology.
Xu, L., Xu, Y., and Chow, T. W. (2010). PolSOM-a new
method for multidimentional data visualization. Pat-
tern Recognition, 43:1668–1675.
Yin, H. (2002). ViSOM-a novel method for multivari-
ate data projection and structure visualization. IEEE
Transactions on Neural Networks, 13(1):237–243.
ContradictionResolutionforForeignExchangeRatesEstimation
535
