Towards an Approach to Select Features from Low Quality Datasets
Jos´e Manuel Cadenas, Mar´ıa del Carmen Garrido and Raquel Mart´ınez
Dpt. Engineering Information and Communications, Computer Faculty, University of Murcia
30100 Campus of Espinardo, Murcia, Spain
Keywords:
Feature Selection, Low Quality Data, Fuzzy Random Forest, Fuzzy Decision Tree.
Abstract:
Feature selection is an active research in machine learning. The main idea of feature selection is to choose
a subset of available features, by eliminating features with little or no predictive information, and features
strongly correlated. There are many approaches for feature selection, but most of them can only work with
crisp data. Until our knowledge there are not many approaches which can directly work with both crisp
and low quality (imprecise and uncertain) data. That is why, we propose a new method of feature selection
which can handle both crisp and low quality data. The proposed approach integrates filter and wrapper
methods into a sequential search procedure with improved classification accuracy of the features selected.
This approach consists of steps following: (1) Scaling and discretization process of the feature set; and feature
pre-selection using the discretization process (filter); (2) Ranking process of the feature pre-selection using a
Fuzzy Random Forest ensemble; (3) Wrapper feature selection using a Fuzzy Decision Tree technique based
on cross-validation. The efficiency and effectiveness of the approach is proved through several experiments
with low quality datasets. Approach shows an excellent performance, not only classification accuracy, but also
with respect to the number of features selected.
1 INTRODUCTION
Feature selection plays an important role in the world
of machine learning and more specifically in the
classification task. On the one hand the computational
cost is reduced and on the other hand, the model
is constructed from the simplified data and this
improves the general abilities of classifiers. The
first motivation is clear, since the computation time
to build models is lower with a smaller number of
features. The second reason indicates that when
the dimension is small, the risk of “overfitting” is
reduced. As a general rule for a classification problem
with D dimensions and C classes, a minimum of
10×D×C training examples are required (Jain et al.,
2000). When it is practically impossible to obtain
the required number of training samples, reducing
features helps to reduce the size of the training
samples required and consequently to improve the
yield overall shape of the classification algorithm.
Furthermore, if the model is used from a viewpoint
practical, it requires less input data and therefore
a smaller number of measurements is necessary to
obtain of new examples. Removing insignificant
features of datasets can make the model more
transparent and more comprehensible providing a
better explanation of the system model (Luukka,
2011).
Therefore, the selection of features addresses the
problem of reducing dimensionality of the datasets by
identifying a subset of available features, which are
the most essential for classification.
There are a variety of methods in the literature
to perform feature selection (Ferreira and Figueiredo,
2012; Kabir et al., 2012; Mladenic, 2006; Vieira et al.,
2012). The feature selection should be carried out
so that the reduced dataset hold as much information
as possible to the original set. In other words the
redundant features that do not add information should
be eliminated.
There is not a feature selection method
appropriate for all types of problems. Thus, most
of feature selection methods assume that the data
are expressed with values without imprecision and
uncertainty. However, imprecision and uncertainty in
the data, leading to low quality data, may appear in
a variety of problems and these kinds of data should
be taken into account in the feature selection process,
because decisions of this process could be influenced
by the presence of imprecision and uncertainty.
Fuzzy logic has been proved as a suitable technique
to handle low quality data. Whenever imprecise and
357
Manuel Cadenas J., del Carmen Garrido M. and Martínez R..
Towards an Approach to Select Features from Low Quality Datasets.
DOI: 10.5220/0004153503570366
In Proceedings of the 4th International Joint Conference on Computational Intelligence (FCTA-2012), pages 357-366
ISBN: 978-989-8565-33-4
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

uncertain data are present, fuzzy logic is going to be
used in order to select the main features so the losses
in information from real processes could be reduced
(Su´arez et al., 2010).
Researchers are making a significant effort to
incorporate the processing of data with imprecision
and uncertainty in differentareas of machine learning:
methods of classification/regression (Bonissone et al.,
2010; S´anchez et al., 2005; Garrido et al., 2010);
discretization methods (Cadenas et al., 2012b;
S´anchez et al., 2008); etc. In this line of work, in
this paper we propose a feature selection method that,
working within the framework of the theory of fuzzy
logic, is able to deal with low quality data.
This paper is organized as follows. In Section
2 we briefly describe some of the different methods
reported in literature that perform the feature selection
process, distinguishing between methods that only
work with crisp data and methods that can work with
crisp data and low quality data. In Section 3 we
briefly describe the Fuzzy Random Forest and Fuzzy
Decision Tree techniques. We use these techniques
to define the proposed approach. In Section 4
a feature selection method is proposed. Next, in
Section 5, we present some preliminary experimental
results of proposed method. Finally, in Section 6 the
conclusions are presented.
2 FEATURE SELECTION
In many machine learning applications,
high-dimensional feature vectors impose a high
computational cost as well as the risk of “overfitting”.
Feature selection addresses the dimensionality
reduction problem by determining a subset of
available features which is the most essential for
classification.
A feature selection algorithm determines how
relevant a given feature subset “s” is for the task
“y” (usually classification or approximation of the
data). In theory, more features should provide more
discriminating power, but in practice, with a limited
amount of training data, excessive features will not
only significantly slow down the learning process, but
also cause the classifier to overfit the training data,
as irrelevant or redundant features may confuse the
learning algorithm, (Duda et al., 2001).
In the presence of hundreds or thousands of
features, researchers notice that it is common that a
large number of features are not informative because
they are either irrelevant or redundant with respect
to the class concept, (Vieira et al., 2012). In other
words, learning can be achieved more efficiently
and effectively with just relevant and non-redundant
features. However, the number of possible feature
subsets grows exponentially with the increase of
dimensionality. Finding an optimal subset is usually
intractable and many problems related to feature
selection have been shown to be NP-hard.
Researchers have studied various aspects of
feature selection. One of the key aspects is to measure
the goodness of a feature subset in determining
an optimal one. Depending on evaluation criteria,
feature selection methods can be divided into the
following categories, (Vieira et al., 2012):
• Filter Methods: this method uses measurements
as evaluation criteria to evaluate the quality of
feature subsets. Filters select subsets of features
as a pre-processing step, independently of the
chosen predictor.
• Wrapper Methods: in this case, the
classification accuracy is used to evaluate
feature subsets. Wrapper methods use the
learning machine of interest as a black-box
to score subsets of features according to their
predictive power.
• Embedded Methods: feature selection is
performed in the process of training and are
usually specific to the given modeling technique.
Proceed more efficiently by directly optimizing a
two-part objective function with a goodness-of-fit
term and a penalty for a large number of features.
• Hybrid Methods: these methods are a
combination of filter and wrapper methods.
Hybrid methods use the ranking information
obtained using filter methods to guide the search
in the optimization algorithms used by wrapper
methods. Hybrid methods are a more recent
approach and a promising direction in the feature
selection field.
However, feature selection methods can be also
categorized depending on search strategies used.
Thus, the following search strategies are more
commonly used, (Mladenic, 2006):
• Forward Selection: start with an empty set and
greedily add features one at a time.
• Backward Elimination: start with a feature
set containing all features and greedily remove
features one at a time.
• ForwardStepwise Selection: start with an empty
set and greedily add or remove features one at a
time.
• Backward Stepwise Elimination: start with a
feature set containing all features and greedily add
or remove features one at a time.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
358

• Random Mutation: start with a feature set
containing randomly selected features, add or
remove randomly selected feature one at a time
and stop after a given number of iterations.
Given the aim of this work, below we will conduct
a brief survey of feature selection methods in the
literature, according to the handling of low quality
data allowed by the method. Thus, we distinguish
between feature selection methods from crisp data
(lacking imprecise and uncertain values) and feature
selection methods from low quality data where the
uncertainty and imprecision in the dataset are explicit.
As we will be able to see the number of methods
belonging to the second category is small.
2.1 Feature Selection from Crisp Data
In the literature we can find a variety of methods to
carry out feature selection from crisp data. In this
section we briefly describe some of them without
being exhaustive.
A search strategy, which is used in various
studies, is the ant colony optimization. A
hybrid ant colony optimization based method is
proposed in (Kabir et al., 2012). This method
utilizes a hybrid search technique that combines
the wrapper and filter approaches. The algorithm
modifies the standard pheromone update and heuristic
information measurement rules based on the above
two approaches. Another algorithm is proposed
in (Vieira et al., 2012). The algorithm uses two
cooperative ant colonies that cope with two different
objectives: minimizing the number of features and
minimizing the classification error. Individual ant
colonies are used to cope with the contradictory
criteria, and are used to exchange information in the
optimization process.
Moreover in the literature we can find different
feature selection methods which are applied in
specific fields. In (Saeys et al., 2007) a feature
selection process is applied in the field of the
prediction of subsequences that code proteins (coding
potential prediction). Proteins are presented as crisp
data. For the problem of the analysis of protein
coding, Markov model is one of the most used.
Although for more accuracy and better results this
model is usually combined with other measures, such
as in (Saeys et al., 2007), where a hybrid algorithm is
proposed. This algorithm is composed in its first part
by the Markov model, which calculates a score for all
feature sets, genes in this case, and these scores serve
as input to a support vector machine that selects the
most relevant genes for protein analysis.
In (Diaz-Uriarte and de Andr´es, 2006), a Random
Forest ensemble is used to carry out the feature
selection process for classification of microarrays.
The method gets a measure of importance for each
feature based on how the permutation of the values of
that feature in the dataset affects to the classification
of the OOB dataset of each decision tree of ensemble.
There are feature selection methods which are
only developed to be applied in specific algorithms of
classification or regression. In (Guyon et al., 2002)
a method is proposed to treat with support vector
machines. In this method features are recursively
removed according to a feature ranking criteria.
Other papers make use of sequential forward
search (SFS) for feature selection. This approach is
used in (Battiti, 1994) where the mutual information
between a feature and class and between each pair of
features is used as a measure of evaluation. Another
method based on SFS is presented in (Pedrycz and
Vukovich, 2002). In this study, each feature is
indexed according to its importance using a clustering
algorithm. The importance is assessed as the
difference between the Euclidean distance of the
examples and the cluster, taking into account and
regardless a feature. The larger the difference is the
more important this feature is.
Another well known method to select features is
proposed in (Kira and Rendell, 1992). This method,
called Relief, is a filtering method that uses a neural
network and the information gain in order to select
a set of features. In (Casillas et al., 2001) a neural
network is also used to evaluate a subset of features
previously selected with a genetic algorithm.
There are methods that carry out feature selection
process and simultaneously they also develop other
functionalities. In (Ferreira and Figueiredo, 2012),
a based decision rules method carries out a feature
selection process and a discretization features process
at the same time. This method tries to minimize the
decision error in neighborhood with an unsupervised
approach. In (He et al., 2011), a method to select
features and samples is developed. This method is
based on neighborhood too, but from a supervised
approach.
2.2 Feature Selection from Low Quality
Data
As we have discussed above, there are a lot of
methods to carry out feature selection process from
crisp data. Although most of them use the fuzzy
logic theory in the development of method, they
do not perform the feature selection process from
low quality data. This is because algorithms for
preprocessing datasets with imprecise and incomplete
TowardsanApproachtoSelectFeaturesfromLowQualityDatasets
359

data are seldom studied, (S´anchez et al., 2008). This
problem is compounded by the difficulty of finding
datasets with low quality data to test developed
methods. That is why, until where we have been able
to study, there are few papers in the literature that
work with low quality data. In this subsection, we
will briefly describe these works.
In the literature there are some studies that
carry out feature selection taking into account the
uncertainty in the data through fuzzy-rough sets. In
this line, in (Jensen and Shen, 2007) a fuzzy-rough
feature selection method is presented. This method
employs fuzzy-rough sets to provide a means by
which discrete or real-valued noisy data (or a mixture
of both) can be effectively reduced without the need
for user-supplied information. Additionally, this
technique can be applied to data with continuous or
nominal decision features, and as such can be applied
to regression as well as classification datasets. The
only additional information required is in the form
of fuzzy partitions for each feature which can be
automatically derived from the data.
A widely used measure to perform feature
selection process from crisp data is the mutual
information. In (S´anchez et al., 2008), this measure is
extended with the fuzzy mutual information measure
between two fuzzified continuous features to handle
imprecise data. In this paper, this measure is used
in combination with a genetic optimization to define
a feature selection method from imprecise data.
In (Su´arez et al., 2010), the Battiti’s filter feature
selection method is extended to handle imprecise data
using the fuzzy mutual information measure.
In (Yan-Qing et al., 2011) another method that
works with low quality data is proposed. In this
case, the paper presents a study of theoretical way
for feature selection in a fuzzy decision system. This
proposal is based on the generalized theory of fuzzy
evidence.
Therefore, since the number of papers in the
literature that work directly with low quality data is
scarce, in this paper we propose a new method in
order to work with low quality data. This method
allows to handle datasets with: missing values, values
expressed by fuzzy sets, values expressed by intervals
and set-valued classes. Furthermore, the proposed
method can be classified as a Filter-Wrapper method
with sequential backward elimination on the subset of
features obtained by the Filter method.
3 FUZZY DECISION TREE AND
FUZZY RANDOM FOREST
In this section, we describe a Fuzzy Random Forest
(FRF) ensemble and Fuzzy Decision Tree (FDT),
(Cadenas et al., 2012a), which we use to define the
proposed approach.
FRF ensemble was originally presented in
(Bonissone et al., 2010), and then extended in
(Cadenas et al., 2012a), to handle imprecise and
uncertain data. In this section we describe the basic
elements that compose a FRF ensemble and the types
of data that are supported by this ensemble in both
learning and classification phases.
3.1 Fuzzy Random Forest Learning
Let be E a dataset. FRF learning phase uses
Algorithm 1 to generate the FRF ensemble whose
trees are FDTs.
Algorithm 1: FRF ensemble learning.
FRFlearning(in : E, Fuzzy Partition; out : FRF)
begin
1. Take a random sample of |E| examples with
replacement from the dataset E.
2. Apply Algorithm 2 to the subset of examples
obtained in the previous step to construct a
FDT.
3. Repeat steps 1 and 2 until all FDTs are built to
constitute the FRF ensemble.
end
Algorithm 2 shows the FDT learning algorithm,
(Cadenas et al., 2012b).
Algorithm 2 has been designed so that the
FDTs can be constructed without considering all the
features to split the nodes and maximum expansion.
Algorithm 2 is an algorithm to construct FDTs where
the numerical features have been discretized by a
fuzzy partition. The domain of each numerical feature
is represented by trapezoidal fuzzy sets, F
1
, . . . , F
f
so each internal node of the FDTs, whose division
is based on a numerical feature, generates a child
node for each fuzzy set of the partition. Moreover,
Algorithm 2 uses a function, denoted by χ
t,N
(e),
that indicates the degree with which the example e
satisfies the conditions that lead to node N of FDT t.
Each example e is composed of features which can
take crisp, missing, interval, fuzzy values belonging
(or not) to the fuzzy partition of the corresponding
feature. Furthermore, we allow the class feature to be
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
360

Algorithm 2: Fuzzy decision tree learning.
FDecisionTree(in : E, Fuzzy Partition; out : FDT)
begin
1. Assign χ
Fuzzy
Tree,root
(e) = 1 to all examples
e ∈ E with single class and replicate the
examples with set-valued class initializing their
weights according to the available knowledge
about their classes.
2. Let A be the feature set (all numerical
features are partitioned according to the Fuzzy
Partition).
3. Choose a feature to the split at the node N.
3.1. Make a random selection of features from
the set A.
3.2. Compute the information gain for
each selected feature using the values
χ
Fuzzy
Tree,N
(e) of each e in node N taking
into account the function µ
simil(e)
for the
cases required.
3.3. Choose the feature such that information
gain is maximal.
4. Divide N in children nodes according to
possible outputs of the selected feature in the
previous step and remove it from the set A. Let
E
n
be the dataset of each child node.
5. Repeat steps 3, 4 with each (E
n
,A) until the
stopping criteria is satisfied.
end
set-valued. These examples (according to the value of
their features) have the following treatment:
• Each example e used in the training of the FDT
t has assigned an initial value χ
t,root
(e) = 1 to
all examples with a single class and replicate the
examples with set-valued class and initialize their
weights according to the available knowledge
about their class.
• According to the membership degree of the
example e to different fuzzy sets of partition of
a split based on a numerical feature:
– If the value of e is crisp, the example e
may belong to one or two children nodes,
i.e., µ
fuzzy
set partition
(e) > 0. In this case
χ
t,childnode
(e) = χ
t,node
(e) ·µ
fuzzy
set partition
(e).
– If the value of e is a fuzzy value matching
with one of the sets of the fuzzy partition
of the feature, e will descend to the child
node associated. In this case, χ
t,childnode
(e) =
χ
t,node
(e).
– If the value of e is a fuzzy value different
from the sets of the fuzzy partition of the
feature, or the value of e is an interval value,
we use a similarity measure, µ
simil
(·), that,
given the feature “Attr” to be used to split
a node, measures the similarity between the
values of the fuzzy partition of the feature and
fuzzy values or intervals of the example in that
feature. In this case, χ
t,childnode
(e) = χ
t,node
·
µ
simil
(e).
– When the example e has a missing value,
the example descends to each child node
node
h
, h = 1, . . . , H
i
with a modified value
proportionately to the weight of each child
node. The modified value for each node
h
is calculate as χ
node
h
(e) = χ
node
(e) ·
Tχ
node
h
Tχ
node
where Tχ
node
is the sum of the weights of the
examples with known value in the feature i
at node node and Tχ
node
h
is the sum of the
weights of the examples with known value in
the feature i that descend to the child node
node
h
.
3.2 Fuzzy Random Forest Classification
The fuzzy classifier module operates on FDTs of
the FRF ensemble using one of these two possible
strategies: Strategy 1 - Combining the information
from the different leaves reached in each FDT to
obtain the decision of each individual FDT and then
applying the same or another combination method to
generate the global decision of the FRF ensemble;
and Strategy 2 - Combining the information from all
reached leaves from all FDTs to generate the global
decision of the FRF ensemble.
4 THE PROPOSED APPROACH
The proposed approach is classified as a hybrid
method with sequential backward elimination on the
subset of features obtained by the Filter method.
Figure 1 shows the framework of the proposed
approach which consists of main steps: (1) Scaling
and discretization process of the feature set; and
feature pre-selection using the discretization process;
(2) Ranking process of the feature pre-selection
using FRF ensemble; and (3) Wrapper feature
selection using a classification technique based on
cross-validation. Moreover, in this framework(Figure
1), we want to emphasize that in each step, the
approach obtains information useful to the user
(pre-selected feature subset, ranking of the feature
subset and optimal feature subset).
Figure 2 presents the details of the proposed
method.
TowardsanApproachtoSelectFeaturesfromLowQualityDatasets
361

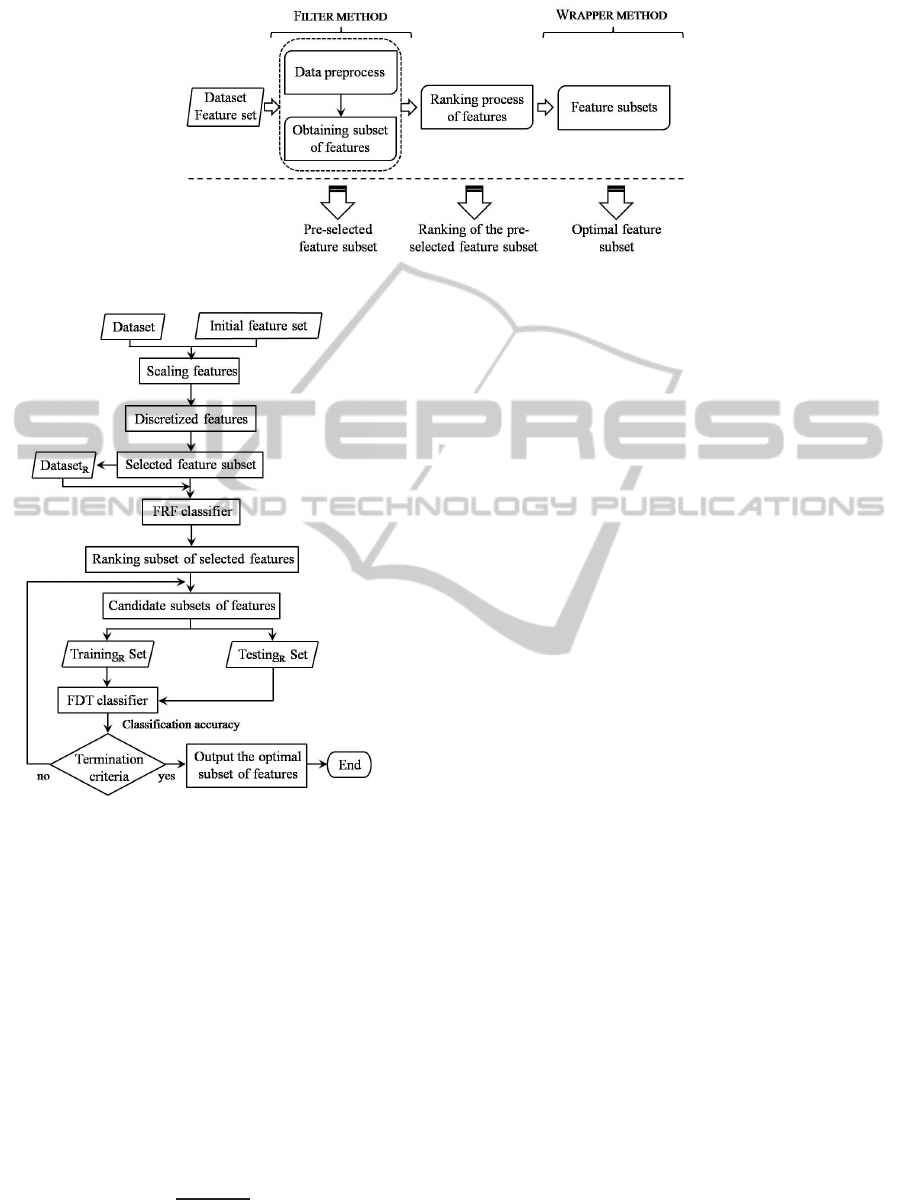
Figure 1: Framework of the proposed approach.
Figure 2: Details of the proposed approach.
The main steps and algorithms are discussed in the
following subsections.
4.1 Filter Method for Feature
Pre-selection
4.1.1 Data Preprocess
Initially, the data are treated to the proper operation
of the proposed approach. We carry out a scaling and
discretization.
The main advantage of scaling is to avoid features
in greater numeric ranges dominating those in smaller
numeric ranges. Each feature is linearly scaled to
the range [0,1] by v
′
=
v−min
a
max
a
−min
a
, where v is original
value, v
′
is scaled value, and, max
a
and min
a
are upper
and lower bounds, respectively, of the feature a.
In (Cadenas et al., 2012b), a hybrid method
for the fuzzy discretization of numerical features is
presented. The aim of this method is to find optimized
fuzzy partitions to obtain a high classification
accuracy with the classification techniques. The
method makes use of two techniques: a FDT and
a Genetic Algorithm. This method consists of two
stages: in the first one, a FDT is used to generate a set
of initial divisions in the numerical feature domain; in
the second one, a Genetic Algorithm is used to find a
fuzzy partition by refining the initial set of divisions,
determining the cardinality, and defining their fuzzy
boundaries. This discretization method is used in our
approach to feature pre-selection.
4.1.2 Obtaining Pre-selected Features
For steps (1), (2) and (3) of the framework of
the proposed approach, we use Fuzzy Random
Forest (Cadenas et al., 2012a) and FDT (Cadenas
et al., 2012a) learning techniques. One of the
characteristics of these two techniques is the need
to have datasets with numerical features discretized.
They use the optimized partition obtained in the
previous preprocess. Note that in this discretization
process some features may be discretized into a single
interval.
Hence, these latter features can be removed
without affecting the discriminating power of the
original dataset. Thus, after removing these features,
we obtain a pre-selection of the feature set. With this
subset, we transform the initial dataset into another
dataset that contains only the pre-selected features.
4.2 Ranking Process
From pre-selected feature subset and the
corresponding dataset, we propose a measure in
order to calculate the importance of these features.
This measure uses information obtained by an FRF
ensemble obtained from these data.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
362

From the feature subset and the dataset obtained
with the filter method, we apply FRF technique. With
the FRF ensemble obtained, Algorithm 3 describes
how information provided for each FDT of the
ensemble is compiled and used to measure the
importance of each feature.
Algorithm 3: Information of the FRF technique.
INFFRF (in: E, Fuzzy Partitions, T; out: INF)
Building the Fuzzy Random Forest (Algorithm 1)
For each FDT t=1 to T of the FRF ensemble
Save the feature a chosen to split each node N,
number of examples E
Na
and the depth of that
node P
Na
, in INF
a
.
Obtain the classification accuracy Acc
t
of the
FDT t with its corresponding OOB
t
dataset.
More specifically, the information we get from
each FDT t for each feature a is the following:
• Number of examples of node N (E
Na
) where the
feature a has been selected as best candidate to
split it.
• Depth level of node N (P
Na
) where feature a has
been selected as best candidate to split it.
• Classification accuracy Acc
t
of FDT t when
classify the dataset OOB
t
.
Algorithm 4 details how the information INF
obtained from the FRF ensemble is combined where
p
i
is the weight we assign to a feature a depending
on the place where it appears in the FDT t. After the
information is combined, the output of this algorithm
is a matrix (IMP) where is stored for each FDT t and
for each feature a, the importance value obtained in
the FDT t for the feature a.
The idea behind the measure of importance of
each feature is using the features of the FDTs
obtained and the decision nodes built with them.
One feature that appears at the top of a FDT is
more important in that FDT than another feature that
appears in the lower nodes. And, a FDT that has an
classification accuracy greater than another to classify
the corresponding OOB (dataset independent of the
training dataset) is a better FDT. The final decision is
agreed by the information obtained for all FDTs.
As a result of the Algorithm 4, we obtain for each
FDT of FRF ensemble a ranking of importance of
the features. Specifically, we will have T rankings of
importance for each feature a. Applying an operator
OWA, we add all into one ranking. This final ranking
indicates the definitive importance of the features.
OWA operators (Ordered Weighted Averaging)
were introduced by Yager in 1988, (Yager, 1988).
Algorithm 4: Combining information INF.
IMPFRF( in: INF, T; out: IMP)
For each FDT t=1 to T
For each feature a=1 to |A|
Repeat for all nodes N where feature a appears
If P
Na
= i then IMP
ta
= IMP
ta
+ p
i
· E
Na
, with
i ≥ 0 and P
rootnode
= 0
For each feature a=1 to |A|
IMP
ta
=
IMP
ta
−min(IMP
t
)
max(IMP
t
)−min(IMP
t
)
IMP
ta
= IMP
ta
· OOB
t
The vector IMP
t
is ordered in descending order,
IMP
t
σ
t
where σ
t
is the permutation obtained when
ordering IMP
t
OWA operators are known as compensation
operators. They are operators of aggregation of
numeric information that consider the order of the
assessments that will be added.
Definition 1. Let Y = {y
1
, . . . , y
n
} be, with y
i
∈ [0, 1],
the set of assessments that we want to add and W =
{w
1
, . . . , w
n
} its associated weight vector, such that
w
i
∈ [0, 1], with 1 ≤ i ≤ n, and
∑
n
i=1
w
i
= 1. OWA
operator, O, is defined as:
O(y
1
, . . . , y
n
) =
n
∑
j=1
w
j
· b
j
where b
j
is the j-th largest value in the set Y (B =
{b
1
, . . . , b
n
} such that b
i
≥ b
j
, if i < j).

When applying the OWA operator, we are
considering every tree of the ensemble as an expert
giving his opinion about the importance of the
problem variables. In our case, we have T ordered
sets. Given a weight vector W, the vector RANK
represents the ranking of the pre-selected features
subset and is obtained as follows:
OWAIMP
t
= W · IMP
t
σ
t
, for t = 1, . . . , T
RANK
a
=
T
∑
t=1
OWAIMP
tσ
t
(a)
, for a = 1, . . . , |A|
The vector RANK is ordered in descending order:
RANK
σ
.
4.3 Wrapper for Feature Selection
Once the ranking of the pre-selected feature subset,
RANK
σ
, is obtained, we have to find an optimal subset
of features. One option to search the optimal subset is
by deleting a single feature at a timeuntil the specified
TowardsanApproachtoSelectFeaturesfromLowQualityDatasets
363

criteria is fulfilled. The process starts from the whole
set of the pre-selected features and eliminates features
sequentially backward until the desired feature subset
is achieved. We will eliminate the features with lower
value in the ranking obtained.
All subsets of features obtained by this process
are evaluated by a machine learning method. The
dataset obtained from each subset of features is
used to learn and test. We use a machine learning
method that supports low quality data with a process
of cross-validation. The subset with the highest
classification accuracy value will be the optimal
feature subset obtained by the proposed approach.
5 EXPERIMENTAL RESULTS
5.1 The Datasets and the Experimental
Setup
The proposed approach is going to evaluate by means
of experiments on various datasets selected from
the UCI machine learning repository (Asuncion and
Newman, 2007). These datasets used to test the
proposed approach are summarized in Table 1. We
have included in these datasets a 10% of fuzzy values.
This percentage does not affect to the class feature.
In addition, some of these datasets contain missing
values.
Table 1: Datasets.
Dataset Abbr |E| |A| I F ?
Australian credit AUS 690 14 (6-8) 2 Y Y
German (credit card) GER 1000 24 (24-0) 2 Y N
Statlog Heart HEA 270 13 (13-0) 2 Y N
Ionosphere ION 351 34 (34-0) 2 Y N
Pima Indian Diabetes PIM 768 8 (8-0) 2 Y Y
Sonar SON 208 60 (60-0) 2 Y N
SPECTF heart SPEC 267 44 (44-0) 2 Y N
Wis. Br. Cancer (org) WBC 699 9 (9-0) 2 Y Y
Wis. Diag. Br. Cancer WDC 569 31 (31-0) 2 Y N
Wine WIN 178 13 (13-0) 3 Y N
Table 1 shows the number of examples (|E|),
the number of features (|A|) (in brackets, numerical
and nominal features) and the number of classes
(I) for each dataset. Column F indicates that each
dataset contains fuzzy values and column ? indicates
that contains missing values. “Abbr” indicates the
abbreviation of the dataset used in the experiments.
The experimental parameters are as following:
• Parameters of the FRF ensemble (Algorithm 1).
We have used the default values derived from the
analysis performed in (Bonissone et al., 2010):
Table 2: Results.
Unselect Pre-selection Opt. Selection p-val
% accur. #fe. % accur. #fe. % accur. #fe.
AUS 84.78
3.07
14 84.78
3.07
14 85.94
2.74
N 2 0.068
GER 73.90
3.44
24 73.90
3.44
19 74.40
3.21
N 17 0.028
HEA 82.72
1.55
13 82.72
1.55
11 84.07
2.81
N 5 0.029
ION 93.16
2.36
34 93.16
2.36
19 93.45
1.93
N 15 0.027
PIM 75.78
2.60
8 75.78
2.60
8 76.82
2.47
N 4 0.029
SON 80.77
3.46
60 80.77
3.46
17 81.28
3.37
N 16 0.500
SPEC 82.43
5.22
44 82.43
5.22
7 83.17
3.86
H 5 0.208
WBC 96.63
1.77
9 96.63
1.77
9 96.43
1.67
H 6 0.594
WDC 95.43
1.80
31 95.43
1.80
11 95.43
1.80
− 9 0.294
WIN 97.19
1.96
13 97.19
1.96
8 97.19
1.96
− 4 1.000
– Size of the ensemble: 120 FDTs
– Random selection of features from the set of
available features: log
2
|A|
• Vector to combine the information of INF
(Algorithm 4): p = (1,
6
7
,
2
3
,
2
4
,
2
5
,
2
P
Na
+1
, . . .) with
P
Na
the depth of node N which contains the
feature a. Vector values are defined inversely
proportional to the depth of the considered node,
relaxing the decrease between levels.
• Normalized weights vector for calculating
OWAIMP: W = (1,
1
2
, . . . ,
1
|A|
) with |A| the
number of features. This vector defines a
standard preference relation when using these
operators.
• In wrapper selection:
– Cross-validation is used to evaluate the
performance of the feature selection. The
number of folds is set to be k=5.
– FDT technique (Algorithm 2) using a complete
selection of features on nodes to expand, and
using as stop criteria: to find a pure node or
minimum number of examples.
5.2 Evaluation of the Classification
Performance
This experiment is designed to evaluate the
performance of the proposed approach. The
performance of the selected feature subset is
evaluated by FDT technique using an independent
testing data. Table 2 indicates the percentage of
average classification accuracy (mean and standard
deviation) for a 5-fold cross-validation test and the
selected features subset.
Table 2 shows average classification accuracy
for the initial dataset (Unselect), for the dataset
using only the pre-selection feature subset and for
the dataset with the optimal selected feature subset
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
364

Table 3: Feature subsets.
Ranking of the pre-selected features Optimal selected subset
AUS 14-8-10-13-7-9-5-3-2-6-12-1-4-11 8-14
GER 3-1-2-4-6-5-10-11-20-21-16-9-17-24-12-14-19-18-22 1-2-3-4-5-6-9-10-11-12-14-16-17-19-20-21-24
HEA 13-12-3-10-11-9-5-1-7-2-6 3-10-11-12-13
ION 5-8-24-16-7-1-18-14-10-34-25-23-30-17-6-9-32-33-4 1-5-6-7-8-10-14-16-17-18-23-24-24-25-30-34
PIM 8-2-6-7-5-3-1-4 2-6-7-8
SON 11-51-28-12-49-36-58-52-2-60-44-16-55-53-54-26 2-11-12-16-28-36-44-49-51-52-53-54-55-58-60
SPEC 40-16-44-18-38-23-27 16-18-38-40-44
WBC 2-3-6-4-1-7-9-8-5 2-3-6-4-7-1
WDC 23-8-21-24-29-28-22-20-19-10-12 8-19-20-21-22-23-24-28-29
WIN 13-7-10-12-1-5-9-8 7-10-12-13
retrieved by the proposed approach. Moreover, in
each case we show the number of features of the
dataset and the p-value for the classification accuracy
of Unselect and Optimal selection.
To obtain these p-values, we make an analysis
of results using the Wilcoxon signed-rank
non-parametric test. This test is a pairwise test
that aims to detect significant differences between
results. Under the null hypothesis, it states that
the results are equivalent, so a rejection of this
hypothesis implies the existence of differences in the
classification accuracy.
Table 3 shows the ranking of the pre-selected
feature subset and the optimal selected feature subset
retrieved by the proposed approach.
The results indicate that the optimal feature
subset selected by the proposed approach has a very
good classification performance when working with
low quality datasets. For AUS, GER, HEA, ION
and PIM datasets there are significant differences
among the observed results with a significance level
below 0.07, being the classification accuracy of the
Optimal selection better than Unselect; and for other
datasets do not exist significance differences between
the classification accuracy of Unselect and Optimal
selection, but, the proposed approach retrieves a
smaller number of features.
6 REMARKS AND
CONCLUSIONS
Feature selection is one of the main issues in
machine learning and more specifically in the
classification task. An appropriate feature selection
has demonstrated great promise for enhancing the
knowledge discovery and models interpretation.
There are a variety of methods in the literature
to perform feature selection. But, most feature
selection methods assume that data are expressed with
values without explicit imprecision and uncertainty.
However, explicit imprecision and uncertainty in
the data, leading to low quality data may appear
in a variety of problems. Researchers are
making a significant effort to incorporate the
processing of data with imprecision and uncertainty
in different areas of machine learning: methods of
classification/regression, discretization methods, etc.
We have proposed a feature selection method that
working within the framework of the theory of fuzzy
logic is able to deal with low quality data.
The proposed approach is classified as a hybrid
method that combines the filter and wrapper methods.
The framework consists of main steps: (1) Scaling
and discretization process of the feature set; and
feature pre-selection using the discretization process;
(2) Ranking process of the feature pre-selection using
a Fuzzy Random Forest ensemble; and (3) Wrapper
feature selection using a classification techniques
based on cross-validation. This wrapper method starts
from the complete set of the pre-selected features
and successively eliminates features until the desired
feature subset is achieved. We eliminate the feature
with the lowest ranking obtained. Subsets of features
obtained by this process are evaluated using the FDT
technique.
In each step, the approach obtains information
useful to the user: pre-selected feature subset, ranking
of the feature subsets and optimal feature subset.
The experiments were designed to evaluate the
performance of the proposed approach with low
quality dataset. The results indicate that the optimal
feature subset selected by the proposed approach has
a good classification performance when working with
low quality datasets. Proposed approach retrieves
a smaller number of features that achieve a better
performance than the unselect. According to our
results, we believe that it is interesting to follow this
line of work.
TowardsanApproachtoSelectFeaturesfromLowQualityDatasets
365

ACKNOWLEDGEMENTS
Supported by the project TIN2011-27696-C02-02
of the “Ministerio de Econom´ıa y Competitividad”
of Spain. Thanks also to the Funding Program
for Research Groups of Excellence with code
“04552/GERM/06” granted by the “Agencia de
Ciencia y Tecnolog´ıa” of the Region of Murcia
(Spain). Also, Raquel Mart´ınez is supported by the
scholarship program FPI from this Agency of the
Region of Murcia.
REFERENCES
Asuncion, A. and Newman, D. J. (2007).
UCI Machine Learning Repository,
http://www.ics.uci.edu/ mlearn/MLRepository.html.
Irvine, CA: University of California, School of
Information and Computer Science.
Battiti, R. (1994). Using mutal information for selection
features in supervised neural net learning. IEEE
Transactions on Neural Networks, 5:537–550.
Bonissone, P. P., Cadenas, J. M., Garrido, M. C., and
D´ıaz-Valladares, R. A. (2010). A fuzzy random forest.
International Journal of Approximate Reasoning,
51(7):729–747.
Cadenas, J. M., Garrido, M. C., Mart´ınez, R., and
Bonissone, P. P. (2012a). Extending information
processing in a fuzzy random forest ensemble. Soft
Computing, 16(5):845–861.
Cadenas, J. M., Garrido, M. C., Mart´ınez, R., and
Bonissone, P. P. (2012b). Ofp
class: a hybrid
method to generate optimized fuzzy partitions for
classification. Soft Computing, 16(4):667–682.
Casillas, J., Cord´on, O., del Jes´us, M. J., and Herrera,
F. (2001). Genetic feature selection in a fuzzy
rule-based classification system learning process for
high-dimensional problems. Information Sciences,
139:135–157.
Diaz-Uriarte, R. and de Andr´es, S. A. (2006). Gene
selection and classification of microarray data using
random forest. BMC Bioinformatics, 7(3).
Duda, R. O., Hart, P. E., and Stork, D. G. (2001). Pattern
Classification. Wiley-Interscience Publication.
Ferreira, A. J. and Figueiredo, M. A. T. (2012).
An unsupervised approach to feature
discretization and selection. Pattern Recognition
(doi:10.1016/j.patcog.2011.12.008).
Garrido, M. C., Cadenas, J. M., and Bonissone, P. P.
(2010). A classification and regression technique to
handle heterogeneous and imperfect information. Soft
Computing, 14:1165–1185.
Guyon, I., Weston, J., Barnhill, S., and Bapnik, V. (2002).
Gene selection for cancer classification using support
vector machine. Machine Learning, 46:389–422.
He, Q., Xie, Z., Hu, Q., and Wu, C. (2011).
Neighborhood based sample and feature selection
for svm classification learning. Neurocomputing,
74:1585–1594.
Jain, A. K., Duin, R. P. W., and Mao, J. (2000). Statistical
pattern recognition: a review. IEEE Trans. Pattern
Anal. Mach. Intell., 22(1):4–37.
Jensen, R. and Shen, Q. (2007). Fuzzy-rough sets assisted
attribute selection. IEEE Transactions on Fuzzy
Systems, 15(1):73–89.
Kabir, M. M., Shahjahan, M., and Murase, K. (2012).
A new hybrid ant colony optimization algorithm for
feature selection. Expert System with Applications,
39:3747–3763.
Kira, K. and Rendell, L. (1992). A practical approach
to feature selection. In Proceedings of the Ninth
International Conference on Machine Learning,
pages 249–256.
Luukka, P. (2011). Feature selection using fuzzy entropy
measures with similarity classifier. Expert Systems
with Applications, 38:4600–4607.
Mladenic, D. (2006). Feature selection for dimensionality
reduction. subspace, latent structure and feature
selection, statistical and optimization. SLSFS 2005,
Lecture Notes in Computer Science, 3940:84–102.
Pedrycz, W. and Vukovich, G. (2002). Feature analysis
through information granulation and fuzzy sets.
Pattern Recognition, 35:825–834.
Saeys, Y., Rouze, P., and de Peer, Y. V. (2007). In search of
the small ones: improved prediction of short exons in
vertebrates, plants, fungi and protists. Bioinformatics,
23(4):414–420.
S´anchez, L., Suarez, M. R., and Couso, I. (2005). A fuzzy
definition of mutual information with application
to the desing of genetic fuzzy classifiers. In
Proceedings of the International Conference on
Machine Intelligence, pages 602–609.
S´anchez, L., Su´arez, M. R., Villar, J. R., and Couso,
I. (2008). Mutual information-based feature
selection and partition design in fuzzy rule-based
classifiers from vague data. International Journal of
Approximate Reasoning, 49:607–622.
Su´arez, M. R., Villar, J. R., and Grande, J. (2010). A feature
selection method using a fuzzy mutual information
measure. International Journal of Reasoning-based
Intelligent Systems, 2:133–141.
Vieira, S. M., Sousa, J. M. C., and Kaymak, U. (2012).
Fuzzy criteria for feature selection. Fuzzy set and
System, 189:1–18.
Yager, R. R. (1988). On ordered weighted averaging
aggregation operators in multicriteria decision
making. IEEE transactions on Systems, Man and
Cybernetics, 18:183–190.
Yan-Qing, Y., Ju-Sheng, M., and Zhou-Jun, L. (2011).
Attribute reduction based on generalized fuzzy
evidence theory in fuzzy decision systems. Fuzzy Sets
and Systems, 170:64–75.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
366