Recovery of Sequential and Non Sequential Memories with a Neural

Mass Model

Filippo Cona and Mauro Ursino

Department of Electronics, Computer Sciences and Systems, University of Bologna, Via Venezia 52, Cesena, Italy

Keywords: Neural Mass Models, Memory, Neural Assemblies, Autoassociative Networks.

Abstract: A neural model for the recovery of learnt patterns is presented. The model simulates the theta-gamma

activity associated to memory recall. Two versions of the model are described: the first can learn generic

patterns without a given order, while the second learns patterns in a specific sequence. The latter has been

implemented to overcome the limited recovery capacity of the former. The network is trained using Hebbian

and anti-Hebbian paradigms, and exploits excitatory and inhibitory mutual synapses. The results show that

autoassociative memories for storage and recovery of multiple patterns can be built using biologically

inspired models which simulate brain rhythms, and that the model which learns sequences can recover much

more patterns.

1 INTRODUCTION

The execution of complex tasks requires the

integration of many different pieces of information

spread across the whole brain. A widely used

concept to describe the large-scale integration in the

brain is the Neural Assembly (NA), which is defined

as the ensemble of neurons that take part in the

realization of a single cognitive task.

A popular hypothesis, named “binding by

synchronization” (Varela et al., 2001); (Singer,

1999), suggests that the formation of NAs is

obtained through the phase synchronization of

neural groups in the gamma band (>25Hz).

According to this hypothesis, a NA can be formed

rapidly and can rapidly be disrupted under the

influence of external or internal events to make

place for alternative NAs. Furthermore, the recent

observation that gamma rhythms are modulated by

slower theta rhythms (4-7Hz) suggests the idea that

the construction and degradation of gamma rhythms

is under control of theta oscillations (Canolty et al.,

2006); (Doesburg et al., 2009).

Several mathematical models in past years

described the formation and segmentation of NAs,

simulating how the brain can assign a neural group

to the correct assembly, while maintaining it

separated from neural groups which belong to other

assemblies. However, these models used very simple

oscillating neural units, such as Wilson Cowan or

relaxations oscillators (Wang et al., 1990); (von der

Malsburg and Buhmann, 1992); (Wang and Terman,

1997); (Ursino et al., 2003); (Ursino et al., 2009),

which are unable to simulate realistic brain rhythms.

A recent work addresses the same issue using a more

sophisticate model, able to mimic the electrical

activity in cortical regions (Cona et al., 2012). Using

a mathematical model for the simulation of brain

activity, known as neural mass model (NMM), the

authors proposed a neural architecture that can learn

different NAs and evoke them separated in time.

However, they were able to evoke just three gamma

oscillations within each theta cycle, while many

works suggest that this number can be between 4

and 7 (Cowan, 2000); (Miller, 1956).

The model itself suggested how to overcome this

limitation: by visual inspection of the simulated

waveforms, one can observe that most of the time

between two consecutive gamma oscillations is

‘wasted’ to determine which NA should follow. So

we inferred that, if patterns are learnt in a specific

sequence, the model should be able to evoke much

more NAs within a single theta cycle. This

corresponds to psychophysical observations.

In the following, we will show the architecture of

the NMM used to memorize non-sequential NAs and

the changes adopted to learn a sequence of NAs. The

different performance of the two models will be

outlined.

547

Cona F. and Ursino M..

Recovery of Sequential and Non Sequential Memories with a Neural Mass Model.

DOI: 10.5220/0004154005470551

In Proceedings of the 4th International Joint Conference on Computational Intelligence (NCTA-2012), pages 547-551

ISBN: 978-989-8565-33-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 METHOD

2.1 The Cortical Column

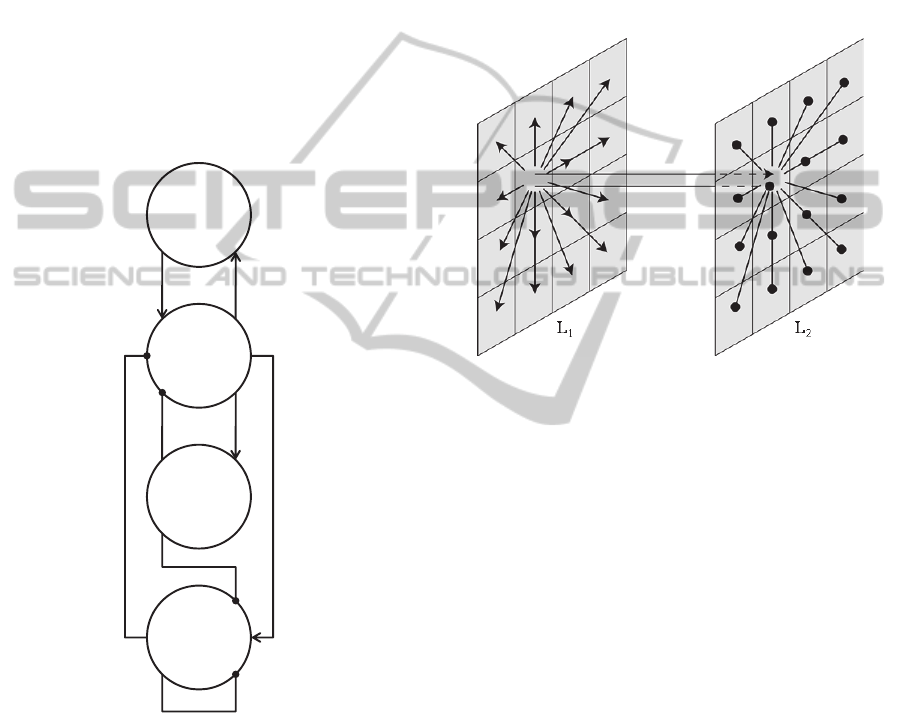
The fundamental unit of our network is the model of

a cortical column. It consists of four interconnected

neural populations (Figure 1), which are pyramidal

cells, excitatory interneurons and inhibitory

interneurons with slow and fast kinetics

(respectively referred to as GABA

A,slow

and

GABA

A,fast

). The interaction of these populations

allows the cortical column to generate different

oscillatory activities, while the output of the model

(the simulated EEG signal) is given by the

membrane potential of the pyramidal cells. See

Ursino et al., (2010) for more details on the model.

Figure 1: Connectivity between neural populations in the

model of a cortical region.

2.2 Recall of Non-sequential Patterns

The neural network consists of 2 layers (L

and L

)

of M×N cortical columns each, (Figure 2). The first

receives the external input and sends its output to the

second layer. The second generates the cortical

output. The network can learn patterns (NAs) of

features. Each feature corresponds to a position in

both layers and therefore is associated with two

oscillatory columns, one in L

and one in L

Each unit in L

and L

is represented through a

cortical column, according to the diagram in Figure

1. Moreover, units in the same layer communicate

through lateral synapses, according to the schematic

representation in Figure 3. These synapses were

learnt via Hebbian or anti-Hebbian mechanisms,

during a training (storage phase) in which seven

complete patterns (without any lacking feature) were

given separately to the network. After training, the

network was tested using incomplete patterns as

inputs (recovery phase).

Figure 2: Architecture of the two layers: arrows indicate

connections toward pyramidal cells, while circles indicate

connections toward GABA

A,fast

interneurons.

During the recovery phase L

works as an

autoassociative memory, i.e., it serves the main

function of recovering the lacking information when

the patterns are not totally stimulated. Hence, just a

few features are sufficient to evoke the whole NA

they belong to. The units in L

exhibit an oscillatory

activity in the theta band which drives L

. This

behaviour is obtained by training the excitatory

lateral connections in L

with the Hebb rule, i.e.,

reinforcing excitation among features which belong

to the same pattern and so are simultaneously active.

The excitation between features belonging to the

same NA ensures the complete recovery of lacking

information. However, excitation would lead

neurons to the upper saturation (i.e., to a maximal

excitation). The theta oscillation emerges thanks to

the presence of inhibitory populations with slow

synaptic kinetics (GABA

A,slow

interneurons) which

progressively inhibit units through synapses with a

time constant of 34 ms.

plays two roles: it makes the cortical columns

oscillate synchronously in the gamma band when

they encode for the same NA (binding), and out-of-

synch if they belong to different NAs

Excitatory

interneurons

Pyramidal

cells

Inhibitory

interneurons

(slow)

Inhibitory

interneurons

(fast)

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

548

(segmentation). The synchronicity is obtained

through lateral inhibitory synapses, trained with the

Hebb rule which link pyramidal neurons in the pre-

synaptic units to GABA

A,fast

interneurons in all units

which encode for the same NA(Figure 3). As

demonstrated in previous works (Bartos et al.,

2002); (Bartos et al., 2007); (Ursino et al., 2010),

reciprocal fast inhibition is a powerful mechanism to

ensure synchronization of gamma rhythms. As a

consequence of this mechanisms, all units in the

same pattern become part of a bigger gamma

oscillator. The segmentation is obtained by training

another set of synapses from pyramidal to

GABA

A,fast

interneurons with an anti-Hebbian rule

(i.e., a synapse is reinforced when the pre-synaptic

unit is active, but the post-synaptic unit is silent).

The latter synapses, however, have a much faster

dynamics compared with the previous ones (rising

time less than 1 ms). These can simulate ultra-fast

AMPA synapses. This mechanism induces a very

fast inhibition between columns in different patterns

of L

, so that different features in different patterns

tend to desynchronise (Cona et al., 2012).

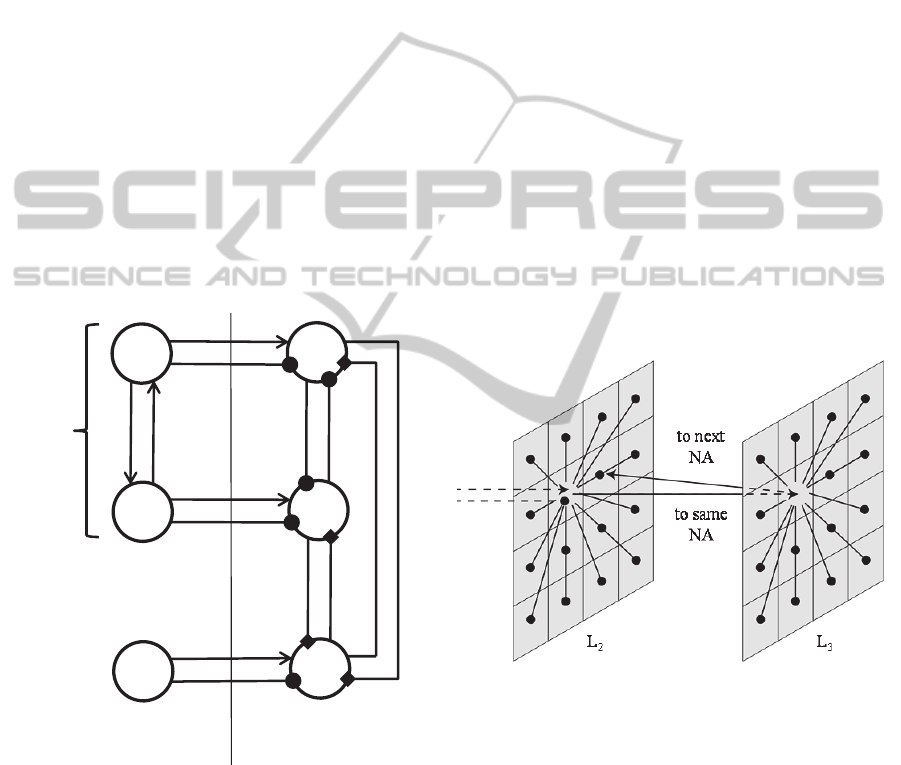
Figure 3: Connections between 6 regions, 3 in L

and 3 in

. The 4 upper regions encode for features belonging to

the same NA, while the lower 2 encode for a feature

belonging to another NA. Arrows, circles and squares

represent respectively pyramidal-pyramidal connections,

pyramidal-GABA

A,fast

connections and fast AMPA-

mediated pyramidal-GABA

A,fast

connections.

In conclusion, ultrafast anti-Hebbian synapses

from pyramidal to GABA

A,fast

neurons ensures a

very rapid desynchronization of units, while slower

Hebbian synapses from pyramidal to GABA

A,fast

neurons ensure synchronization in the gamma range.

2.3 Recall of a Sequence of Patterns

To recall patterns in a specified sequence we added a

third layer (L

) whose cortical columns are

connected in the same way as columns in L

. Units

in L

target units in L

which belong to the same

NA. On the other hand, units in L

target units in L

which belong to the next NA in the sequence (Figure

4). The connections between L

and L

are mediated

by the same synapses involved in the generation of

the gamma rhythm. These are learnt with the Hebb

rule during a training period, in which the different

patterns in a sequence are given to the network in

the correct order, delayed by 25 ms each.

Subsequently, the network is tested by providing just

the first pattern of the sequence as an input to L

Thanks to the trained synapses, when a NA pops out

in L

it pops out also in L

with a half gamma cycle

delay. In turn, a NA in L

evokes the next one in L

with the same delay. As a consequence, if the first

NA of the sequence is evoked in L

, all the other

NAs will follow with a gamma period delay each.

Figure 4: Architecture of the third layer and its

connections with L

: as in figure 2, arrows indicate

connections toward pyramidal cells, while circles indicate

connections toward GABA

A,fast

interneurons.

3 RESULTS

Figure 5 shows the behaviour of a NMM that has

learnt 7 simultaneous non sequential patterns. Note

that in L

all the NAs are activated and oscillate in

phase in the theta frequency range (4Hz in this case).

In L

the NAs are activated one at a time, but in each

theta cycle just a few (2 or 3) gamma oscillations

take place. Panel c shows that, when a NA

Same

Other

RecoveryofSequentialandNonSequentialMemorieswithaNeuralMassModel

549

completes its gamma oscillation (and thus stops

inhibiting other NAs) all the other ones compete to

start the new cycle. However, due to their mutual

inhibition, none of them prevails immediately and it

takes almost 50 ms for a new pattern to win the

competition. This delay prevents the system from

evoking more than 2-3 oscillations within a theta

cycle. All seven patterns can be recovered, but in

different theta cycles.

This observation suggests that, if at the end of a

gamma impulse one of the patterns is privileged

with respect to the other ones, the delays between

the oscillations in L

can be avoided, thus allowing

for the appearance of a greater number of gamma

impulses within a theta cycle.

Figure 5: Activity of 7 non-sequential patterns. Panels a

and b show the activity of 7 cortical columns (one for each

learnt pattern) in L

and L

respectively. Panel c shows a

zoom of the area within the dotted boundary in panel b.

Figure 6 shows that the modified network, which

learns a sequence of patterns in a well-established

order, can recover all 7 NAs within a theta cycle, in

response to the first pattern given as input. This is

due to the fact that at each gamma period one NA in

receives an additional excitation from the

previous NA in L

, thus greatly unbalancing the

competition between the different NAs to emerge.

4 CONCLUSIONS

We can draw some considerations on the results

obtained. The main point is that this modelling study

suggests a possible neural basis for an everyday

phenomenon: it is much easier to keep in mind

objects or concepts assigned in a given order, than

totally uncorrelated ones. Furthermore, the two

models can afford two alternative problems: i) to

store and recover different patterns provided

simultaneously; ii) to store and recover a sequence

of patterns, so that the first can evoke all the others

in the assigned order.

Figure 6: Activity of 7 patterns in a sequence. Panels a, b

and d show the activity of 7 cortical columns (one for each

learnt pattern) in L

, L

and L

respectively. Panels c and e

show zooms of the areas within the dotted boundaries in

panels b and d respectively.

Furthermore, the present model emphasizes the

strict relationship existing between theta and gamma

rhythms in memory storage and recall, a behaviour

which has been observed in many memory tasks,

such as during phase precession (Lisman, 2005) and

the formation of memories (Bikbaev and Manahan-

Vaughan, 2008) in the hippocampus.

A point which requires a brief discussion is the

learning capacity of the network. In this work we

0 0.5 1

Patterns in

firing rate (Hz)

0 0.5 1

Patterns in L

time (s)

firing rate (Hz)

0.1 0.15 0.2 0.25

0.5

Patterns in L

(detail)

time (s)

Column in pattern 1

Column in pattern 2

Column in pattern 3

Column in pattern 4

Column in pattern 5

Column in pattern 6

Column in pattern 7

0 0.5 1

Patterns in L

firing rate (Hz)

0 0.5 1

Patterns in L

firing rate (Hz)

0.1 0.15 0.2 0.25

Patterns in L

(detail)

Column in pattern 1

Column in pattern 2

Column in pattern 3

Column in pattern 4

Column in pattern 5

Column in pattern 6

Column in pattern 7

0 0.5 1

Patterns in L

time

(

)

firing rate (Hz)

0.1 0.15 0.2 0.25

Patterns in L

(detail)

time

(

)

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

550

trained the network with just 7 NAs, but there is no

theoretical limit to the number of NAs that can be

learnt, as long as there are enough cortical columns

to represent all features and the NAs are orthogonal.

The analysis of the network performance with non-

orthogonal NAs (i.e., with shared features) and the

comparison with other neural models for data

storage and recovery will be the subject of future

works.

A problem related to learning a longer sequence

is that the recall of the whole sequence in L

would

last more than one theta cycle; hence the following

theta cycle would begin in the midst of the previous

sequence. In this case a reset mechanism is required:

this should be realized to inhibit columns in L

and

stop the sequence when the theta cycle ends. It is

possible that dopamine plays a role in this process.

This study underlines the great value of

mathematical models as hypothesis generators, since

they allow exploration of all the mechanisms

involved, even those that are practically inaccessible

with a purely experimental approach.

REFERENCES

Bartos, M., Vida, I., Frotscher, M., Meyer, A., Monyer,

H., Geiger, J. R. P. and Jonas, P., (2002). Fast synaptic

inhibition promotes synchronized gamma oscillations

in hippocampal interneuron networks. Proceedings of

the National Academy of Sciences of the United States

of America, 99(20), 13222–13227.

Bartos, M., Vida, I. and Jonas, P., (2007). Synaptic

mechanisms of synchronized gamma oscillations in

inhibitory interneuron networks. Nature Reviews

Neuroscience, 8(1), 45–56.

Bikbaev, A. and Manahan-Vaughan, D., (2008).

Relationship of hippocampal theta and gamma

oscillations to potentiation of synaptic transmission.

Frontiers in Neuroscience, 2(1), 56–63.

Canolty, R. T., Edwards, E., Dalal, S. S., Soltani, M.,

Nagarajan, S. S., Kirsch, H. E., Berger, M. S.,

Barbaro, N. M. and Knight, R. T., (2006). High

gamma power is phase-locked to theta oscillations in

human neocortex. Science, 313(5793), 1626–1628.

Cona, F., Zavaglia, M. and Ursino, M., (2012). Binding

and segmentation via a neural mass model trained with

hebbian and anti-hebbian mechanisms. International

Journal of Neural Systems, 22(02), 1-20.

Cowan, N., (2000). The magical number 4 in short-term

memory: A reconsideration of mental storage capacity.

Behavioral and Brain Sciences, 24(01), 87–185.

Doesburg, S. M., Green, J. J., McDonald, J. J. and Ward,

L. M., (2009). Rhythms of consciousness: binocular

rivalry reveals large-scale oscillatory network

dynamics mediating visual perception. PLoS ONE,

4(7), e6142.

Lisman, J., (2005). The theta/gamma discrete phase code

occuring during the hippocampal phase precession

may be a more general brain coding scheme.

Hippocampus, 15(7), 913–922.

von der Malsburg, C. and Buhmann, J., (1992). Sensory

segmentation with coupled neural oscillators.

Biological Cybernetics, 67(3), 233–242.

Miller, G. A., (1956). The magical number seven, plus or

minus two: some limits on our capacity for processing

information. Psychological Review, 63(2), 81–97.

Singer, W., (1999). Neuronal synchrony: a versatile code

for the definition of relations. Neuron, 24, 49–65.

Ursino, M., La Cara, G. E. and Sarti, A., (2003). Binding

and segmentation of multiple objects through neural

oscillators inhibited by contour information.

Biological Cybernetics, 89(1), 56–70.

Ursino, M., Cona, F. and Zavaglia, M., (2010). The

generation of rhythms within a cortical region:

Analysis of a neural mass model. NeuroImage, 52(3),

1080–1094.

Ursino, M., Magosso, E. and Cuppini, C., (2009).

Recognition of abstract objects via neural oscillators:

Interaction among topological organization,

associative memory and gamma band synchronization.

IEEE Transactions on Neural Networks, 20(2), 316–

335.

Varela, F., Lachaux, J. P., Rodriguez, E. and Martinerie,

J., (2001). The brainweb: Phase synchronization and

large-scale integration. Nature Reviews Neuroscience,

2(4), 229–239.

Wang, D., Buhmann, J. and von der Malsburg, C., (1990).

Pattern segmentation in associative memory. Neural

Computation, 2(1), 94–106.

Wang, D. and Terman, D., (1997). Image segmentation

based on oscillatory correlation. Neural Computation,

9(4), 805–836.

RecoveryofSequentialandNonSequentialMemorieswithaNeuralMassModel

551