
Deductive Reasoning
Using Artificial Neural Networks to Simulate Preferential Reasoning
Marco Ragni and Andreas Klein
Center for Cognitive Science, Friedrichstr. 50, 79098 Freiburg, Germany
Keywords:
Knowledge Representation and Reasoning, Preferential Reasoning, Artificial Neural Networks.
Abstract:
Composition tables are used in AI for knowledge representation and to compute transitive inferences. Most of
these tables are computed by hand, i.e., there is the need to generate them automatically. Furthermore, human
preferred solutions and errors in reasoning can be explained as well based on these tables. First, we will report
briefly psychological results about the preferences in calculi. Then we show that we can train ANNs on a
simple calculus like the point algebra and the trained ANN is able to correctly solve larger calculi such as the
Cardinal Direction Calculus. As human prefer specific conclusions, we are able to show that based on the
ANN, which is trained on the preferred conclusions of the point algebra alone, is able to reproduce the results
on the larger calculi as well. Finally, we show that humans preferred solutions can be adequately described by
the networks. A brief discussion of the structure of successful ANNs conclude the paper.
1 INTRODUCTION
Consider the following problem:
(1) Ann is smaller than Beth.
Beth is smaller than Cath.
From the given premises, when asked what follows,
it is easy for most people to conclude that Ann is
smaller than Cath. Psychologists have studied prob-
lems like this, typically called three-term-series prob-
lems, for years in an attempt to determine which are
most difficult, and equally as important, why. A typ-
ical resulting dataset from such an experiment can be
thought of as a function that accepts the relationships
between the arguments of the first premise and be-
tween the arguments of the second premise and re-
turns the frequency of subjects various responses. In
contrast to the domain of the above problem, which is
one-dimensional, it is also possible to present three-
term-series problems using domains that are multi-
dimensional. Doing so allows for problems with a
much greater degree of underspecification between
the domain and codomain, such that there are many
more acceptable answers. It also happens that they
are more ecologically valid. For example, consider
the following (Ragni and Becker, 2010):
(2) Berlin is Northeast of Paris.
Paris is Northwest of Rome.
While it is possible to infer that Berlin must be North
(N) of Rome, it is not possible to determine whether
Berlin is East (E) or West (W) of Rome. As a re-
sult, it is likely that psychological preference plays a
greater role in determining the possible conclusion.
AI researchers have used a similar data structure, the
composition table, in order to efficiently represent
knowledge and compute transitive inferences (Cohn,
1997). However, the unfortunate problem with com-
position tables is that populating them with data is of-
ten painstakingly slow and likely to introduce errors,
as more often than not, these computations are done
by hand. It would be of great use to researchers in
both fields, AI and Psychology, if there were a way
to accurately approximate the values in the final table
using methods that were less resource intensive. The
current paper proposes one such method, using Artifi-
cial Neural Networks (ANNs). We begin by showing
that we can train ANNs on the Point Algebra (PA),
a one-dimensional domain, and that these ANNs are
able to correctly solve a larger and complex domain,
the Cardinal Direction (C D). Then we present a psy-
chological experiment using problems from C D and
demonstrate than an ANN trained on human prefer-
ences in PA can reproduce the table of human pref-
erence data collected in C D. Finally, we discuss the
structure of the ANNs.
635
Ragni M. and Klein A..
Deductive Reasoning - Using Artificial Neural Networks to Simulate Preferential Reasoning.
DOI: 10.5220/0004155106350638
In Proceedings of the 4th International Joint Conference on Computational Intelligence (NCTA-2012), pages 635-638
ISBN: 978-989-8565-33-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
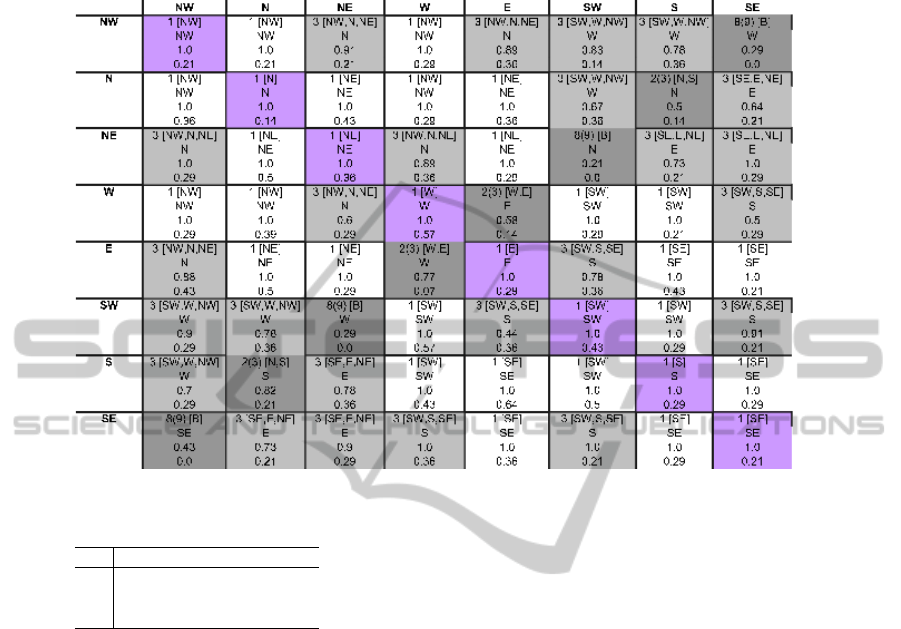
Table 1: The preferred relations in reasoning with cardinal direction taken from (Ragni and Becker, 2010). The first line in
each cell contains the number of and all possible relations, the second line the preferred relation, the third the percentage of
participants who chose this relation. The grey/white shaded cells are the multiple/single solution cells.
Table 2: Composition table for the Point Algebra (PA),
where < encodes left of, = equal to, and > right of.
< = >
< < < <, =, >
= < = >
> <, =, > > >
2 STATE-OF-THE-ART
For example, consider the domain of possible rela-
tionships between two points in one dimension, e.g.
R. This domain is typically referred to as the Point Al-
gebra (PA). Within PA , it always holds that between
two points, there are only three possible relationships,
at least one of which always holds: A can be either left
of ( <), equal to (=), or right of (>) a second point B.
The PA, and many other domains like it, can be pre-
sented in the form of a composition table (cf. Table
2). Transitive inferences can be represented in com-
position tables (Bennett et al., 1997). Using a set of
three points a composition table can be constructed,
depicting the relations between them (cf. Table 2).
For instance, point A is left of point B, A < B (left col-
umn), and B is left of point C, B < C (first row), then
point A can only be left of point C, A < C (entry in
second column, second row). The cardinal direction
calculus C D consists of 9 base relations (N = north, E
= east, S = south, W = west and combinations such as
NE = north-east). The points in the euclidean plane
can be expressed by relations of PA-algebra: The re-
lation of two points z
1
Nz
2
can be described by x
1
= x
2
and y
1
> y
2
for z ∈ R
2
with z
i
= (x
i
, y
i
). Analogously,
NW by (>,>) and so on. An interesting finding is
that humans do not consider all possible models but
that there is a so-called preference effect, i.e., in mul-
tiple model cases (nearly always) one preferred model
is constructed from participants and used as a refer-
ence for the deduction process (Rauh et al., 2005). In
a previous experiment (Ragni and Becker, 2010) the
participants received premises (like problem (2) but
with letters instead of real cities) and their task was to
give a relation that holds between the first and the last
term. Similar to the point algebra above these prob-
lems can be formally described by the composition
of two base relations and the question for satisfiable
relations (cf. Table 1). For the above example NE
and NW contains the following three relations: NE,
N, NW. If we omit all one-relation cases (cells with
one entry in Table 1), it results in 40 multiple relation
cases out of the 64 possible compositions. The partic-
ipants in (Ragni and Becker, 2010) were confronted
with all 64 problems and had to infer a conclusion –
showing clear preference effects.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
636

3 PROVOKING PREFERENCES
In order to make an ANN learn the PA the first step
is to find a suitable encoding for the specified rela-
tions and an architecture of the ANN for the consid-
ered kind of problem. Since the problems considered
here are 3-term problems, an architecture with two
nodes in the input layer were used for classifying pos-
sible relations. For the encoding of the premises, −1
was used for the relation <, 0 for =, and 1 for >. For
this kind of problems it is possible, that all three rela-
tions hold between two points. Therefor, three nodes
within the output layer were used. Respectively one
for each possible relation. If a relation holds for given
premises, the corresponding output node returns 1,
else it returns 0. For example, the premises [−1, 0]
with the target output [1, 0, 0] is a suitable pattern for
training the ANN. It represents the three-term-series
problem with the premises a<b, b=c and the solution
a<c. Furthermore, a hidden layer was used and the
number of nodes iteratively increased to find a suc-
cessful architecture for the given problem. For train-
ing the ANN, backpropagation was used as learning
algorithm with 1000 training iterations, a learning rate
of .3 and a momentum factor of .1. The tangens hy-
perbolicus was used as sigmoid activation function.
As depicted in Table 3, a suitable architecture requires
six nodes within the hidden layer. Since the ANN
Table 3: Rounded results on training different ANN archi-
tectures for PA. (hn = number of hidden nodes).
Prem 1 hn 2 hn 3 hn 4 hn 5 hn 6 hn 7 hn
p
1
p
2
<, =, ><, =, ><, =, ><, =, ><, =, ><, =, ><, =, >
-1 -1 1,0,1 1,0,0 1,-1,-1 1,0,0 1,1,0 1,0,0 1,0,0
-1 0 1,0,1 1,0,0 1,1,0 1,0,0 1,1,0 1,0,0 1,0,0
-1 1 1,0,1 1,0,1 1,1,1 1,1,1 1,1,1 1,1,1 1,1,1
0 -1 1,0,1 1,0,0 1,0,0 1,0,0 1,1,0 1,0,0 1,0,0
0 0 1,0,1 1,0,1 1,1,0 1,1,1 0,1,0 0,1,0 0,1,0
0 1 0,0,1 0,0,1 0,0,1 0,0,1 0,0,1 0,0,1 0,0,1
1 -1 1,0,1 1,0,1 1,1,1 1,1,1 1,1,1 1,1,1 1,1,1
1 0 0,0,1 0,0,1 0,0,1 0,0,1 0,0,1 0,0,1 0,0,1
1 1 0,0,0 0,0,1 0,0,1 0,0,1 0,0,1 0,0,1 0,0,1
Errors 3.685 1.980 1.260 0.766 1.503 0.020 0.086
was trained on the complete set of correct patterns of
three-term-series problems of PA, it is some kind of
over-fitted. However, in this case this does not matter,
because the ANN is only used to provide real-valued
outcomes in the complete process to determine possi-
ble sources for preferences. For this purpose, the tar-
get values will be varied from integers to real-values
to reproduce preferences in PA reasoning. The re-
sult shows that PA is learnable by a quite small ANN
with little effort and suggests a good architecture of
an ANN for this kind of task. Human reasoning per-
Table 4: Mapping of C D relations to ANN input. Re-
sults on training the ANN with the varied patterns [[-1,
1],[0.9,1,0.9]] and [[ 1,-1],[0.9,1,0.9]] of PA.
C D PA ANN Learned Target
Rel. Dimension Input Values
x y x y
SW < < -1 -1 0.990 -0.360 0.107
W < = -1 0 0.999 -0.410 0.092
NW < > -1 1 0.902 0.970 0.897
S = < 0 -1 0.987 -0.327 0.040
EQ = = 0 0 -0.003 0.998 0.004
N = > 0 1 0.000 -0.003 1.000
NE > < 1 -1 0.902 0.996 0.884
E > = 1 0 0.000 0.000 1.000
SE > > 1 1 0.000 0.000 1.000
formance is known to be error prone and in cases of
various solutions preferences for particular relations
can be found (Rauh et al., 2005). In the previous sub-
section it was shown that an ANN is basically able to
learn PA . But what happens if the level of believe,
i.e., the target values in the patterns, change? For the
perfect fitting of the previous described ANN the fol-
lowing patterns were used:
[[-1,-1],[1,0,0]],
[[-1, 0],[1,0,0]],
[[-1, 1],[1,1,1]], (1)
[[ 0,-1],[1,0,0]],
[[ 0, 0],[0,1,0]],
[[ 0, 1],[0,0,1]],
[[ 1,-1],[1,1,1]], (2)
[[ 1, 0],[0,0,1]],
and [[ 1, 1],[0,0,1]]. And a variation of some target
values, i.e.
[[-1, 1],[0.9,1,0.9]], (1)
[[ 1,-1],[0.9,1,0.9]], (2)
used in the latter for Cardinal Directions problems,
changes the rounded results shown in Table 3 in the
way the reported preferences of humans suggest. Ta-
ble 4 depicts the outcoming results for both of this
changes by reasoning with PA with the previous de-
scribed ANN with six nodes within the hidden layer.
With a mapping for a two–dimensional C D relation
to two one–dimensional PA relations, the previous re-
sults could be used to pass preferences from one cal-
culus to the other. Considering 3ts-problems in PA
the previously described ANN is used to compute the
possible relation for a given problem. Now, for 3ts-
problems in C D the relations must be split by their x–
and y–dimensions and computed separately. To com-
pute the PA outcome only one ANN is used. Given
z
1
q
1,2
(x, y)z
2
:= z
1
r
1,2
(x)z
2
∧z
1
r
1,2
(y)z
2
, with q
1,2
∈
C D and r
1,2
∈ PA , and z
2
q
2,3
(x, y)z
3
:= z
2
r
2,3
(x)z
3
∧
z
2
r
2,3
(y)z
3
, with q
2,3
∈ C D and r
2,3
∈ PA the in-
puts for the ANN are r
1,2
(x) and r
2,3
(x) for the x–
dimensional information specified in the problem,
and r
1,2
(y) and r
2,3
(y) for the y–dimensional infor-
mation. The mapping of the C D relation is given
in Table 4. The result of the ANN concerning
DeductiveReasoning-UsingArtificialNeuralNetworkstoSimulatePreferentialReasoning
637

Table 5: Mapping from the two ANNs output back to C D .
0,0,1 0,1,0 1,0,0 1,1,1
0,0,1 NE E SE SE,E,NE
0,1,0 N EQ S S,EQ,N
1,0,0 NW W SW SW,W,NW
1,1,1 NW,N,NE W,EQ,E SW,S,SE All
the x-dimension is given by ANN
x
(r
1,2
(x), r
2,3
(x)) =
(r
1,3
(x)
1
∨ r
1,3
(x)
2
∨ r
1,3
(x)
3
) with r
1,3
(x)
i
∈ B and
i ∈ {1, 2, 3}, where i = 1 is interpreted as western,
i = 2 as equal to, and i = 3 as eastern if the out-
come for the corresponding index is true. The ana-
log hold for the ANN if concerning the y-dimension,
but the boolean outcome i = 1 is interpreted as
southern, i = 2 as equal to, and i = 3 as north-
ern. In a last step the two PA results are mapped
back to one C D result set by recombining the x–
and y–dimension results. Therefor, the combina-
tion ANN
x
(r
1,2
(x), r
2,3
(x)) × ANN
y
(r
1,2
(y), r
2,3
(y)) =
((r
1,3
(x)
1
∧ r
1,3
(y)
1
) ∨ (r
1,3
(x)
1
∧ r
1,3
(y)
2
) ∨ . . . ∨
(r
1,3
(y)
3
∨ r
1,3
(x)
3
)) is computed. Table 5 depicts the
mapping back from the two ANN output sets to C D
relation sets. With the ANN correctly trained for PA
the outcomes (0,0,0), (0,1,1), (1,0,1), and (1,1,0) are
never generated and would reflect errors in PA. Using
an ANN trained to PA without variations of training
patterns, as shown above, this procedure reproduces
the composition table for C D perfectly, but only 47
of the human preferences. Using the training patterns
the ANN predicts 56 of the 64 preferred relations (cp.
Table 1 and Table 6).
Table 6: The generated preferences for C D, trained with the
variation [[-1, 1],[0.9,1,0.9]] and [[ 1,-1],[0.9,1,0.9]] on the
PA. 56 out of 64 are correctly predicted.
E N NE NW S SE SW W
E E
(1.0)
NE
(1.0)
NE
(1.0)
N
(1.0)
SE
(0.99)
SE
(0.99)
S
(0.99)
EQ
(1.0)
N NE
(1.0)
N
(1.0)
NE
(1.0)
NW
(0.99)
EQ
(1.0)
E
(1.0)
W
(0.99)
NW
(0.99)
NE NE
(1.0)
NE
(1.0)
NE
(1.0)
N
(1.0)
E
(1.0)
E
(1.0)
EQ
(1.0)
N
(1.0)
NW N
(0.98)
NW
(1.0)
N
(0.98)
NW
(0.99)
W
(1.0)
EQ
(0.98)
W
(0.99)
NW
(0.99)
S SE
(1.0)
EQ
(0.98)
E
(0.98)
W
(0.98)
S
(0.99)
SE
(0.99)
SW
(0.99)
SW
(0.99)
SE SE
(1.0)
E
(0.98)
E
(0.98)
EQ
(0.98)
SE
(0.99)
SE
(0.99)
S
(0.99)
S
(1.0)
SW S
(0.98)
W
(0.98)
EQ
(0.97)
W
(0.98)
SW
(0.99)
S
(0.98)
SW
(0.99)
SW
(0.99)
W EQ
(0.98)
NW
(1.0)
N
(0.98)
NW
(0.99)
SW
(0.99)
S
(0.98)
SW
(0.99)
W
(0.99)
4 CONCLUSIONS
Composition tables are central in the fields of knowl-
edge representation and reasoning in dealing with in-
ferences in qualitative calculi. They are both impor-
tant for Artificial Intelligence, which uses them to
check the consistency of a network (Bennett et al.,
1997), and human reasoning, which describes reason-
ing errors by wrong preferred relations (Rauh et al.,
2005). So far about all composition tables had been
generated by hand. The problem becomes relevant
with increasing calculi as the tables become much
more difficult to compute. We could explain human
preferred relations of complex calculi, like cardinal
directions by preferences in the point algebra. The
correct preferences of 56 of 64 (87,5%) of C D could
be correctly reproduced. The problem of selecting
an adequate neural network architecture for a given
problem has become recently more and more in the
research focus (Franco, 2006). Here best fitting neu-
ral networks could be identified, which reproduce the
correct composition tables and human preferences.
An analysis shows that 6 hidden nodes provide the
best fitting architecture for this approach. The de-
scribed method seems fruitful for both formal and
psychological reasoning.
REFERENCES
Bennett, B., Isli, A., and Cohn, A. G. (1997). When does
a composition table provide a complete and tractable
proof procedure for a relational constraint language?
In Proceedings of the IJCAI97 Workshop on Spatial
and Temporal Reasoning, Nagoya, Japan.
Cohn, A. G. (1997). Qualitative spatial representation and
reasoning techniques. In Brewka, G., Habel, C., and
Nebel, B., editors, KI-97: Advances in Artificial Intel-
ligence, Berlin, Germany. Springer-Verlag.
Franco, L. (2006). Generalization ability of boolean func-
tions implemented in feedforward neural networks.
Neurocomputing, 70:351–361.
Ragni, M. and Becker, B. (2010). Preferences in cardinal
direction. In Ohlsson, S. and Catrambone, R., edi-
tors, Proc. of the 32nd Cognitive Science Conference,
pages 660–666, Austin, TX.
Rauh, R., Hagen, C., Knauff, M., Kuss, T., Schlieder, C.,
and Strube, G. (2005). Preferred and Alternative Men-
tal Models in Spatial Reasoning. Spatial Cognition
and Computation, 5.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
638
