
Using Self-organized Criticality for Adjusting the Parameters of a
Particle Swarm
Carlos M. Fernandes, Juan Julián Merelo
Department of Computers’ Architecture, University of Granada, Granada, Spain
Agostinho C. Rosa
Department of Electrotechnics, Technical University of Lisbon, Lisbon, Portugal
Keywords: Particle Swarm Optimization, Self-organized Criticality, Parameter Control.
Abstract: The local and global behavior of Self-Organized Criticality (SOC) systems may be an efficient source for
controlling the parameters of a Particle Swarm Optimization (PSO) without hand-tuning. This paper
proposes a strategy based on the SOC Bak-Sneppen model of co-evolution for adjusting the inertia weight
and the acceleration coefficients values of the PSO. In order to increase exploration, the model is also used
to perturb the position of the particles. The resulting algorithm is named Bak-Sneppen PSO (BS-PSO). An
experimental setup compares the new algorithm with versions of the PSO with varying inertia weight,
including a state-of-the-art algorithm with dynamic variation of the weight value and perturbation of the
particles’ positions. The parameter values generated by the model are investigated in order to understand the
dynamic of the algorithm and explain its performance.
1 INTRODUCTION
The Particle Swarm Optimization (PSO) algorithm
is a meta-heuristic for binary and real-valued
function optimization inspired by the social behavior
of organisms in bird flocks and fish schools
(Kennedy and Eberhart, 1995). Since its inception,
PSO has been applied with success to a number of
problems and motivated several lines of research
that investigate its working mechanisms. One of
these research lines studies the parameters of the
algorithm, namely, the acceleration coefficients and
the inertia weight, which control the balance
between global and local search.
As in other population-based metaheuristics, the
parameter values of PSO may be hand-tuned for
optimal performance or adjusted during the run.
There are different types of strategies for varying the
parameters during the run: deterministic (the values
change according to pre-defined rules), adaptive (the
values depend on the state of the search) or self-
adaptive (the parameters evolve with the solutions)
— see (Eiben et al., 1999) for a review on parameter
control strategies. Self-Organized Criticality (SOC)
theory, first described in (Bak et al., 1987), provides
interesting schemes that can be easily tailored for
deterministic and adaptive control of PSO’s working
mechanisms. In fact, SOC has been used in the past
in population-based metaheuristics, like
Evolutionary Algorithms — see, for instance,
(Fernandes et al, 2008) and (Krink et al., 2001) —
and even PSO (Løvbjerg and Krink, 2002). In this
paper we propose a versatile method inspired by the
SOC theory for controlling the parameters of PSO.
The new control strategy is not deterministic in
the strict sense, due to its stochastic nature (although
with a predictable global behavior) and dependence
on the swarm’s size; in addition, depending on the
way it is implemented and on the degree of
hybridization between the model and the PSO, it
may be adaptive or even self-adaptive. This paper
investigates the potentiality of the proposed method
as a stochastic seed for varying the parameters,
postponing a study of a stronger hybridization of the
SOC model and the PSO for a future work.
The algorithm is based on a SOC system known
as the Bak-Sneppen model of co-evolution between
interacting species (Bak and Sneppen, 1993). The
resulting algorithm, called Bak-Sneppen PSO (BS-
62
M. Fernandes C., Merelo J. and C. Rosa A..
Using Self-organized Criticality for Adjusting the Parameters of a Particle Swarm.
DOI: 10.5220/0004158200620071
In Proceedings of the 4th International Joint Conference on Computational Intelligence (ECTA-2012), pages 62-71
ISBN: 978-989-8565-33-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

PSO), uses the fitness values of the population of co-
evolving species, since the dynamics of these values
provides a promising basis for controlling PSO’s
parameters. Therefore, we investigate the efficiency
of the fitness as control values of the inertia weight
and acceleration coefficients. Furthermore, the exact
same fitness values are used for perturbing the
positions of the particles, thus introducing a kind of
mutation in PSO.
A simple experimental setup was designed as a
proof-of-concept. BS-PSO is compared with
deterministic and adaptive control methods, as well
as with a state-of-the-art PSO that adapts the inertia
weight values and introduces perturbations in the
particles’ positions. Two different topologies for the
population networks are considered. The tests are
conducted in a way such that each new component
of BS-PSO is examined separately in order to
investigate its effects on the performance of the
algorithm. The results demonstrate the validity of
the approach and show that BS-PSO, without
requiring the hand-tuning of the inertia weight or
acceleration coefficients, is competitive with other
PSOs. Furthermore, the base-model is simple and
well-studied by the SOC theory, and may be treated
as a black-box system that outputs batches of values
for the parameters.
The present work is organized as follows. The
next section describes PSO; Section 3 introduces
SOC and gives some examples of the application of
this theory in bio-inspired computation; Section 4
describes the proposed BS-PSO; Section 5 describes
the experiments and discusses the results. Finally,
Section 6 concludes the paper and outlines future
lines of research.
2 PARTICLE SWARM
OPTIMIZATION
The PSO algorithm is a swarm intelligence
algorithm in which a group of solutions travels
through the search space according to a set of rules
that favor their movement towards optimal regions
of the space. A simple set of equations that define
the velocity and position of each particle. The
position vector of the i-th particle is given by
,
,
,
,…
,
), where is the dimension of
the search space. The velocity is given by
,
,
,
,…
,
). The particles are evaluated with a
fitness function
in each time step and then
their velocities and positions are updated by:
,
,
1
,
,
1
,
,
1
(1)
,
,
1
,
(2)
where
is the best solution found so far by particle
,
is the best solution found so far by the
neighborhood,
and
are vectors of random
numbers uniformly distributed in the range 0,1] and
and
are acceleration coefficients that tune the
relative influence of each term of the formula. The
first, influenced by the particles best solution, is
known as the cognitive part, since it relies on the
particle’s own experience. The last term is the social
part, since it describes the influence of the
community in the velocity of the particle.
Two typical sociometric principles may define
the population network structure, which defines
neighborhood of each particle, although other
structures are possible. The first connects all the
members of the swarm to one another. It is called
, where stands for global. The second,
called (stands for local), creates a
neighborhood that comprises the particle itself and
its nearest neighbors. In order to prevent particles
from stepping out of the limits of the search space,
the positions
,
of the particles are limited by
constants that, in general, correspond to the domain
of the problem:
,
∊
,
. Velocity
may also be limited within a range in order to
prevent the explosion of the velocity vector:
,
∊
,
.
Although the basic PSO may be very efficient on
numerical optimization, it requires a proper balance
between local and global search. If we look at
equation 1, we see that the last term on the right-
hand side of the formula provides the particle with
global search abilities, while the first and second
terms act as a local search mechanism. Therefore, by
weighting these two parts of the formula it is
possible to balance local and global search. In order
to achieve a balancing mechanism, Shi and Eberhart,
(1998) introduced the inertia weight , which is
adjusted — usually within the range [0, 1.0] —
together with the constants
and
in order to
achieve the desired balance. The modified velocity
equation is:
,
,
1
,
,
1
,
,
1
(3)
The parameter may be used as a constant that is
defined after an empirical investigation of the
algorithm’s behaviour. Another possible strategy,
UsingSelf-organizedCriticalityforAdjustingtheParametersofaParticleSwarm
63

introduced in (Shi and Eberhart, 1999), is to use
time-varying inertia weights (TVIW-PSO): starting
with an initial and pre-defined value, the parameter
value decreases linearly with time, until it reaches
the minimum value. Later, Eberhart and Shi (2000)
found that the TVIW-PSO is not very effective on
dynamic environments and proposed a random
inertia weight for tracking dynamic systems. In the
remainder of this paper, this method is referred to as
RANDIW-PSO.
An adaptive approach is proposed in (Arumugam
and Rao, 2006). The authors describe a global local
best inertia weight PSO (GLbestIW-PSO), which
uses an on-line variation strategy that depends on the
and
values. The strategy is defined in a way
that better solutions use lower inertia weight values,
thus increasing their local search abilities. The worst
particles are modified with higher values and
therefore tend to explore the search space.
Ratnaweera et al. (2004) describe new parameter
automation strategies that act upon several working
mechanisms of the algorithm. The authors propose
the concept of time-varying acceleration
coefficients. They also introduce the concept of
mutation, by adding perturbations to randomly
selected modulus of the velocity vector. Finally, the
authors describe a self-organizing hierarchical
particle swarm optimizer with time-varying
acceleration coefficients (HPSO-TVAC), which
restricts the velocity update policy to the influence
of the cognitive and social part, reinitializing the
particles whenever they are stagnated in the search
space. Ratnaweera et al. show that the HPSO-TVAC
outperforms other methods in a specific test set.
Another method for controlling is given by
Suresh et al. (2008): the inertia-Adaptive PSO (IA-
PSO). The authors use the Euclidean distance
between the particle and for computing in
each time-step for each particle. Particles closer to
the best global solution tend to have higher
values, while particles far from are modified
with lower inertia. The algorithm introduces a
parameter
that restricts the inertia weight to
working values. In addition, Suresh et al. also uses a
perturbation mechanism of the particles’ positions
that introduces a random value in the range 1,,
where is a new parameter for the algorithm (see
equation 4, which replaces equation 2). The authors
report that the IA-PSO outperforms several other
methods in a 12-function benchmark, including the
above referred state-of-the-art HPSO-TVAC. The
algorithm is simple and easy to implement and it
was included in the test set described in Section 4 in
order to evaluate the performance of the BS-PSO.
,
1
.
,
1
,
(4)
Like HPSO-.TVAC and IA-PSO, the method
proposed in this paper also aims at controlling the
balance between local and global search by
dynamically varying the parameters, while
introducing perturbations in the particles’ positions
(like IA-PSO, but with
controlled by the SOC
model)
. The main objective is to construct a simple
scheme that does not require complex parameter
tuning or pre-established strategies. In addition, each
particle’s inertia weight, acceleration coefficients
and perturbation
are controlled by the same
species of the BakSneppen model, which simplifies
the algorithm’s design and links the four parameters
to a common variation strategy. Section 3 describes
SOC, the Bak-Sneppen model and new method for
controlling the parameters.
3 SELF-ORGANIZED
CRITICALITY
SOC systems are dynamical system with a critical
point in the transition region between order and
chaos as an attractor. While order means that the
system is working in a predictable regime where
small disturbances have only local impact, chaos is
an unpredictable state very sensitive to initial
conditions or small disturbances. In complex
adaptive systems, complexity and self-organization
usually arise in that region. However, and unlike
many physical systems, which have a parameter that
needs to be tuned in order to reach criticality, SOC
systems are able to self-tune to that critical state.
Small disturbances in a SOC system that is in the
critical state can lead to the so-called avalanches,
i.e., chain reactions that are spatially or temporally
spread through the system. This happens
independently of the initial state. Moreover, the
same perturbation may lead to small or large
avalanches, which in the end show a power-law
proportion between their size and abundance. This
means that large events may hit the system
periodically and reconfigure it.
The first model in which SOC was identified was
the sandpile model, introduced by Bak et al. (1987).
Later, another SOC model was devised in order to
describe the relationship between extinction events
and their frequencies, and explain some features of
the fossil record. The system is named after the
scientists who first described it as the Bak-Sneppen
model (Bak and Sneppen, 1993).
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
64

The Bak-Sneppen is a model of co-evolution
between interacting species in an ecological
environment. Different species in the same eco-
system are related through several features (food
chains, for instance); they co-evolve, and the
extinction of one species affects the other species
that are related to it, in a chain reaction that can
affect large segments of the population. Each species
has a fitness value assigned to it and it is connected
to other species (neighbors) in a ring topology (i.e.,
each species has two neighbors). Every time step,
the species with the worst fitness and its neighbors
are eliminated from the system and replaced by
individuals with random fitness. Such an event is
recorded as an avalanche of size1; if the next
mutation involves one of the newly created species,
then the size is incremented. When plotting the size
of the extinctions over their frequency in a local
segment of the population and below a certain
threshold close to a critical value, a power-law
behavior is observed.
This description may be translated to a
mathematical model. The system is defined by
fitness numbers
arranged on a -dimensional
lattice (ecosystem) with cells. At each time step,
the smallest value and its 2 neighbours are
replaced by uncorrelated random values drawn from
a uniform distribution. The system is thus driven to a
critical state where most species have reached a
fitness value above a certain threshold. The
coevolutionary activity gives rise to chain reactions
or avalanches: large (non-equilibrium) fluctuations
in the configuration of the fitness values that
rearrange major parts of the system.
The dynamics of the numerical values of the
Bak-Sneppen model — power-law relationships
between mutation events and their frequency,
increasing average fitness of the population, periods
of stasis in segments of the population punctuated by
intense activity — are the motivation behind the
investigation described in this paper. By linking a
Bak-Sneppen model to the population of the PSO
and then using the species’ fitness values as input for
controlling the algorithm’s parameters, it is expected
that the resulting strategy is able to control the
inertia weight of the algorithm. To the extent of our
knowledge, this is the first proposal of a scheme
linking the Bak-Sneppen model and PSO in such a
way. However, SOC has been applied to this field of
research in the past.
Proposed by Boettcher and Percus (2003),
Extremal Optimization is a computational paradigm
for numerical optimization based on the Bak-
Sneppen model. Extremal Optimization does not
work with a population of individuals; instead it
evolves a single solution to the problem by local
search and modification. The algorithm removes the
worst components of the solution and replaces them
with randomly generated material. By plotting the
fitness of the solution, it is possible to observe
distinct stages of evolution, where improvement is
disturbed by brief periods of dramatic decrease in
the quality of the solution.
In the Evolutionary Algorithms research field,
Krink et al. (2001) proposed SOC-based mass
extinction and mutation operator schemes — later
extended to cellular GAs (Krink et al., 2002). The
sandpile equations are previously computed in order
to obtain a record of values with a power-law
relationship. Those values are then used during the
run to control the number of individuals that will be
replaced by randomly generated solutions (SOC
mass extinction model) or the mutation probability
of the Evolutionary Algorithm (SOC mutation
model).
Tinós and Yang (2007) were also inspired by the
Bak-Sneppen model to create a sophisticated
Random Immigrants Genetic Algorithm (RIGA)
(Grefenstette, 1992), called Self-Organized Random
Immigrants GA (SORIGA). The authors apply the
algorithm to time-varying fitness landscapes and
claim that SORIGA is able to outperform other
Genetic Algorithm in the proposed test set. By
plotting the extent of extinction events (individuals
replaced by random solutions), the authors argue
that the model exhibits SOC behavior, that is, there
is a power-law proportion between the size of the
extinction events and their frequency. This means
that from time to time the population is almost
completely replaced by random immigrants.
Fernandes et al. (2008) describe an Evolutionary
Algorithm attached to a sandpile model. Later
(Fernandes et al, 2011), the system was improved
and its working mechanisms were studied. The
model evolves along with the algorithm and its
avalanches – system’s reaction events to
perturbations, which show a power-law relationship
between their size and their frequency – dynamically
control the algorithm’s mutation operator with
simple local rules. The authors use the proposed
scheme for optimizing time-varying fitness functions
and claim that the sandpile mutation Genetic
Algorithm is able to outperform other state-of-the-art
methods in a wide range of dynamic problems.
Finally, Løvbjerg and Krink (2002) apply SOC
to PSO in order to control the convergence of the
algorithm and add diversity to the population. The
authors introduce a critical value associated with
UsingSelf-organizedCriticalityforAdjustingtheParametersofaParticleSwarm
65

each particle and define a rule that increments that
value when two particles are closer than a threshold
distance. When the critical value of a particle
exceeds a globally set criticality limit, the algorithm
responds by dispersing the criticality of the particle
within a certain surrounding neighborhood and also
by mutating the particle (i.e., the particle is
“relocated”). In addition, the algorithm uses the
particle’s critical value to control the inertia weight.
The authors claim that their method is faster and
attains better solutions than the standard PSO.
However, the algorithm introduces some parameters
and working mechanisms that can complicate the
design of the PSO. Overall, there are five parameters
that must be tuned or set to constant ad hoc values.
BS-PSO does not add parameters to the basic
PSO, excepting an upper limit for the size of the
avalanches, a practical limitation due to the nature of
the Bak-Sneppen model and the requirements of a
numerical optimization algorithm. Section 4
describes this and other features of BS-PSO.
4 THE BAK-SNEPPEN PARTICLE
SWARM
BS-PSO uses a Bak-Sneppen model without
modifying any of its rules and underlying structure,
or introducing complex control mechanisms and
rules. The only exception is an upper limit for the
size of the mutation events that are allowed during a
time-step of the main PSO algorithm. This limit is
used in order to avoid long cycles of mutations in
the end of the runs that could compromise the speed
of convergence of the algorithm. Besides that, the
model is executed in its original form, during the run
of the PSO, feeding the later with values between 0
and 1.0 (the species’ fitness values) that are then
used by the algorithm to control the parameters.
Please note that if PSO does not interact directly
with the model — which is the case studied in this
paper —, the Bak-Sneppen model can be executed
prior to the optimization process and its fitness
values stored in order for them to be used later in
any kind of problem. However, in order to
generalize the system and describe a framework that
can easily be adapted to another level of
hybridization of the SOC model and the PSO, the
description of the BS-PSO in this section assumes
that the model evolves on-line with the swarm.
(Furthermore, an offline approach could require
too much memory when applied to problems that
demand large populations and long running times.)
Algorithm 1: Bak-sneppen model.
1. Set 0;set_ 2
_
2. Findtheindexofthespecieswithlowestbak‐
sneppenfitness
3. Set _
4. Replacethefitnessofindividualswithindices,
1,and1byrandomvaluesintherange
[0,1.0]
5. Incrementmutations:
6. Findtheindexofthespecieswithlowestfitness
7. If
_
or
_
,returnto4;else,end
Algorithm 2: BS-PSO.
1. Initializevelocityandpositionofeachparticle.
2. Evaluateeachparticle:
3. Initialize bak‐sneppen fitness values:
_
0,1.0
4. UpdateBak‐SneppenModel(Algorithm1).
5. Foreachparticle:
6. Set1_
7. Set
1_
8. Update velocity (equation 3) and position
(equation7)
9. If(stopcriterianotmet)returnto4;else,end.
In the Bak-Sneppen model a population of
individuals (species) is placed in a ring topology and
a random real number (between 0 and 1.0) is
assigned to each individual. In the BS-PSO, the size
of this ecosystem (number of species) is equal to the
size of the swarm. Therefore, the algorithm may be
implemented just by assigning a second (random)
fitness value, called bak-sneppen fitness value
(bs_fitness) to each individual in the swarm. This
way, each individual is both the particle of the PSO
and the species of the co-evolutionary model, with
two independent fitness values: the quality measure
fitness value
, computed as usual by the
objective function, and the bak-sneppen fitness value
, which is modified according to Algorithm 1.
The main body of the BS-PSO is very similar to
the basic algorithm. The differences are: the
algorithm 1 is called in each time-step, modifying
three or more bak-sneppen fitness values; the inertia
weight of each particle is defined in each time-step
(and for each particle ) using equation 5, where
is the vector (position) of particle ; the acceleration
coefficients
and
are defined in each time-step
by equation 6; the particles’ positions are updated
with equation 7, where
is a random value in
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
66

the range [0,1_
.
1_
(5)
1_
(6)
,
1
.
,
1
,
(7)
Algorithm 1 is executed in each time-step of the BS-
PSO. At 0, the bak-sneppen fitness values are
randomly drawn from a uniform distribution in the
range 0,0.1. Then, the algorithm searches for the
worst individual in the population (lowest
bs_fitness), stores its fitness value (minFit) and
mutates that individual by replacing the bs_fitness
by a random uniformly distributed value in the range
0,0.1
. In addition, the neighbors of the worst
species are also mutated (please remember that a
ring topology connects the population and each
species with index to its two neighbors with
indexes 1 and 1). Then, the algorithm
searches again for the current worst individual. If the
fitness of that individual is lower than minFit, the
process repeats: the individual and its neighbors are
mutated. This cycle proceeds while the worst fitness
in the population is bellow the minFit value. When
the worst fitness is found to be above minFit, the
algorithm proceeds to the standard procedures of the
basic PSO (see Algorithms 1 and 2).
As stated above, a stop criterion was introduced
in Algorithm 1, in order to avoid long mutation
cycles that would slow down the BS-PSO after a
certain number of iterations. If the number of
mutation events reaches a maximum pre-defined
value, Algorithm 1 ends (until the next time-step,
when it proceeds from the point where it stopped).
In this paper, the critical value was set to twice the
swarm’s size. This value was intuitively fixed, not
tuned for optimization of the performance. It is
treated as a constant and a study of its effects on the
performance is beyond the scope of this study. It is
even possible that other strategies for avoiding long
intra-time-steps mutation cycles can be devised that
not require a constant. However, such an
investigation is left for a future work. This paper’s
main objective is to demonstrate that a control of the
inertia weight, acceleration coefficients and
particles’ positions with values given by a SOC
model is viable and effective. For that purpose, a
classical experimental setup was prepared in order to
test the algorithm and compare it to other strategies.
The results are given in the following section, as
well a brief inspection of BS-PSO’s dynamics.
5 EXPERIMENTS
In order to test BS-PSO and compare it to other
PSOs, an experimental setup was constructed with
four unimodal and multimodal benchmark functions
that are commonly used for investigating the
performance of this class of algorithms. The
functions are described in Table 1. The optimum
(minimum) of all functions is located in the origin
with fitness 0. The dimension of the search space is
set to 30. TVIW-PSO, RANDIW- PSO,
GLbestIW-PSO and IA-PSO were included in the
tests in order to evaluate the performance of the BS-
PSO. This experiment is mainly a proof-of-concept,
and the peer-algorithms were chosen so that the
different mechanism of BS-PSO can be properly
evaluated.
The population size is set to 20 for all
algorithms two topologies for the population
network are tested: and . The
acceleration coefficients were set to 1.494, as
suggested in (Eberhart and Shi, 2000) for RANDIW-
PSO. However, since the value proposed in (Suresh
et al., 2008) and (Arumugam and Rao, 2006) for IA-
PSO and GLbestIW-PSO is 2.0, coefficients were
also set to this value. is defined as usual by
the domain’s upper limit and .
TVIW-PSO uses linearly decreasing inertia weight,
from 0.9 to 0.4. The maximum number of
generations is 3000 and a total of 50 runs for each
experiment are conducted. Asymmetrical
initialization was used (the initialization range for
each function is given in Table 1).
Table 1: Benchmarks for experiments. Dynamic and
initialization range.
mathematicalrepresentation
Rangeofsearch
Rangeof
initialization
100,100
(50,100
100
1
100,100
15,30
10cos
2
10
10,10
2.56,5.12
1
1
4000
cos
√
300,600
The first test compares versions of BS-PSO with
different degrees of parameter control (i.e., the
acceleration coefficients control and the particles’
UsingSelf-organizedCriticalityforAdjustingtheParametersofaParticleSwarm
67
position perturbation were disabled in order to
evaluate the effects of introducing the schemes).
Table 2 summarizes the results, by showing the best
solution on each problem averaged over 50 runs and
the standard deviation values. In the table’s header,
means that , or are controlled by the
bs_fitness values; otherwise, the control is disabled
and the parameter is set to the corresponding value.
For instance, ,1.49,0, in the leftmost column,
means that the inertia weights are controlled by the
Bak-Sneppen fitness values, while the acceleration
coefficients are set to
1.49, and the
perturbation
is set to 0 (that is, no perturbation
of the particles’ positions), while ,,, in the
rightmost column, means that the algorithm uses full
control of the parameter by the Bak-Sneppen model.
Table 2: Average and standard deviation of the optimal
value for 50 trials. BS-PSO with and without acceleration
coefficients control and perturbation of the particles
positions. topology.
,., ,., ,, ,,. ,,
f
1
3.35e+01
(1.90e+02)
1.38e‐15
(3.21e‐15)
8.30e‐32
(3.47e‐31)
0.00e+00
(0.00e+00)
0.00e+00
(0.00e+00)
f
2
1.67e+05
(1.17e+06)
1.88e+02
(2.53e+02)
8.56e+01
(7.98e+01)
2.61e+01
(2.66e‐01)
2.60e+01
(1.58e‐01)
f
3
2.82e+02
(4.44e+01)
1.11e+02
(2.75e+01)
2.02e+02
(4.16e+01)
4.88e+00
(7.73e+00)
3.32e+00
(7.09e+00)
f
4
1.63e+00
(5.93e+00)
1.25e‐02
(1.26e‐02)
1.65e‐02
(2.24e‐02)
3.79e‐03
(2.29e‐03)
4.51e‐03
(4.00e‐03)
In the configuration ,,0, i.e., with only the
inertia control enabled , higher values, in general,
lead to a better performance. When the dynamic
control of is enabled (
,,0) the performance on
and
is improved, while for the other functions
the fitness value decreases when compared to the
best configuration with fixed . However, the results
are better than those attained by the suboptimal
configurations, which means that it may be an
alternative to fine-tuning the parameter. Introducing
a perturbation of the particles’ positions with the
parameter clearly improves the results, especially
when the is controlled by the model.
Table 3 summarizes the results attained by the
algorithms. TVIW-PSO and RANDIW-PSO attain
the best performance with 1.494, while
GLbestIW-PSO is better with the value given in
(Arumugam and Rao, 2006): 2.0. Comparing
suboptimal configurations of the peer-algorithms
must be avoided.
Looking at Tables 2 and 3 and comparing the
values, we conclude that BS-PSO outperforms the
other algorithms in most of the scenarios. However,
PSOs in Table 3 do not include perturbation of the
particle’s position and therefore they should be also
compared to a BS-PSO with that scheme disabled
(,,0) Table 2). Table 4 compares BS-PSO
(with and without perturbation of the particles) to
the other PSOs using Kolmogorov-Smirnov
statistical tests with 0.05 level of significance (best
configurations in Table 3 were chosen). The null
hypothesis states that the datasets from which the
offline performance and standard deviation are
calculated are drawn from the same distribution. A
‘+’ sign means that PSO 1 is statistically better than
PSO 2, ‘~’ means that the PSOs are equivalent, and
‘–’ means that PSO 1 is worse than PSO 2.
Table 3: TVIW-PSO, RANDIW-PSO and GLbestIW-
PSO. Average and standard deviation of the optimal value
for 50 trials. topology.
TVIW
.
TVIW
.
RANDIW
.
RANDIW
.
GLbestIW
.
f
1
8.64e‐29
(1.75e‐28)
2.81e‐06
(2.77e‐06)
1.22e‐18
(1.26E‐18)
6.68e+02
(2.60e+02)
2.83e+03
(1.92e+03)
f
2
1.03e+02
(9.31e+01)
5.96e+02
(1.72e+03)
7.28e+01
(6.69e+01)
2.07e+07
(1.26e+07)
3.46e+08
(9.03e+07)
f
3
7.85e+01
(2.01e+01)
5.84e+01
(1.39e+01)
1.11e+02
(2.51e+01)
1.94e+02
(2.77e+01)
1.68e+02
(2.79e+01)
f
4
8.66e‐03
(1.14e‐02)
1.22e‐02
(1.26e‐02)
1.04e‐02
(1.50e‐02)
5.96e+00
(1.62e+00)
2.34e+01
(1.53e+01)
The statistical tests demonstrate that the fully
enabled BS-PSO ,,
) outperforms the other
algorithms in every scenario, while the configuration
without a perturbation factor ,,0
) is in general
better than GLbestIW-PSO, while being competitive
with the other methods.
In the following experiment, IA-PSO was tested
with different acceleration coefficients and three
different perturbation strategies. The perturbation
factor was disabled (0, set to 0.25, as in
Table 4: Kolmogorov-Smirnov tests with 0.05 level of
significance comparing the algorithms. topology.
PSO 1 vs. PSO 2
f
1
f
2
f
3
f
4
BS-PSO ,, vs TVIW-PSO
+ + + +
BS-PSO ,, vs RANDIW-PSO
+ + + +
BS-PSO
,,
vs GLbestIW-PSO
+ + + +
BS-PSO ,,) vs TVIW-PSO
+ +
–
–
BS-PSO ,,) vs RANDIW-PSO
+ ~
–
~
BS-PSO ,,) vs GLbestIW-PSO
+ + ~ +
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
68
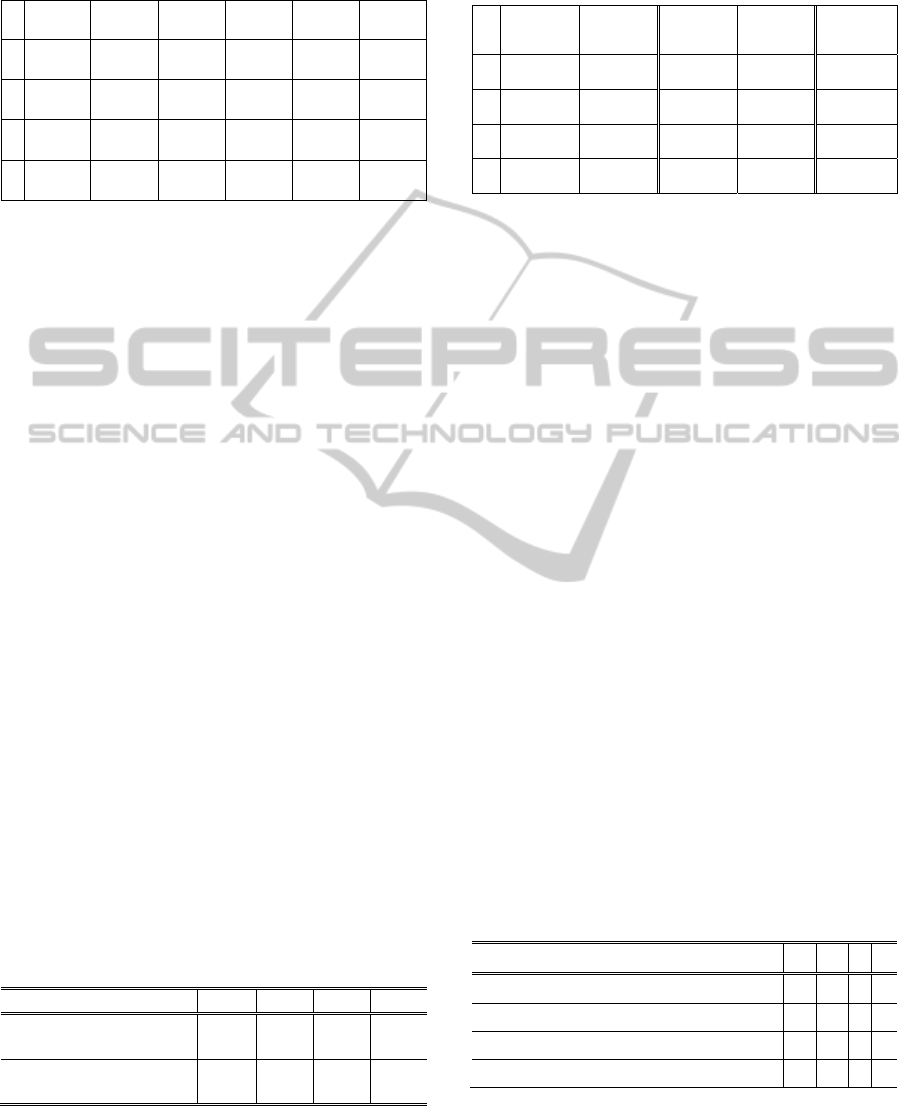
Table 5: IA-PSO. Results with different values and
perturbation strategies: no perturbation (
); controlled
by Bak-Sneppen model (
). topology.
.
.
.25
.
.
.
.25
.
f
1
2.42e+02
(1.43e+03)
0.00e+00
(0.00e+00)
0.00e+00
(0.00e+00)
5.19e‐02
(2.61e‐02)
6.56e‐03
(5.34e‐03)
2.60e‐02
(1.70e‐02)
f
2
7.45e+04
(5.26e+05)
2.62e+01
(3.71e‐01)
2.60e+01
(1.84e‐01)
4.26e+02
(8.30e+02)
3.97e+01
(2.14e+01)
7.21e+01
(8.25e+01)
f
3
2.82e+02
(3.47e+01)
5.26e+01
(3.08e+01)
3.96e+01
(2.02e+01)
8.87e+01
(2.66e+01)
1.81e+00
(3.12e+00)
1.12e+01
(1.42e+01)
f
4
2,62e+00
(1.30e+01)
3.72e‐03
(2.23e‐03)
4.71e‐03
(3.12e‐03)
1.84e+00
(1.27e+01)
1.11e‐02
(7.74e‐03)
1.30e‐02
(7.08e‐03)
(Suresh et al., 2008), and controlled by the Bak-
Sneppen model (incorporating a Bak-Sneppen
control in IA-PSO permits to compare only the
parameter control mechanism of both algorithms).
Results are in Table 5. The introduction of a
controlled by the Bak-Sneppen model seems to
improve the performance of IA-PSO. The statistical
tests in Table 6 compare BS-PSO and IA-PSO. BS-
PSO is better or at least equivalent to IA-PSO,
whether the control schemes are enabled or not.
The algorithms were also tested with topology.
The results are summarized in Table 7. BS-PSO is
better than the other algorithms in every scenario.
Moreover, statistical tests indicate that it is
significantly better than all the other algorithms in
every function, except when compared to IA-PSO
on (see Table 8). The control strategy proposed in
this paper is very efficient in this test set. When the
control schemes are fully enabled, there is a balance
between the parameter values that seems to create a
good balance between exploration and exploitation.
BS-PSO is able to outperform several algorithms,
each using a different strategy to control or set the
parameters values.
These results are not definitive but they
demonstrate the validity of the algorithm. The
following step is to understand why SOC works for
PSO. This is not a trivial task and further research is
required in order to recognize all the effects of SOC-
generated values in the behaviour of the algorithm.
Table 6: Kolmogorov-Smirnov statistical tests comparing
IA-PSO and BS-PS.
PSO 1 vs. PSO 2 f
1
f
2
f
3
f
4
BS-PSO,., vs IA-
PSO
+ + ~ +
BS-PSO
,,
vs IA-
PSO (bs controled )
~ ~ + ~
However, a simple experiment may shed some
light on the dynamics of the SOC-generated
parameters.
Table 7: Results with gbest topology.
TVIW
.
RANDIW
.
GLbestIW
.
IA-PSO
.
.25
BS-PSO
f
1
5.00e+03
(6.78e+03)
6.80e+03
(7.41e+03)
1.14e+05
(1.74e+04)
1.08e‐01
(1.17e‐01)
0.00e+00
(0.00e+00)
f
2
1.64e+02
(2.32e+02)
2.45e+02
(1.43e+03)
2.36e+08
(7.80e+07)
8.03e+02
(2.06e+03)
2.58e+01
(3.32e‐01)
f
3
6.16e+01
(1.65e+01)
1.19e+02
(2.95e+01)
4.51e+02
(7.25e+01)
5.02e+01
(4.10e+01)
4.69e+01
3.27e+01
f
4
3.62e+01
(5.77e+01)
7.05e+01
(7.80e+01)
4.21e+02
(1.40e+02)
1.36e‐01
(1.71e‐01)
1.32e‐02
(1.47e‐02)
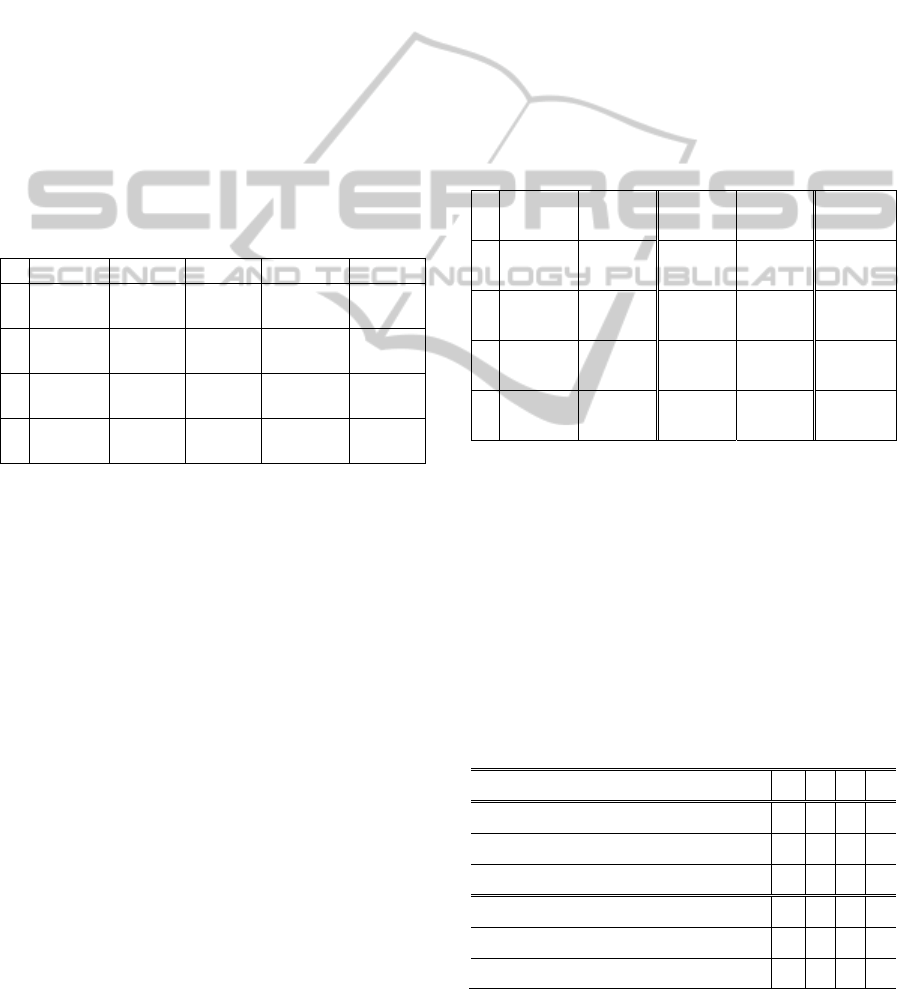
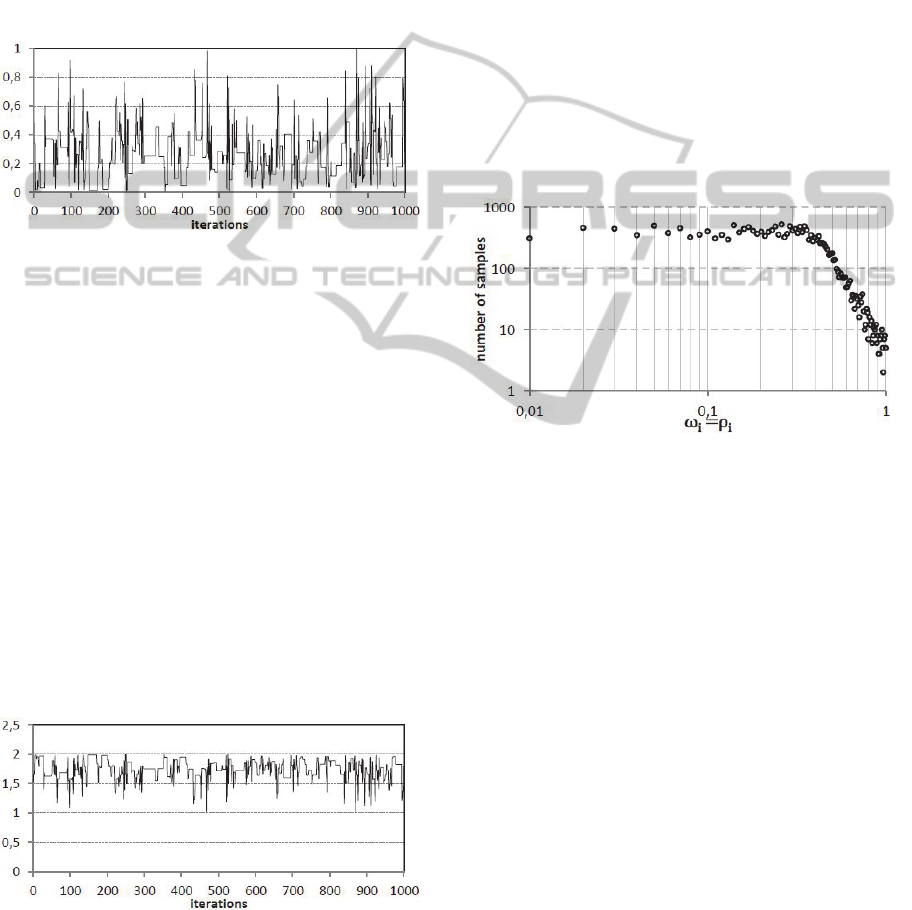
In a single run of the BS-PSO, the inertia weights
computed for one particle (particle with index 0)
in each iteration were stored and plotted in the time-
domain graphic of Figure 1. Please note that the
inertia weight is computed using the particle’s
_, with the simple formula
1
_
. Therefore, what is seen in Figure 1
is also the dynamics of the _ of particle 0.
The acceleration coefficients are plotted in Figure 2.
The inertia weight value is usually under 0.5,
with occasional peaks that go above that value. We
also see paths of stability, which demonstrate that
the of each species is not random or
chaotic. Instead, it has a hidden order that is revealed
by a different representation of the values. There are
periods of stasis, in which the parameter does not
change. The inertia weigh value during these periods
is usually between 0.2 and 0.4, which is actually the
value suggested for later stages of the search (Shi
and Eberhart, 1999). The acceleration coefficients
remain in the range 1.5,2.0 (with occasional
“bursts” that go below 1.5). The values often
suggested for these parameters are also within this
range. Such an advantageous range is of course
guaranteed by the equations 5 and 6. But the specific
dynamics of the parameter values, with periods of
stasis punctuated by strong activity, is a result of the
Bak-Sneppen model.
Table 8: Kolmogorov-Smirnov tests with 0.05 level of
significance comparing the algorithms. topology.
PSO 1 vs. PSO 2 f
1
f
2
f
3
f
4
BS-PSO ,, vs TVIW-PSO + + + +
BS-PSO ,, vs RANDIW-PSO + + + +
BS-PSO
,,
vs GLbestIW-PSO + + + +
BS-PSO ,,) vs IA-PSO + + ~ +
When plotting the distribution of all the
values computed by the model (which are also the
values) during a run an interesting pattern arises.
UsingSelf-organizedCriticalityforAdjustingtheParametersofaParticleSwarm
69
The graphic in Figure 3 divides the
values
of every particles of the swarm into the classes
defined by the intervals (
0,0.01
,…0.99,1.0 and
plots the number of samples in each class in a log-
log format. Such representation of the values permits
to determine the range of values with more activity
during a run. As seen in Figure 3, the parameter
values are uniformly spread through the range
0.01,0.3, and then the frequency decreases until it
reaches quantities two order of magnitude below the
low- and medium-range frequency.
Figure 1: Inertia weight of a particle during a typical run.
The graphic shows the typical behaviour of a
SOC system: the dynamics cover a wide range of
values, but not in a random way. Instead, some
behavioural patterns are observed. The values
oscillate usually in the low-range of the scale, with
long periods of stasis punctuated by high values.
Although they are not a definitive answer, these
results help to clarify the performance of BS-PSO.
The values are kept within a range that is not only
suited for and , but also appropriate to model a
perturbation scheme. If the system evolved higher
values with more frequency, the effect would be
destructive, since it would increase exploration
beyond a reasonable point. Please remember that
TVIW-PSO, for instance, starts with a high value
but then decreases it during the run. Furthermore,
there are periodical bursts of and that may be
helping the swarm to escape local optima traps.
Figure 2: Acceleration coefficients (
of a particle
during a typical run.
One possible limitation of the current BS-PSO is
also shown by these results, namely by the graphic
in Figure 1. The values do not depend on the state of
the search. Since the TVIW-PSO relies on a scheme
that decreases the inertia weight linearly with time,
which has been proven to be an efficient strategy, it
is possible that the proposed algorithm would gain
from modelling a similar behaviour. For that, other
levels of hybridization between the Bak-Sneppen
model and the PSO must be devised. These schemes
would incorporate information from the search into
the _ update, so that time and the fitness
distribution of the swarm could influence the
parameters’ growth. Although this can be achieved
with a deterministic strategy, letting the model and
the PSO interact and self-adjust the averaged growth
rate of the parameters keeps the method simple and
avoid the hand-tuning of extra parameters. Such
hybridization is the main target for a future research.
Figure 3: Distribution of
values of all particles in a
typical run.
6 CONCLUSIONS
This paper describes the Bak-Sneppen Particle
Swarm Optimization (BS-PSO). The algorithm uses
the Self-Organized Criticality (SOC) Bak-Sneppen
model for computing the inertia weights and the
acceleration coefficients of each particle, as well as a
perturbation factor of the particles’ positions. A
single scheme for controlling the four parameters is
used by the algorithm, which does not require hand-
tuning. Being a SOC system, The Bak-Sneppen
model is able to self-tune to a critical state and it
may be treated as a black-box that that outputs
batches of values for the parameters.
An experimental setup with four functions
demonstrates the validity of the algorithm. BS-PSO
is compared with other methods with promising
results. In particular, the algorithm is better than a
recently proposed inertia weigh PSO (IA-PSO) in
most of the experimental scenarios. The dynamics of
the parameter values, induced by the attached model,
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
70

are investigated and hypotheses that try to explain
the performance of the algorithm are put forward.
In a future work, more functions will be included
in the test set. A scalability analysis is intended as
well as a study on the effects of the limit imposed to
mutation events, and possible alternatives to the
current solution. In order to introduce information
from the search into the variation scheme of the
parameter values, different levels of hybridization
between the Bak-Sneppen model and PSO will also
be tested,. Finally, it is our intention to apply this
algorithm to time-varying fitness functions.
ACKNOWLEDGEMENTS
The first author wishes to thank FCT, Ministério da
Ciência e Tecnologia, his Research Fellowship
SFRH / BPD / 66876 / 2009, also supported by FCT
(ISR/IST plurianual funding) through the
POS_Conhecimento Program. This work is
supported by project TIN2011-28627-C04-02
awarded by the Spanish Ministry of Science and
Innovation and P08-TIC-03903 awarded by the
Andalusian Regional Government.
REFERENCES
Arumugam, M. S., Rao, M. V. C., 2006. On the
Performance of the Particle Swarm Optimization
Algorithm with Various Inertia Weight Variants for
Computing Optimal Control of a Class of Hybrid
Systems. Discrete Dynamics in Nature and Society,
vol. 2006, Article ID 79295, 17 pages.
Bak, P., Tang, C., Wiesenfeld, K., 1987. Self-organized
Criticality: an Explanation of 1/f Noise. Physical
Review of Letters, Vol. 59(4), 381-384.
Bak, P., and Sneppen, K., 1993. Punctuated Equilibrium
and Criticality in a Simple Model of Evolution.
Physical Review of Letters, Vol. 71(24), 4083-4086.
Boettcher, S., Percus, A. G., 2003. Optimization with
Extremal Dynamics. Complexity, Vol. 8(2), pp. 57-62,
2003.
Eberhart, R. C., Shi, Y., 2000. Comparing Inertia Weights
and Constriction Factors in Particle Swarm
Optimization. In Proceedings of the 2000 Congress on
Evolutionary Computation, IEEE Press, 84–88.
Eiben, A. E., Hinterding, R., Michalewicz, Z. 1999.
Parameter Control in Evolutionary Algorithms. IEEE
Trans. on Evolutionary Computation, 3(2), 124-141.
Fernandes, C. M., Merelo, J. J., Ramos, V., Rosa, A. C.
2008. A Self-Organized Criticality Mutation Operator
for Dynamic Optimization Problems. In Proceedings
of the 2008 Genetic and Evolutionary Computation
Conference, ACM, 937-944.
Fernandes, C. M., Laredo, J. L. J., Mora, A. M., Rosa, A.
C., Merelo, J. J., 2011. A Study on the Mutation Rates
of a Genetic Algorithm Interacting with a Sandpile. In
Proc. of the 2011 International Conference on
Applications of Evolutionary Computation I, C. Di
Chio et al. (Eds.), Springer-Verlag,, 32-42.
Grefenstette, J. J., 1992. Genetic Algorithms for Changing
Environments. In Proceedings of Parallel Problem
Solving from Nature II, North-Holland, Amsterdam,
137-144.
Kennedy, J., Eberhart, R., 1995. Particle Swarm
Optimization. In Proceedings of IEEE International
Conference on Neural Networks, Vol.4, 1942–1948.
Kennedy, J., Eberhart., R. C., 2001. Swarm Intelligence.
Morgan Kaufmann, San Francisco.
Krink, T., Rickers, P., René, T., 2000. Applying Self-
organized Criticality to Evolutionary Algorithms. In
Proceedings of the 6
th
International Conference on
Parallel Problem Solving from Nature (PPSN-VI),
LNCS 1917, Springer, 375-384.
Krink, T., Thomsen, R., 2001. Self-Organized Criticality
and Mass Extinction in Evolutionary Algorithms. In
Proceedings of the 2001 IEEE Congress on
Evolutionary Computation (CEC’2001), Vol. 2, IEEE
Press, 1155-1161.
Løvbjerg, M., Krink, T., 2002. Extending particle swarm
optimizers with self-organized criticality. In
Proceedings of the 2002 IEEE Congress on
Evolutionary Computation, Vol. 2, IEEE Computer
Society, 1588–1593.
Ratnaweera, A., Halgamuge, K. S., and Watson, H. C.,
2004. Self-organizing Hierarchical Particle Swarm
Optimizer with Time-varying Acceleration
Coefficients. IEEE Transactions on Evolutionary
Computation, Vol. 8(3), 240-254.
Shi, Y. Eberhart, R. C., 1998. A Modified Particle Swarm
Optimizer. In Proceedings of IEEE 1998 International
Conference on Evolutionary Computation, IEEE
Press, 69–73.
Shi, Y. Eberhart, R. C., 1999. Empirical Study of Particle
Swarm Optimization. In Proceedings of the 1999
IEEE Int. Congr. Evolutionary Computation, vol. 3,
1999, 101–106.
Suresh, K., Ghosh, S., Kundu, D., Sen, A., Das, S.,
Abraham, A., 2008. Inertia-Adaptive Particle Swarm
Optimizer for Improved Global Search. In
Proceedings of the 8
th
Inter. Conference on Intelligent
Systems Design and Applications, Vol. 2. IEEE,
Washington, DC, USA, 253-258.
Tinós, R., Yang, S., 2007. A self-organizing Random
Immigrants Genetic Algorithm for Dynamic
Optimization Problems. Genetic Programming and
Evolvable Machines, Vol. 8(3), 255-286.
UsingSelf-organizedCriticalityforAdjustingtheParametersofaParticleSwarm
71
