MR Damper Identification using ANN based on 1-Sensor
A Tool for Semiactive Suspension Control Compliance
Juan C. Tud´on-Mart´ınez, Ruben Morales-Menendez, Ricardo A. Ramirez-Mendoza
and Luis E. Garza-Casta˜n´on
Tecnol´ogico de Monterrey, Av. E. Garza Sada 2501, 64849, Monterrey N.L., Mexico
Keywords:
Magneto-Rheological Damper, Artificial Neural Networks, Semiactive Suspension Control.
Abstract:
A model for a Magneto-Rheological (MR) damper based on Artifical Neural Networks (ANN) is proposed.
The ANN model does not require regressors in the input and output vector, i.e. is considered static. Only one
sensor is used to achieve a reliable MR damper model which is compared with experimental data provided
from two MR dampers with different properties. The RMS of the error is used to measure the model accuracy;
from both MR dampers, an average value of 7.1% of total error in the force signal is obtained by taking into
account 5 different experiments. The ANN model, which represents the nonlinear behavior of an MR damper,
is used in a suspension control system of a Quarter of Vehicle (QoV) in order to evaluate the comfort of
passengers maintaining the road holding. A control technique with the MR damper model is compared with
a passive suspension system. Simulation results show the effectiveness of a semiactive suspension versus the
passive one. The RMS of the comfort signal improves 7.4% with the MR damper while the road holding gain
in the frequency response shows that the safety in the vehicle can be increased until 40.4% with the semiactive
suspension system. The accurate MR damper model validates a realistic QoV response compliance.
1 INTRODUCTION
A Magneto-Rheological (MR) damper is an hydraulic
damper whose oil contains metallic particles that
change the rheological properties (i.e. viscosity) of
the fluid when a magnetic field is applied; an electric
current supplied through the damper coil is used to
manipulate the magnetic phenomenon. The variation
of the oil viscosity allows to modify the damping ra-
tio in the shock absorber, this property is named semi-
activity. The oil viscosity is proportional to the elec-
tric current as well as to the MR damper force; how-
ever, the join of these mechanisms creates an highly
nonlinear behavior in the damping force. The MR
damper has been mainly applied in vibration control
because it has low power requirement, fast response,
simple structure and continuous adjustable damping
force over a large span.
The main function of the MR damper in an auto-
motive suspension is to absorb energy in order to get
low accelerations of the sprung mass (i.e. automo-
tive chassis) and low deflections in the wheel; thus,
an accurate MR damper model is required to design
the control system. Even there are important contri-
butions in this field (Guo et al., 2006); there are still
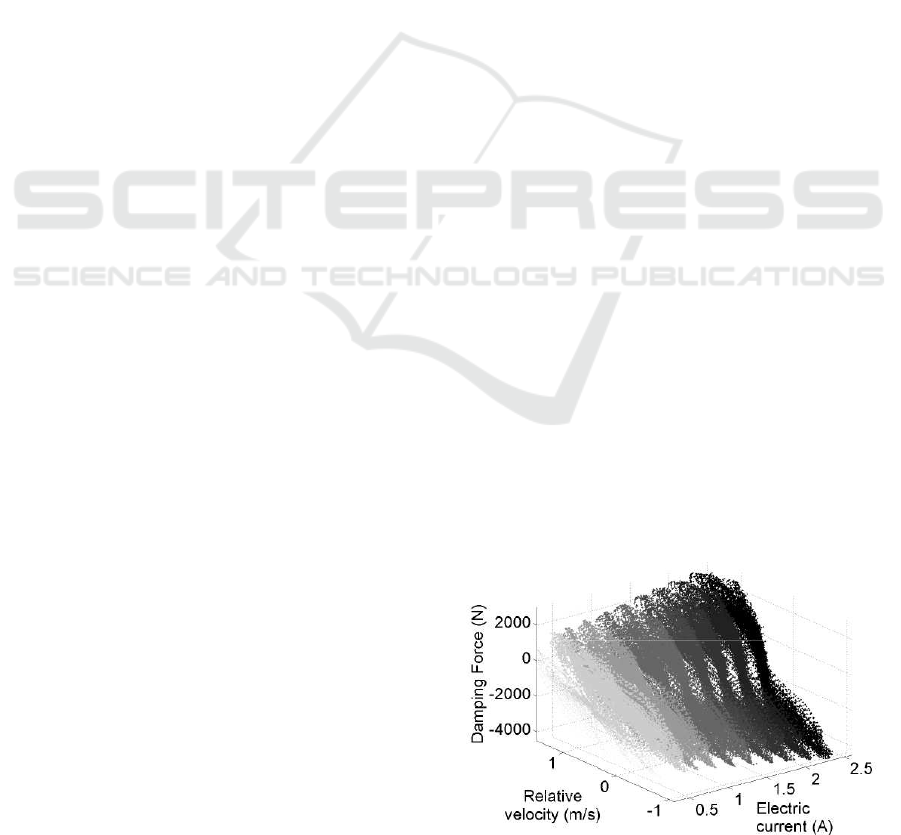
several needs. Figure 1 shows the highly nonlinear
behavior of an industrial MR damper under various
constant electric current inputs, its accurate modeling
is a non-trivial task.
Figure 1: Nonlinear behavior of the MR damper force re-
spect to the control current and relative velocity.
Several mathematical models are available for
modeling the nonlinear behavior of MR dampers;
generally, they can be grouped as parametric and
non-parametric models. Parametric models in-
clude the Bingham model (Stanway et al., 1987),
493
C. Tudón-Martínez J., Morales-Menendez R., A. Ramirez-Mendoza R. and E. Garza-Castañón L..
MR Damper Identification using ANN based on 1-Sensor - A Tool for Semiactive Suspension Control Compliance.
DOI: 10.5220/0004159004930502
In Proceedings of the 4th International Joint Conference on Computational Intelligence (NCTA-2012), pages 493-502
ISBN: 978-989-8565-33-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

the viscoelastic-plastic model (Gamota and Filisko,
1991), the phenomenological model (Wang and
Kamath, 2006), the semi-phenomenological model
based on the BoucWen model (Spencer et al., 1996),
the improved BoucWen model (Yang et al., 2002),
the hyperbolic tangent function model (Kwok et al.,
2006), (Guo et al., 2006), the inverse tangent func-
tion model (C¸ esmeci and Engin, 2010) and many oth-
ers. The Bingham and the viscoelastic-plastic model
can not reproduce the nonlinear behavior of an MR
damper with high accuracy, while the other models
can; however, they have many parameters to identify.
On the other hand, some of these physical models use
parameters of the internal structure of the shock ab-
sorber resulting a particular model case.
In the non-parametric models, the coefficients do
not have a physical meaning. Models based on look-
up table, fuzzy logic and Artificial Neural Networks
(ANN) are the representative non-parametric models
for a MR damper. Polynomial models [(Choi et al.,
2001), (Hong et al., 2002), (Du et al., 2005), (Poussot-
Vassal et al., 2008)] require many parameters to ex-
press the nonlinear and semiactive behavior of the
damping force; while the fuzzy models [(Atray and
Roschke, 2003), (Ahn et al., 2008)] need a priori
knowledge in the frequency and time domain of the
MR damper. For ANN models, the knowledge of the
dynamic relationships between the variables is not re-
quired, only a well training step is needed; in addi-
tion, the number of parameters depends on the struc-
ture size and commonly the ANN design is based on
the minimal dimensions criterion (Freeman and Ska-
pura, 1991), which selects the possible lowest number
of hidden layers with the possible lowest number of
neurons.
The major effort in the MR damper modeling, by
using ANN, is focused on reproduce the inverse dy-
namics (force-electric current) of the shock absorber
(Chang and Zhou, 2002), (Zapateiro et al., 2009),
(Metered et al., 2010); however, a recurrent neural
network is required for achieving an optimal damping
force signal, and normally the input vector is based on
two or more sensor measurements: force, displace-
ment and/or velocity. This type of ANN model in-
creases the architecture size and the instrumentation
cost in a suspension control system. On the other
hand, commonly the modeling of the forward dynam-
ics using ANN requires two ore more time delays of
each input by increasing the ANN architecture and its
computing time (Savaresi et al., 2005), (Chen et al.,
2009), (Boada et al., 2011).
This paper proposes a non-parametricmodel of an
MR damper based on ANN, the model does not require
regressors in the input vector and demands only one
sensor, i.e. its structure has low complexity for prac-
tical implementations of suspension control systems.
The MR damper model is validated with experimen-
tal data of two MR dampers for analyzing its reliabil-
ity and it is used in a suspension control system of a
Quarter of Vehicle (QoV), this is an example of an ap-
plication problem where the accurate modeling of the
actuation device is one of the most crucial part of the
whole control design problem.
The outline of this paper is as follows: in the next
section, the ANN design is described. Section 3 shows
the experimental system and section 4 presents the
modeling results. Section 5 presents the effectiveness
of an MR damper versus a passive damper in compli-
ance of a suspension control system. Conclusions are
presented in section 6.
Table 1: Definition of variables.
Variable Description
F
MR
MR damper force
z
de f
Damper piston position
˙z
de f
Damper piston velocity
I Electric current
k
i
Time delays
m
s
Sprung mass in the QoV
m
us
Unsprung mass in the QoV
z
r
Road profile
z
s
Vertical position of m
s
z
us
Vertical position of m
us
˙z
s
Vertical velocity of m
s
˙z
us
Vertical velocity of m
us
¨z
s
Vertical acceleration of m
s
¨z
us
Vertical acceleration of m
us
k
s
Spring stiffness coefficient
k
t
Wheel stiffness coefficient
2 ANN REVIEW
An ANN is a computational model capable to learn
behavior patterns of a process, it can be used to model
nonlinear, complex and unknown dynamic systems,
(Korbicz et al., 2004). Based on the flow of signals,
the ANN architecture can be classified into two major
groups: feedforward and recurrent networks. Feed-
forward networks project the flow of information only
in one way, i.e. the output of a neuron feeds to all
neurons of the following layer (Hagan et al., 1996);
while, the recurrent networks have an output feedback
signal.
In MR damper modeling using ANN, typically
recurrent neural networks based on Nonlinear-ARX
(NARX) structures, i.e. regressors in the input and/or
output vector, have been proposed with high accuracy
(Chang and Zhou, 2002), (Savaresiet al., 2005), (Zap-
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
494

ateiro et al., 2009), (Chen et al., 2009), (Metered et al.,
2010), (Boada et al., 2011). The NARX structure is
defined as,
F
MR
= f
NL
(z
de f
(t), z
de f
(t − 1), . . . , z
de f
(t −k
1
),
˙z
de f
(t), ˙z
de f
(t −1), . . . , ˙z
de f
(t −k
2
),
I(t), I(t − 1), . . . , I(t − k
3
),
F
MR
(t − 1), . . . , F
MR
(t −k
4
))
(1)
where k
i
represents a specific number of time de-
lays for each signal, z
def
and ˙z
def
are the displacement
and velocity of the damper rod provided from sensor
measurements, I is the actuation signal and F
MR
is the
damper force (ANN output).
In this paper, a comparison between a feedforward
and recurrent neural network is considered for deter-
mining the accuracy degree in the damper force by
adding the output feedback in the ANN structure. In
addition, different arrays in the input vector are used
to evaluate the ANN performance with time delays;
the arrays with one, two and three regressors in the
input vector are compared with the modeling perfor-
mance of an ANN that does not have delays. Finally,
the ANN performance is analyzed when one (velocity)
or two (displacement and velocity) signals are used in
the input vector.
The ANN training is defined as the adaptation pro-
cess of the synaptic connections under external stim-
ulations. The backpropagation algorithm is the most
used training method since it allows to solve prob-
lems with complex net connections; its formulation
can be reviewed in detail in (Freeman and Skapura,
1991). The proposed ANN model was trained with
backpropagation and crossed validation was used to
validate the results.
3 EXPERIMENTAL SYSTEM
Two different MR dampers have been used to perform
a total of 5 tests. One damper, called MR
1
damper,
is designed by Delphi MagneRide
TM
; it has continu-
ous actuation and considerable hysteresis at high fre-
quencies with high deflections. The other MR damper,
named MR
2
damper, is manufactured by BWI
TM
; it
has only two levels of actuation and its hysteretic be-
havior is minimal.
An MTS-407
TM
controller has been used to con-
trol the position of the damper piston, Figure 2. An
NI-9172
TM
data acquisition system commands the
controller and records the position, velocity and force
from the MR damper. A sampling frequency of 1650
Hz was used. The bandwidth of displacement was
0.5- 15 Hz, which lies within comfort and road hold-
ing automotive applications. The displacement and
electric current ranges were: ±25 mm and 0 - 2.5 A,
respectively.
Figure 2 also shows the used sensor (VP510-10
of UniMeasure
TM
), which provides the velocity (˙z
def
)
and position (z
def
) measurements of the damper pis-
ton. In this case, a self-generating tachometer gener-
ates the velocity measurement; however, it is possible
to use another linear velocity transducer.
MTS System
Position and
velocity sensor
MR damper
Figure 2: Experimental system.
A series of training sequences have been proposed
in (Lozoya-Santos et al., 2009), the position emulates
the suspension deflection and the electric current is
the actuation signal. Table 2 shows the design of ex-
periments used to identify the nonlinear behavior of
both MR dampers under different sequences of posi-
tion and actuation.
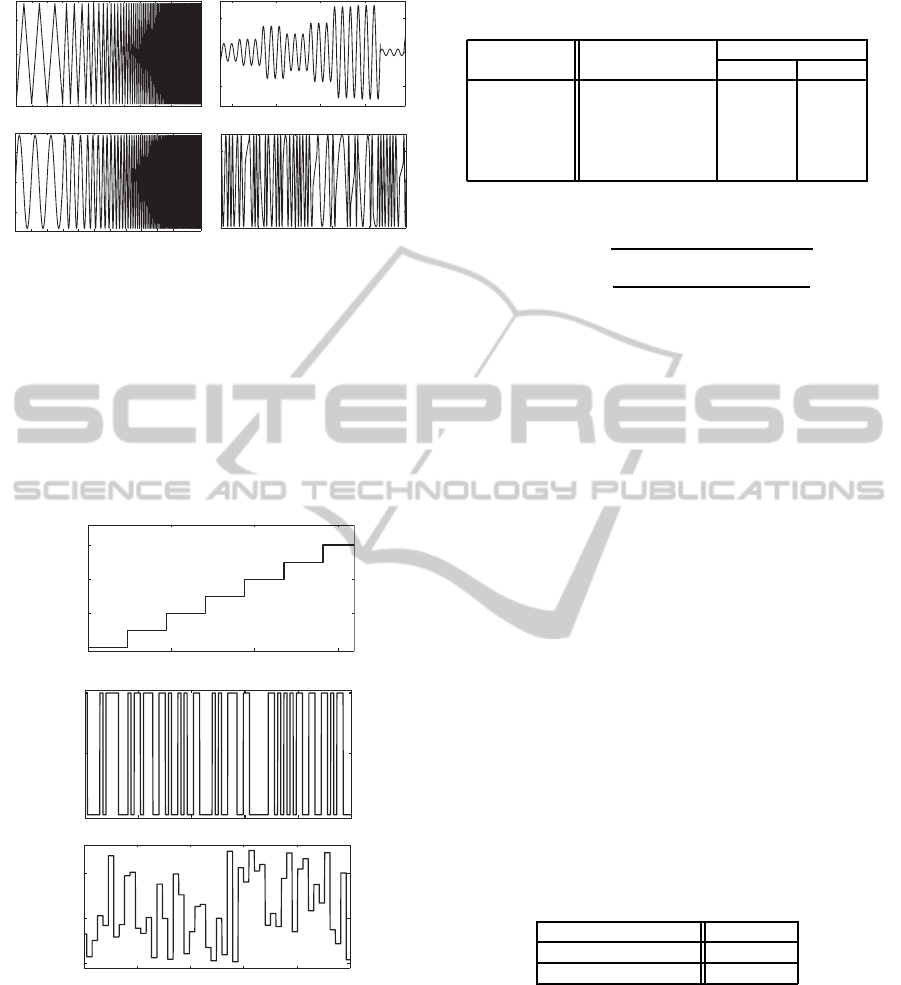
For displacement sequences, Amplitude-
Modulated (AM), Frequency-Modulated (FM)
and Stepped Frequency Sinusoidal (SFS) were used
to analyze the MR damper dynamics in the transient
response under changes in magnitude and frequency
of the suspension deflection; Triangular wave with
Positive and Negative Variable Slopes (TPNVS)
sequence allows to know the dynamic behavior under
constant velocity; and Road Profile (RP) represents
the suspension deflection move when the vehicle
passes under a specific surface. Figure 3 presents
some of the different displacement sequences used
in the experimental stage in order to identify the
nonlinear behavior of both MR dampers.
For electric current sequences, Stepped inCre-
ments (SC) are used to study the effect of the current
in the jounce and rebound of the MR damper under
different displacements, since the MR
2
damper has
not a continuous actuation only two levels of current
were designed; Increased Clock Period Signal (ICPS)
and Pseudo Random Binary Signal (PRBS) allow to
analyze the transient response of the damping force
MRDamperIdentificationusingANNbasedon1-Sensor-AToolforSemiactiveSuspensionControlCompliance
495
2 4 6 8 10 12 14 16 18 20
-20
0
20
Displacement (mm)
2 10 20
0
-20
20
Displacement (mm)
36 40 44 48
-20
0
20
TPNVS
SFS
AM
11 12 13 14 15
-20
0
20
FM
Time (s)
Figure 3: Displacement sequences in the piston used in the
experimental stage.
when the current changes at different frequencies, the
ICPS signal includes random changes in the ampli-
tude and PRBS only switches between two electric
current values. Figure 4 shows the behavior of the
actuation sequences used in the experiments, for the
MR
2
damper, the SC sequence only has two states: 0
and 2.5 A.
0 50 100 150
0.6
1.2
2.5
Electric Current (A)
SC
11 12 13 14
0
1
2
Electric Current (A)
ICPS
6 7 8 9
0
2.5
PRBS
Time (s)
Electric Current (A)
Figure 4: Electric current sequences used in the experimen-
tal stage.
4 MODELING RESULTS
The ANN model obtained from the different experi-
ments, presented in Table 2, is used to characterize
the dynamical behavior of the MR damper and eval-
uated by the Root Mean Square (RMS) performance
Table 2: Design of experiments for identifying an MR
damper.
Experiment Displacement Current sequence
sequence MR
1
MR
2
1 TPNVS SC (10) SC (2)
2 SFS SC (10) SC (2)
3 RP (rough way) ICPS PRBS
4 AM ICPS PRBS
5 FM ICPS PRBS
index of the error, which is defined as,
RMS =
s
∑
n
i=1
ˆ
F
MR
(i) − F
MR
(i)
2
n
(2)
where,
ˆ
F
MR
and F
MR
represent the estimated and ex-
perimental damping force respectively and n is the
number of total samples in the experiment. The per-
centage of error represents the RMS of the error nor-
malized by the span of the damping force.
First, the design issues for the ANN model are dis-
cussed: the network structure, the required sensors in
the input vector, the regressor choice and the selection
of the number of parameters of the ANN.
Remark: ANN architecture. A Multilayer Percep-
tron (MLP) network, which corresponds to a feedfor-
ward system, is compared with a recurrent network.
The input vector of the MLP network is composed
by z
def
, ˙z
def
, I; while the recurrent network adds the
ANN output (damping force). Table 3 presents the
modeling error of both structures by using the exper-
iment 2 in the MR
1
damper as example. The error
percentage represents the average deviation between
the modeled damping force and the real measurement
based on the RMS value of the error. When the feed-
back of the MR damper force is considered, the mod-
eling error decreases slightly; however, the ANN ar-
chitecture and its computing time increase.
Table 3: Performance comparison between the feedforward
and recurrent neural networks.
ANN Structure Error (%)
MLP (feedforward) 4.38
Recurrent 3.80
Remark: Sensors in the Input Vector. Taking into
account an MLP network, two different input vectors
have been compared. The former input vector uses
the z
def
, ˙z
def
and I; while the second one only in-
cludes ˙z
def
and I. Table 4 indicates that the model-
ing error decreases 46.7 % by considering two sensor
measurements in addition to the electric current sig-
nal; however, the instrumentation cost can increase
and the ANN structure is more complex for the train-
ing and testing step.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
496
Table 4: Modeling error (%) in the MLP network using dif-
ferent input vectors.
Sensor Measurements Error (%)
1 (˙z
de f
) 8.22
2 (z
de f
and ˙z
de f
) 4.38
Remark: Regressor Choice. Once the ANN archi-
tecture and the input vector are defined, different ar-
rays in the input vector of the ANN model have been
evaluated, in this case the experiment 2 over the MR
1
damper is used as example. Table 5 shows the model-
ing error of the ANN when the number of regressors
in the 2 input signals varies; in this analysis, the ve-
locity and electric current have the same number of
regressors in each test. According to the modeling er-
ror, it is not significant to incorporate time delays in
the input vector of the ANN.
Table 5: Modeling error (%) in the ANN with different num-
ber of regressors in the input vector.
Regressors Error (%)
0 8.22
1 8.24
2 8.86
3 8.79
Remark: ANN-size Selection. Finally, the choice of
the number of parameters (hidden layers and neurons
in these layers) of the non-linear parametric function
can be easily made using a cross-validation approach.
A 1-hidden-layer structure has been chosen by sim-
ulation tests, this structure guarantees the universal-
approximation property (Sj¨oberg, 1995). For deter-
mining the number of neurons in the hidden layer, the
minimal dimensions criterion is used (Freeman and
Skapura, 1991); the best choice is with 10 neurons.
According to the above design issues, the ANN ar-
chitecture used to model the MR damper dynamics is
(2,10,1), Figure 5. The ANN input vector includes the
signal of the relative velocity and the excitation sig-
nal (electric current) without considering regressors,
while the damping force corresponds to the ANN out-
put. Modeling results of the proposed ANN model,
considering the 5 experiments, is shown in the Table
6. Figure 6 shows the variability of the modeling re-
sults. Clearly, the variance of the error is greater in the
model of the MR
1
damper since its continuous actu-
ation adds more nonlinearities, which complicate the
modeling task; while, the MR
2
damper model shows
better modeling performance with lower error stan-
dard deviation of the error.
The RMS average, considering all experiments, is
291.4 N for the MR
1
damper and 597.8 N for the
MR
2
damper. Since the span of the force is ±4000
F
o
r
c
e
D
a
m
p
i
n
g
Displacement or
velocity sensor
Electric
Curre
nt
Input
layer
Output
layer
Hidden layer
Figure 5: Feedforward ANN of the MR damper model.
Table 6: Modeling error in different experimental tests.
MR Experiment
damper 1 2 3 4 5
MR
1
5.9% 8.2% 3.1% 4.1% 14.95%
MR
2
6.9% 6.8% 7.2% 8.0% 6.2%
2
4
6
8
10
12
14
MR
Percentage of error
MR
1 2
Figure 6: Variability of the error in the MR damper models.
N approximately for the MR
1
damper and [−6000 to
11000] N for the MR
2
damper, the obtained RMS av-
erage represents the 7.25% and 7.02% of punctual er-
ror in the force signal, respectively. Figure 7 presents
a qualitative comparison in the transient response of
the force obtained from experimental data and from
ANN model; in this case, the MR
1
and MR
2
dampers
are subject to the experiment 5. According to Table
6, the MR
1
damper has greater modeling error in the
experiment 2 and 5, and viceversa.
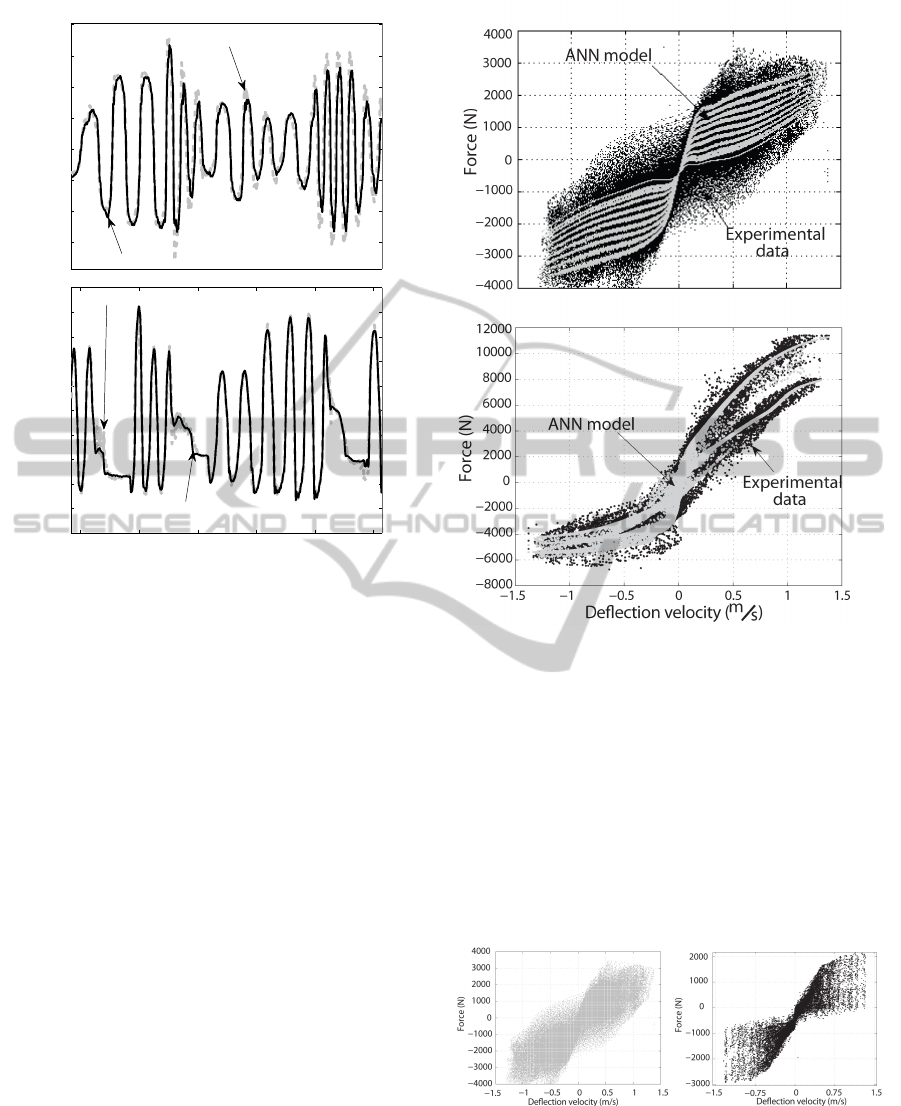
In order to test the capability of the ANN for
modeling the nonlinear and hysteretic behavior of the
MR damper, experimental data are compared with the
ANN model in the characteristic diagram of Force-
Velocity (FV); this diagram explains the effect of
jounce and rebound of the damper and it is a tool for
the engineers of automotive design in order to define
the suspension capability for improving the confort
and road holding. Figure 8 shows the FV diagram of
MRDamperIdentificationusingANNbasedon1-Sensor-AToolforSemiactiveSuspensionControlCompliance
497
0.95 1 1.05 1.1 1.15 1.2
x 10
4
−8000
−6000
−4000
−2000
0
2000
4000
6000
8000
10000
12000
Samples
Force (N)
ANN model
Experimental data
−3000
−2000
−1000
0
1000
2000
3000
4000
Force ( N)
Experimental data
ANN model
Figure 7: Comparison between the real and modeled force
using the MR
1
damper (up) and MR
2
damper (bottom).
both dampers using the experiment 2. Bottom plot
in Figure 8 shows that the ANN can model the non-
linear behavior of the MR
2
damper with acceptable
accuracy, only outliers are not included. Notice in the
FV diagram that the MR
2
damper has minimal hys-
teresis and it is composed by two damping leves: 1)
high damping force at current greater than 2.5 A and
2) low damping force at 0 A. On the other hand, the
MR
1
damper has a continuous actuation between 0
and 2.5 A. The ANN correctly models the nonlinear
behavior at each current step; however, the hystere-
sis can not be modeled at low deflection velocities
(±0.5 m/s) using only one sensor, up plot in Figure
8. This hysteretic behavior occurs at high frequencies
(greater than 10 Hz) with high amplitudes in the sus-
pension deflection, and the velocity sensor does not
contain the required information for representing the
force dynamics at these frequencies; thus, an accel-
eration sensor could complement this missing force
dynamics.
Although the hysteresis can not be modeled at
high frequencies with high displacements, in general,
the proposed ANN can be used to represent the MR
damper dynamics since the hysteretic behavior ap-
pears at not typical deflection amplitudes in an auto-
motive suspension and the frequencies out of the de-
sired span for passengers comfort, i.e. the position
Figure 8: FV diagram for the real and modeled force using
the MR
1
damper (up) and MR
2
damper (bottom).
pattern is out of the automotive operational zone of
the damper. Figure 9 shows the comparison of the
FV diagram using experimental data provided from
the experiment 2 (left plot) and 4 (right plot). Since
the experiment 4 contains data at high frequencies but
low amplitudes on the displacement, the hysteresis
phenomenon is minimal; while, the experiment 2 has
high displacements at high frequencies that cause too
much hysteresis.
Figure 9: FV diagram for the MR
1
damper using experi-
mental data from experiment 2 (left) and 4 (right).
Another form of getting the ANN model of the MR
damper is by using the estimated deflection velocity
through a displacement sensor. Figure 10 shows that
the measurement of the deflection velocity is prac-
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
498
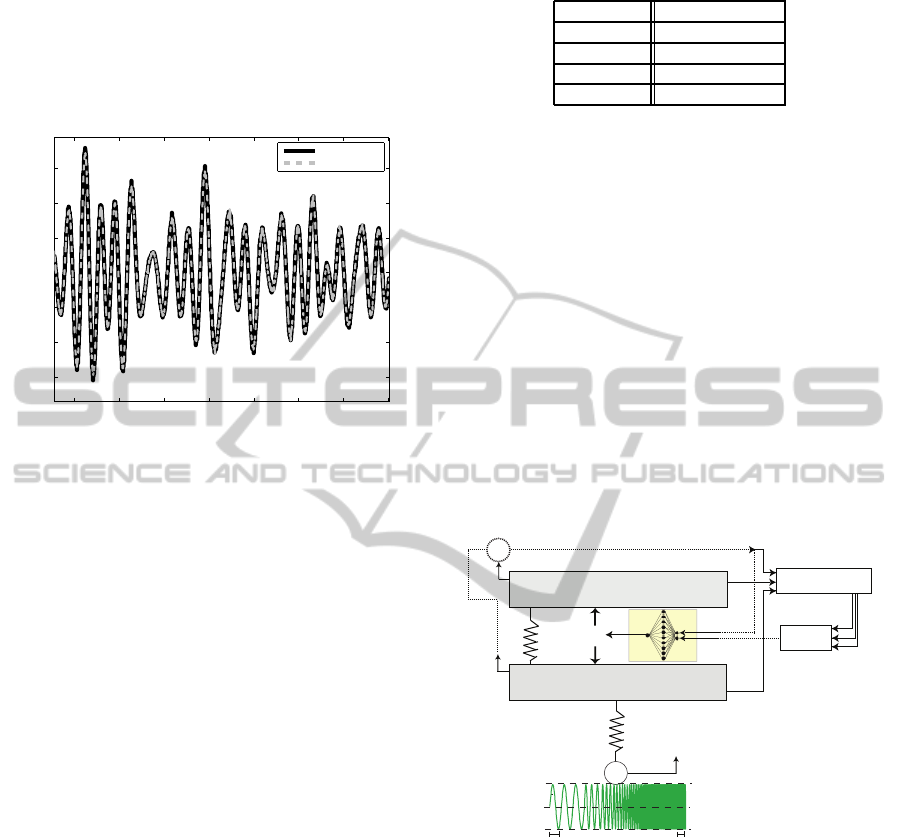
tically similar to the estimated signal, in this case
the central differentiation algorithm over the displace-
ment measurement is considered. Therefore, it can
be used a displacement or velocity sensor, additional
to the actuation signal, for achieving a reliable MR
damper model based on ANN.
1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9
x 10
4
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
Samples
Deection velocity [m/s]
Measurement
Estimation
Figure 10: Comparison between the real and estimated de-
flection velocity for the experiment 3 in the MR
2
damper.
5 MR DAMPER USED IN
AUTOMOTIVE SUSPENSIONS
In order to analyze the effectiveness of the MR
damper model based on ANN, a semiactive suspen-
sion control system of a QoV model is used as test-
bed; the ANN model is included for increasing the
comfort of passengers maintaining the road holding.
The QoV model considers a sprung mass (m
s
) and
an unsprung mass (m
us
). A spring with stiffness co-
efficient k
s
and a MR damper represent the suspen-
sion between both masses. The stiffness coefficient k
t
models the wheel tire. The vertical position of the
mass m
s
(m
us
) is defined by z
s
(z
us
), while z
r
cor-
responds to the road profile. It is assumed that the
wheel-road contact is ensured.
The system dynamics is given by,
m
s
¨z
s
= −k
s
(z
s
− z
us
) − F
MR
(3)
m
us
¨z
us
= k
s
(z
s
− z
us
) − k
t
(z
us
− z
r
) + F
MR
(4)
where, F
MR
is the MR damping force obtained by the
ANN model, which is based on the MR
2
damper dy-
namics. The QoV model parameters described in 3
and 4 have been identified on a commercial vehicle,
Table 7.
The MR force depends on the deflection velocity
˙z
def
= ˙z
s
− ˙z
us
and electric current I, this later signal
represents the controller output. Several approaches
Table 7: QoV model parameters of a commercial vehicle.
Parameter Value
m
s
387 (Kg)
m
us
139.5 (Kg)
k
s
37,300 (N/m)
k
t
295,200 (N/m)
in control of semiactive suspensions have been pro-
posed (Dong et al., 2010), (Spelta et al., 2010), etc.
The comfort performance of a semiactive sus-
pension, using the Mix 1-sensor (Mix1) control law,
is compared with a commercial vehicle suspension
which uses a passive damper. Experimental data
of the passive damper were modeled by the same
ANN technique as the semiactive dampers. Figure 11
shows a conceptual diagram of the semiactive suspen-
sion control system; the ANN model, which has been
trained off-line, only requires the deflection velocity
and the electric current for generating the MR force in
a forward way. The block of processing of signals in-
cludes filters, estimators and/or observers in order to
achieve the control law. Details on the Mix1 control
law can be reviewed in (Spelta et al., 2010).
m
m
z
z
z
k
t
r
us
s
s
us
z
def
+
-
I
k
0
peak
-
(mm)
s
z
r
z
us
. .
z
s
. .
F
MR
z
r
peak
z
r
Processing of signals
.
.
.
Controller
0.5 Hz
20 Hz
Figure 11: General structure of semiactive suspension con-
trol system.
In order to analyze the passengers comfort and
road holding in the frequency and time domain, two
road disturbance inputs have been simulated: 1) in the
frequency domain, a signal chirp of 2 cm with span
of [0.5-20]Hz and 2) in the time domain, a step of 3
cm. Figure 12 shows the QoV performance in the fre-
quency domain; the Power Spectral Density (PSD) is
used as performance index, i.e. the maximum gain of
a signal is plotted at any specific frequency. The fre-
quency response of the QoV model with the passive
damper is considered as benchmark.
According to (Poussot-Vassal et al., 2008), Fig-
ure 12 shows that the controller fulfills with the per-
MRDamperIdentificationusingANNbasedon1-Sensor-AToolforSemiactiveSuspensionControlCompliance
499
2 4 6 8 10 12 14 16 18 20
50
100
150
200
250
300
350
gain
2 4 6 8 10 12 14 16 18 20
0.5
1
1.5
2
2.5
3
3.5
4
frequency [Hz]
gain
Mix-1
passive
Comfort z
s
..
Road Holding z - z
us r
Mix-1
passive
Figure 12: Frequency response of the QoV model in closed-
loop using a semiactive and passive suspension, the span of
frequencies of interest for each objective is bounded by the
vertical discontinuous lines.
formance specification for comfort: at low frequen-
cies [0-2]Hz, the maximum gain of ¨z
s
respect to the
surface is lower than the passive suspension. In this
range of frequencies, a human can feel dizziness and
sickness caused by sudden motions. On the other
hand, a good road holding is considered when the
maximum gain of z
us
− zr respect to z
r
is limited to
2.5 for low disturbances (z
r
< 3cm) between 0 to 20
Hz, specially close to the resonance frequency of m
us
.
Bottom plot in Figure 12 indicates that the semiac-
tive suspension control system has good road hold-
ing performance in all span of frequencies, the PSD
reduces until 2 units in the resonance frequency of
the unsprung mass. Thus, the road holding increases
40.4% by using a semiactive suspension system.
For the time domain, the effectiveness of the semi-
active suspension versus the passive suspension is
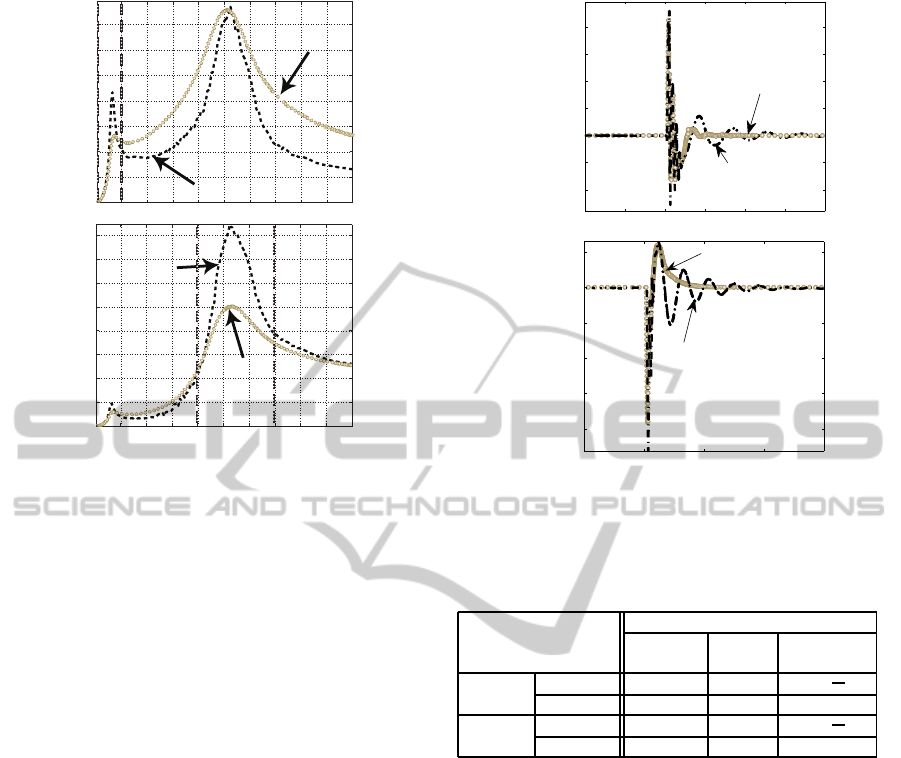
clear. Figure 13 displays the transient response of
the acceleration of the sprung mass (up plot) and of
the wheel deflection (bottom plot). In both transient
responses, the semiactive control system can reduce
more of 50% in the settling time and decay ratio and
approximately a 10% of the the maximum deviation,
Table 8. Taking into account the RMS of the ¨z
s
signal,
the comfort increases 7.4% with the Mix1 controller.
For road holding, the Mix1 controller improves 64.9%
respect to he passive suspension.
500 1000 1500 2000 2500 3000
−2
−1
0
1
2
3
4
1000 2000 3000 4000
−0.04
−0.03
−0.02
−0.01
0
0.01
Samples
Passive
Mix 1
Mix 1
Passive
Comfort z
s
..
Road Holding z - z
us r
(m)
(m/s )
2
Figure 13: Transient response of the QoV model in closed-
loop using different automotive suspension schemes.
Table 8: Performance in the transient response of the sus-
pension control system.
Suspension Performance Index
Control Settling Decay Maximum
System Time (s) Ratio Deviation
Semi- Comfort 0.3 0.07 4.1
m
s
2
active Holding 0.6 0 -3.8cm
Passive Comfort 0.8 0.15 4.5
m
s
2
Holding 1.7 0.23 -4.5cm
6 CONCLUSIONS
A Magneto-Rheological (MR) damper model based
on Artificial Neural Networks (ANN) is proposed.
The ANN structure does not require regressors in the
input vector and only one sensor (displacement or ve-
locity) is demanded to get a reliable model. In addi-
tion, it has been proved that the output feedback in the
input vector of the ANN model only improves slightly
the modeling performance; however, the computing
time in the training and testing step increases because
the ANN architecture requires more model parameters
when the output feedback is included.
Experimental data provided from two MR
dampers (Delphi
TM
named MR
1
damper, and BWI
TM
named MR
2
damper) with different properties have
been used to verify the accuracy of the proposed MR
damper model based on ANN. The average modeling
error in the force signal is lower than 7.25% by con-
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
500

sidering 5 different experiments. The force-velocity
diagram shows that the MR
2
damper can be mod-
eled with high accuracy by the proposed ANN struc-
ture since this shock absorber has an on/off actuation
and does not have hysteresis; while the MR
1
damper
presents a more complex dynamics at high frequen-
cies with high displacements and the MR damper
model based on the proposed 1-hidden layer structure
can not represent this hysteretic behavior with only
one sensor. However, this displacement pattern is out
of the automotive operational zone of the damper, i.e.
it does not occur at normal driving conditions.
By comparing the modeling performance of the
proposed MR damper model based on ANN with an-
other MR damper models presented in the literature,
it is considerable to assume an optimal modeling per-
formance. In the proposed ANN model, the obtained
modeling error of 7.25% based on the RMS is equiv-
alent to 4.7% of Error to Signal-Ratio (ESR), this
means that the error in the proposed ANN model
is: 1) lower than the ESR average (14.5%) obtained
by the Bingham model and reported in (Savaresi
et al., 2005); 2) lower than the ESR average (8.7%)
obtained by a phenomenological model reported in
(Ruiz-Cabrera et al., 2010); lower than the ESR av-
erage (38.7%) obtained by a semi-phenomenological
model reported in (Ruiz-Cabrera et al., 2010); but
greater than the ESR average of (0.9%) and (2%) ob-
tained by an ANN model reported in (Savaresi et al.,
2005) and (Ruiz-Cabrera et al., 2010) respectively.
Although these latter ANN structures have regressors,
use the output feedback and demand the displacement
and velocity sensor.
Due to reliability of the proposed MR damper
model and simplicity on the ANN structure, the model
can be used to test semiactive suspension control sys-
tems. A control technique free of model has been
used to control the semiactive suspension of a quar-
ter of vehicle system; the performance of the passive
suspension was used as benchmark. Simulation re-
sults show that passengers comfort and road holding
can be increased at least 7.4% and 40.4% respectively,
when an MR semiactive suspension is used.
ACKNOWLEDGEMENTS
Authors thank to CONACYT (Program of Postgradu-
ate Cooperation - 2010) for the financial supports of
this research.
REFERENCES
Ahn, K., Islam, M., and Truong, D. (2008). Hysteresis
modeling of magneto-rheological (mr) fluid damper
by self tuning fuzzy control. In ICCAS 2008, Seoul
Korea, pages 2628–2633.
Atray, V. and Roschke, P. (2003). Design, fabrica-
tion, testing and fuzzy modeling of a large magneto-
rheological damper for vibration control in a railcar.
In IEEE/ASME Joint Rail Conf., pages 223–229.
Boada, M., Calvo, J., Boada, B., and D´ıaz, V. (2011). Mod-
eling of a magnetorheological damper by recursive
lazy learning. International Journal of Non-Linear
Mechanics, 46:479–485.
C¸ esmeci, S. and Engin, T. (2010). Modeling and test-
ing of a field-controllable magnetorheological fluid
damper. International Journal of Mechanical Sci-
ences, 52(8):1036–1046.
Chang, C. and Zhou, L. (2002). Neural network emulation
of inverse dynamics for a magnetorheological damper.
Journal of Structural Engineering, 128(2):231–239.
Chen, E., Si, C., Yan, M., and Ma, B. (2009). Dy-
namic characteristics identification of magnetic rhe-
ological damper based on neural network. In Ar-
tificial Intelligence and Computational Intelligence,
2009, Shangai, China, pages 525–529.
Choi, S., Lee, S., and Park, Y. (2001). A hysteresis
model for field-dependent damping force of a mag-
netorheological damper. J. of Sound and Vibration,
245(2):375–383.
Dong, X., Yu, M., Liao, C., and Chen, W. (2010). Com-
parative research on semi-active control strategies for
magneto-rheological suspension. Nonlinear Dynam-
ics, 59:433–453.
Du, H., Szeb, K., and Lam, J. (2005). Semiactive h
1
con-
trol of vehicle suspension with magneto-rheological
dampers. J. of Sound and Vibration, 283:981–996.
Freeman, J. and Skapura, D. (1991). Neural Networks: Al-
gorithms, Applications and Programming Techniques.
Adisson-Wesley.
Gamota, D. and Filisko, F. (1991). Dynamic mechanical
studies of electrorheological materials: Moderate fre-
quencies. Journal of Rheology, 35:399–425.
Guo, S., Yang, S., and Pan, C. (2006). Dynamical modeling
of magneto-rheological damper behaviors. Int. Mater.,
Sys. and Struct., 16:3–14.
Hagan, M., Demuth, H., and Beale, M. (1996). Neural Net-
work Design. PWS Publishing.
Hong, K., Sohn, H., and Hedrick, J. (2002). Modi-
fied skyhook control of semi-active suspensions: A
new model, gain scheduling, and hardware-in-the-
loop tuning. J. Dyn. Sys., Meas., Control, 124(1):158–
167.
Korbicz, J., Koscielny, J., Kowalczuk, Z., and Cholewa,
W. (2004). Fault Diagnosis Models, Artificial Intel-
ligence, Applications. Springer.
Kwok, N., Ha, Q., Nguyen, T., Li, J., and Samali, B. (2006).
A novel hysteretic model for magnetorheological fluid
dampers and parameter identification using particle
MRDamperIdentificationusingANNbasedon1-Sensor-AToolforSemiactiveSuspensionControlCompliance
501

swarm optimization. Sensors and Actuators A: Physi-
cal, 132:441–451.
Lozoya-Santos, J., Morales-Menendez, R., and Ramirez-
Mendoza, R. (2009). Design of experiments for mr
damper modelling. In 17th Int. Joint Conf. on Neural
Networks, pages 1915–1922.
Metered, H., Bonello, P., and Oyadiji, S. (2010). The exper-
imental identification of magnetorheological dampers
and evaluation of their controllers. Mechanical Sys-
tems and Signal Processing, 24:976–994.
Poussot-Vassal, C., Sename, O., Dugard, L., G´asp´ar, P.,
Szab´o, Z., and Bokor, J. (2008). A new semi-active
suspension control strategy through lpv technique.
Control Engineering Practice, 16(12):1519–1534.
Ruiz-Cabrera, J., D´ıaz-Salas, V., Morales-Menendez, R.,
n´on, L. G.-C., and Ramirez-Mendoza, R. (2010).
Comparison of mr damper models. In 18th Mediter-
ranean Conference on Control and Automation, Mar-
rakech Morocco, June 23-25, pages 1509–1513.
Savaresi, S., Bittanti, S., and Montiglio, M. (2005). Iden-
tification of semi-physical and black-box non-linear
models: the case of mr-dampers for vehicles control.
Automatica, 41:113–127.
Sj¨oberg, J. (1995). Non-linear System Identification with
Neural Networks. PhD thesis, Link¨oping University,
Sweden.
Spelta, M., Savaresi, S., and Fabbri, L. (2010). Experi-
mental analysis of a motorcycle semi-active rear sus-
pension. Control Engineering Practice, article in
press:doi:10.1016/j.conengprac.2010.02.006.
Spencer, B., Dyke, S., Sain, M., and Carlson, J. (1996). Phe-
nomenological model of a mr damper. ASCE Journal
of Engineering Mechanics, 123(3):230–238.
Stanway, R., Sproston, J., and Stevens, N. (1987). Non-
linear modeling of an electrorheological vibration
damper. Journal of Electrostatics, 20:167–184.
Wang, L. and Kamath, H. (2006). Modeling hysteretic
behaviour in mr fluids and dampers using phase-
transition theory. Smart Mater. Struct., 15:1725–1733.
Yang, G., Jr., B. S., and Dyke, S. (2002). Large-scale mr
fluid dampers: Modeling and dynamic performance
considerations. Engineering Structures, 24:309–323.
Zapateiro, M., Luo, N., Karimi, H., and Veh´ı, J. (2009).
Vibration control of a class of semiactive suspension
system using neural network and backstepping tech-
niques. Mechanical Systems and Signal Processing,
23:1946–1953.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
502
