T-ACO Tournament Ant Colony Optimisation

for High-dimensional Problems

Emmanuel Sapin and Ed Keedwell

College of Engineering, Mathematics and Physical Sciences, University of Exeter, Harrison Building, Exeter, England, U.K.

Keywords:

Ant Colony Optimisation, Tournament Selection, High-dimensional Problem.

Abstract:

Standard ACO implementations use a roulette wheel to allow ants to make path decisions at each node of the

topology which works well for problems of smaller dimensionality, but breaks down when higher numbers of

variables are considered. Such problems are becoming commonplace in biology and particularly in genomics

where thousands of variables are considered in parallel. In this paper, a tournament-based ACO approach is

proposed that is shown to outperform the roulette wheel-based approach for all problems of higher dimen-

sionality in terms of the performance of the ﬁnal solutions and execution time on problems taken from the

literature.

1 INTRODUCTION

NP-hard combinatorial problems are an important

class of problems in theoretical and real-world tasks.

For these problems no algorithm can solve them in a

polynomial time. Examples of such problems are the

bin packing problem and the knapsack problem.

Some recent approaches to solve these problems

are to use nature inspired or other stochastic algo-

rithms that are known to have delivered good results

for this class of problems. Ant colony optimisation

(ACO), as one such algorithm is inspired by the way

in which ants in the wild ﬁnd the shortest path to food

using pheromones. ACO has been shown to deliver

excellent results on discrete combinatorial test prob-

lems (Dorigo and Caro, 1999) and has been widely

applied to real-world problems ranging from water

distribution system optimisation (Zecchin et al., 2007;

St¨utzle and Dorigo, 1999) to bioinformatics (Christ-

mas et al., 2011; Moore, 2005; Greene et al., 2008).

In particular, there are a number of recent appli-

cations of ACO to the discovery of gene-gene inter-

actions in genomic data. The problem is to search a

large database (up to 400,000) of small DNA changes

known as single nucleotide polymorphisms (SNPs),

and ﬁnd the SNP or combination of SNPs that best

discriminates between diseased and healthy individ-

uals (for a more in-depth discussion of the problem,

readers are directed to (Christmas et al., 2011)). The

sheer size of the data presents a unique challenge to

ACO as there are many thousands of possible choices

for each ant at each decision point. Paths are usu-

ally chosen through the use of a roulette wheel which

weights decisions based on the level of pheromone for

each SNP. This procedure works well for small num-

bers of decision variables, but as we will show the

performance of the roulette wheel breaks down when

many thousands of path choices are included and a

new method based on a tournament is investigated.

The idea of using a tournament for this purpose

was ﬁrst proposed in (Tsai et al., 2002), who used the

method in conjunction with other algorithm modiﬁca-

tions to cluster data. We extend their work here by in-

vestigating solely the impact of tournament selection

on a widely recognised problem taken from the lit-

erature, and determine the robustness of the improve-

ment with respect to a variety of algorithm parameters

and problem sizes.

The selection procedure in evolutionary algo-

rithms is closely related to path choices in ACO as

both procedures are required to provide a stochastic

decision but one that is weighted towards individu-

als with the greatest ﬁtness, or paths with the greatest

pheromone. Tournament selection is often preferred

over the roulette wheel in evolutionary computing for

a number of reasons, including its comparative ease

of implementation, computational efﬁciency, the ease

with which selection pressure can be modiﬁed and

perhaps most importantly, its robustness with respect

to the distribution of the ﬁtness function. Roulette

wheels do not function well where the distribution of

ﬁtness (pheromone) is highly skewed or where neg-

Sapin E. and Keedwell E..

T-ACO Tournament Ant Colony Optimisation for High-dimensional Problems.

DOI: 10.5220/0004159900810086

In Proceedings of the 4th International Joint Conference on Computational Intelligence (ECTA-2012), pages 81-86

ISBN: 978-989-8565-33-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

ative ﬁtnesses exist. Although negative pheromone

is not a concern in ACO, the remaining beneﬁts to

evolutionary computing should translate to ACO with

the use of a tournament in place of the roulette wheel

for path selection. T-ACO replaces the roulette wheel

with a tournament in path selection in ACO.

The following sections describe the implementa-

tion of the algorithm, experimentation with knapsack

problems of varying sizes and multiple parameter set-

tings, and concluding remarks.

2 METHOD

2.1 Standard ACO

The standard ant colony optimisation (Dorigo and

Caro, 1999) creates a population of agents ants that

traverse a topology. The topology can reﬂect the un-

derlying topology of the problem (e.g. with the travel-

ling salesman problem) or can make use of a construc-

tion graph where each variable choice is aligned with

connections between variable choices forming the set

of paths for the algorithm to traverse. Construction

graphs are used for problems that do not have a na-

tive topology and in this way, any discrete combina-

torial problem is solvable with ACO. Ants make path

choices at each juncture in the graph based on the

level of pheromone (and occasionally local heuristic

values) on the paths leading to the next variable se-

lection. However, a further modiﬁcation is desirable

where the selection of subsets of variables is required

and the order of variable selection is not important

(e.g. in the knapsack and genomics problems). In

this case, a full construction graph is not required and

pheromone can be deposited on the variables them-

selves, using the approach described in (Leguizam´on

and Michalewicz, 1999), which is used here.

The probability of selecting a variable can be calcu-

lated thus:

(t) =

[τ

(t)]

.[η

(t)]

∑

h∈J

[τ

(t)]

.[η

(t)]

(1)

Where τ

(t) is the pheromone on the variable i at time

t and η

(t) is the local heuristic value (optional) on the

same variable. α and β coefﬁcients allow the balance

between the two components to be adjusted.

Once an ant reaches its destination, it leaves

pheromone on the chosen variables that reﬂect the

quality of the solution that the variables represent.

Pheromone is then evaporated by a ﬁxed percentage

across all variables and the algorithm iterates again.

The updated pheromone can therefore be calculated

thus:

(t + 1) = (1− ρ).τ

(t) + ∆

(t) (2)

Where ρ is the pheromone evaporation rate (typi-

cally between 1 and 10%) and ∆

(t) is the additional

pheromone laid by the ants traversing the graph.

2.2 Tournament-ACO

T-ACO uses the above standard equations (without

local heuristic) as the basis for its algorithm. The

key difference between T-ACO and ACO is how the

variable is selected for a given set of probabilities.

Traditionally this is achieved by summing the prob-

abilities as calculated above and selecting randomly

from these summed probabilities to determine the

next variables chosen by the ant. This process al-

lows the ant to choose randomly but with a deci-

sion weighted towards those variables with greater

pheromone values. T-ACO differs in that a tourna-

ment selection is used.

In this process, t variables are randomly chosen

from the set of possible variable choices and the vari-

able with the highest pheromone value is selected. By

varying t the greediness of the algorithm can be mod-

iﬁed, lower values of t approximates random search

as the competition element of the tournament is less-

ened and the inﬂuence of paths with high pheromone

is reduced. Higher values of t increase the greediness

of the search.

It should be noted that no such mechanism exists

for roulette wheel based search and the greediness of

the algorithm is usually adjusted through modiﬁca-

tions of the evaporation rate.

T-ACO therefore runs as follows

Initialise pheromone;

Repeat

For all the NBANT ants:

Choose items:

Repeat

Select NBT items according to the

tournament

Store the items the ant has chosen

For all the NBANT ants:

Calculate the fitness depending of the

value of the chosen items

Store the best fitness

Update pheromone of the chosen items

For all items: apply evaporation rate E

End

Where:

• NBANT: the numbers of ants of the algorithm;

• E: the evaporation rate in percentage;

• NBT: the number of paths for the tournament of

the selection process;

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

Figure 1 shows a ﬂow chart describing the method.

Figure 1: Flow chart describing the method.

The standard ACO algorithm with a roulette wheel

was also implemented for comparison.

2.3 Knapsack Problem

The Knapsack problem was chosen for experimenta-

tion as it is an NP-hard combinatorial problem which

has the required ﬂexibility in terms of the number of

decision variables. This problem has been studied

for more than one century and was introduced by the

mathematician Tobias Dantzig.

The problem is described as follows: given a set of

items, each with a weight and a value, determine the

count of each item to include in a collection so that

the total weight is less than or equal to a given limit

and the total value is as large as possible. It derives

its name from the problem faced by someone who is

constrained by a ﬁxed-size Knapsack and must ﬁll it

with the most useful items.

The problem is represented to the algorithm as

a construction graph of N columns (where N is the

number of variables), each with two nodes represent-

ing the binary decision of whether to pack the item or

not. The ﬁtness function is the sum of the values of

the selected items and the level of pheromone left by

each ant is the value of the ﬁtness function.

3 EXPERIMENTATION

3.1 Parameters of the Problem

A variety of parameters are modiﬁed to determine the

efﬁcacy of the proposed T-ACO approach. The main

objective is to show the effect that the tournament has

over varying problem sizes up to the large-scale deci-

sions required for processing genomic data.

Each item has a weight between 0 and 100 and a value

between 0 and 100. The knapsack capacity is 1000.

3.2 Parameters of the T-ACO

In order to solve the Knapsack problem, various pa-

rameter combinations for the ant colony optimisation

have been tested. The algorithm is described with the

three following parameters: The following evapora-

tion rates, E, have been tested: 1%, 10%, 25% and

50%. The followingnumbers of ants in the population

have been tested 50, 200, 500, 2 000 (NBANT). The

following selection process have been tried Roulette

wheel, tournament with 2%, 5%, 10% and 20 %.

A Monte Carlo method has also been implemented

in which random solutions are generated to act as a

benchmark.

3.3 Various Values of Parameters

All the combinations of values have been tried for the

three variables: the four evaporation rates E, the four

numbers of ants in the population NBANT and the

four sizes of the tournament NBT. For every com-

bination 50 runs are performed. An average of the

ﬁtness of the best individual is taken into account.

The ﬁrst experiment is designed to explore the po-

tential for tournament selection of variables in a high

(400,000) dimensional problem. The ﬁve curves in

ﬁgure 2, correspond to four tournament in the selec-

tion process and a roulette wheel selection. The X

axis is the number of ants in the colony and the Y

axis is the average of 200 best results (50 runs of the

algorithm with four different evaporation rates).

Figure 2: Variation of the ﬁtness depending on the number

of ants in the colony for various selection processes.

T-ACOTournamentAntColonyOptimisationforHigh-dimensionalProblems

This ﬁgure shows that for large-scale problems,

the roulette wheel is outperformed by all of the tour-

nament path selectors for all numbers of ants in the

population. It is interesting to note that the perfor-

mance of smaller tournaments increases in relation

to the number of ants whereas the larger tournament

(100) decreases in performance.

In ﬁgure 3, the ﬁve curves correspond to four numbers

of items in the selection process and a roulette wheel

selection. The X axis represents the evaporation rates

and the Y axis represents the average of 200 best re-

sults (50 runs of the algorithm, four possible numbers

of ants in the colony).

Figure 3: Variation of the ﬁtness depending on the evapora-

tion rate for various selection processes.

Figure 3 shows that for a variety of evaporation

rates, the effect of roulette wheel and tournament se-

lection processes is reasonably static. However, the

tournament always outperforms the roulette wheel ap-

proach.

3.4 Various Sizes of Problem

The following experiment explores all the combina-

tions of values of the three variables E, NBANT and

NBT, for various sizes of problems. The sum of the

ﬁtness of the best individual for all the runs is shown.

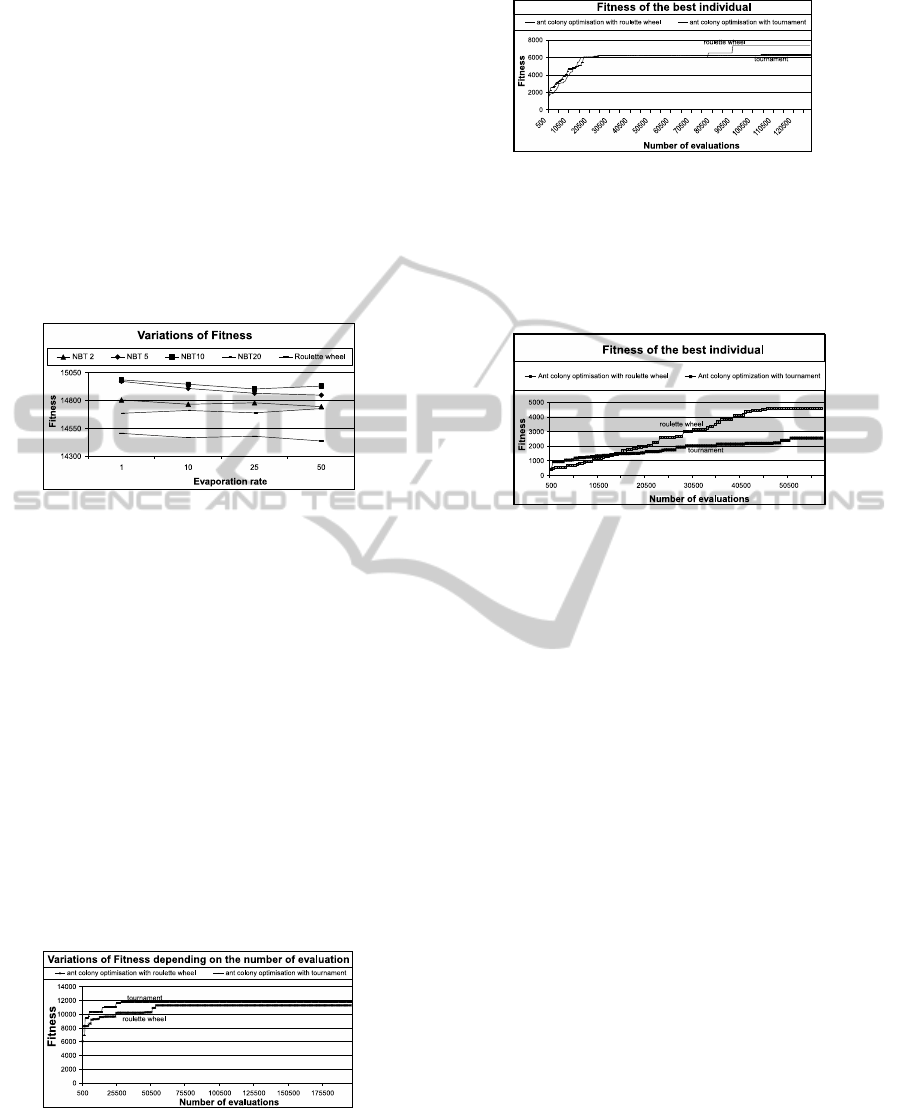
For 40,000 items, the graph in ﬁgure 4 is the sum of

ﬁtnesses of the best individuals. The X axis is the

number of evaluations of an individual.

Figure 4: Average of the ﬁtness of the best individuals de-

pending on the number of evaluations.

For 4000 items, the graph in ﬁgure 5 is the sum of

ﬁtnesses of the best individuals. The X axis is the

number of evaluations of an individual.

Figure 5: Average of the ﬁtness of the best individuals de-

pending on the number of evaluations.

For 400 items, the graph in ﬁgure 6 is the sum of ﬁt-

nesses of the best individuals. The X axis is the num-

ber of evaluations of an individual.

Figure 6: Average of the ﬁtness of the best individuals de-

pending on the number of evaluations.

Figure 4 shows that for large-scale problems, tour-

nament selection outperforms roulette wheel selec-

tion for the majority of the optimisation runs. This

advantage however, is diminished for 4000 items, in

ﬁgure 5, where the roulette wheel has the advantage.

Furthermore for just 400 items, the roulette wheel is

clearly the preferred method of selection for the paths

in ACO, ﬁgure 6.

Figure 7 shows the ﬁtness of a best individual for 100,

1000, 5000, 10000 and 100000 items. The X axis is

the ﬁtness of the best individual and the Y axis is the

number of items. This ﬁgure shows the performance

of a variety of tournament sizes, expressed as a per-

centage of the population size and the roulette wheel

selector across a number of problem sizes.

Figure 7 shows that whilst roulette wheel is the dom-

inant search procedure for problem sizes < 5000, the

tournament selectors become more successful as the

problem size increases. A tournament of approxi-

mately 5% appears to produce reasonable results in

all circumstances and it is interesting to note that the

tournament of 2% shows an almost opposite trajec-

tory to the roulette wheel search, improving consis-

tently as the problem size increases.

3.5 Execution Time

A further consideration with large-scale data is the

time taken to perform the selection process. As a

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

Figure 7: Fitness of a best individual depending on the num-

ber of evaluations.

highly repeated function within the algorithm, even

small differences in execution time will make a large

difference to the overall execution time of the algo-

rithm.

Figure 8 shows the comparison between runtimes for

roulette wheel and a tournament size of 10% of the

problem size. This is the complete execution time,

including the calculation of the objective function, so

it can be seen that the variable selection process has

a large impact on the complexity of the ant colony

optimisation algorithm.

Figure 8: A comparison of execution times on four different

problem sizes.

4 DISCUSSION

Roulette wheel path selection appears to be the

favoured process for problems of small dimensional-

ity, but above 1000 variables, the advantage switches

in favour of the tournament selection in terms of per-

formance on the knapsack problem. This can be ex-

plained by the fact that even large tournaments are

slower to converge on a solution in large spaces than

the roulette wheel approach. This effect appears to

be robust as it is unaffected by the modiﬁcation of a

number of other parameter modiﬁcations, including

evaporation rates and population sizes. An additional

advantage to the tournament-based approach is its rel-

ative speed at high dimensionalities. As the problem

sizes increase, the process of creating a roulette wheel

becomes more inefﬁcient, whereas the tournamentap-

proach even with a tournament size related to the size

of the problem increases far more slowly.

Figure 8 shows for a problem size of 1000 variables,

the tournament is approximately 1.5 times faster than

the roulette wheel, but for 100,000 variables, this in-

creases to 20 times faster. The ability for the tourna-

ment selector to scale to larger sets of decision vari-

ables is vital in application areas where larger prob-

lem sizes will require longer runs of the algorithm.

In many applications the objective function forms the

largest part of the computational load, but neverthe-

less, an approach that both increases performance and

reduces computational load in these high dimensions

is signiﬁcant.

The best result was obtained for 500 ants, 20 items in

the tournament of the selection process and an evapo-

ration rate of 1%.

5 CONCLUSIONS

A tournament-based ACO algorithm known as T-

ACO was implemented and experiments were con-

ducted on a variety of problem sizes and algorithm

parameter settings. From this it is proposed that for

problems of higher dimensionality, the use of a tour-

nament approach provides better results and reduced

computational time. This is likely to be particularly

useful for high-dimensional problems in genomics

where the number of discrete variables is very large

and the computational load is high. In further work

we hope to apply this algorithm to real-world optimi-

sation problems, including those in bioinformatics to

further test the validity of the T-ACO approach.

REFERENCES

Christmas, J., Keedwell, E., Frayling, T., and Perry, J.

(2011). Ant colony optimisation to identify genetic

variant association with type 2 diabetes,. In Informa-

tion Sciences., volume 181, pages 1609–1622.

Dorigo, M. and Caro, G. D. (1999). The ant colony opti-

mization meta-heuristic. In in New Ideas in Optimiza-

tion, pages 11–32. McGraw-Hill.

Greene, C., White, B., and Moore, J. (2008). Ant colony

optimization for genome-wide genetic analysis. In

Dorigo, M., Birattari, M., Blum, C., Clerc, M., Sttzle,

T., and Winﬁeld, A., editors, Ant Colony Optimiza-

tion and Swarm Intelligence, volume 5217 of Lecture

Notes in Computer Science, pages 37–47. Springer

Berlin / Heidelberg.

Leguizam´on, G. and Michalewicz, Z. (1999). A new ver-

sion of ant system for subset problems. In Angeline,

T-ACOTournamentAntColonyOptimisationforHigh-dimensionalProblems

P. J., Michalewicz, Z., Schoenauer, M., Yao, X., and

Zalzala, A., editors, Proceedings of the Congress on

Evolutionary Computation, volume 2, pages 1459–

1464, Mayﬂower Hotel, Washington D.C., USA.

IEEE Press.

Moore, J. H. (2005). A global view of epistasis. Nat Genet,

37(1):13–14.

St¨utzle, T. and Dorigo, M. (1999). Aco algorithms for

the traveling salesman problem 1999. In Periaux

(eds), Evolutionary Algorithms in Engineering and

Computer Science: Recent Advances in Genetic Algo-

rithms, Evolution Strategies, Evolutionary Program-

ming, Genetic Programming and Industrial Applica-

tions.

Tsai, C.-F., Wu, H.-C., and Tsai, C.-W. (2002). A new data

clustering approach for data mining in large databases.

In ISPAN, pages 315–320.

Zecchin, A., Maier, H., Simpson, A., M.Leonard, and

Nixon, J. (2007). Ant colony optimization applied to

water distribution system design: Comparative study

of ﬁve algorithms. In Journal of Water Resources

Planning and Management, Vol. 133, No. 1, January

IJCCI2012-InternationalJointConferenceonComputationalIntelligence