
Transonic Wing Optimization by Variable-resolution Modeling
and Space Mapping
Eirikur Jonsson, Leifur Leifsson and Slawomir Koziel
Engineering Optimization & Modeling Center, School of Science and Engineering, Reykjavik University, Reykjavik, Iceland
Keywords:
Transonic Wing Design, CFD, Surrogate-based Optimization, Variable-resolution Modeling, Space Mapping.
Abstract:
This paper presents an efficient aerodynamic design optimization methodology for wings in transonic flow.
The approach replaces the computationally expensive high-fidelity CFD model in an iterative optimization
process with a corrected polynomial approximation model constructed by a cheap low-fidelity CFD model.
The output space mapping technique is used to correct the approximation model to yield an accurate predictor
of the high-fidelity one. Both CFD models employ the RANS equations with the Spalart-Allmaras turbulence
model, but the low-fidelity one uses a coarse mesh resolution and relaxed convergence criteria. Our method
is applied to a constrained lift maximization of a rectangular wing at transonic conditions with 3 design vari-
ables. The optimized designs are obtained by using 50 low-fidelity CFD model evaluations to set up the
approximation model and 7 to 8 high-fidelity model evaluations, equivalent to around 10 high-fidelity CFD
model evaluations.
1 INTRODUCTION
The wing is the most important component of an air-
craft, significantly affecting its overall performance.
As the wing provides lift, it is at the same time the
main source of drag, responsible for about 2/3 of the
total drag of the aircraft (Raymer, 2006). Reducing
this wing drag by a better design, and, hence, mini-
mizing cost, is often the primary objective of modern
aircraft design.
Nowadays, aerodynamic design using high-
fidelity computational fluid dynamic (CFD) models
is ubiquitous and plays an important role in aircraft
development. Traditional design optimization tech-
niques, such as gradient-based or population-based
ones, involve a large number of simulations. Conse-
quently, direct aerodynamic optimization with high-
fidelity CFD models using traditional optimization
techniques is impractical, even when using cheap ad-
joint sensitivities.
One of the overall objectives of surrogate-based
optimization (SBO) (Queipo et al., 2005; Forrester
and Keane, 2009) is to reduce the number of evalu-
ations of expensive simulations, thereby making the
design process more efficient. This is achieved by an
iterative correction-prediction process where a surro-
gate model (a computationally cheap representation
of the high-fidelity one) is constructed and subsequen-
tly exploited to obtain approximate location of the
high-fidelity model optimal design. The surrogate
model can be constructed by approximating sampled
high-fidelity model data using, e.g., polynomial ap-
proximation (Queipo et al., 2005), radial basis func-
tions (Forrester and Keane, 2009; Wild et al., 2008),
kriging (Koziel et al., 2011; Simpson et al., 2001;
Journel and Huijbregts, 1978; O’Hagan and King-
man, 1978), neural networks(Haikin, 1998; Min-
sky and Papert, 1969), or support vector regression
(Smola and Sch
¨
olkopf, 2004) (response surface ap-
proximation surrogates) or by correcting/enhancing
a physics-based low-fidelity model (physical surro-
gates) (Søndergaard, 2003) .
Approximation surrogates usually require a sig-
nificant number of high-fidelity model evaluations to
ensure decent accuracy. Furthermore, the number of
samples typically grows exponentially with the num-
ber of design variables. On the other hand, approx-
imation surrogates can be a basis of efficient global
optimization techniques (Forrester and Keane, 2009).
Various techniques of updating the training data set
(so-called infill criteria (Forrester and Keane, 2009))
have been developed that aim at obtaining global
modeling accuracy, locating globally optimal design,
or the trade-offs between the two, particularly in the
context of kriging interpolation (Forrester and Keane,
2009).
489
Jonsson E., Leifsson L. and Koziel S..
Transonic Wing Optimization by Variable-resolution Modeling and Space Mapping.
DOI: 10.5220/0004164004890498
In Proceedings of the 2nd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SDDOM-2012), pages
489-498
ISBN: 978-989-8565-20-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

Physics-based surrogate models are not as versatile
as approximation ones because they rely on an un-
derlying low-fidelity model (a simplified description
of the system under consideration), typically prob-
lem specific. The physics-based models can be ob-
tained by a number of ways, such as by neglecting
certain second-order effects, using simplified equa-
tions, or, which is probably the most versatile ap-
proach, by exploiting the same CFD solver as used
to evaluate the high-fidelity model but with coarser
mesh and/or relaxed convergence criteria (so called
variable-resolution modeling) (Leifsson and Koziel,
2011b). The physics-based surrogate models contain
knowledge about the system of interest. Due to this,
a limited amount of high-fidelity model data is nec-
essary to ensure a required accuracy of the surrogate.
For the same reason, these physics-based models have
good generalization capabilities.
There have been proposed several SBO algo-
rithms using physics-based surrogates in the litera-
ture, including the approximation and model manage-
ment optimization (AMMO) (Alexandrov and Lewis,
2001), space mapping (SM) (Bandler et al., 2004;
Koziel et al., 2008), manifold mapping (MM) (Echev-
erria and Hemker, 2005), and, more recently, the
shape-preserving response prediction (SPRP) (Leifs-
son and Koziel, 2011a). All of these methods differ in
a specific way of how the low-fidelity model is used
to construct the surrogate. Space mapping is proba-
bly the most popular approach of this kind. It was
originally developed for simulation-driven design in
microwave engineering (Bandler et al., 2004) how-
ever, it is currently becoming more and more popular
in other areas of engineering and science (cf. Refs.
(Bandler et al., 2004; Koziel et al., 2008), and refer-
ences therein). Despite its potential, space mapping
has not become popular in aerodynamic shape opti-
mization. The only work reported so far is by Robin-
son et al. (Robinson et al., 2006), where the so-called
corrected SM was applied, among other methods, to
airfoil design, however no significant design speed up
has been reported.
In this paper, we develop a space mapping al-
gorithm for the aerodynamic design optimization
of wings in transonic flow. In particular, we ex-
tend our recently developed algorithm for airfoils in
two-dimensional transonic flow (Koziel and Leifs-
son, 2012) which employed variable-resolution mod-
els and output space mapping (Bandler et al., 2004;
Koziel et al., 2008). The algorithm proposed in
this work handles three-dimensional flow past wings.
The complicated fluid flow analysis includes a cer-
tain level of numerical noise. To overcome associ-
ated problems, we have replaced the direct use of low-
fidelity models by approximation models. We demon-
strate the effectiveness of the algorithm by a couple of
numerical examples involving constrained lift maxi-
mization.
2 CFD MODELING
In this section, we present the CFD model. In partic-
ular, the governing equations, geometry and grid gen-
eration are presented. We, furthermore, present the
results of a grid convergence study and model valida-
tion.
2.1 Governing Equations
Commercial transport aircraft operate in the transonic
flow regime where the flow is compressible. We as-
sume that the fluid is air modelled by the ideal gas
law and the Sutherland law for dynamic viscosity µ.
The flow is assumed to be steady, viscous, and with-
out body forces, mass-diffusion, chemical reactions
or external heat addition. We solve the RANS equa-
tions with the one equation Spalart-Allmaras turbu-
lence model (Tannehill et al., 1997).
2.2 Wing Geometry
In this work, we consider a simple constant chord
wing. The wing is constructed by two NACA four
digit airfoils (Abbott and Von Doenhoff, 1959), one
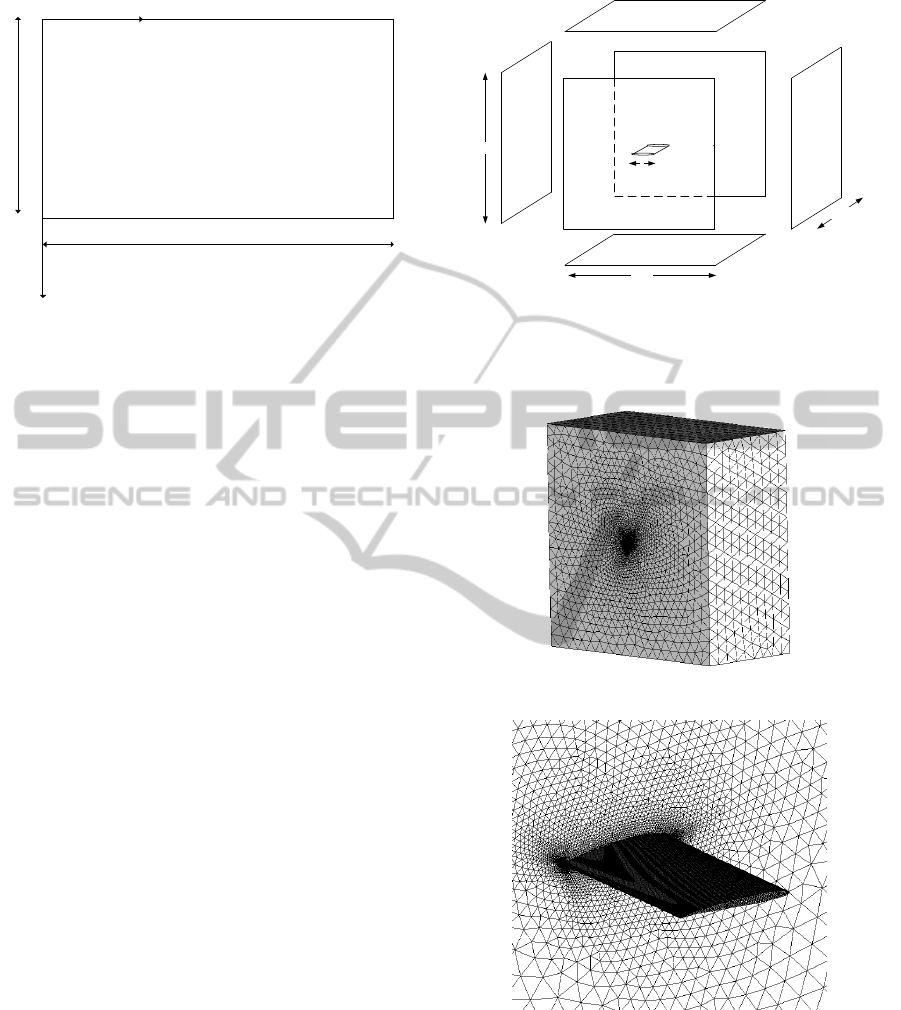
at the root and the other at the tip as shown in Fig. 1.
Three parameters define each airfoil section, namely
the maximum ordinate of the mean camberline as a
fraction of chord (m), the chordwise position of the
maximum ordinate (p), and the thickness-to-chord ra-
tio (t/c) (see Abbott and von Doenhoff (Abbott and
Von Doenhoff, 1959) for details). The reason for
choosing these particular airfoils and the wing geom-
etry is to limit the number of design variables in our
initial study.
2.3 Computational Grid
The farfield is configured in a box topology where the
wing root airfoil is place in the center of the symme-
try plane with its leading edge placed at the origin
(x,y,z) = (0, 0,0). The farfield extends 100 chord
lengths, 100c, in all directions from the wing, up-
stream, above, below and aft of the wing where the
maximum element size in the flow domain is 11 chord
lengths or 11c. The computational domain is shown
in Fig. 2.
SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
490
x
y
1
2
b/2
Wing Root
NACA mpxx airfoil 1
Wing Tip
NACA mpxx airfoil 2
c
Figure 1: A planform view of a constant chord wing used
in this work. The rectangular wing is constructed by two
NACA airfoils, shown at spanstations 1, the wing root, and
2, the wing tip. Each airfoil has its own set of design pa-
rameters. The wing semispan is b/2.
An unstructured tri/tetra shell grid is created on
all surfaces. The shell grid from the wing is then ex-
truded into the volume where the volume is flooded
with tri/tetra elements. The grid is made dense close
to the wing where it then gradually grows in size as
moving away from the wing surfaces. To capture the
viscous boundary layer an inflation layer or a prism
layer is created on the wing surfaces as well. In the
stream-wise direction, the number of elements on the
wing is set to 100 on both upper and lower surface.
The bi-geometric bunching law with a growth ratio of
1.2 is employed in the stream-wise direction over the
wing to obtain a more dense element distribution at
the leading edge and the trailing edge. This is done
in order to capture the high pressure gradient at the
leading edge and the separation at the trailing edge.
The minimum element size of the wing in the stream-
wise direction is set to 0.1%c, and it is located at the
leading and trailing edge. In the span-wise direction
elements are distributed uniformly and number of el-
ements set to 100 over the semi-span. A prism layer
is used to capture the viscous boundary layer. This
layer consists of a number of structured elements that
grow in size normal to the wing surface into the do-
main volume. The inflation layer has a initial height
of 5 ×10
−6
c where it is grown 20 layers into the vol-
ume using a exponential growth law with ratio of 1.2.
The initial layer height is chosen so that y
+
< 1 at
all nodes on the wing. The resulting grid is shown in
Fig. 3.
2.4 Flow Solver
The numerical fluid flow simulations are performed
using the computer code ANSYS FLUENT (ANSYS,
200 c
200 c
c
Symmetry 100 c
PF
PF
PF
PF
Pressure Farfield (PF)
Figure 2: A sketch of the computational domain. All bound-
aries are set as pressure-farfield (PF), a side from the wing
surface, which is a wall type. Symmetry is applied through
the wing center. The wing chord length is denoted by c.
(a)
(b)
Figure 3: A view of of the computational grid, (a) the
farfield grid, and (b) a close-up of the wing shell grid.
2010). The implicit density-based solver is applied
using the Roe-FDS flux type. The spatial discretiza-
tion schemes are set to second order for all vari-
ables, and the gradient information is found using
the Green-Gauss node based method. The residuals,
which are the sum of the L
2
norm of all governing
Transonic Wing Optimization by Variable-resolution Modeling and Space Mapping
491

equations in each cell, are monitored and checked for
convergence. The convergence criterion for the high-
fidelity model is such that a solution is considered to
be converged if the residuals have dropped by six or-
ders of magnitude, or the total number of iterations
has reached 1000. Also, the lift and drag coefficients
are monitored for convergence.
To reflect the compressible nature of this prob-
lem, two types of boundaries are used. The pressure-
farfield is applied to the boundary on all surfaces, ex-
cept where the wing penetrates the symmetry bound-
ary. The boundary types is shown in Fig. 2.
Air is the working fluid at compressible tran-
sonic conditions. The free-stream Reynolds number
is Re
∞,S
= 11.72 × 10
6
, where S is the reference area,
which in this case is planform area. The Mach number
is set to M
∞
= 0.8395 and the angle of attack is set to
α = 0
◦
. We assume that the flow is calm at its bound-
aries and turbulent viscosity ratio set to µ
t
/µ
∞
= 1.
Furthermore, the boundary pressure and temperature
is set to p
∞
= 80507.2 Pa and T
∞
= 255.6 K.
2.5 Grid Convergence
A grid convergence study is conducted using the ON-
ERA M6 wing (NASA, 2008). The flow past the ON-
ERA M6 wing is simulated at various grid resolutions
at Re
∞,c
mac
= 11.72 × 10
6
, M
∞
= 0.8395 and angle
of attack α = 3.06
◦
, where c
mac
is the mean aerody-
namic chord length. The flow conditions are selected
to match experimental flow conditions of an ONERA
M6 wing experiment 2308 conducted by Schmitt, V.
and F. Charpin (Schmitt and Charpin, 1979), see Sec-
tion 2.6.
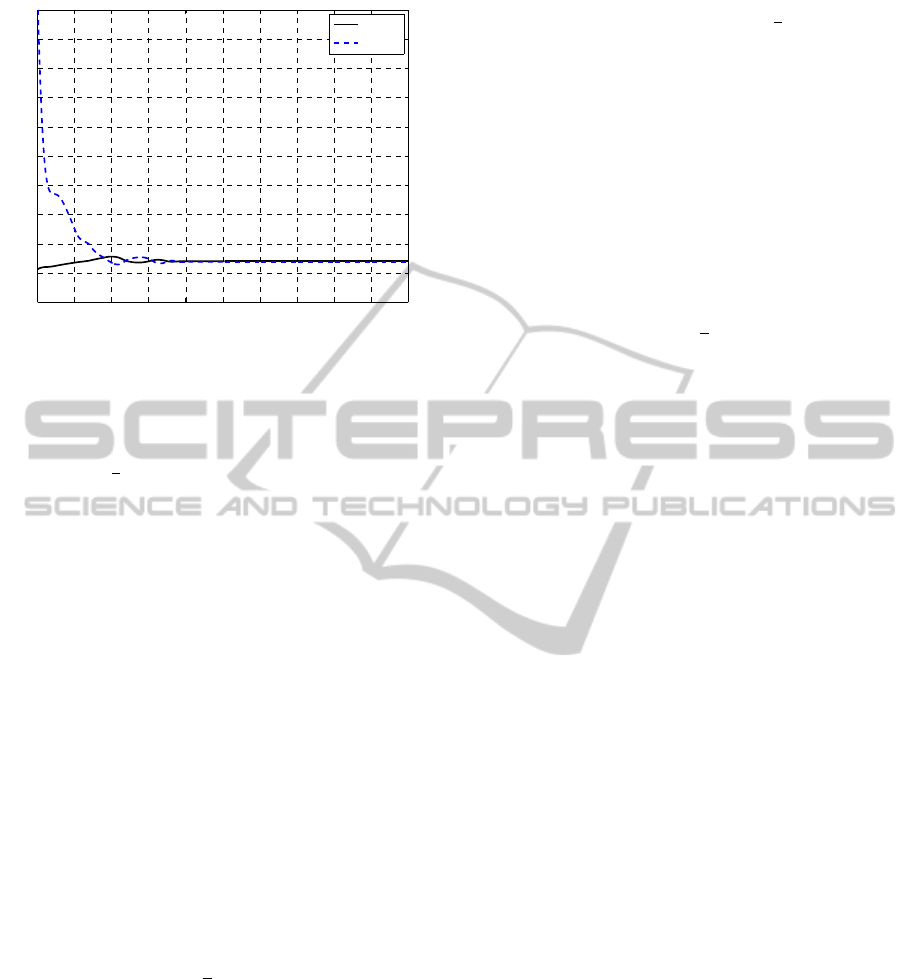
The grid convergence study shown in Fig. 4(a)
revealed that 1,576,413 cells are needed for conver-
gence in lift. The drag, however, can still be improved
as evident from Fig. 4(a), where convergence has not
been reached due to limitations in the computational
resources. We proceed, however, with this grid as
the high-fidelity model grid. The overall simulation
time needed for one high-fidelity CFD simulation was
around 223 minutes, as shown in Fig. 4(b), executed
on four Intel-i7-2600 processors in parallel. This exe-
cution time is based on 1000 solver iterations, where
the solver terminated due to the maximum number of
iterations limit.
2.6 Model Validation
The ONERA M6 wing is a commonly used CFD val-
idation case for external flows because of its simple
geometry combined with complexities of transonic
flow, i.e., local supersonic flow, shocks, and turbu-
10
4
10
5
10
6
10
7
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
Number of grid elements
C
L
,10 x C
D
C
L
10 x C
D
(a)
10
4
10
5
10
6
10
7
0
50
100
150
200
250
300
Number of grid elements
Time [min]
(b)
Figure 4: Grid convergence study using the ONERA M6
wing at Re
∞,c
mac
= 11.72 × 10
6
, M
∞
= 0.8395 and angle of
attack α = 3.06
◦
. (a) Lift (C
L
) and drag (C
D
) coefficients
versus the number of grid elements, and (b) simulation time
versus the number of grid elements.
lent boundary layers with separation. We consider
the ONERA M6 wing as a validation case for the
high-fidelity CFD model. The ONERA M6 wing
is a swept, semi-span wing with no twist and then
symmetrical ONERA D airfoil section (Schmitt and
Charpin, 1979). The numerical coordinates of the
airfoil section at the y/(b/2) = 0 are obtained from
NASA (NASA, 2008). The coordinates indicate that
there is a finite thickness to the trailing edge. In this
work, we use a zero trailing edge thickness. The air-
foil coordinates are linearly scaled near the trailing
edge so that the trailing edge thickness is zero. We
use experimental data from a ONERA M6 wing wind
tunnel experiment 2308 conducted by Schmitt, V. and
F. Charpin (Schmitt and Charpin, 1979). The solver is
configured to match the experimental flow conditions
which are Re
∞,c
mac
= 11.72 × 10
6
, M
∞
= 0.8395, an-
gle of attack α = 3.06
◦
, pressure p
∞
= 80507.2Pa and
SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
492
temperature T
∞
= 255.6K.
The available experimental data obtained by
Schmitt and Charpin, consists of pressure distribu-
tions (C
p
) at seven cross-sections along the span,
namely, y/(b/2) = 0.2, 0.44, 0.65, 0.8, 0.9, 0.95, 0.99.
The CFD simulation results are shown for y/(b/2) =
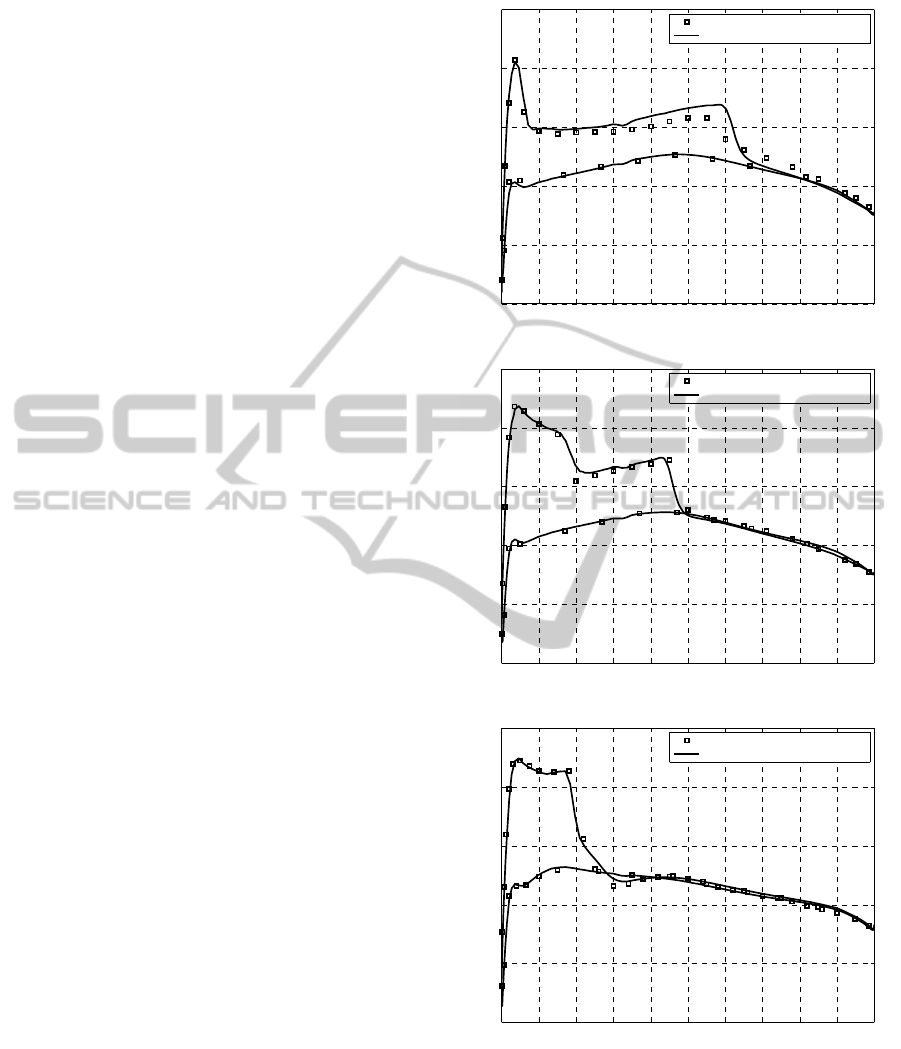
0.2, 0.65, 0.95, in Fig. 5. Inspecting the results, we
see that the correlation between the CFD simulation
and experimental data is excellent.
3 OPTIMIZATION WITH SPACE
MAPPING
In this paper, the wing design is carried out in a com-
putationally efficient manner by exploiting the space
mapping (SM) methodology (Bandler et al., 2004).
Space mapping replaces the direct optimization of an
expensive (high-fidelity or fine) airfoil model f ob-
tained through high-fidelity CFD simulation, by an it-
erative updating and re-optimization of a cheaper sur-
rogate model s. The key component of SM is the
physics-based low-fidelity (or coarse) model c that
embeds certain knowledge about the system under
consideration and allows us to construct a reliable sur-
rogate using a limited amount of high-fidelity model
data. Here, the low-fidelity model is evaluated using
the same CFD solver as the high-fidelity one, so that
both models share the same knowledge of the wing
performance.
3.1 Optimization Problem
The simulation-driven design can be generally formu-
lated as a nonlinear minimization problem
x
∗
= arg min
x
H ( f (x)), (1)
where x is a vector of design parameters, f the high-
fidelity model to be minimized at x and H is the ob-
jective function. x
∗
is the optimum design vector.
The high-fidelity model will represent aerodynamic
forces, lift and drag coefficient, as well as other scalar
responses such as cross-sectional area A of the wing at
interesting location. Area response can be of a vector
form A if one requires multiple area cross-sectional
constraints at various locations on the wing, e.g., the
wing root and the wing tip. The response will have to
form
f (x) = [C
L, f
(x),C
D, f
(x),A
f
(x)]
T
, (2)
where C
L, f
and C
D, f
are the lift and drag coefficient
for a three-dimensional wing, respectively, generated
by the high-fidelity model. We are interested in the
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
−1.5
−1
−0.5
0
0.5
1
x/c
C
p
3D Schmitt, V. and F. Charpin Data
3D CFD Simulation
(a) y/(b/2) = 0.2.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
−1.5
−1
−0.5
0
0.5
1
x/c
C
p
3D Schmitt, V. and F. Charpin Data
3D CFD Simulation
(b) y/(b/2) = 0.65.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
−1.5
−1
−0.5
0
0.5
1
x/c
C
p
3D Schmitt, V. and F. Charpin Data
3D CFD Simulation
(c) y/(b/2) = 0.95.
Figure 5: Pressure distributions (C
p
) at y/(b/2) = (a) 0.2;
(b) 0.65 (c) 0.95 of the ONERA M6 wing at M
∞
= 0.8395
and angle of attack α = 3.06
◦
. The CFD simulation results
are shown with a solid line (-). The wind tunnel experi-
mental data (from Schmitt, V. and F. Charpin (Schmitt and
Charpin, 1979)) is shown with square markers.
Transonic Wing Optimization by Variable-resolution Modeling and Space Mapping
493

maximizing lift case, so the objective function will
take the form of
H ( f (x)) = −C
L
, (3)
the design constraints denoted as
C ( f (x)) = [c
1
( f (x)) ,...,c
k
( f (x))]
T
. (4)
Maximizing lift will yield two nonlinear design
constraints for drag and area,
c
1
( f (x)) = C
D, f
(x) −C
D,max
≤ 0, (5)
c
2
( f (x)) = −A
f
(x) + A
min
≤ 0. (6)
where C
D,max
and A
min
are the maximum allowable
drag and minimum allowable cross-sectional area, re-
spectively.
3.2 Space Mapping Basics
Starting from an initial design x
(0)
, the generic space
mapping algorithm produces a sequence x
(i)
,i =
0,1... of approximate solutions to Eq. (1) as
x
(i+1)
= arg min
x
H
s
(i)
(x)
, (7)
where
s
(i)
(x) =
h
C
(i)
L,s
(x),C
(i)
D,s
(x),A
s
(x)
(i)
i
T
, (8)
is the surrogate model at iteration i. As previously
described, the accurate high-fidelity CFD model f is
accurate but computationally expensive. Using space
mapping, the surrogate s is a composition of the low-
fidelity CFD model c and a simple linear transforma-
tion to correct the low-fidelity model response (Ban-
dler et al., 2004). The corrected response is denoted
as s(x, p), where p represents a set of model parame-
ters and at iteration i the surrogate is
s
(i)
(x) = s(x, p). (9)
The SM parameters p are determined through a
parameter extraction (PE) process. In general, this
process is a nonlinear optimization problem where the
objective is to minimize the misalignment of surro-
gate response at some or all previous iteration high-
fidelity model data points (Bandler et al., 2004). The
PE optimization problem can be defined as
p
(i)
= arg min
p
i
∑
k=0
w
i,k
k f (x
(k)
) − s(x
(k)
,p)k
2
, (10)
where w
i,k
are weight factors that control how much
impact previous iterations affect the SM parameters.
Popular choices are
w
i,k
= 1 ∀i,k , (11)
and
w
i,k
=
1 k = i
0 otherwise
. (12)
In the first case, all previous SM iterations influence
the parameters; in the second case, the parameters de-
pend only on the most recent SM iteration.
3.3 Low-fidelity CFD Model
The low-fidelity model c is constructed in the same
way as the high-fidelity model f , but with a coarser
grid discretization and with a relaxed convergence cri-
teria - the so called variable-resolution modeling. Re-
ferring back to the grid study made in Section 2.5 and
inspecting Fig. 4(a), we make our selection for the
coarse low-fidelity model. Based on time and accu-
racy with respect of lift and drag, we select the grid
parameters that represent the second point from left,
giving a 107,054 elements. The time taken to eval-
uate the low-fidelity model is 13.2 minutes on four
Intel-i7-2600 processors in parallel. Inspecting fur-
ther the lift and drag convergence plot for the low-
fidelity model in Fig. 6, we note that the solution
has converged after 400-500 iterations. The maxi-
mum number of iterations for the low-fidelity model
is therefore set to 500 iterations. This reduces the
overall simulation time to 6.6 minutes. The ratio of
simulation times of the high- and low- fidelity model
in this case is high/low = 223/6.6 u 34. This is based
on the solver uses all 500 iterations in the low-fidelity
model to obtain a solution.
The low-fidelity CFD model c turns out to be very
noisy. In order to alleviate the problem, a second or-
der polynomial approximation model is constructed
(Koziel et al., 2011) using N
c
= 50 training points
sampled using latin hypercube sampling (LHS) (For-
rester and Keane, 2009) using the low-fidelity CFD
model. The polynomial approximation model is de-
fined as
c(x) = c
0
+ c
T
1
x + x
T
c
2
x, (13)
where c
1
= [c
1.1
c
1.2
c
1.3
]
T
and c
2
= [c
2.i j
]
i, j=1,2,3
.
The coefficients c
0
, c
1
, c
2
are found by solving a lin-
ear regression problem
c(x
k
) = c(x
k
), (14)
SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
494
100 200 300 400 500 600 700 800 900 1000
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
C
L
,10 x C
D
Iterations
C
L
10 x C
D
Figure 6: Lift and drag coefficient convergence plot for the
low-fidelity model obtained in the grid convergence study
using the ONERA M6 wing at Mach number M
∞
= 0.8395
and angle of attack α = 3.06
◦
.
where k = 1, . . .,N
c
. The resulting second order poly-
nomial model c has nice analytical properties, such as
smoothness and convexity.
3.4 Surrogate Model Construction
As mentioned above, the SM surrogate model s is
a composition of the low-fidelity CFD model c and
corrections or linear transformations where the model
parameters p are extracted using one of the PE pro-
cesses described above. The parameter extraction and
the surrogate optimization create a certain overhead
on the whole process and this overhead can be up to
80-90 % of the computational cost. This is due to the
fact that the physics-based low-fidelity models are in
general relatively expensive to evaluate compared to
the functional-based ones. Despite this, SM may be
beneficial (Zhu et al., 2007).
To alleviate this problem, the output SM with both
multiplicative and additive response correction is ex-
ploited here with the surrogate model parameters ex-
tracted analytically. We use the following formulation
s
(i)
(x) = A
(i)
◦ c(x) + D
(i)
+ q
(i)
(15)
or
s
(i)
(x) =
h
a
(i)
L
C
L,c
(x) + d
(i)
L
+ q
(i)
L
,
a
(i)
D
C
D,c
(x) + d
(i)
D
+ q
(i)
D
, A
c
(x)
i
T
,
(16)
where ◦ is a component-wise multiplication. No map-
ping is needed for the area A
c
(x) where, A
c
(x) =
A
f
(x) ∀x since low- and high-fidelity model repre-
sent the same geometry. Parameters A
(i)
and D
(i)
are
obtained using
h
A
(i)
,D
(i)
i
= argmin
A,D
i
∑
k=0
k f
x
(k)
− A ◦ c
x
(k)
+ Dk
2
,
(17)
where w
i,k
= 1, i.e., all the previous iteration points
are used to improve globally the response of the
low-fidelity model. The additive term q
(i)
is de-
fined such that is ensures a perfect match between the
surrogate and the high-fidelity model at design x
(i)
,
namely f
x
(i)
= s
x
(i)
or a zero-order consistency
(Alexandrov and Lewis, 2001). We can write the ad-
ditive term as
q
(i)
= f
x
(i)
−
h
A
(i)
◦ c(x
(i)
) + D
(i)
i
. (18)
Since analytical solution exists for A
(i)
,D
(i)
and
q
(i)
there is no need for non-linear optimization for
solving Eq. (10) to obtain the parameters. We can
obtain A
(i)
and D
(i)
by solving
"
a
(i)
L
d
(i)
L
#
=
C
T
L
C
L
−1
C
T
L
F
L
, (19)
"
a
(i)
D
d
(i)
D
#
=
C
T
D
C
D
−1
C
T
D
F
D
, (20)
where
C
L
=
C
L,c
(x
(0)
) C
L,c
(x
(1)
) ... C
L,c
(x
(i)
)
1 1 ... 1
T
,
(21)
F
L
=
C
L, f
(x
(0)
) C
L, f
(x
(1)
) ... C
L, f
(x
(i)
)
1 1 ... 1
T
,
(22)
C
D
=
C
D,c
(x
(0)
) C
D,c
(x
(1)
) ... C
D,c
(x
(i)
)
1 1 ... 1
T
,
(23)
F
D
=
C
D, f
(x
(0)
) C
D, f
(x
(1)
) ... C
D, f
(x
(i)
)
1 1 ... 1
T
,
(24)
which are the least-square optimal solutions to the lin-
ear regression problems
C
L
a
(i)
L
+ d
(i)
L
= F
L
, (25)
C
D
a
(i)
D
+ d
(i)
D
= F
D
. (26)
Note that C
T
L
C
L
and C
T
D
C
D
are non-singular for
i > 1 and assuming that x
(k)
6= x
(i)
for k 6= i. For i =
1 only the multiplicative SM correction with A
(i)
is
used.
Transonic Wing Optimization by Variable-resolution Modeling and Space Mapping
495

3.5 Optimization Algorithm
Here, we formulate the optimization algorithm ex-
ploiting the SM based surrogate and a trust-region
convergence safeguard (Forrester and Keane, 2009).
The trust-region parameter λ is updated after each it-
eration. This algorithm will be used in applications
presented in this thesis. The optimization algorithm
is as follows:
1. Set i = 0; Select λ, the trust region radius; Eval-
uate the high-fidelity model at the initial solution,
f (x
(0)
);
2. Using data from the low-fidelity model c, and f
at x
(k)
,k = 0, 1, . ..,i, setup the SM surrogate s
(i)
;
Perform PE;
3. Optimize s
(i)
to obtain x
(i+1)
;
4. Evaluate f (x
(i+1)
);
5. If H( f (x
(i+1)
)) < H( f (x
(i)
)), accept x
(i+1)
; Oth-
erwise set x
(i+1)
= x
(i)
;
6. Update λ;
7. Set i = i + 1;
8. If the termination condition is not satisfied, go to
2, else proceed;
9. End; Return x
(i)
as the optimum solution.
The termination condition is set to kx
(i)
− x
(i−1)
k <
10
−3
.
4 NUMERICAL EXAMPLES
In this section, we apply the proposed optimization
algorithm to the lift maximization of a rectangular
wing at transonic conditions. The direct solution
of the original problem in Eq. (1) has not been at-
tempted due to the heavy computational cost of the
high-fidelity model. We formulate the problem and
describe the setup. Then, we present the results of
numerical optimization.
4.1 Setup
The wing is unswept and untwisted and is constructed
by two NACA 4 digit airfoils, located at the root and
tip, as described in Fig. 1. The root airfoil is fixed
to be NACA 2412. The tip airfoil is to be designed.
The initial design x
(0)
for the wing tip is chosen at
random at the start of each optimization run. The
normalized semi-wingspan is set as twice the wing
chord length c as (b/2) = 2c. All other wing param-
eters are kept fixed. The design vector can be written
as x = [m, p,t/c]
T
, where the variables represent the
wing tip NACA 4 digit airfoil parameters.
The objective is to maximize the lift coefficient
C
L, f
subject to constraints on the drag coefficient
C
D, f
≤ C
D,max
= 0.03 and the wing tip normalized
cross-sectional area A ≥ A
min
= 0.01. The side con-
straints on the design variables are 0.02 ≤ m ≤ 0.03,
0.7 ≤ p ≤ 0.9 and 0.06 ≤ t/c ≤ 0.08.
4.2 Results
Two optimization runs were performed, denoted as
Run 1 and Run 2. The numerical results are given
in Table 1, and the initial and optimized airfoil cross-
sections are shown in Fig. 7(a) and Fig. 7(b), respec-
tively.
In Run 1, the lift is increased by +10% and the
drag is pushed above its constraint at C
D,max
= 0.03,
where the optimized drag coefficient is C
D
= 0.0311.
The drag constraint is violated slightly, or by +4%,
which is within the 5% constraint tolerance band. The
lift-to-drag ratio is decreased by -14%. The proposed
method requires less than 10 high-fidelity model eval-
uations, where 50 low-fidelity model evaluations are
used to create the approximation model and 8 high-
fidelity model evaluations for each design iteration. It
is evident that the optimized wing tip airfoil is thicker
as the normalized cross-sectional area is increased by
+26%, and the increased drag can be related to the in-
crement in area. No change is in the camber m, but
the location of the maximum camber p has moved
slightly aft.
The initial design for Run 2 violates the drag con-
straint. The proposed method is, however, able to
push the drag to its constraint limit where the opti-
mized drag coefficient is slightly violated, by +2%).
While the drag is decreased by -11%, the lift is main-
tained and only drops by -1%. As a result, the lift-
to-drag ratio is increased by +11%. The proposed
method requires less than 9 high-fidelity model eval-
uations (50 low-fidelity model evaluations used to
create the approximation model and 7 high-fidelity
model evaluations). The optimized wing tip airfoil is
thinner than the initial design (the normalized cross-
sectional area is reduced by -20%). Little changes are
made to the camber m and the maximum camber lo-
cation p.
Comparing runs 1 and 2, we note that although
starting from different initial designs the optimized
designs show similarities in two of three design vari-
ables, the maximum camber m and maximum camber
location p. The third, the airfoil thickness t/c differs
by approximately 2%. The shock on the mid wing has
been moved aft on both the upper and the lower sur-
SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
496

Table 1: Numerical comparison of Run 1 and Run 2, initial
and optimized designs. The ratio of the high-fidelity model
evaluation time to the low-fidelity is 34.
Initial Optimized
Variable Run 1 Run 2 Run 1 Run 2
m 0.0200 0.0259 0.0200 0.0232
p 0.7000 0.8531 0.8725 0.8550
t/c 0.0628 0.0750 0.0793 0.0600
C
L
0.2759 0.3426 0.3047 0.3388
C
D
0.0241 0.0344 0.0311 0.0307
C
L
/C
D
11.4481 9.9593 9.7974 11.0358
A 0.0422 0.0505 0.0534 0.0404
N
c
- - 50 50
N
f
- - 8 7
Total Cost - - < 10 < 9
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
−0.2
−0.15
−0.1
−0.05
0
0.05
0.1
0.15
0.2
x/c
z/c
Run 1 Initial
Run 2 Initial
(a) Initial.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
−0.2
−0.15
−0.1
−0.05
0
0.05
0.1
0.15
0.2
x/c
z/c
Run 1 Optimized
Run 2 Optimized
(b) Optimized.
Figure 7: A comparison of Run 1 and Run 2, initial and
optimized designs. (a) Initial design comparison, and (b)
Optimized comparison. Run 1 is shown with a solid lines
(–), and Run 2 with dashed lines (- -).
faces. Also, a second shock as formed near the tip on
the upper surface. This causes the drag rise, as well
as an increase in lift since the pressure distribution has
opened up, as can be seen from Fig. 8.
5 CONCLUSIONS
A robust and efficient aerodynamic design optimiza-
tion methodology for wings using high-fidelity CFD
models has been presented. Our approach exploits
a cheap surrogate model to obtain an approximate
optimum design of an expensive high-fidelity CFD
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
−1
−0.5
0
0.5
1
1.5
x/c
C
p
Inital
Optimized
Upper Surface
Lower Surface
(a) y/(b/2) = 0.2.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
−1
−0.5
0
0.5
1
1.5
x/c
C
p
Inital
Optimized
Upper Surface
Lower Surface
Shock
(b) y/(b/2) = 0.65.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
−1
−0.5
0
0.5
1
1.5
x/c
C
p
Inital
Optimized
Upper Surface
Lower Surface
Shock
(c) y/(b/2) = 0.95.
Figure 8: Pressure distributions of the initial and optimized
design of Run 1 at y/(b/2) = (a) 0.2, (b) 0.65, and (c) 0.95,
where M
∞
= 0.8395 and angle of attack α = 3.06
◦
. Initial
design is shown with a solid line (–) and the optimum design
with a dashed line (- -).
model. The surrogate model is constructed using
a corrected second-order polynomial approximation
model derived from low-fidelity CFD model data.
The correction is performed using the output space
Transonic Wing Optimization by Variable-resolution Modeling and Space Mapping
497

mapping technique. The space mapping correction is
applied both to the objectives and the constraints, en-
suring zero-order consistency and a perfect alignment
between the surrogate and the high-fidelity model. To
our knowledge, this is the first application of the space
mapping methodology used in conjunction with low-
fidelity approximation models in aerodynamic shape
optimization. The proposed approach performs well
and optimized designs are obtained using only a few
high-fidelity model evaluations.
ACKNOWLEDGEMENTS
This work was funded by The Icelandic Research
Fund for Graduate Students, grant ID: 110395-0061.
REFERENCES
Abbott, I. and Von Doenhoff, A. (1959). Theory of wing
sections: including a summary of airfoil data. Dover.
Alexandrov, N. and Lewis, R. (2001). An overview of first-
order model management for engineering optimiza-
tion. Optimization and Engineering, 2(4):413–430.
ANSYS (2010). ANSYS FLUENT Theory Guide. AN-
SYS, Southpointe 275 Thecnology Drive Canonburg
PA 15317, release 13.0 edition.
Bandler, J., Cheng, Q., Dakroury, S., Mohamed, A., Bakr,
M., Madsen, K., and Sondergaard, J. (2004). Space
mapping: the state of the art. Microwave Theory and
Techniques, IEEE Transactions on, 52(1):337–361.
Echeverria, D. and Hemker, P. (2005). Space mapping and
defect correction. Computational Methods in Applied
Mathematics, 5(2):107–136.
Forrester, A. and Keane, A. (2009). Recent advances in
surrogate-based optimization. Progress in Aerospace
Sciences, 45(1-3):50–79.
Haikin, S. (1998). Neural Networks: A Comprehensive
Foundation. Prentice Hall.
Journel, A. and Huijbregts, C. (1978). Mining geostatistics.
Academic press.
Koziel, S., Cheng, Q., and Bandler, J. (2008). Space map-
ping. Microwave Magazine, IEEE, 9(6):105–122.
Koziel, S., Ciaurri, D. E., and Leifsson, L. (2011).
Surrogate-based methods. In Computational opti-
mization and applications in engineering and indus-
try, volume 359. Springer.
Koziel, S. and Leifsson, L. (2012). Knowlegde-based air-
foil shape optimization using space mapping. In 30th
AIAA Applied Aerodynamics Conference.
Leifsson, L. and Koziel, S. (2011a). Airfoil shape opti-
mization using variable-fidelity modeling and shape-
preserving response prediction. In Comp. Opt., Meth-
ods and Algorithms, volume 356. Springer.
Leifsson, L. and Koziel, S. (2011b). Variable-fidelity aero-
dynamic shape optimization. In Comp. Opt., Methods
and Algorithms, volume 356. Springer.
Minsky, M. and Papert, S. (1969). Perceptrons: An intro-
duction to computational geometry. The MIT Press,
Cambridge, MA.
NASA (2008). Onera-m6-wing validation case. In
http://www.grc.nasa.gov.
O’Hagan, A. and Kingman, J. (1978). Curve fitting and
optimal design for prediction. Journal of the Royal
Statistical Society. Series B (Methodological).
Queipo, N., Haftka, R., Shyy, W., Goel, T., Vaidyanathan,
R., and Kevin Tucker, P. (2005). Surrogate-based anal-
ysis and optimization. Progress in Aerospace Sci-
ences, 41(1):1–28.
Raymer, D. (2006). Aircraft design: a conceptual approach.
American Institute of Aeronautics and Astronautics.
Robinson, T., Willcox, K., Eldred, M., and Haimes,
R. (2006). Multifidelity optimization for variable-
complexity design. In Proceedings of the 11th
AIAA/ISSMO Multidisciplinary Analysis and Opti-
mization Conference, Portsmouth, VA.
Schmitt, V. and Charpin, F. (1979). Pressure distributions
on the onera-m6-wing at transonic mach numbers. Ex-
perimental Data Base for Computer Program Assess-
ment, Report of the Fluid Dynamics Panel Working
Group 04, AGARD AR 138, May 1979.
Simpson, T., Poplinski, J., Koch, P., and Allen, J. (July
2001). Metamodels for computer-based engineering
design: survey and recommendations. Engineering
with computers, 17(2):129–150.
Smola, A. and Sch
¨
olkopf, B. (2004). A tutorial on sup-
port vector regression. Statistics and computing,
14(3):199–222.
Søndergaard, J. (2003). Optimization using surrogate mod-
els by the space mapping technique. PhD thesis, PhD.
Thesis, Technical University of Denmark, Informatics
and mathematical modelling.
Tannehill, J., Anderson, D., and Pletcher, R. (1997). Com-
putational fluid mechanics and heat transfer. Taylor
& Francis Group.
Wild, S., Regis, R., and Shoemaker, C. (2008). Orbit:
Optimization by radial basis function interpolation in
trust-regions. SIAM Journal on Scientific Computing,
30(6):3197–3219.
Zhu, J., Bandler, J., Nikolova, N., and Koziel, S. (2007).
Antenna optimization through space mapping. An-
tennas and Propagation, IEEE Transactions on,
55(3):651–658.
SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
498
