A Study on a Decision Support Model for Strategic Alliance in

Express Courier Service

Friska Natalia Ferdinand

, Ki Ho Chung

, Hyun Jeung Ko

and Chang Seong Ko

Dep.of Industrial Engineering, Pusan National University, Daehak-ro, Geumjeong-gu, Busan, 609 – 735, Korea

Dep. of Management Information Systems, Kyungsung University, Daeyeon-dong, Nam-gu, Busan, 608-736, Korea

Dep. of Logistics, Kunsan National University, 558 Unversity Avenue, Gunsan, Jeonbuk, 573-701, Korea

Dep. of Industrial & Management Engineering, Kyungsung University, Daeyeon-dong, Nam-gu, Busan, 608-736, Korea

Keywords: Strategic Alliance, Express Courier Service, Multi-Objective Programming, Genetic Algorithm.

Abstract: The market competition of express courier service has become severe so that an express delivery company

is consistently under pressure to operate its service network as efficient as possible. In this regard, the

strategic alliance among small and medium companies can be a useful way in order to maintain their

competitiveness. To cope with such challenges, this study proposes a decision support model to examine the

feasibility of merging under-utilized courier service centers and collaborating consolidation terminals with

strategic alliances among them. The proposed models can be formulated as multi-objective programming

models maximizing the minimum expected profit increase of each participating company. A solution

procedure based on the maxmin criterion is developed by using a genetic algorithm. The applicability and

efficiency of the proposed models is demonstrated through illustrative numerical examples.

1 INTRODUCTION

The market of express courier service in Korea has

been expanding 20% or higher annually, which is

much faster increase than in other industry areas. It

however becomes already saturated because a large

number of companies are entering into the Korea

market. As a result, they are facing with high

competition with respect to low margin and high

quality of customer service (Chung et al., 2011).

Therefore, to cope with these substantial competition

pressures, strategic alliance is proposed as an

effective solution to the challenges faced by small

and medium sized enterprises in express courier

service. In this paper, the network design models

with strategic alliance are proposed to improve the

efficiency of the logistics networks among small and

medium express courier service companies. An

express courier network generally consists of

customer zones, service centers, and consolidation

terminals. The proposed model adopts a win-win

alliance relationship for the participating companies,

and suggests how to increase the net profit of each

company by harnessing their low demand and under-

utilized service centers, and sharing consolidation

terminals with available processing capacities. In

order to do this, a multi objective programming

model and the solution procedure was developed

based on genetic algorithm approach and coded in

matlab 7.0 with numerical examples in this study.

There have been a few of researches on the topic

of strategic alliances in logistics. Some researchers,

such as Chopra and Meindl (2004), Min (1996), and

Simchi-Levi et al. (2003), pointed out that the

companies which owned and operated their facilities

independently may benefit from the strategic

alliance scheme which is conceptually similar to

facility sharing. And optimal capacity allocation as a

solution methodology for dealing with facility

sharing was proposed by Cachon and Lariviere

(1999). With respect to the cutoff time adjustments

in an express courier network design, a couple of

researches have been conducted (Ko et al., 2010);

(Ko et al., 2011).

In particular, a study related to the express

courier service network design reflecting strategic

alliance was performed by Chung et al. (2009), and

they proposed a network design model for strategic

alliances among express courier service companies

by monopoly of service centers. And then, Chung et

al. (2010) extended their previous study to the

problem of sharing service centers where an integer

620

Ferdinand F., Chung K., Ko H. and Ko C..

A Study on a Decision Support Model for Strategic Alliance in Express Courier Service.

DOI: 10.5220/0004164406200625

In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (OMDM-2012), pages 620-625

ISBN: 978-989-8565-22-8

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

programming model and its solution procedure

based on a fuzzy set theoretic approach were

developed, and their study was performed under the

assumption that only service centers selected as

candidates for strategic alliance are considered.

Later, Chung at al. (2011) proposed a nonlinear

integer programming model for strategic alliance for

the survival of multiple service centers and a fuzzy

set theoretic solution procedure is used. And,

Ferdinand et al. (2012) extended Chung et al.

(2011)’s work by applying a genetic algorithm

method in order to consider the efficient operations

of consolidation terminals with respect to strategic

alliance. They proposed a decision making model

which dealt with closing/opening multiple service

centers and sharing consolidation terminals

simultaneously.

Therefore, this study extends Ferdinand et

al.(2012)’s work by considering the closing of

consolidation terminals, but taking the survival of

only single service center into account for strategic

alliance. In detail, it is first carried out that only a

single service center can survive in each merging

region, and then the opened service centers are

assigned to single or multiple consolidation

terminals within their capacity limitations.

2 PROBLEM DEFINITION

This paper is one of the extension works based on

the previous studies by Chung et al. (2009, 2010,

2011) and Ferdinand et al. (2012) so that the

problem situation is similar to the ones described in

their studies but some additional factors are taken to

account. In a courier service network of a company

in Korea, there are some service centers where the

daily pick-up demands are very low. In particular,

the regions that have low volume shipments in

service centers are called as Type I indicating the

potential merging regions, and the other service

centers do not belong to any merging regions called

as Type II. In general, small and medium sized-

enterprises (SMEs) are operating some under-

utilized service centers in Type I, achieving only for

customer satisfaction not generating profits. As such,

the concept of strategic alliance between SMEs can

be applied to the regions, Type I, for not only

reducing the operation costs of under-utilized

facilities without hurting their current service levels

but also increasing their net profits. The strategic

alliance works such a way that they participate to

collaborate in pick-up operations at the open service

centers in Type I as well as to share the capacities of

consolidation terminals by reassigning all the service

centers to the appropriate terminals. The

assumptions are as follows:

a) Within a merging area, only single service center

can be opened and all the other service centers are

closed after the alliance.

b) All pick-up amounts of closed service centers

within the same merging area are assigned to the

opened service centers after the alliance.

c) At least one terminal for each company must be

opened and the remaining is closed within a region

after the alliance.

d) The open Type I service centers in each merging

area as well as Type II service centers should be

reassigned to partnering companies’ available

consolidation terminals within the capacity

limitations.

Based on the setting, this paper proposes a non-

linear integer programming model which is designed

to maximize the minimum expected profit increase

of each participating company. The objective

function for the strategic alliance problem is maxmin

criterion, and genetic algorithm is developed to

solve the model. The mathematical formulation can

be described as follows:

Max

(1)

s.t.

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

AStudyonaDecisionSupportModelforStrategicAllianceinExpressCourierService

621

Table 1: The rules for opening/closing service centers.

Open Service Center Reallocated Pick-up Amount

Cases SC1 SC2 SC3 SC4 SC 1 SC 2 SC 3 SC 4

1 ○ SC2+SC3+SC4

2 ○ SC1+SC3+SC4

3 ○ SC1+SC2+SC4

4 ○ SC1+SC2+SC3

3 ALGORITHM DEVELOPMENT

The proposed solution algorithm in this study is

designed based on the work by Ferdinand et al.

(2012), in which they used integer based genetic

algorithm so that the parameters used in this study

are similar. In detail, this study develops six steps to

solve the proposed model based on the genetic

algorithm where it firstly chooses which service

centers (only single service center is opened) will be

opened/closed in each merging area, and then, in the

second step, assigns all the daily pick-up amounts to

the opened Type I service centers. The third step

decides which consolidation terminals are opened or

closed for the allocation of shipments from service

centers, and then reallocates all of service centers to

the available consolidation terminals. Finally, it

calculates the profits of each company based on

maxmin criterion. In the proposed genetic algorithm,

four genetic operators are used such as cloning,

parent selection, crossover, and mutation operators.

The parameter values for genetic algorithm are: the

population size equals to 500; the maximum number

of generations is 150; the cloning rate is set at 2%;

the crossover rate and mutation rate are 60-70% and

4-7%, respectively.

3.1 Chromosome Design

In this study, we consider four companies for

strategic alliance for which the chromosome consists

of four parts dealing with decision variables shown

in Figure 1. The first through third parts are

designed for Type I where five regions of each

company are considered, and the last part is for Type

II where ten regions are considered in each company.

In addition, each company are currently running two

consolidation terminals. In the first part, the first to

the fifth genes describe which service center will be

opened in each merging region where one service

center is allowed to be opened according on the rule

in Table 1.

The values of five genes, considering that single

service center is opened in each merging region, can

be selected from 1 to 4 based on the available cases

shown in Table 1 since there four companies. For

example, Figure 1 shows that the first five genes

have integer values such as 1, 3, 2, 4 and 1 which

means, in region 1 through region 5, company 1’s

service center is opened (SC1), while in region 2, 3,

and 4, the opened service centers are company 3’s,

company 2’s, and company’s 4 (SC3, SC2, and SC4)

respectively.

Figure 1: Chromosome representation.

The second part in Figure 1 describes which

consolidation terminals will be opened in each

region where single or two terminals are allowed to

be opened according to the rule in Table 2. The

value of five genes can be selected from 1 to 3 based

on the available cases. Case 1 and Case 2 show only

single terminal is opened, while, in Case 3, two

consolidation terminals are opened.

In Figure 1, the values of sixth through ninth

gens are randomly generated, in which the genes

have values such as 3, 1, 2, and 1. This means that

two terminals (Terminal 1 and 2) are opened in

Company 1, while in Company 2, 3, and 4 only one

terminal (Terminal 3, 6, and 7) are opened

respectively based on Table 2. The third and fourth

parts in Figure 1 show that the allocations of service

centers to consolidation terminals for the merging

and non-merging regions.

3.2 Crossover and Mutation Operators

This study applied a three-point crossover where the

first point is used to assign which service centers can

be opened; the second point is used to assign which

consolidation terminals will be available; the last

point is used for reassigning the Type I and Type II

service centers to the opened consolidation

terminals. The crossover process can be seen in

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

622

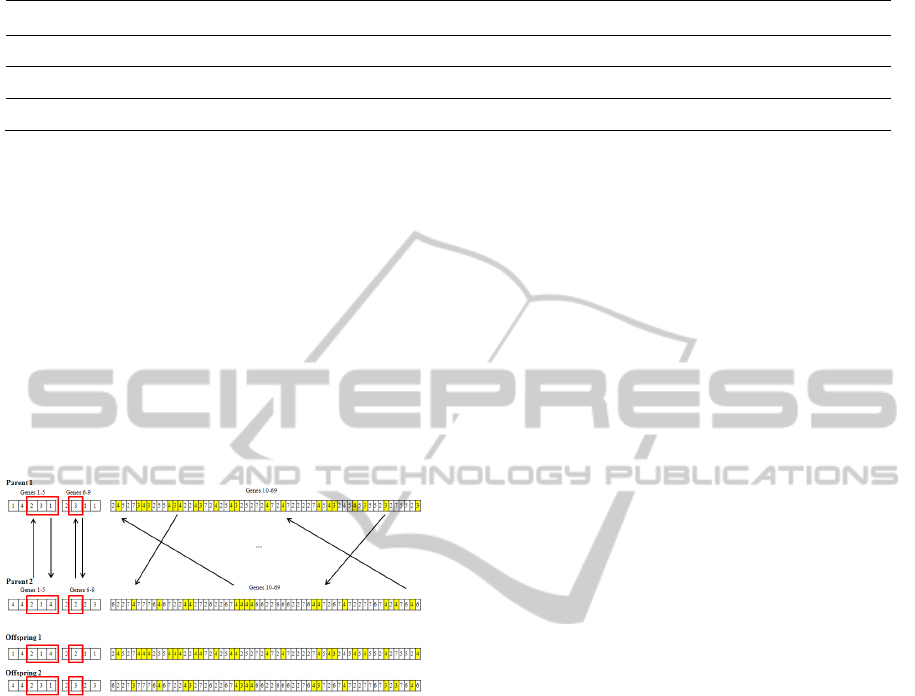
Table 2: The rules for opening/closing terminals.

Case Company 1’s Opened Terminal Company 2’s Opened Terminal Company 3’s Opened Terminal Company 4’s Opened Terminal

1 1 3 5 7

2 2 4 6 8

3 1 & 2 3 & 4 5 & 6 7 & 8

Figure 2.

For the first point, the general method that many

people already adopt is used. However, in the

second and third point, a different way should be

applied. For example, the gene 7 of parent 1, the

value is three, which means two the available

terminals are 3 and 4 in the company, while in

parent 2, the value is two, meaning that only

terminal 4 is available. As such, if a usual crossover

is directly used, it will cause some errors because the

numbers of available terminals are different.

Therefore, this process needs some restrictions to get

the possibility of searching a wider solution space.

Figure 2: Crossover method.

As mentioned before, the mutation process also

has some restrictions where not all of the genes can

be flipped by randomly. In particular, the sixth until

ninth genes will not have mutation process because

there is a dependency with the tenth until sixty-ninth

genes, dealing with which terminals will be

available. For avoiding the errors, the first step is to

select the six genes with random, where two genes

will be randomly selected from the section of service

centers, and the other four genes are selected from

the parts of merging and non-merging terminal

allocation areas. In doing so, the procedure is

divided it into three parts, the first part is from the

first until fifth genes; the second part is from the

tenth to twenty-eighth genes; the third part is from

the tenth to sixty ninth genes. In the second and third

parts, all of the genes depend on the distances

between the terminals and the service centers. In this

regard, the mutation performs one of the following

actions:

a) If both terminals are available based on distance

rules for merging region and non-merging region,

then they switch positions in the solution.

b) If both terminals are not available in distance,

then they are not changed randomly but it takes a

specially designed process.

4 NUMERICAL EXAMPLE

For the numerical example, there are four express

courier service companies where each company has

two consolidation terminals with the different fixed

costs for all terminals in Table 3. The set of the

consolidation terminals of Company 1 is {1, 2}; the

set of Company 2 is {3, 4}; the set of Company 3 is

{5, 6}. The set of Company 4 is {7, 8}. Every

opened service center of each company should be

allocated to a consolidation terminal. The daily pick-

up amount for each Type I service center is

determined in the range between 10 and 50 units

while for each Type II between 100 and 500 units

through random-number generation. In addition,

service center closedown results in the reduction of

daily fixed cost for maintaining and operating the

service centers, so these cost reductions should be

converted into net profit value. These are obtained

by generating random-number between $50 and

$100 per day. Terminal capacity is equally assigned

to 3,500 units for the consolidation terminals of the

four companies.

In this scenario, all the terminals will not be

available for each company within the region

because of the terminal distance. The assumptions

for this scenario are as follows:

a) The consolidation terminal is available for its

company

b) If the other company’s terminal distance is more

than 70 km then it will be not available in that

region.

The overall procedures are coded in Matlab 7.0 and

all the results are shown in the Figure 3. The optimal

solution for maxmin criterion can be obtained using

GA, and the result after GA implementation is

AStudyonaDecisionSupportModelforStrategicAllianceinExpressCourierService

623

Table 3: Fixed operating costs of terminals for each company.

Company 1 Company2 Company 3 Company 4

1 2 3 4 5 6 7 8

1672 1896 1337 1021 1714 1905 1483 1259

shown in Table 4(a) and 4(b). Only in the merging

region 1, Company 1’s service center is selected to

be open while in the region 3 and 4, company 4’s

service center is selected and company 2’s service

center is selected in regions 2 and 5 respectively.

The available terminals in this case are terminal 2, 3,

4, 6, and 7. Based on maxmin criterion, the total

profit of $134,567 represents the total sum of the

profit for each company, where the profits for each

company are $34,459, $26,128, $28,862, and

$45,119 respectively.

Table 4: The summary of test result.

a) Available Terminals for Each Company

Company Available Terminal

1 2

2 3 & 4

3 6

4 7

b) Type I Service Centers

Merging Region

Opened Service

Center

Terminal

Allocation

1 1 2

2 2 3

3 4 6

4 4 7

5 2 3

c) Type II Service Centers

Non-Merging

Region

Terminal Allocation

C1 C2 C3 C4

1 2 6 6 2

2 7 7 2 7

3 6 7 3 3

4 4 3 6 6

5 2 2 2 6

6 6 3 6 2

7 2 6 6 2

8 2 3 4 2

9 6 3 6 6

10 2 3 7 7

5 CONCLUSIONS

This study developed a decision making model for

strategic alliance among express courier companies

Figure 3: The outputs by GA implementation.

by using GA and its efficient solution procedure

which aimed to maximize the expected profit from

express courier services by merging the service

centers. It also determined whether the existing

consolidation terminals were still opened or not in

Type I and Type II regions. The solution procedure

was developed using GA and coded in Matlab 7.0.

As a result, the model and solution procedure

enabled express courier companies to earn

maximized profit by merging the service centers and

also by reducing the number of consolidation

terminals.

ACKNOWLEDGEMENTS

This research was supported by BASIC Science

Research Program through the National Research

Foundation of Korea(NRF) funded by the Ministry

of Education, Science Technology (2011-0027218).

REFERENCES

Cachon, G. P. and Lariviere, M. A., (1999). Capacity

choice and allocation: strategic behavior and supply

chain performance, Management Science, vol.45, no.8,

pp. 1091-1108.

Chopra, S. and Meindl, P., (2004). Supply chain

management: strategy, planning and operation, NJ:

Pearson Prentice Hall.

Chung, K. H., Ko, C. S., Hwang, Y. M., and Rho, J. J.,

(2010). “Network design for strategies alliance in

express courier services: a fuzzy set approach”,

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

624

International Journal of Innovative Computing,

Information and Control, vol.9, no.1, pp.349-359.

Chung, K. H., Ko, H. J., Ferdinand, F. N. and Ko, C. S.,

(2011). “A fuzzy set-theoretic approach to the weak

strategic alliance for the survival of multiple service

center in express courier services, ICIC Express

Letters: International Journal of Research and

Surveys, vol.5, no.2, pp.385-389.

Chung, K. H., Rho, J. J., and Ko, C. S., (2009). “Strategic

alliance model with regional monopoly of service

centers in express courier services”, International

Journal of Service and Operation Management, vol.5,

no.6, pp.774-786.

Ferdinand, F. N., Chung, K. H., Ko, H. J. and Ko, C. S.,

(2012). "Genetic algorithm-based approach to multi-

objective decision making model for strategic

alliances in express courier services", ICIC Express

Letters, vol.6, no.4, pp.929-934.

Ko, C. S., Yoon, E. M., Chung, K. H. and Ko, H. J.,

(2011). "Strategic partnership-based reconfiguration of

express package service network with extension of

consolidation terminal capacity", ICIC Express

Letters, vol.5, no.2, pp. 373-378.

Ko, H. J., Lee, H. J., and Ko, C. S., (2011). "A Study on

the Design of Express Courier Service Network Based

on the Cut-off Time Adjustments", International

Journal of Innovative Computing, Information and

Control, vol.9, no.1, pp.335-347.

Min, H., (1996). Consolidation terminal location-

allocation and consolidated routing problems, Journal

of Business Logistics, vol.17, no.2, pp.235-263.

Simchi-Levi, D., Kaminsky, P., and Simchi-Levi, E.,

(2003). Designing and managing the supply chain:

concepts, strategies, and case studies, McGraw-Hill.

AStudyonaDecisionSupportModelforStrategicAllianceinExpressCourierService

625