
Simulating Vaccination Control and Herd Immunity Threshold in
EcoDemics
Yasaman Majdabadi Farahani and Robin Gras
University of Windsor, School of Computer Science, Windsor, Ontario, Canada
Keywords: Agent-based Epidemiology, Herd Immunity, Vaccination, Ecosystem Simulation.
Abstract: Modeling infectious diseases and exploring immunization interventions has been a major concern for the
last century. Deadly pandemics transmitted from animals to humans such as SARS, rabies, H1N1 and the
lack of extensive parameters in most of the epidemic simulations, imposes a great importance on simulating
realistic ecosystems to study different aspects of epidemics and mitigation strategies. To this end,
EcoDemics was built upon EcoSim to model epidemics in an evolutionary ecosystem simulation. Due to the
high mitigation capacity and significance of the immunization intervention, we explore vaccination
techniques with various time delays and population proportions. Based on the herd immunity theory, the
whole population can be protected against a contagious disease by vaccination of a fraction of individuals.
We investigate this principle in EcoDemics and compare our results with real epidemics data.
1 INTRODUCTION
Infectious pandemic diseases transmitted from
animals to humans (zoonotic infections) such as
SARS, rabies, and H1N1 have had a deadly effect
throughout the world. Although the final number of
infections, illnesses, and deaths could vary
tremendously depending on the pandemic and other
multiple factors, it is certain that without adequate
planning and preparations, a pandemic in the 21st
century has the potential to cause enough illnesses to
overwhelm public health system at all levels.
During the last few decades, several models have
been developed to explore mitigation strategies in
the disease models. Tsunoda, et al. simulated the
spread of influenza for exploring the most efficient
mass vaccination strategies to prevent an epidemic
(Tsunoda et al., 2011). In another study, the role of
travel restrictions in delaying and ending the H1N1
pandemic has been explored (Bajardi et al., 2011). A
large-scale epidemic simulation was used in
(Ferguson et al., 2006) to examine intervention
options in an influenza outbreak. Keeling, et al.
modeled vaccination strategies against foot-and-
mouth disease (Keeling et al., 2003). The roles of
individual imitation behavior and population
structure in vaccination were explored in (Fu et al.,
2010) to control infectious diseases. In these models,
however, many details of the progression of
infection and individual behaviors are neglected.
Additionally, either unrealistic mixed-populations
have been assumed or the number of different
subpopulation types is small.
On the hand, network analysis has been used as
an explanatory tool to describe the evolution and
spread of epidemics (Eubank et al., 2004), (Keeling
and Eames, 2005), and (Meyers et al., 2005).
Pourbohloul, et al. used contact network
epidemiology to predict several control policies for a
mildly contagious disease (Pourbohloul et al., 2005).
However, all network-based simulations are limited
by the fact that there is no simple way to ascertain
the sensitivity of the epidemiological results to the
details of the network structure. Other challenges
also concern data collection, modeling dynamics in
network connections and dealing with complexity of
the models. A recent example of this problem exists
in the spatial network model presented in (Kim et
al., 2011) which focuses on the disease spread from
the central point of a static vertices graph and fails to
model the dynamics of the network structure.
This imposes a great importance on simulating
realistic ecosystems to study the spread of diseases
and control strategies. There are a number of
evolutionary artificial life ecosystems, the most
notable ones are Tierra (Ray, 1991), Avida (Adami,
1998), Echo (Harber, 1995), PolyWorld (Yaeger,
1993), Framsticks (FRAMSTICKS), and EcoSim
(Gras et al., 2009). Among them, to our knowledge,
280
Majdabadi Farahani Y. and Gras R..
Simulating Vaccination Control and Herd Immunity Threshold in EcoDemics.
DOI: 10.5220/0004165202800288
In Proceedings of the 2nd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2012),
pages 280-288
ISBN: 978-989-8565-20-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

the only one that integrated some notions of diseases
diffusion is EcoSim. EcoDemics (Majdabadi
Farahani et al., submitted) is built upon EcoSim to
allow the study of the spread of an epidemic
associated with mitigation strategies. EcoSim was
first introduced and developed by Gras, et al. This
powerful complex ecosystem simulation tries to gain
knowledge about natural ecosystems by simulating
intelligent adaptive agents interacting and evolving
in a large and dynamic environment. The novelty of
modeling disease in EcoDemics comes from the fact
that each agent has a behavioral model which
evolves during the simulation. Unlike classic disease
models which assume a well-mixed static population
or a uniform population with random movements,
EcoDemics is based on a dynamic population with
respect to both the number of births and deaths, as
well as the migration of the individuals. These
dynamic properties that affect the disease spread and
mitigation strategy are emergent from the behavioral
model of the agents.
The previously built framework gave us a rich
ground, with more depth and details to study
different epidemic outbreaks along with different
strategies that control the spread. Due to the high
mitigation capacity and significance of the
immunization intervention in the literature of
epidemiology, we explore vaccination technique
with various scenarios in this paper. The rest of the
paper is organized as follows. The next section is
dedicated to a brief description of the EcoSim. We
next present the disease model used in EcoDemics,
followed by the vaccination and herd immunity
explanation. The experiments and results will be
discussed afterwards. We then conclude our work
and discuss our future plans in the conclusion
section.
2 AGENTS, BEHAVIOUR, AND
ENVIRONMENT IN ECOSIM
The individuals (or agents) of this simulation are
prey or predators acting in a simulated environment.
Individuals act in a dynamic environment composed
of 1000×1000 cells. Each cell may contain several
individuals and some amount of food. Each
individual possesses several physical characteristics
such as: age, minimum age for breeding, speed,
vision distance, possibility of disease, immunity,
levels of energy, and amount of energy transmitted
to the offspring. Energy is provided to individuals by
the resources (food) they find in their environment.
Prey consume grass, which is dynamic in quantity
and location, whereas predators hunt prey
individuals. An individual consumes some energy
each time it performs an action. Each individual
performs one unique action during a time step, based
on its perception of the environment. Each agent
possesses a Fuzzy Cognitive Map (FCM) to compute
the next action (Kosko, 1986). In each FCM, three
kinds of concepts are defined: sensitive (such as
distance to foe or food, amount of energy, etc.),
internal (fear, hunger, curiosity, satisfaction, etc.),
and motor (evasion, socialization, exploration,
breeding, etc.). The FCM of an individual, which
also represents its genome, is transmitted to its
offspring after being combined with the mate’s
genome and after the possible addition of some
mutations. The behavior model of each individual is
therefore unique.
For the study of disease we focus on patterns of
epidemic outbreaks in prey as they have higher
populations. The possible actions for prey are:
1. Evasion, which is in the opposite direction of the
barycenter of the five closest predators within the
prey’s range of vision. The new position of the prey
is computed using the speed of the prey.
2. Search for food, which is toward the closest food
(grass) within the prey’s range of vision.
3. Socialization, which is the direction toward the
closest possible mate within the prey’s range of
vision.
4. Exploration, in which the individual moves at its
speed in a random direction.
5. Resting, in which nothing happens.
6. Eating, which includes a change in the cell grass
amount and also in the individual’s energy and
hunger levels.
7. Breeding: If the energy levels of two individuals
in a same cell are more than a certain threshold, their
two genomes are similar, and their both choices of
action are breeding, then mating will occur.
The detailed explanations regarding individuals
FCM and associated concepts along with the values
for the initial parameters and actions can be found in
(Gras et al., 2009).
Our simulation iterates through a loop such that
every execution of the loop represents a single time
step in which every individual makes a decision and
performs an action. The parameters of the
environment are updated at the end of each time
step.
SimulatingVaccinationControlandHerdImmunityThresholdinEcoDemics
281

3 D
I
V
A
E
C
EcoDe
m
modifie
d
model
o
strength
with a
p
modelin
g
birth, de
system
u
review
b
Figure 1:
within h
o
The
and not
p
rovide
s
for spec
i
individu
a
world.
T
small w
i
and pre
y
p
InitInfectio
b
ecome
I
SEASE
M
A
CCINAT
C
ODEMI
C
m
ics (Farahan
i
d
Suscepti
b
o
f transmiss
i
is based on
p
redato
r
-
p
rey
g
, genome
r
ath, and evol
u
u
nique and m
o
b
riefly the dis
e
The disease
m
o
st disease prog
r
disease start
s
from the be
g
s
the system
w
i
es to group
t
a
ls are mostl
y
T
he initial loc
a
i
ndow having
y
are infecte
d
n
. Individua
l
infected ba
s
M
ODEL A
N
ION IN
C
S
i
et al., sub
m
b
le-Infected-
R
i
on disease.
modeling a
n
interaction.
r
epresentatio
n
u
tion are all
p
o
re realistic.
I
e
ase model us
m
odel represen
t
r
ession.
s
in a user s
p
g
inning of th
e
w
ith a chanc
e
t
ogether, as a
t
y
uniformly
a
tion of the i
n
1/256 of the
d
according
t
l
s subjected
s
ed on a pr
o
N
D
m
itted) appli
e
R
emoved (
S
The EcoDe
m
n
atural ecosy
s
Individual b
a
n
, and mod
e
p
oints makin
g
I
n this sectio
n
ed in EcoDe
m
t
ing different
s
p
ecified time
e
simulation.
T
e
to stabilize
t
initializatio
n
d
istributed i
n
n
fec
t
ion is set
size of the
w
t
o the
p
roba
b
to the dis
o
bability fun
c
e
s a
S
IR)
m
ics
s
tem
ased
e
ling
g
our
n
we
m
ics.
s
tates
step
This
and
n
the
n
the
in a
w
orl
d
b
ility
s
ease
c
tion
p
re
ind
i
inf
e
p
ro
b
set
to
c
cer
t
acc
Ta
b
thei
p
oth
e
adj
a
co
m
sa
m
fro
m
dis
t
eac
ste
p
to
b
int
r
W
h
inf
e
ind
i
nu
m
inf
e
a
Mi
d
an
d
inf
e
on
the
(m
i
epi
d
rec
o
ad
d
a
r
s
ented later
i
viduals then
e
cted and
b
abilities pre
a minimum t
i
c
arry the dis
e
t
ain individu
a
ording to the
p
b
le 1: Probabil
r description.
Name
p
InitInfection
Pr
o
w
p
immune
Pr
o
p
heal
P
p
kill
Pr
o
Infected ind
i
e
r individual
s
a
cent cells.
T
m
es from the
f
m
e species t
e
m
the same
t
ributed in t
h
h
other (Asp
i
p
, the uninfe
c
b
e infecte
d
b
r
oduced in (1)
=
0,
11exp
h
ere
is th
e
e
cted with th
e
i
viduals in th
e
m
ber of infect
e
The values o
e
ction. We d
e
a
ccording to
d
dle-aged ind
i
d
ol
d
-aged in
d
e
cted.
At each time
the paramete
r
minimum
i
nInfected). T
h
d
emic, whic
h
o
vered indi
v
d
ition, individ
u
r
esult of the
in equation
enter differe
n
then recov
e
sented in Ta
b
i
me (minInfe
c
e
ase before it
a
ls are give
n
p
aramete
r
p
im
m
i
ties of the di
D
e
o
bability of initi
a
w
ith the disease,
w
si
m
o
bability of the i
n
th
e
P
robability of re
c
o
bability that des
c
would kill th
e
i
viduals can
s
in the same
T
he interactio
n
f
act that indiv
i
e
nd to group
prey speci
e
h
e world but
i
nal, and Gra
s
c
ted individu
a
b
ased on a
p
:
21
e
probability
disease, s is
t
e
same cell a
s
e
d individual
s
f
and ar
e
e
fine two dif
fe
the age gro
i
viduals are a
t
d
ividuals are
a
step some in
d
r
p
heal
, given
time to
h
is model is
b
h
is characte
r
iduals will
u
als would b
e
disease bas
e
n
(1). The
n
t
SIR disea
s
e
red based
b
le 1. In ad
d
c
ted) for the
i
t
is able to h
e
n
immunity t
o
mune
.
i
sease model
a
e
scription
a
lly infecting an
i
w
hich happens o
n
m
ulation.
n
dividual being i
m
e
disease.
c
overing from in
f
cribes an option
a
e
infected indivi
d
spread the
d
cell and the
n between i
n
v
iduals belong
togethe
r
: i
n
e
s are not
r
are spatially
s
, 2010). At
e
a
ls have the
p
p
robability f
u
=
,
of individu
a
the number o
s
i, and r repr
e
s
in the adjac
e
e
the paramet
e
f
erent values
f
o
up of the i
n
t
low risk, w
h
a
t greater ris
k
d
ividuals reco
that they ha
v
carry the
based on the
r
ized by the
b
ecome im
m
e
subjected t
o
ed on p
kill
.
infected
s
e stages;
on the
d
ition, we
ndividual
e
al. Also,
o
disease
a
long with
ndividual
n
ce in the
m
mune to
f
ection.
a
l step that
d
ual.
d
isease to
8 closest
n
dividuals
ing to the
n
dividuals
r
andomly
close to
e
ach time
p
ossibility
u
nction p
i
=
0
0
(1)
l i being
f
infected
e
sents the
e
nt cells.
e
rs of the
f
o
r
and
n
dividual.
h
ile young
k
of being
v
e
r
based
v
e passed
disease
SIR-type
fact that
m
une. In
o
death as
Figure 1
SIMULTECH2012-2ndInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
282

represents different states of disease progression.
The role of the predator-prey interaction and the
significance of the behavioral model of each
individual in forming the population, as well as its
consequence on spreading the infection, have been
highlighted in EcoDemics (Majdabadi Farahani, et
al., submitted). Including a behavioural model to the
population and the spatial distribution of the
individuals in the environment, have led to a novel
disease model that has shown reasonable
concordance with real wildlife epidemics. Since the
ultimate goal in any epidemiological modeling is to
study possible control strategies that help mitigate
the spread of diseases, three different control
techniques have been implemented in the
EcoDemics: vaccination, pharmaceutical
interventions, and quarantine. The fact that
vaccination control strategy has shown the highest
mitigation rate among the three tested, has motivated
us to further explore immunization control and
verify the existence of the herd immunity threshold.
We would like to see if the implementations
regarding vaccination strategies lead to results
conform to the ones observed in wildlife epidemics
to confirm the interest of our approach for more in
deep epidemiological studies.
3.1 Vaccination and Herd Immunity
Threshold
We assume no initial immunity to the infection for
individuals in the general disease model and full
immunity for those susceptible individuals being
vaccinated.
3.1.1 Variation in Time Delay
As intervention timing has had a great interest in
many disease mitigation studies including
mathematical (Garner et al., 2011), (Kelso et al.,
2009) and real-data epidemic simulations (Ferguson
et al., 2006), we explore the effect of immunization
delay in the first experiment. We apply the
vaccination with various time delays from the
initiation of the infection and observe the difference
in the magnitude of infection.
3.1.2 Variation in Proportion of Population
In another experiment we study the effect of
vaccinating various population percentages. In this
case, vaccination starts immediately after the
initiation of the disease and is performed in 3
different phases. Each phase consists of 3 steps in
which the number of vaccinated individuals are the
same. In the first phase, the number of vaccinated
individuals in each step is high to accelerate the
mitigation process. We call this number Vaccination
Capacity (VC). In the second and third phase, the
number of vaccinated individuals in each step
decreased to 2/3 and 1/3 of VC, respectively.
Therefore, to ascertain the immunization of the
chosen total percentage, VP, of the population
during the whole 3 phases of vaccination, maximum
vaccination capacity is defined as follows:
=∗/6
Where VC is maximum vaccination capacity in a
step, VP is total vaccination percentage of the
population and S is the number of susceptible
agents. This process guaranties that the total number
of individuals vaccinated during the 9 steps that
cover the 3 phases is equal to VP * S.
3.1.3 Herd Immunity
There is an important theory in epidemiology known
as herd immunity which proposes that, all the
individuals can be protected against a contagious
disease by vaccination of a fraction of a population
(John and Samuel, 2000). The proportion of
vaccinated individuals in a population above which a
contagious disease eradicates is the herd immunity
threshold. This value depends on the type of the
infection and population parameters, such as
individual interactions and spatial distribution (Fine,
1993). We are interested to investigate this principle
in EcoDemics. This will be explored by varying the
VP value and observe the epidemic trend over time
in the next section.
4 RESULTS
The simulation is implemented in C++ and all
experiments are performed on Sharcnet
(SHARCNET) using the Linux XC cluster. At the
beginning stage of the simulation, the prey and
predator populations are set to 12000 and 500
respectively. The life span of an individual is from 1
to maxAge, where maxAge is computed randomly
for each individual to be centred around 46.
Initiation of the infection occurs after the
stabilization stage that is, after 750 time steps of the
simulation. At this stage of the simulation run, the
prey and predator populations grow to 178340 and
29656 respectively. Due to the large number of
parameters in our EcoDemics, numerous scenarios
can be defined and experimented on. Different range
of values for the disease parameters along with their
SimulatingVaccinationControlandHerdImmunityThresholdinEcoDemics
283
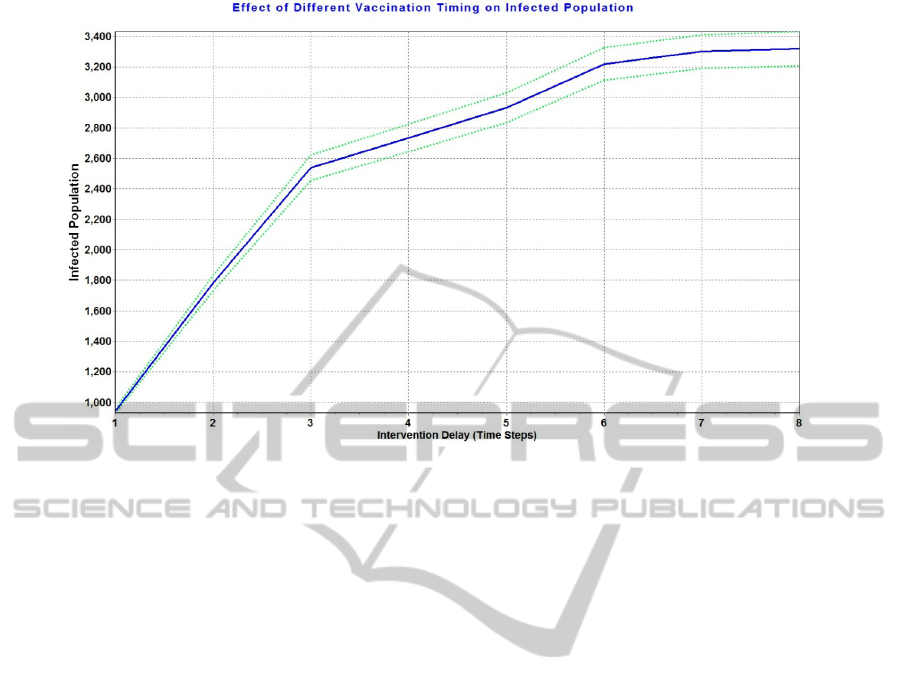
Figure 2: Effect of varying the vaccination delay on the number of infections. Dotted lines represent one standard deviation.
principal effect on the epidemic have been studied in
EcoDemics (Farahani et al., submitted). For this
experiment we chose one set of parameters but many
such sets have been tested and led to the same
results.Using probability of p
InitInfection
= 0.05, only
5% of the susceptible prey in the initial window are
set to be infected during the initial infection stage.
The infected individual goes through different states
based on the parameters and probabilities of the
disease model. We define the general infection
model with the following specifications: susceptible
individuals become infected with the disease based
on the probability function (1) with = -0.2 and =
2 for high risk individuals, and = -0.15 and = 4
for low risk individuals, infected individuals may
recover from the disease after a minimum of 10 time
steps (minInfected) and with the probability (p
heal
) of
60% and the recovered individual is naturally
immune. The killing rate of 1% is also assigned to
this infection model according to p
kill
.
4.1 Variation in Time Delay
In order to study the effect of timing in vaccination,
we applied various time delays to the vaccination
from the initiation of the infection, and then observe
the corresponding values of the total number of
infections. We vaccinated 90% of the population in
delays ranging from 1 to 8 time steps after the
initiation of the infection. We computed the average
of 10 different independent runs of the simulation.
Our results show that with the early initiation of the
vaccination, which correspond to an intervention
delay of 1, the number of infections would be
around 900, 5% of the population; however, having
an intervention delay of 3, would increase the
number of infections to 2500, 14% of the
population. In other words, a delay of only 2 time
steps in the application of the vaccination increases
the magnitude of infection in the population by a
factor of 2.7 (Figure 2). This result follows the
process of the studies presented in (Kelso, et al.
2009), in which final attack rates in a worst case
epidemic increased by a factor of 3.2 between the
intervention delays of 1 and 3 time steps.
4.2 Variation in Percentage of
Population Vaccinated
To study the importance of the quantity of the
vaccination, different proportions of the population
are vaccinated. For this purpose, the value of VP is
varied from 10% to 90% of the population. The
average numbers of infected individuals and
epidemic duration for 10 runs using the same VC
value are computed. Figure 3 shows the effect of
different vaccination rates on the total infected
population.
Similarly, Figure 4 shows the effect of different
vaccination rates on the total duration of the
infection. These results are similar to other
vaccination models such as (Keeling et al., 2003),
which used the 2001 real cattle epidemic as a
template (see the appendix). As shown in the Figure
3, the infection has a maximum value of almost
SIMULTECH2012-2ndInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
284

Figure 3: Effect of varying the number of vaccinated individuals on total infected population. The total number of
vaccinated individuals is in abscissa and the cumulative total number of infected individual during the whole epidemic
duration is in ordinate. Highest and lowest values in infected population correspond to the lowest (10%) and highest (90%)
VP values respectively. Dotted lines represent one standard deviation.
355,000 individuals, which is a cumulative value
over more than 100 time steps, while the number of
vaccinated individuals is around 10,000, which
represents approximately 10% of the population.
However, the number of infections decreases
drastically to less than 10,000 agents when the
number of vaccinated individuals is more than 60%
of the population and even decreases to 2000
infections when 90% of the population is vaccinated.
The comparison of actual infections with the study
that used a real cattle epidemic (Keeling et al., 2003)
is not applicable, as it considered the number of
infected farms instead of the infected population;
however, the obtained curves have exactly the same
trend: the average size of epidemic declines rapidly
with the vaccination rate at each time step, reaching
a lower plateau that corresponds to a disease
eradication threshold (Keeling et al., 2003).
In Figure 4, it can be seen that the epidemic lasts
for a period of 466 time steps with 10% vaccination;
however, the duration is substantially reduced to less
than 22 time steps while the vaccination percentage
is more than 70% of the population. Similarly, this
trend matches the reactive vaccination for cattle
(Keeling et al., 2003) which started with 400 days
for the lowest vaccination rate, versus 466 time steps
in our study, and achieved the herd immunity
threshold in around 25 days, versus 22 time steps in
our study.
Figure 5 depicts epidemic curves for different
VP values. The curves with the highest and lowest
peak represent the VP values of 10% and 90%
respectively, and each curve is the average for 10
independent runs. Only the first 50 time steps of the
infection are depicted, as they are the most
characteristic part of the epidemic patterns. For the
VP of 60%, 70%, 80% and 90%, which are the four
lowest curves, the epidemic was significantly
mitigated and finally eradicated. For the lower VP
values, although the trend of the epidemic over the
first 15 time steps is similar to the 4 aforementioned
curves, the vaccination strategy was unable to fully
suppress the infection at the desired time and we
observed jumps of infection after the global decline.
This phenomenon suggests an immunity threshold to
ensure the eradication of the epidemic over an
acceptable duration. For this study the vaccination
percentage of the total population needs to be equal
or above a threshold of 60% to stop the disease
diffusion. In qualitative context, this result is
validated by the study about the herd immunity: high
levels of herd immunity in cattle can prevent the
long tail of the epidemic and is necessary to inhibit
stochastic jumps of infection for a given special
transmission kernel (Keeling et al., 2003). This
correspondence only applies to the threshold for
eradication of infection by vaccination: lower levels
of vaccination can generate complex, nonlinear,
spatio-temporal disease dynamics (Keeling et al.,
2003). As mentioned earlier, we observed this
SimulatingVaccinationControlandHerdImmunityThresholdinEcoDemics
285

Figure 4: Effect of varying the number of vaccinated individuals on the infection duration. The total number of vaccinated
individuals is in abscissa and the duration of the epidemic is in ordinate. Highest and lowest values in epidemic duration
correspond to the lowest (10%) and highest (90%) VP values respectively. Dotted lines represent one standard deviation.
nonlinear complex behaviour in lower VP values
that are unable to eradicate the disease.
The above results show that our system, which
includes much more complex mechanisms than the
others, like the ability to model concepts such as
complex individual behaviours, multi-level food
chains, reproduction, evolution or speciation,
produces results similar to the ones observed in
systems dedicated to epidemic modeling. This is a
significant result for the evaluation of EcoDemics’
potential as a platform for studying open complex
problems in epidemiology that are unable to be
tackled in simpler simulations.
5 CONCLUSIONS
We simulated vaccination strategies in EcoDemics
to model the mitigation of epidemics. We explored
the effect of this technique with various timing and
population percentage parameters. Our experiments
revealed that there is a threshold value for the
parameter setting the percentage of the population
that is vaccinated. This is the same result observed
in the herd immunity study: lower levels of
vaccination can generate complex, nonlinear, spatio-
temporal disease dynamics (Keeling et al., 2003).
We observed that with a value greater than 60%, the
pattern of the disease spread changes abruptly.
However, these measures may not be appropriate to
apply directly as quantitative values, as extensive
disease specific parameters need to be adjusted
depending on the different situations (Harvey et al.,
2007); (Keeling et al., 2003); (Holland, 1995).
Nevertheless, this study highlighted the importance
of effective vaccination policies in mitigating the
infection and confirms the fundamental role of
increasing individual’s immunity over a relatively
wide area to inhibit stochastic jumps of infection
(Keeling et al., 2003).
We have shown that the results obtained with our
simulation are in reasonable concordance with the
ones already obtained with other studies. The
interest of our approach is that we do not design a
system dedicated to disease spread modeling.
Our system is based on a large scale evolving
ecosystem simulation which has already proved its
interest for the study of complex ecological
problems such as community composition (Devaurs
and Gras, 2010) or speciation mechanisms (Aspinal
and Gras, 2010).
The proof that our system can easily integrate
disease models and generate realistic data of disease
spread for various mitigation strategies is essential to
give us the opportunity to study other situations that
cannot be described with a simpler system. Indeed,
EcoDemics can easily be extended to tackle
numerous difficult open problems.
We are currently studying the precise effect of
predators in prey infections, with the assumption
that infected preys are more vulnerable to predation.
This help us to analyze different scenarios in an
SIMULTECH2012-2ndInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
286
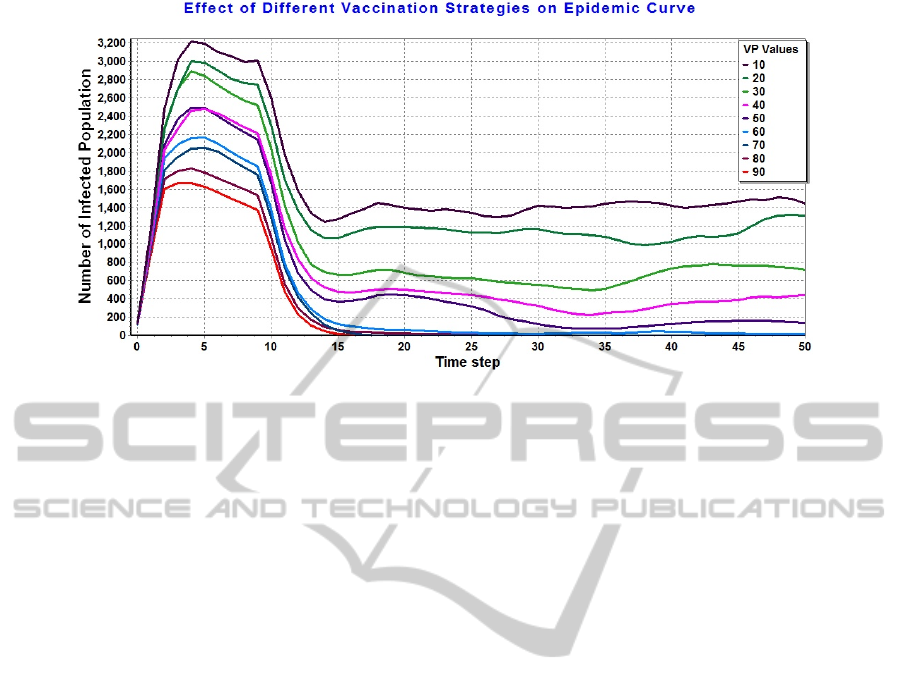
Figure 5: Effect of varying the number of vaccinated population on epidemic curve. Each curve is the average of 10
independent runs for the corresponding VP value.
ecosystem; for instance if the infection can be
eradicated by the predators, or if predator removal
can increase the incidence of parasitic infection.
As the individuals in our system search for mates
and breed, sexually transmitted diseases can easily
be integrated. This will allow for studying the
specific properties of sexually transmitted disease in
large multi-species populations.
The way a disease impacts the genome through
the course of evolution is also an interesting
question to investigate. Several biological and
ecological studies have tried to argue these types of
impacts in the evolution of individuals and the
necessity of their recognition and interpretation for
both public health (Gluckman and Hanson, 2005)
and the population of the ecosystem (Bar-David,
2006). As our system integrates the notions of
genome, transmission of genome and evolution, we
will have the ability to analyze how individuals try
to adapt and overcome a disease spread through
evolution. Co-evolution of diseases and hosts could
also be represented. We will be able to track and
analyze the way that one affects the other and
influences its evolution over long time periods.
ACKNOWLEDGEMENTS
This work is supported by the NSERC grant
ORGPIN 341854, the CRC grant 950-2-3617 and
the CFI grant 203617 and is made possible by the
facilities of the Shared Hierarchical Academic
Research Computing Network (SHARCNET).
REFERENCES
Adami, C., 1998. Introduction to Artificial Life. Springer,
New York.
Aspinal, A., Gras, R., 2010. K-Means Clustering as a
Speciation Method within an Individual-Based
Evolving Predator-Prey Ecosystem Simulation.
Active Media Technology, Lecture Notes in
Computer Science, pages 318-329, Toronto.
Bajardi, P., Poletto, C., Ramasco, Jose J., Tizzonil, M.,
Colizza, V., Vespignani., A., 2011. Human Mobility
Networks, Travel Restrictions, and the Global Spread
of 2009 H1N1 Pandemic. PLOS ONE, 6(1): e16591.
Bar-David, SH., Lloyd-Smith, J. & Getz, W. M., 2006.
Dynamics and Management of Infectious Disease in
Colonizing Populations. Ecology, 87(5):1215–1224.
Devaurs, D. & Gras., R., 2010. Species abundance
patterns in an ecosystem simulation studied through
Fisher‟s logseries. Simulation Modelling Practice
and Theory, 18(1):100 – 123.
Eubank, S., Guclu, H., Kumar, V. S. A., Marathe, M. V.,
Srinivasan, A., Toroczkai, Z. & Wang, N., 2004.
Modelling disease outbreaks in realistic urban social
networks. Nature, 429:180–184.
FRAMSTICKS: www.framsticks.com
Ferguson, N. M., Cummings, D. A. T., Fraser, C., Cajka,
J. C., Cooley, P. C., & Burke, D. S., 2006. Strategies
for mitigating an influenza pandemic. Nature,
442:448–452.
Fine P. E., 1993. Herd immunity: history, theory, practice.
Epidemiologic Reviews.; 15(2):265–302.
Fu, F., Rosenbloom, D. I., Wang, L., Nowa, K. M. A.,
2010. Imitation dynamics of vaccination behaviour
on social networks. The Royal Society ,B 278 (1702):
42–49.
Garner, M. G., Cowled, B., East, I. J., Moloney, B. J.
Kung, N. Y., 2011. Evaluating the effectiveness of
early vaccination in the control and eradication of
equine influenza—A modelling approach. Preventive
Veterinary Medicine, 99(1):15-27.
Gluckman, P. D., Hanson, M. A., Spencer, H. G., 2005.
Predictive adaptive responses and human evolution.
SimulatingVaccinationControlandHerdImmunityThresholdinEcoDemics
287

TRENDS in Ecology and Evolution, 20:527-533.
Gras, R., Devaurs, D., Wozniak, A., & Aspinall, A., 2009.
An Individual-based Evolving Predator-Prey
Ecosystem Simulation using Fuzzy Cognitive Map
as Behavior Model. Journal of Artificial
Life,15(4):423-463.
Hraber, P.T., Jones, T., & Forrest, S., 1997. The ecology
of echo. Artificial Life 3. 165–190.
Harvey, N., Reeves, A., Schoenbaum, M., Zagmutt-
Vergara, F., Dub_e, C., Hill, A., Corso, B., McNab,
W., Cartwright, C., & Salman, M., 2007. The North
American Animal Disease Spread Model: A
simulation model to assist decision making in
evaluating animal disease incursions. Preventive
Veterinary Medicine, 82:176-197.
Holland, J. H., 1995. Hidden order: How adaptation
builds complexity. Addison-Wesley, Reading.
John, T. J., Samuel, R., 2000), Herd immunity and herd
effect: new insights and definitions. Eur J Epidemiol.
16(7):601–606.
Keeling, M. J., Woolhouse, M. E. J., May, R. M., Davies,
G. & Grenfellk, B. T., 2003. Modelling vaccination
strategies against foot-and-mouth disease, Nature,
42: 9.
Keeling, M. J., & Eames, K. T., 2005. Networks and
epidemic models. Journal of the Royal Society,
Interface, 2(4):295–307.
Kelso, J. K, Milne, G. J., Kelly, H., 2009. Simulation
suggests that rapid activation of social distancing can
arrest epidemic development due to a novel strain of
influenza, BMC Public Health, 117(9).
Kim, T., Li, K., Zhang, A., Sen, S., & Ramanathan, M.,
2011. A Computational Model of Mitigating Disease
Spread in Spatial Networks. International Journal of
Artificial Life Research (IJALR), 2(2):77-94.
Kosko, B., 1986), Fuzzy cognitive maps. International
Journal of Man-Machine Studies, 24(1):65 – 75.
Majdabadi Farahani, Y., Khater, M., and Gras, R.
(submitted). EcoDemics: Modeling Epidemic Spread
in a Simulated Predator-Prey Evolutionary
Ecosystem. To appear in the Journal of Artificial
Life.
Meyers, L. A., Pourbohloul, B., Newman, M. E. J.,
Skowronski, D. M. & Brunham, R. C., 2005.
Network theory and SARS: predicting outbreak
diversity. Journal of Theoretical Biology, 232(1):71–
81.
Pourbohloul, B., Meyers, L. A., Skowronski, D. M.,
Krajden, M., Patrick, D., Brunham, R. C.,, 2005.
Modeling control strategies of respiratory pathogens.
Emerging Infectious Diseases, 11:1249-1256.
Ray, T., 1991. An approach to the synthesis of life.
Artificial Life II, 6:371-408.
SHARCNET: www.sharcnet.ca
Tsunoda, K., Shinya, K., SuzukiInvestigation, Y., 2011)
Investigation of efficient protection from an
influenza pandemic using CARMS. Artificial Life
and Robotic. 16:1-4.
Yaeger, L., 1993. Computational genetics, physiology,
metabolism, neural systems, learning, vision, and
behavior or polyworld. Life in a new context.
Artificial Life III, 17:263-298.
APPENDIX
Figure 6 shows how an epidemic can be controlled
by the rapid vaccination of cattle during the early
stages, using the 2001 epidemic of Great Britain as a
template. Throughout, vaccination is of cattle only
and assumed to be at 90% efficacy. Expected
number of farms reporting infection against the
number of cattle vaccinated per day (bottom axis) or
the corresponding time to achieve the disease
eradication threshold of around 5.5 million cattle
(top axis). Solid and dashed lines show the result
when different culling is performed. Solid lines
depict the average size of the simulated epidemic,
which declines rapidly with daily vaccination rate,
reaching a lower plateau at a rate of around 300,000
cattle per day. This rate corresponds to achieving the
deterministic vaccination threshold in around 25
days. Similarly, Figure 7 represents the expected
duration of the epidemic by varying the number of
vaccinated cattle (Keeling et al., 2003).
Figure 6: Effect of varying the number of vaccinated cattle
on total infected population using the 2001epidemic of
Great Britain as a template (Keeling et al., 2003).
Figure 7: Effect of varying the number of vaccinated cattle
on the epidemic duration using the 2001epidemic of Great
Britain as a template (Keeling et al., 2003).
SIMULTECH2012-2ndInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
288
