Single Input Single Output Time Series Artificial Neural Network

Models for Free Residual Chlorine Forecasting in Water Distribution

Networks

Selcuk Soyupak

, Hurevren Kilic

, Ibrahim Ethem Karadirek

and Habib Muhammetoglu

Civil Engineering Dept., KTO Karatay University,

Akabe Mah. Alaaddin Kap Cad. No:130, 42020, Karatay, Konya, Turkey

Department of Computer Engineering, Gediz University, Seyrek Kampusu, 35665, Menemen, Izmir, Turkey

Environmental Engineering Department, Akdeniz University, Dumlupinar Bulvari, 07058, Kampus, Antalya, Turkey

Keywords: Single Input Single Output Artificial Neural Networks, Time Series, Water Distribution Networks.

Abstract: The aim of this study is to investigate the utilization of Single Input Single Output Time Series Artificial

Neural Networks models as a forecasting tool for estimating Free Residual Chlorine levels at critical

locations of fairly complex Water Distribution Systems. The response surface methodology was adopted in

identifying performance and precision trends as a function of number of steps used as inputs and number of

steps ahead to predict (Horizons). The utilized response surfaces were for coefficient of determination and

mean absolute error. The creation of response surfaces was achieved by developing Artificial Neural

Network models for several combinations of number of steps used as inputs and number of steps ahead to

predict that enable the calculations of coefficient of determination and mean absolute error for the selected

combinations. Then these results have been assembled to obtain contour maps by distance weighted least

square technique. The maximum attained coefficient of determination levels were within the range 0.656 to

0.974, while minimum achievable mean absolute error levels were within the range 0.0080 to 0.0284 ppm.

The achieved mean absolute error is very low when compared with the followings: a) the applied Free

Residual Chlorine levels from the source which is about 0.5 ppm and b) the minimum detection limit of the

chlorine analyzers given as 0.01 ppm.

1 INTRODUCTION

Data driven artificial intelligence techniques provide

alternative solutions to deterministic approaches for

controlling and providing acceptable levels of Free

Residual Chlorine (FRC) levels in Water

Distribution Systems (WDSs). The reason for

shifting to data driven approaches from deterministic

approaches lies in the following facts: i) decay

kinetics of chlorine within water is nonlinear and it

is very complex to formulate while it is being

transported to consumption points (Gibbs et al.,

2003; May et al., 2004; Bowden et al., 2006; May et

al., 2008), ii) because of the mentioned complexity,

the dynamics of decay kinetics are usually

oversimplified by modelers to obtain solutions, that

reduce predictive powers of deterministic models

and consequently guarantees only low levels of

precision. One additional weakness of deterministic

models is the problem of unnecessary computational

efforts even for small WDSs (Polycarpou et al.,

2002). Finally, a major drawback of deterministic

models lies in the difficulties of accurately

predicting the future water demands as emphasized

by (May et al., 2008).

Milestone research within this field goes back to

the beginning of last decade (Rodriguez and

Serodes, 1999; Serodes et al., 2001). The data

requirement of Artificial Neural Network (ANN)

approach by these investigators includes the past

records of FRC levels at critical points, and at

chlorine dosing and application locations. They also

needed the past records of variables at dosing points

that were expected to influence chlorine decay in

WDSs. The literature indicates adoption of a variety

of data driven approaches under different application

conditions. A control oriented model using ANN

methodology has been developed and compared

with autoregressive moving average (ARMA)

588

Soyupak S., Kilic H., Karadirek I. and Muhammetoglu H..

Single Input Single Output Time Series Artiﬁcial Neural Network Models for Free Residual Chlorine Forecasting in Water Distribution Networks.

DOI: 10.5220/0004171105880593

In Proceedings of the 4th International Joint Conference on Computational Intelligence (NCTA-2012), pages 588-593

ISBN: 978-989-8565-33-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

approaches as forecasters; ANN gave better results

(May et al., 2004). A multi-layer perceptron (MLP)

ANN with back-propagation has been developed by

selecting the inputs required with adoption of three

different techniques (Gibbs et al., 2003, Sharma,

2000). The MLP model performed better than

traditional linear regression (Gibbs et al., 2003).

Further MLP ANN was indicated to be implemented

as an online tool to aid in the determination of

chlorine levels (Gibbs et al., 2003). A general

regression neural network (GRNN) model for

forecasting FRC levels within a WDS has also been

developed (Bowden et al., 2006). The GRNN model

was shown to perform better than a multiple linear

regression (MLR) model as a forecaster. Some

investigators have emphasized the importance of the

Input Variable Selection (IVS) for modeling and

forecasting the residual chlorine dynamics within

WDSs (Serodes et al., 2001; Gibbs et al., 2006). In

recent years, some progress has been achieved as

related to solving IVS problem. Wrapping and

filtering are two basic classes of approaches to IVS

problem (May et al. 2008 b). The wrapping

methodology as a search process has the objective of

obtaining best performance of the calibrated model

(Serodes et al., 2001). Filtering methodology is a

model-free approach where linear correlation

coefficient and mutual information have been

proposed as two measures of dependence for input

variable selection (Sharma, 2000; May et al. 2008

b). A recent study has shown that multiple input

ANN models with high predictive power and

precision can be developed for WDSs supplied with

high quality waters; however, these models can be

utilized only for forecasting purposes. The study has

further questioned the applicability and validity of

multiple input ANN models as control instruments

for FRC levels for systems similar in nature to the

system investigated within the scope of this earlier

work (TUBITAK, 2009).

In this particular research, we have investigated

the possibility of developing Single Input Single

Output Time Series Artificial Neural Networks

(SISO-TS-ANN) that utilize appropriate Number of

Steps Used As Inputs (NSUAI) and number of steps

ahead to predict (H), so that the developed models

can be utilized as an efficient and economical

forecasting instrument. The question of selecting

appropriate NSUAI and appropriate number of H

has been answered by utilizing response surfaces for

coefficient of determination (R

) and Mean Absolute

Error (MAE). The coefficient of determination (R

)

and mean absolute error (MAE) are commonly

utilized statistical entities for judging model validity

or quality of fit (StatSoft’s STATISTICA Electronic

Statistics Textbook, 2012). R

values are calculated

using model predictions and measurements as

variables. In order to realize the goals of the

research, a WDS operated by ASAT (Antalya Water

and Wastewater Administration, Turkey) has been

selected as pilot. The following sections first present

the properties of the studied WDS and monitoring

program, as a summary. Secondly, the details of the

adopted SISO-TS-ANN modeling approach and the

adopted response surface methodology are given.

The methodology gives general guidelines to select

the best location specific NSUAI and H

combinations for models with high predictive power

and precision. Finally, results are presented and

discussed in detail.

2 METHOD

2.1 Antalya Konyaalti WDS

The SISO-TSS-ANN models have been developed

for Antalya Konyaalti Water Distribution System

(KWDS) operated by ASAT, as depicted in Figure

1. The pilot network is one of the major sub-

networks of Antalya water supply system. The area

that being served by KWDS has the following

properties: i) It can be operated independently, ii)

The area has supervisory control and data

acquisition system (SCADA) infrastructure, iii) The

WDS is relatively new. The raw water source is

groundwater which is pumped to the network after

chlorination at Bogacay Pumping Station and

Reservoir. Chlorination is not applied at any other

location within KWDS. There is one balancing

reservoir and eight monitoring stations operated with

the existing SCADA system to collect on-line data

to achieve the goals of this specific research.

Figure 1: Map showing KWDS and Antalya WDS with

monitoring stations, reservoirs and pumping station.

SingleInputSingleOutputTimeSeriesArtificialNeuralNetworkModelsforFreeResidualChlorineForecastinginWater

DistributionNetworks

589

The established monitoring stations can collect on-

line water quality data sets for FRC, temperature

(T), electrical conductivity (EC), pH and turbidity

(Turb). Pressure (P) and water flow rates (Q) are

also being recorded on-line and continuously for the

monitoring stations: Bogacay Pumping Station and

Reservoir, ON 67, ON 68, ON 70, ON 71, ON 72,

ON 73 , ON 74 and Hurma Balancing Reservoir

(Figure 1). These parameters are expected to

influence FRC levels and its decay kinetics in WDS.

Data sets from the analyzers were recorded and

stored at five-minute intervals at SCADA center. For

this study, these data sets were converted into

quarterly averaged values. We have utilized the

water quality and operational data provided by

ASAT for the months September 2009 and October

2009 for the above mentioned monitoring stations.

There was some missing data within time series for

some of the parameters due to short time power

failures and due to unavoidable operational

problems. Missing data points were generated

synthetically by averaging the earlier and following

values. The number of missing information was

relatively few.

2.2 Selection of Input Variables

The purpose of ANN modeling in WDS field of

water resources engineering is in general to obtain a

mathematical tool to calculate the necessary input

levels at control points to satisfy the desired levels of

chlorine in future at the critical points of WDS. In

this study, the control point is Bogacay Pumping

Station and Reservoir and the critical points are the

other monitoring stations namely ON 67, ON 68,

ON 70, ON 71, ON 72, ON 73, ON 74 and Hurma

Balancing Reservoir (Figure 1). An earlier study

(TUBITAK, 2009) has suggested that in cases where

supplied water quality is high and where the chlorine

decay rates are very low, tools other than classical

ANN methodology with multiple inputs should be

investigated and adopted for more simplified

modeling. Because of this observation, in this

research only single controllable input, namely Free

Residual Chlorine at Bogacay Pumping Station and

Reservoir (FRC

Bogacay

), has been utilized. Further,

the collection of data for model building has been

realized in such a way that the specifically created

FRC perturbations within control point has created

FRC time series at monitoring points that are

suitable to develop SISO-TS-ANN models for

control purposes as consistent with (TUBITAK,

2009).

2.3 Model Building

Through this research we wanted to investigate the

applicability of SISO-TS-ANN models developed as

a FRC control tool and as a forecaster for a fairly

complex WDS with high quality raw water input.

The selected single input was FRC

Bogacay

. In order to

initiate ANN modeling one has to decide about

selecting NSUAI and H. In order to establish criteria

to select the best combinations of NSUAI and H for

different monitoring stations, we have adopted

response surface methodology for R

and MAE. The

creation of response surfaces required selection of

experimental matrix that covers reasonable and

practical combinations of (NSUAI,H), including

(8,2), (8,4), (8,8), (12,2), (12,4), (12,8), (24,2),

(24,4), (24,8), (48,2), (48,4), (48,8), (72,2), (72,4),

(72,8), (96,2), (96,4), (96,8). The tested NSUAI

values were 8, 12, 24, 48, 72 and 96. The tested H

values were 2, 4 and 8. The R

and MAE values have

been estimated for each combination of NSUAI and

H; then the contour plots were prepared by using

STATISTICA (SANN, 2008). SISO-TS-ANN

models for forecasting FRC levels at monitoring

stations have been developed utilizing the software

SANN ANS (Statistica Automated Neural Network-

Automated Network Search) package (SANN,

2008). Modeling constraints were as follows: 1)

Minimum and maximum numbers of hidden neurons

were 3 and 11 respectively, 2) 20 candidate

structures have been tested for each data set and only

the one with best performance and precision was

requested to be retained. MLP approach has been

instructed to be utilized.

The best SISO-TS- ANN for each monitoring

station has been found by examining the response

surfaces developed for that station. Several different

combinations of types of hidden and output

activation functions, number of neurons, number of

steps used as inputs (NSUAI) and number of steps

ahead to predict (H) have been tested and the one

that minimizes MAE and maximizes R

has been

selected and listed in Table 1.

3 RESULTS AND DISCUSSIONS

The developed response surfaces as contour plots for

and MAE are given in Figures 2 and 3

respectively. These figures cover response surfaces

for monitoring stations ON69, ON71 and Hurma

balancing reservoir only. Similar response surfaces

are obtained for other monitoring stations as well. In

order to save space, only the response surfaces of

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

590

> 0.94

< 0.94

< 0.92

< 0.9

< 0.88

< 0.86

< 0.84

< 0.82

< 0.8

0 102030405060708090100

NSUAI

(a) ON-69

> 0.98

< 0.98

< 0.96

< 0.94

< 0.92

< 0.9

< 0.88

< 0.86

0 102030405060708090100

NSUAI

(b) ON-71

> 0.85

< 0.83

< 0.78

< 0.73

< 0.68

< 0.63

< 0.58

< 0.53

< 0.48

0 102030405060708090100

NSUAI

Figure 2: Contour plots for R

against number of steps

used as inputs (NSUAI) and number of steps ahead to

predict (horizons).

three stations are presented here. If we examine the

response surfaces for different stations, the

following strategies for selecting NSUAI and H

combinations can be reached:

1) The suggested NSUAI and H levels for

monitoring station ON69: The dynamics of

KWDS

dictate to utilize as much past data as

> 0.032

< 0.032

< 0.03

< 0.028

< 0.026

< 0.024

< 0.022

< 0.02

< 0.018

< 0.016

0 102030405060708090100

NSUAI

(a) ON-69

> 0.02

< 0.02

< 0.018

< 0.016

< 0.014

< 0.012

< 0.01

< 0.008

< 0.006

0 102030405060708090100

NSUAI

(b) ON-71

> 0.036

< 0.034

< 0.03

< 0.026

< 0.022

< 0.018

0 102030405060708090100

NSUAI

Figure 3: Contour plots for MAE against number of steps

used as inputs (NSUAI) and number of steps ahead to

predict H (horizons).

possible for this station; however the forecasting

horizon should be kept about 4 to 6 (1 to 1.5

hours) so that maximum R2 and minimum MAE

values can be attained (Please refer Figures 2-a

and 3-a).

2) The suggested NSUAI and H levels for

monitoring station ON71: The general trend is to

SingleInputSingleOutputTimeSeriesArtificialNeuralNetworkModelsforFreeResidualChlorineForecastinginWater

DistributionNetworks

591

utilize as many past data as possible for this

station since Figure 2-b indicates that as NSUAI

reaches to 96 (= 1 day) , R

values is about 96 %.

The same trend is also obvious from Figure 3-b

that indicates the reduction and minimization of

MAE as NSUAI increases. Both Figures 2-b and

3-b indicate to keep forecasting horizon either

lowest or highest for the studied range.

3) The suggested NSUAI and H levels for

monitoring station Hurma Balancing Reservoir:

The general trend suggests the utilization of as

many past data as possible for this station since

Figure 2-c indicates that as NSUAI reaches to 96

(= 1 day) , R

values is more than 85 %. Figure

3-c indicates the reduction and minimization of

MAE as NSUAI increases. Figure 3-c further

suggests keeping forecasting horizon as large as

possible to minimize MAE.

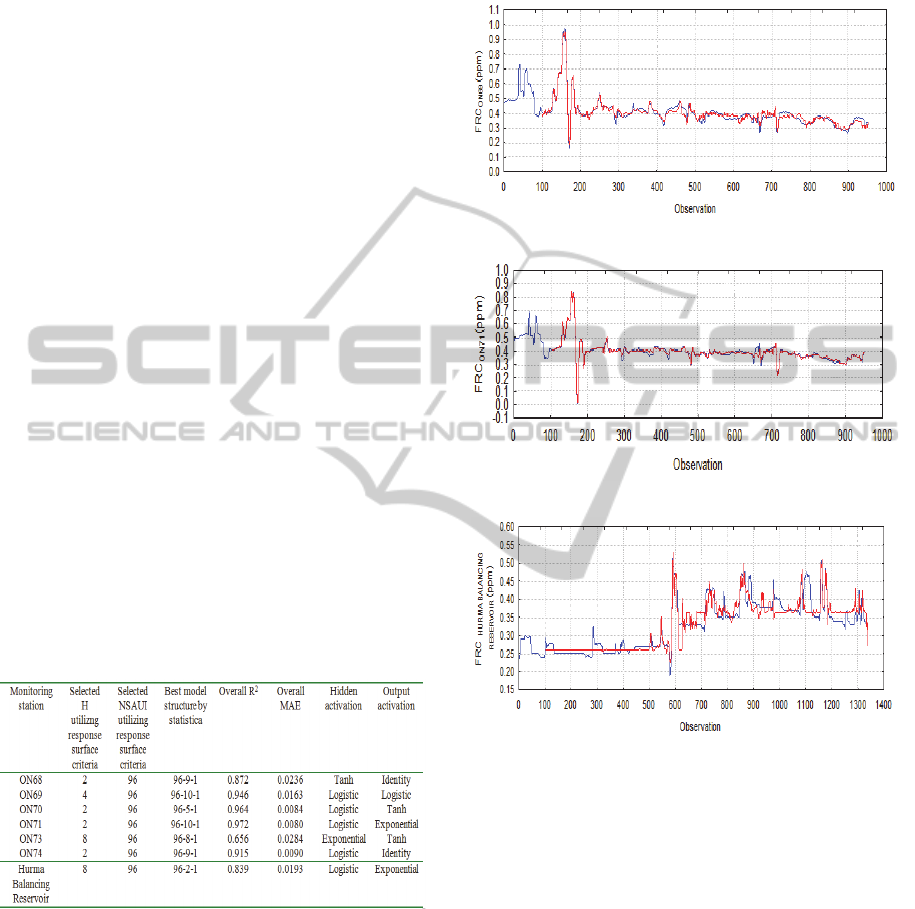
The best SISO-TS-ANN models for these

monitoring stations as suggested by response

surfaces are summarized in Table 1. For ON 69,

maximum attainable R

was very high (0.946) and

MAE value was less than 0.02 ppm (0.0163 ppm).

For ON 71, maximum attainable R

was even higher

(0.972) and the corresponding minimum MAE was

0.008 ppm. For Hurma balancing reservoir, the

attainable performance and precision levels were

also satisfactory with 0.839 and 0.0193 ppm values

of R

and MAE levels respectively.

Table 1: The performance levels of SISO-TS-ANN model

structures as suggested by R

and MAE response surfaces.

Figure 4 summarizes the model predictions and

measurements as comparative time series.

Note that one may not still observe the impact of

traveling time from the figured out results because

of dynamically changing complex nature of the

network under study. However, we can at least say

that as the distance from major source of chlorine

water supply increases, R

values decrease in a

nonlinear fashion and MAE values increase again in

non-linear fashion.

One of the major concerns was to establish

trends for precision and performance levels as a

function

of distance from major source of chlorine.

(a) Measured FRC (Blue) and MLP 96-10-1 Model (Red)

results for ON-69.

(b) Measured FRC (Blue) and MLP 96-10-1 Model (Red)

results for ON-71.

results for Hurma Balancing Reservoir.

Figure 4: SISO-TS-ANN model predictions and

measurements for ON69, ON71 and Hurma Balancing

Reservoir monitoring stations.

This was achieved by preparing non-linear plots of

maximum attainable R

and MAE as a function of

distance from chlorine feeding station, Bogacay

Pumping Station and Reservoir, see Figure 5.

4 CONCLUSIONS

Modelers prefer simple structures that give highest

precision and performance. This study has shown

that SISO-TSS-ANN models that have only single

input and single output can be efficiently utilized as

FRC forecasting tools in complex WDSs that are

IJCCI2012-InternationalJointConferenceonComputationalIntelligence

592

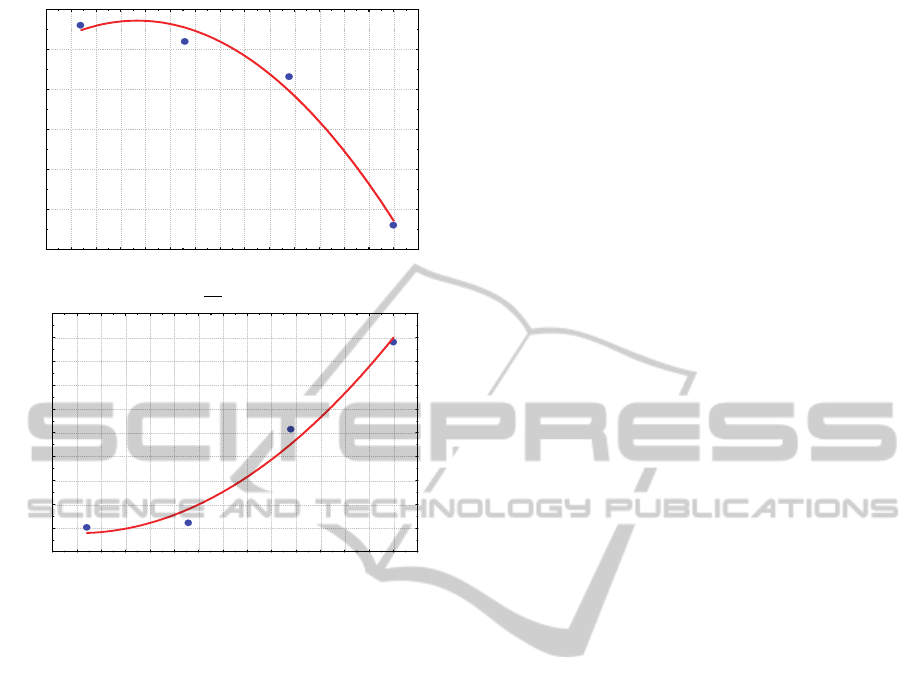
1.4 1.6 1.8 2.0 2.2 2.4 2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4

Distance from chlorine feeding location (km)

0.86

0.88

0.90

0.92

0.94

0.96

0.98

Maximu m a t t ain a b le R

(a)

1.41.61.82.02.22.42.62.83.03.23.43.63.84.04.24.4

Distance from chlorine feeding location (km)

0.006

0.008

0.010

0.012

0.014

0.016

0.018

0.020

0.022

0.024

0.026

Min imum at t a in a ble MAE(p pm)

(b)

Figure 5: Maximum attainable R

and minimum attainable

MAE as a function of distance from source of chlorine

supply.

supplied with raw waters of low FRC decay rates.

This may bring the possibility of reduction of

monitored variables in future that will create the

minimization of cost of monitoring. One of the

major conclusions is: irrespective of the locations of

the monitoring stations, utilization of maximum past

information for the single input has yielded best

results. We could not create any generalized rule for

the number of forecasting horizons that will yield

the best results. The number of forecasting horizons

should be specifically determined for each station by

examining its response surfaces. Therefore,

preparation of response surfaces for R

and MAE is

very useful in selecting best combinations of NSUAI

and H for developing forecasting tools.

REFERENCES

Bowden, G. J., Nixon, J. B., Dandy, G. C., Maier, H. R.,

Holmes, M., 2006. Forecasting chlorine residuals in a

water distribution system using a general regression

neural network. Mathematical and Computer

Modelling, 44, 469-484.

EPANET 2, 2000. Users’ Manual. Lewis A. Rossman,

Cincinnati, OH, USA.

Gibbs, M. S., Morgan, N., Maier, H. R., Dandy, G. C.,

Holmes, M., Nixon, J.B., 2003. Use of artificial neural

networks for modelling chlorine residuals in water

distribution systems. Modsim 2003 - International

Congress on Modelling and Simulation, Townsville.,

Australia, Part 2, 789-794.

May, R. J., Maier, H. R., Dandy, G. C., Nixon, J. B., 2004.

Control-oriented water quality modelling using

artificial neural networks. Proceedings on CD-ROM,

Enviro '04, Sydney, Australia.

May, R. J., Dandy, G. C., Maier, H. R., Nixon, J. B., 2008.

Application of partial mutual information variable

selection to ANN forecasting of water quality in water

distribution systems, Environmental Modelling and

Software 23, 1289–1299.

May, R. J., Maier, H. R., Dandy, G. C., Fernando,

T.M.K.G., 2008b. Non-linear variable selection for

artificial neural networks using partial mutual

information. Environmental Modelling and Software,

23, 1312-1326.

Polycarpou, M. M., Uber, J. G., Wang, Z., Shang, F.,

Brdys, M. A., 2002. Feed-back control of water

quality. In: IEEE Control Systems Magazine, pp. 68–

84.

Rodriguez, M. J., Sérodes, J. B., 1999. Assessing

empirical linear and non-linear modelling of residual

chlorine in urban drinking water systems.

Environmental Modelling and Software, 14, 93-102.

SANN (Statistica Automated Neural Network Software),

Stat Com, 2008.

Sharma, A., 2000. Seasonal to inter-annual rainfall

probabilistic forecasts for improved water supply

management: Part 1 – a strategy for system predictor

identification. Journal of Hydrology, 239 (1-4), 232 –

239.

Sérodes, J. B., Rodriguez, M. J., Ponton, A., 2001.

Chlorcast(c): a methodology for developing decision-

making tools for chlorine disinfection control.

Environmental Modelling and Software 16, 53-62.

Statsoft, 2012, Statistica Electronic Statistics Text book.

TUBITAK Proje Gelişme Raporu, 2009. İçme suyu

dağıtım sebekelerinde optimum klorlama

uygulamalarının matematiksel modeller kullan

ılarak

gerçekleştirilmesi ve dezenfeksiyon sistemlerinin

Yönetimi, Proje No:107G088, Antalya (Turkey) (In

Turkish).

SingleInputSingleOutputTimeSeriesArtificialNeuralNetworkModelsforFreeResidualChlorineForecastinginWater

DistributionNetworks

593