
A Methodological Proposal to Eliminate Ambiguities in the
Comparison of Vehicle Routing Problem Solving Techniques
Eneko Osaba and Roberto Carballedo
Deusto Institute of Technology, University of Deusto, Bilbao, Spain
Keywords: Vehicle Routing Problem, Combinatorial Optimization, Evolutionary Computing, Problem Bechmarks.
Abstract: In the field of vehicle routing problems it is very common to use benchmarks (sets of problem instances) to
evaluate new solving techniques or algorithms. The purpose of these benchmarks is to compare the
techniques based on the results or solutions obtained. Typically, the benchmarks include the values of
optimal solutions (if they have been obtained) or values of the best known solutions. In many cases, details
of how these results were obtained are not described. This may generate controversy and difficults the
comparisons of techniques. This paper shows an example of ambiguity in the results of an instance of the
most used VRPTW (Vehicle Routing Problem with Time Windows) bechmark. We show that when
analyzing the optimal solution and the best approximate solution of a specific problem, the two results are
equivalent. Finally, we will propose a set of guidelines to consider when publishing the results obtained by a
new algorithm.
1 INTRODUCTION
The heuristics and meta-heuristics for solving
combinatorial optimization problems have been and
still are recurrent topics in the research world. A lot
of new techniques or modifications of existing
techniques can be found in the literature every year.
The creation of new techniques can be aimed at
solving new problems adapted to real life. Another
objective may be the improvement of results of other
techniques which have appeared years ago.
Logically, each new method must be tested and
validated to determine its efficiency and
effectiveness, either in terms of results or the amount
of resources used (usually runtime). To check the
quality of a new technique, the best process is to
perform tests with benchmarks that can be found in
the literature. The benchmarks are composed of
instances of a particular problem, which researchers
can try to resolve to validate their new techniques.
Many of these instances have a known optimal
solution, so that can be known how good is an
algorithm by comparing its results with those offered
by the benchmarks. Taking into account this fact, it
is much easier to contrast the results obtained by the
own techniques compared with other techniques that
have used the same benchmarks. This way of
validating the algorithms is the correct way to
perform a reliable comparison between different
techniques.
For all these reasons, it can be seen the great
importance of testing benchmark in today's research.
A good proof of this is the large amount of authors
who use these banks to publish their results and
demonstrate the quality of their solutions. In the
field of vehicle routing problems can be found very
interesting benchmarks used by the scientific
community. For the Traveling Salesman Problem
(Lawler et al., 1985) for example, the library
TSPLIB (Reinelt, 1991) is the most widely used and
recognized. There have been many studies over
recent years that have used this library. On the other
hand, in relation to the Vehicle Routing Problem
with Time Windows (Condeau et al., 1999), the
Solomon’s VRPWT benchmark (Solomon, 2005) is
the most often used by researchers. These
benchmarks provide researchers a lot of problem
instances, offering for each instance the location of
the customers or places to visit, the maximum
number of vehicles, the capacity of the vehicles, the
demand of each customer, the service time, etc.
Moreover, in many cases, a collection of the best
results for each of the instances of the problems is
offered.
310
Osaba E. and Carballedo R..
A Methodological Proposal to Eliminate Ambiguities in the Comparison of Vehicle Routing Problem Solving Techniques.
DOI: 10.5220/0004171503100313
In Proceedings of the 4th International Joint Conference on Computational Intelligence (ECTA-2012), pages 310-313
ISBN: 978-989-8565-33-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
The aim of this paper is to show that sometimes,
the results provided as optimal solutions for these
benchmarks can be ambiguous, because it is not
clarified exactly the way in which these results were
obtained. This fact can make that the results shown
in scientific papers may not be completely accurate
and may create confusion among readers and
authors.
Specifically, with this article we want to
demonstrate the inaccuracy of the results presented
in the field of the vehicle routing problems, and
more specifically in the Solomon’s benchmark, in
which some results are presented as optimal, when,
actually, they are not. Apart from this
demonstration, we are going to propose some
guidelines for the presentation of results in order to
avoid confusions in the future. We believe that our
study may be helpful to facilitate the use of
benchmarks and avoid ambiguities.
2 DEMOSTRATION
To demonstrate the lack of accuracy in some
benchmarks and its results in the field of vehicle
routing problems, we will take as a reference the
VRPTW benchmark problems of Solomon
(Solomon, 2005). Specifically we will discuss the
ambiguity in the results presented for one of the
simplest problem instance of this benchmark: the
problem identified as C101. This instance has 100
cutomers (locations) whose distribution is clustered,
ie, customers are grouped geographically.
Furthermore, the time constraints of these customers
are quite flexible, which makes it relatively easy to
solve the problem and reach the optimal solution (in
terms of number of vehicles and total distance).
In the Solomon's benchmark web site (Solomon,
2005), we find that the best optimal solution for this
instance has a distance of 827.30 (Kohl et. al., 1999)
units (for instance kilometers). On the other hand,
we can find a value of 828.94 (Rochat and Taillard,
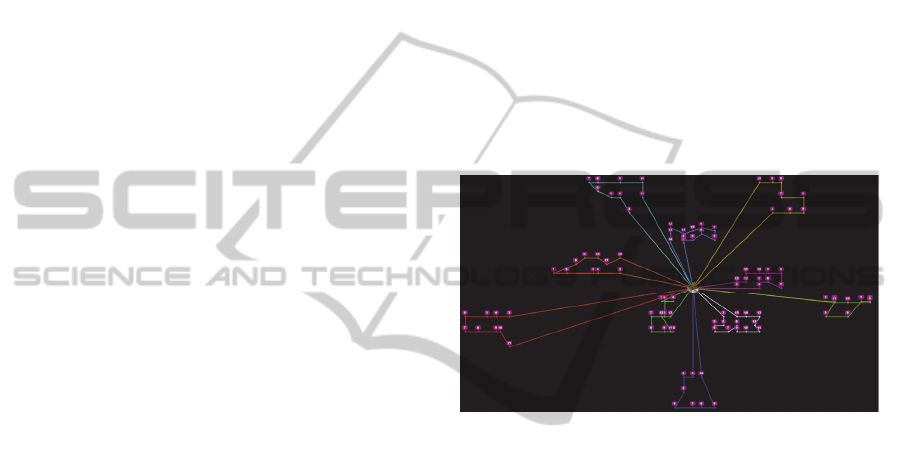
1995) for best result obtained using a heuristic
technique (figure 1 shows a graphical representation
of the routes).
In both solutions, the number of routes is 10 and
that number matches the number of clusters in which
customers are grouped. Finally, the difference in
absolute value between the two solutions is 1.64.
Apparently the two solutions are different. This
might suggest that to date, no heuristic technique has
obtained the optimal solution for this problem. But if
we analize the problem and solution techniques in
depth, it can be conclude that both solutions are the
same. Therefore both of the techniques obtain the
optimal solution (or rather, the best known solution).
The main difference between the two solutions is the
form in which each technique calculates distances
between two points. Both techniques use Euclidean
distances but one of them expresses the distance in
integer values (optimal technique), and the other in
decimal (heuristic technique). Indeed, the technique
that gets the best value converts the distances
between customers to work with integer values.
Firstly the distances between customers are
multiplied by 10 and the decimals are removed.
Then computes the solution to the problem, using
integer values for the Euclidean distances. And
finally, the result is divided by 10. As can be seen,
the justification that the solutions obtained by the
two techniques is different, is due to rounding.
Figure 1: graphical representation of the routes.
To be aware of the bug that causes rounding,
suppose that the distance between customer A and B
is 456.654. In this case, heuristic techniques use
456.654, while the optimal techniques use an integer
value of 4566. This results in the latter techniques
drag a small gap which ultimately is reflected in the
final solution.
To demonstrate that essentially the two solutions
are equivalent we show the results obtained by two-
solving techniques using the distance values with
and without rounding to integer values.
The first technique used, is a technique based on
the Solomon’s I1 initialization heuristic (Solomon
1987) with an improvement in the validation of time
windows known as time windows compatibility,
introduced by Joubert (Joubert, 2003). The
parameters of the I1 heuristic: α1, α2, μ and λ were
respectively: 0.2, 0.8, 0.0 and 0.2; and the criterion
for choosing the seed customer was: “the customer
with the earliest deathline schedule”.
The second technique used is a memetic
algorithm, which combines a genetic algorithm with
tabu search. The main characteristics of the genetic
algorithm are: the Very Greedy Crossover (Julstrom,
AMethodologicalProposaltoEliminateAmbiguitiesintheComparisonofVehicleRoutingProblemSolvingTechniques
311

1995) as crossover operator; the Exchange Mutation
(Banzhaf 1990) as mutation function; and finally the
selection criteria combines a 50% of the best
individuals and other 50% of individual selected at
random. For the Tabu algorithm the Vertex Insertion
successors function (Cordeau and Laporte, 2003)
with a strict tabu criterion is used. This criterion
implies that the tabu list stores the nodes of the last
movements. These nodes may not be the target of
another movement while the are on the tabu list. The
tabu list size is N/4, where N is the number of nodes
of the problem instance. The implementation of the
tabu search is performed on the children (created by
the genetic algorithm), after applying crossover and
mutation process, in order to optimize the new
chromosomes (or individuals).
The first technique is designed to VRPTW
problems, therefore, its application to the problem is
direct C101. In the case of meta-heuristic, which is
initially designed for TSP (Travelling Salesman
Problem), a conversion of the original problem has
been necessary. To do this, customers are grouped
geographically into 10 groups, and each group has
become a TSP problem. Furthermore, as discussed
above, the problems have been resolved with
distances in integer and decimal values. In relation
to the number of executions, in both cases we have
obtained the optimal solution with a single run.
Table 1 shows the results obtained. Each row
represents a path, and the final row shows the
accumulated values. The first column represents the
solution using integer values, and the second column
the solution using decimal values.
Table 1: Results, divided by routes.
Route Euclidean Dist. Integer Dist.
Route 1 646
64.807
Route 2 594
59.618
Route 3 593
59.403
Route 4 507
50.804
Route 5 759
76.070
Route 6 958
95.943
Route 7 1271
127.297
Route 8 970
97.227
Route 9 1017
101.883
Route 10 958
95.885
TOTAL 8273/10 = 837.3 828.936
These results show how the two techniques,
using different measures of distance, can find two
different solutions, when the solutions ares really the
same. In the appendix of this paper the composition
and the order of customers for each of the routes can
be found.
3 CONCLUSIONS
With this paper we have demonstrated the ambiguity
and confusion that can generate a lack of accuracy in
the benchmarks. This inaccuracy leads to the
existence of papers that ensures that the optimal
solution for the instance C101 of the Solomon
benchmark is 827.3 (Desrochers et al., 1992), while
other studies assure that the best solution is 828.94
(Lau, Sim and Teo, 2003). Apart from these, there
are papers which even mix both solutions, making
unreliable the results shown (Chen and Ting, 2005).
This is because they compare their solutions with
decimal distances, with solutions that have used
integer values.
With all this, we propose that the benchmarks
should have a greater level of detail, explaining what
pattern of distances has been used for each of the
solutions presented. Failing that, it would be a good
alternative the addition of a section which provides
the optimal solutions in its entirety, showing the
compositions of each of the routes and its distances,
as we do in this paper.
In case of problems with more than one objective
to minimize, it would be interesting to show the
optimization criteria used, and therefore, the
objective function.
Finally, another point that would improve the
quality of the benchmarks could be the generation of
an extra section to display the optimal execution
times, or just mention the time ranges in which the
execution of an algorithm could move to consider it
a good run time. All this, of course, subject to the
computer from which it is executed, a fact that
should also be taken into account. Details of the
issues to be taken into account when comparing
results obtained by different algorithms can be found
in the work presented by Bräysy and Gendreau
(Bräysy and Gendreau, 2005).
REFERENCES
Banzhaf, W., 1990. The “Molecular” Traveling Salesman.
Biological Cybernetics 64: 7–14.
Bräysy O. and Gendreau, M., 2005. Vehicle routing
problem with time windows, Part I: Route
construction and local search algorithms. INFORMS
Transportation Science, no. 39, pp. 104-118.
Chen, C. H., Ting, C. J., 2005. A hybrid ant colony system
for vehicle routing problem with time windows.
Journal of the Eastern Asia Society for Transportation
Studies, 6: 2822-2836.
Condeau, F., Desaulniers, G., Desrosiers, J., Solomon, M.,
Soumis, F., 1999. The VRP with time windows.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
312

Technical Report Cahiers du GERAD G-99-13, École
des Hautes Études Commerciales de Montréal.
Cordeau J. F., Laporte G., 2003. A tabu search heuristic
for the static multi-vehicle dial-a-ride problem.
Transportation Research Part B: Methodological, 37:
579-594.
Desrochers, M., Desrosiers, J., Solomon M. M., 1992. A
New Optimization Algorithm for the Vehicle Routing
Problem with Time Windows. Operations Research,
40: 342.354.
Joubert J. W., 2003. An initial heuristic for the vehicle
routing and scheduling problem. MEng thesis,
University of Pretoria, Pretoria.
Julstrom, B.A., 1995. Very greedy Crossover in a Genetic
Algorithm for the TSP. Proceedings of the 1995 ACM
symposium on applied computing: 324-328.
Kohl, N., Desrosiers, J., Madsen, O. B. G., Solomon, M.
M., and Soumis, F., 1999. 2-Path Cuts for the Vehicle
Routing Problem with Time Windows. Transportation
Science, Vol. 33 (1), 101-116.
Lau, H. C., Sim, M., Teo, K. M. 2003. Vehicle routing
problem with time windows and a limited number of
vehicles. European Journal of Operational Research,
148: 559-569.
Lawler, E. L., Lenstra, J. K., Rinnooy, K., Shmoys, D. B.,
1985. The traveling Salesman Problem: A guided tour
of combinatorial optimization. Willey – Interscience
Publication.
Reinelt, G., 1991. TSPLIB – A traveling salesman
problem library. ORSA Journal on Computing, 3: 376
– 384.
Rochat, Y. And Taillard, E. D. 1995 Probabilistic
Diversification and Intensification in Local Search for
Vehicle Routing. Journal of Heuristics 1, 147-167.
Solomon, M. M., 1987. Algorithms for the vehicle routing
and scheduling problems with time windows.
INFORMS Operations Research, 35: 254-265.
Solomon, M. M., 2005. VRPTW Bechmark Problems.
http://web.cba.neu.edu/~msolomon/problems.htm.
APPENDIX
Below are the routes of the solution to the C101
problem. In each route the sequence of customer
locations (X and Y) are shown. Note that the first
and last location of each route is exactly the same,
and corresponds to the central depot (which is a
requirement of VRPTW problems).
Route 1: [40, 50] [33, 35] [33, 32] [35, 32] [35, 30]
[32, 30] [30, 30] [30, 32] [28, 30] [25, 30] [26, 32]
[25, 35] [28, 35] [30 35] [40, 50]
Route 2: [40, 50] [42, 65] [42, 66] [40, 66] [38, 68]
[35, 66] [35, 69] [38, 70] [40, 69] [42, 68] [45, 70]
[45, 68] [45, 65] [40, 50]
Route 3: [40, 50] [45, 35] [47, 35] [45, 30] [48, 30]
[50, 30] [53, 30] [53, 35] [50, 35] [50, 40] [48, 40]
[47, 40] [40, 50]
Route 4: [40, 50] [30, 50] [25, 50] [25, 52] [23, 52]
[20, 50] [20, 55] [23, 55] [25, 55] [28, 55] [28, 52]
[30, 52] [40, 50]
Route 5: [40, 50] [60, 60] [63, 58] [65, 60] [68, 60]
[70, 58] [75, 55] [72, 55] [66, 55] [65, 55] [60, 55]
[40, 50]
Route 6: [40, 50] [58, 75] [60, 80] [62, 80] [65, 82]
[67, 85] [65, 85] [60, 85] [55, 85] [55, 80] [40, 50]
Route 7: [40, 50] [85, 25] [87, 30] [88, 30] [92, 30]
[95, 30] [95, 35] [90, 35] [88, 35] [85, 35] [40, 50]
Route 8: [40, 50] [10, 40] [8, 40] [10, 35] [5, 35]
[2, 40] [0, 40] [0, 45] [5, 45] [8, 45] [40, 50]
Route 9: [40, 50] [42, 15] [42, 10] [44, 5] [40, 5]
[38, 5] [35, 5] [38, 15] [40, 15] [40, 50]
Route 10: [40, 50] [22, 75] [20, 80] [25, 85] [22, 85]
[20, 85] [15, 80] [15, 75] [18, 75] [40, 50]
AMethodologicalProposaltoEliminateAmbiguitiesintheComparisonofVehicleRoutingProblemSolvingTechniques
313
